Перевод поста Стивена Вольфрама (Stephen Wolfram) "Solomon Golomb (1932–2016)".
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации

---

Содержание

— Наиболее часто используемый математический алгоритм в истории
— Как я встретил Сола Голомба
— История Соломона Голомба
— Регистры сдвига
— Предыстория регистров сдвига
— Для чего нужны последовательности, генерируемые регистрами сдвига?
— Ну и где же эти регистры?
— Клеточные автоматы и регистры сдвига с нелинейной обратной связью
— Полиомино
— Остальная часть истории

---

Наиболее часто используемый математический алгоритм в истории

Октиллион. Миллиард миллиардов миллиардов. Это очень приблизительная оценка того, сколько раз мобильный телефон или другое устройство сгенерировало бит с помощью регистра сдвига с линейной обратной связью максимальной длины. Думаю, это самый используемый математический алгоритм в истории. Автор — Соломон Голомб, скончавшийся 1 мая, с которым мы были знакомы больше 35 лет.

Основой книги Соломона Голомба «Последовательности регистрового сдвига», опубликованной в 1967 году, были его работы 1950-х гг. А ее содержание живет в каждой из современных систем связи. Прочтите спецификации для 3G, LTE, Wi-Fi, Bluetooth или даже для GPS, — и вы найдете упоминания о многочленах, определяющих последовательности, генерируемые регистрами сдвига, которые эти системы используют для кодирования отправляемых ими данных. Соломон Голомб — человек, который создал эти многочлены.

Кроме того, он играл важную роль в вычислении расстояния до Венеры с использованием радиолокатора, а также в разработке кодировки изображений для отправки с Марса. Он представил миру то, что назвал полиомино (которые позже вдохновили создателей Тетриса — «Tetromino tennis»). Он создал и решил бесчисленное количество математических головоломок и каламбуров. Лет 20 назад я узнал, что он был очень близок к открытию моего любимого правила 30 для клеточных автоматов еще в 1959 году, когда я только родился.

Как я встретил Сола Голомба

Почти всех ученых и математиков, с которыми я знаком, я узнал благодаря моим профессиональным связям. Но только не Сола Голомба. Шел 1981 год, и я, 21-летний физик (ставший немного известным в СМИ потому, что был самым молодым получателем премии МакАртура на первой церемонии награждения) занимался исследованиями в Калифорнийском технологическом институте. В дверь моего кабинета постучались, и вскоре его порог переступила молодая женщина. Уже это было необычно, потому что в те времена там, где занимались теоретической физикой высоких энергий, женщин было безнадежно мало. Хотя я и прожил в Калифорнии несколько лет, я, тем не менее, не покидал пределов университета, а потому оказался плохо подготовлен к всплеску южнокалифорнийской энергии, которая ворвалась ко мне в кабинет. Женщина представилась Астрид и сказала, что посещала Оксфорд и знала кого-то, с кем я был в детском саду. Она объяснила, что ей было поручено собрать сведения об интересных людях в районе Пасадены. Думаю, она считала меня трудным случаем, но, тем не менее, настаивала на разговоре. И однажды, когда я пытался рассказать что-то о том, чем я занимаюсь, она сказала: "Вы должны встретиться с моим отцом. Он уже пожилой человек, но его ум по-прежнему острый, как бритва". И так случилось, что Астрид Голомб, старшая дочь Сола Голомба, познакомила меня с ним.

Семья Голомб жила в доме, расположенном в горах близ Пасадены. У них было две дочери: Астрид — немного старше меня, честолюбивая голливудская девушка, и Беатрис — примерно моего возраста и научного склада ума. Сестры Голомб часто устраивали вечеринки — как правило, у себя дома. Темы были разные: это и вечеринка в саду и крокет с фламинго и ежами ("победителем станет тот, чей костюм более всего будет соответствовать заявленной теме"), или вечеринка в стиле Стоунхендж с инструкциями, написанными рунами. На этих вечеринках пересекались молодые и не очень люди, в том числе — различные местные светила. И на них, немного в стороне, присутствовал всегда маленький человек с большой бородой, немного похожий на эльфа и носивший всегда темное пальто, — сам Соломон Голомб.

Постепенно я узнал немного о нем. То, что он был вовлечен в "теорию информации". То, что он работал в Университете Южной Калифорнии. То, что у него были различные неопределенные, но, по-видимому, высокоуровневые правительственные и другие связи. Я слышал про регистры сдвига, но практически ничего не знал о них.

Осенью 1982 года я посетил Bell Labs в Нью-Джерси и выступил с докладом о моих последних результатах в области клеточных автоматов. Одной из тем, которые я обсуждал, были «аддитивные» (или «линейные»), клеточные автоматы, а также их поведение с ограниченным числом клеток. Всякий раз, когда клеточный автомат обладает ограниченным числом клеток, его поведение в конечном итоге неизбежно будет повторяться… Однако по мере увеличения размера максимальный период повторения, — скажем, для правила 90 для аддитивного клеточного автомата, — скачет как будто бы совершенно случайным образом: 1, 1, 3, 2, 7, 1, 7, 6, 31, 4, 63,… Однако за несколько дней до выступления я заметил, что эти периоды, кажется, следуют формуле, которая зависит от простых множителей или числа клеток. Но когда я упомянул об этом, кто-то из сидящих далеко поднял руку и спросил: «Не знаете ли вы, работает ли это для n = 37?" В своих экспериментах я не имел дела с этим числом, поэтому я не знал. Но почему кто-то спросил меня об этом?

Того, кто спросил меня, звали Эндрю Одлыжко — он был теоретиком из Bell Labs. Я спросил его: "Что же заставляет вас думать, что с n = 37 может быть связано что-то особенное?". "Ну," — сказал он, — "я думаю, что то, что вы делаете, связано с теорией регистров сдвига с линейной обратной связью", и он предположил, что я смотрел книгу Сола Голомба. "Ах, да," — сказал я, — "я знаю его дочерей...". Эндрю был прав: существует очень элегантная теория аддитивных клеточных автоматов на основе полиномов, аналогичная теории Сола, разработанной для регистров сдвига с линейной обратной связью. Эндрю и я написали неплохо теперь цитируемую статью об этом (это тот редкий случай, когда традиционные математические методы позволяют описать поведение клеточного автомата). А для меня побочным эффектом было то, что я узнал кое-что о том, чем же занимался Соломон Голомб (если вы помните, это все было до появления Интернета).

История Соломона Голомба

Соломон Голомб родился в Балтиморе, штат Мэриленд, в 1932 году. Его семья была родом из Литвы. Его дед был раввином, а отец еще совсем молодым переехал в США и получил степень магистра в области математики, после чего ушел в средневековую еврейскую философию и также стал раввином. Мать Сола происходила из известной русской семьи, изготавливавшей сапоги для царской армии, а затем руководила банком. Сол преуспевал в школе, будучи сильнейшим в дебатах. Воодушевленный отцом, он интересовался математикой и в 17 лет опубликовал статью о простых числах. После окончания средней школы он поступил в Университет Джона Хопкинса, чтобы изучать математику, и едва не попал в квоту на студентов-евреев (так что ему пришлось пообещать, что не уйдет в медицину, и затем Сол, увеличив себе нагрузку вдвое, окончил университет в 1951 году за половину обычного срока обучения).

Оттуда он отправился в Гарвард в аспирантуру по математике. Однако до этого он поработал летом в Glenn L. Martin Company — аэрокосмической компании, основанной в 1912 году, которая в 1920-е годы переехала в Балтимор из Лос-Анджелеса и стала оборонным подрядчиком, что в конечном итоге вылилось в Lockheed Martin. В Гарварде Сол специализировался на теории чисел, и, в частности, на вопросах характеризации множеств простых чисел. Но каждое лето он возвращался в Martin Company. Как он рассказывал позже, в Гарварде "вопрос о том, имело ли какое-либо практическое приложение то, чему там учили и учились, нельзя было даже произносить вслух, не говоря уже о его обсуждении". Но в Martin Company он обнаружил, что чистая математика, которую он знал, — даже простые числа, — действительно имеет практическое применение, в том числе и регистр сдвига.

В первое лето его работы на Martin Company Сол был закреплен за группой теории управления. Во второе лето он был помещен в группу по изучению связи. А в июне 1954 года случилось так, что его начальник побывал на конференции, где услышал о странном поведении сдвига регистра с линейной обратной связью, и он спросил Сола, сможет ли он заняться этими исследованиями. Вскоре Сол понял, что эту тему можно исследовать с помощью полиномов над конечными полями. Весь следующий год он делил свое время между аспирантурой в Гарварде и консалтингом для Martin Company, а в июне 1955 года он написал свой окончательный доклад — "Последовательности со случайными свойствами", который стал основополагающим для теории регистра сдвига.

Сол любил математические головоломки, и в процессе обдумывания головоломки с организацией костяшек домино на шахматной доске он изобрел то, что назвал впоследствии "полиомино". Он выступил с докладом о них в ноябре 1953 г. в Гарвардском математическом клубе, опубликовал о них статью (его первая исследовательская работа) и выиграл математическую премию Гарварда за работу с ними.



В июне 1955 года Сол уехал на год в Университет Осло на программу Fulbright Fellowship — отчасти для того, чтобы поработать с некоторыми выдающимися теоретиками, отчасти для того, чтобы выучить норвежский, шведский и датский языки (и изучить некоторые рунические рукописи) и пополнить свою коллекцию языковых навыков. За время своего пребывания в Осло он закончил длинную статью о простых числах и успел попутешествовать по Скандинавии, а в Дании встретил молодую женщину по имени Бо (Bodil Rygaard), — она была родом из большой семьи и родилась в сельской местности, известной только своим торфяным мхом, но умудрилась попасть в университет и изучала философию. Сол и Бо, судя по всему, поладили, и спустя несколько месяцев поженились.

Когда в июле 1956 г. они вернулись в США, Сол дал несколько интервью, а затем поступил на работу в JPL — лабораторию реактивного движения, которая отделилась от Калифорнийского технологического института и занималась военными разработками. Сол был включен в группу по коммуникациям в качестве старшего инженера-исследователя. Это было тогда же, когда люди из лаборатории были готовы запустить спутник. Однако правительство не позволяло им, опасаясь, что это будет выглядеть как военные действия. Все изменилось в октябре 1957 года, когда Советский Союз запустил свой спутник якобы в рамках Международного геофизического года. Удивительно, но США потребовалось всего 3 месяца для того, чтобы запустить Эксплорер-1. JPL много сделала для запуска спутника, и группу Сола (где у него работали технические специалисты над реализацией регистрового сдвига в электронном виде) бросили на создание детекторов радиации; во время этой работы Сол смог вернуться ненадолго в Гарвард, чтобы сдать итоговые экзамены на получение степени PhD.

Это было время сосредоточения сил вокруг JPL и космической программы. В мае 1958 года была сформирована новая группа обработки информации, которую возглавил Сол, и в том же месяце родился первый его ребенок — Астрид. Сол продолжил свое исследование последовательностей, генерируемых регистрами сдвига применительно к радиоуправлению ракетами, устойчивому к заклиниванию. В мае 1959 года появилась вторая дочь Сола, которую назвали Беатриче (хорошая последовательность: А, Б...). Осенью 1959 года Сол взял академический отпуск в MIT, где он познакомился с Клодом Шенноном и рядом других светил MIT и занимался теориями информации и алгебраических кодов.

На тот момент он уже проделал определенную работу по теории кодирования в области биологии. Несмотря на то, что цифровая природа ДНК была обнаружена Джимом Уотсоном и Фрэнсисом Криком еще в 1953 году, до сих пор не было ясно, как именно последовательности из четырех возможных пар оснований кодируют 20 аминокислот. В 1956 году Макс Дельбрюк — бывший советник Уотсона на постдоке в Калифорнийском Технологическом — консультировался по этому вопросу с сотрудниками Лаборатории реактивного движения. Сол и двое его коллег проанализировали идею Фрэнсиса Крика и придумали «коды без запятых», в которых перекрывающиеся тройки пар оснований могут кодировать аминокислоты. Анализ показал, что таким образом могут быть закодированы ровно 20 аминокислот. Это было одно из самых удивительных объяснений; но, к сожалению, биология на самом деле работает не так (в биологии используется более простое кодирование, при котором некоторые из 64 возможных троек ничего не представляют).

Помимо биологии Сол также занимался физикой. Его последовательности, генерируемые регистрами сдвига, пригодились для вычисления дальности с помощью радара (используется в GPS); также Сол был назначен ответственным за то, чтобы найти расстояние до Венеры. И так получилось, что в начале 1961 года, когда Солнце, Венера и Земля выстроились наиболее удачно, Сол с помощью 85-футовой радиоантенны Голдстоун, расположенной в пустыне Мохаве, получил радиолокационный сигнал от Венеры и уточнил имеющиеся у нас данные о расстояниях Земля-Венера и Земля-Солнце.

Учитывая интерес Сола к языкам, кодированию и космосу, неудивительно, что он заинтересовался инопланетянами. В 1961 году он написал статью для ВВС под названием "Краткое пособие по внеземной лингвистике", и в течение следующих нескольких лет написал несколько статей по этой теме для более широкой аудитории. Он сказал: «в отношении контакта с инопланетянами существует 2 основные проблемы: одна из них — проблема обнаружения взаимоприемлемого канала. Другая — более философская проблема (семантическая, этическая и метафизическая), состоящая в поиске надлежащего предмета для дискуссии. Проще говоря, сначала нам требуется найти общий язык, а потом мы должны подумать, что сказать». Далее он со свойственным ему юмором продолжал: "Естественно, мы не должны рассказывать им слишком много, пока не узнаем, достаточно ли благородные у них намерения. Правительство, несомненно, создаст Космическое Разведывательное Управление (КРУ) для мониторинга внеземного разума. Будут приняты экстремальные меры безопасности. Как однажды отметил Герберт Уэллс [или это был эпизод из Сумеречной зоны?], что, даже если инопланетяне скажут нам со всей откровенностью, что их единственная цель — «служить человечеству», мы должны выяснить, желают ли они послужить нам в запеченном или в жареном виде."

Во время своей работы в лаборатории JPL Сол также преподавал в близлежащих университетах: Калифорнийском технологическом институте, Университете Южной Калифорнии и в университете Лос-Анджелеса. Осенью 1962 года, после изменения ситуации в лаборатории (и, возможно, потому, что он хотел проводить больше времени со своими маленькими детьми), он решил стать профессором на полный рабочий день. Он получил предложения от всех трех университетов. Он хотел пойти туда, где он мог бы работать свободно. Ему сказали, что в Калифорнийском технологическом институте "никто кроме Нобелевских лауреатов не имеет никакого влияния", а в Лос-Анджелесе "такая бюрократия, что никто и ни на что не может повлиять". В результате Сол выбрал университет Южной Калифорнии даже несмотря на его низкую репутацию. Весной 1963 года он приступил к работе в качестве профессора электротехники в конечном итоге проработал там 53 года.

Регистры сдвига

Прежде чем продолжить рассказ о жизни Сола, я должен объяснить, что такое регистр сдвига с линейной обратной связью (LFSR). Основная идея довольно проста. Представьте себе ряд квадратов, каждый из которых содержит 1 или 0 (скажем, черный или белый). В чистом регистре сдвига все происходящее сводится к смещению всех значений на один шаг влево, при этом крайнее левое значение теряется, а новое значение берется справа. Идея регистра сдвига с обратной связью заключается в том, что значение, которое сдвинулось, определяется (или «подается обратно») в зависимости от значений других положений в регистре сдвига. В регистре линейного сдвига с обратной связью значения из «ответвлений» в определенных позициях в регистре объединяются по модулю 2 (так что 1?1 = 0 вместо 2), или применяется XOR ("исключающее или").



Вот что происходит через некоторое время:



Как вы видите, регистр сдвига всегда сдвигает биты влево, а другие биты добавляются справа согласно простому правилу. Последовательность битов кажется случайной, хотя, как показано на рисунке, она в конечном итоге повторяется. Сол Голомб нашел элегантный математический способ анализа таких последовательностей и того, как они повторяются.

Если регистр сдвига имеет размер n, то у него есть 2ⁿ возможных состояний (соответствующих всем возможным последовательностям 0 и 1 при длине n). Поскольку правила для регистра сдвига детерминированы, любое данное положение должно всегда прийти к другому такому же положению. А это означает, что максимально возможное число шагов, которое регистр сдвига может пройти, прежде чем шаги начнут повторяться, равно 2ⁿ (на самом деле 2ⁿ — 1, так как положение со всеми 0 не может эволюционировать во что-нибудь еще).

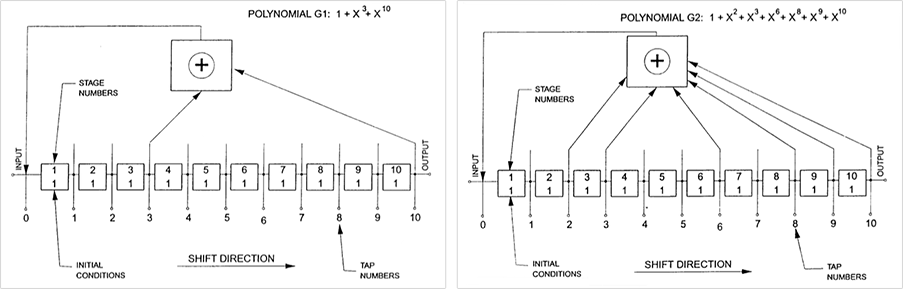
В приведенном выше примере, регистр сдвига имеет размер 7 и повторится ровно через 2⁷ — 1 = 127 шагов. Но какие регистры сдвига — с какими расположениями ответвлений — будут производить последовательности максимальной длины? Это вопрос Соломон Голомб начал исследовать летом 1954 года. И его ответ был прост и элегантен.

Регистр сдвига приведенный выше имеет ответвления в положениях 7, 6 и 1. Сол представил это алгебраически, используя многочлен х⁷ + х⁶ + 1. Он показал тогда, что генерируемая последовательность будет максимальной длины, если этот многочлен "неприводим по модулю 2"; поэтому он не может быть факторизован, что делает его аналогом простого числа среди многочленов; а наличие некоторых других свойств делает его "примитивным многочленом". На сегодняшний день это легко проверить с помощью системы Mathematica и языка Wolfram Language:



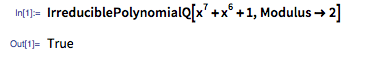
Тогда, в 1954 году, Сол должен был делать всё это вручную; он составил довольно длинную таблицу примитивных многочленов, соответствующих регистрам сдвига, которые выдавали последовательности максимальной длины:

Предыстория регистров сдвига

Идея поддержания оперативной памяти посредством "линий задержки", которые передают цифровые импульсы, восходит к началу эпохи ЭВМ. К концу 1940-х годов такие линии задержки применялись в цифровом виде с помощью ряда вакуумных трубок и назывались "регистры сдвига". Пока не ясно, когда были созданы первые регистры сдвига с обратной связью. Возможно, это было в конце 1940-х годов. Однако это событие до сих пор окутано тайной, потому что впервые они были использованы в военной криптографии.

Основная идея криптографии — изменение осмысленных сообщений таким образом, чтобы их нельзя было распознать; при этом, если вы знаете ключ, вы сможете воссоздать зашифрованное сообщение. Так называемые потоковые шифры работают по принципу создания длинных последовательностей как бы случайных элементов, и декодируются с помощью приемника, самостоятельно генерирующего ту же последовательность элементов.

Регистры сдвига с линейной обратной связью ценились в криптографии из-за длинных периодов повтора. Однако математический анализ, который Сол использовал, чтобы найти эти периоды, дает понять, что такие регистры сдвига не годятся для безопасной криптографии. Однако в начале они казались неплохими (особенно в сравнении с последовательными положениями ротора в Энигме); ходили упорные слухи, что на этой основе строились советские военные криптосистемы.

Еще в 2001 году, когда я работал над историческими заметками для моей книги Новый вид науки, мы с Солом долго говорили по телефону о сдвигах регистра. Сол сказал мне, что, когда он начинал, он ничего не знал о криптографической работе по регистрам сдвига. Он сказал, что сотрудники лаборатории Белла, лаборатории Линкольна и Лаборатории реактивного движения начали работать над регистрами сдвига примерно в то же время, что и он; однако ему удалось продвинуться немного дальше, что он и отметил в своем отчете от 1955 года.

В течение последующих лет Сол постепенно узнавал о различных предшественниках своих работ из литературы, посвященной чистой математике. Уже в 1202 году Фибоначчи говорил о том, что теперь называют числами Фибоначчи и которые генерируются рекуррентным соотношением (которое может рассматриваться как аналог регистра сдвига с линейной обратной связью, работающего с произвольными целыми числами, а не с нулями и единицами). Существуют также небольшие работы начала 1900-х по цикличности 0 и 1, однако первым крупномасштабным исследованием стала работа Ойстена Оре из Университета Осло. У Оре был студент по имени Маршалл Холл, который консультировал предшественника Агентства национальной безопасности в конце 1940-х гг. — вероятно, по теме регистров сдвига. Однако все, что он делал, было засекречено, и поэтому он договорился с Солом, чтобы тот опубликовал историю регистров сдвига с линейной обратной связью; Сол посвятил свою книгу Маршаллу Холлу.

Для чего нужны последовательности, генерируемые регистрами сдвига?

Я много раз замечал, что системы, определяемые простыми правилами, в конечном итоге имеют много вариантов приложений; регистры сдвига также следуют этой закономерности. И современное оборудование, и программное обеспечение напичкано регистрами сдвига: в обычном мобильном телефоне, вероятно, их десяток или два, реализованных, как правило, на аппаратном уровне, а иногда — и в программном обеспечении (когда я пишу здесь «регистр сдвига», я имею в виду регистр сдвига с линейной обратной связью — LFSR).

В большинстве случаев используются те регистры сдвига, которые дают последовательности максимальной длины (иначе известные как "М-последовательности"). Причины, по которым они используются, как правило, связаны с некоторыми их свойствами, которые обнаружил Сол. Они всегда содержат одинаковое количество 0 и 1 (хотя на самом деле всегда есть ровно одна дополнительная 1). Впоследствии Сол показал, что им также свойственно одинаковое количество последовательностей 00, 01, 10 и 11 — и для больших блоков тоже. Это свойство "баланса" это само по себе уже очень полезно, — к примеру, если тестировать все возможные комбинации битов в качестве входных данных.

Однако Сол обнаружил еще одно, даже более важное свойство. Замените каждый 0 в последовательности на 1, затем умножьте каждый элемент в сдвинутой версии последовательности на соответствующий элемент оригинала. Сол показал, что при сложении эти элементы всегда будут равны нулю (кроме случаев, когда никакого сдвига нет вообще). То есть последовательность не имеет никакой корреляции со сдвинутыми версиями самой себя.

Эти свойства будут верны для любой достаточно длинной случайной последовательности из 0 и 1. Удивительно, что для последовательностей максимальной длины эти свойства всегда верны. Последовательности имеют некоторые черты хаотичности, однако на самом деле они вовсе не хаотичны: они имеют вполне определенную, организованную структуру.

Именно эта структура, свойственная регистрам сдвига с линейной обратной связью, делает их непригодными для серьезной криптографии. Но они прекрасно подходят для базовой «перестановки элементов» и дешевой криптографии и активно используются для этих целей. Часто стоит задача просто «отбелить» сигнал (как в «белом шуме»). Иногда нужно передавать данные с длинными последовательностями 0. Но электроника в таком случае может запутаться, если «молчание» будет слишком долгим. Можно избежать этой проблемы через скремблинг исходных данных путем объединения его с последовательностью, генерируемую регистром сдвига. Именно это было сделано с Wi-Fi, Bluetooth, USB, цифровым TV, интернетом и т. д.

Побочный эффект скремблинга регистра сдвига — более сложное декодирование, что используется иногда для повышения безопасности (в технологии DVD для кодирования данных используется комбинация регистров сдвига с длиной 16 и 24 бита; многие GSM телефоны используют комбинацию из трех регистров сдвига для кодирования всех сигналов).

В GPS также используются последовательности регистра сдвига. Каждый GPS спутник непрерывно передает последовательность, генерируемую регистром сдвига, длиной 10 бит. По полученной части последовательности приемник может точно определить, в какое время принятый им сигнал был отправлен с конкретного спутника. И затем, путем сравнения задержки времени от различных спутников, приемник может триангулировать свое положение (существует также режим GPS, использующий регистр сдвига длиной 1024 бита).



Совершенно по-другому регистры сдвига используются для обнаружения ошибок. Скажем, некто передает блоки битов, и для каждого из них существует небольшая вероятность ошибки. Простой способ проверить единичную ошибку — включить "бит четности", который сообщает, какое количество 1 (нечетное или четное количество) должно быть в блоке битов. Можно также применять CRC (циклические проверки избыточности), которые могут искать большее количество ошибок, и вычисляются они путем подачи данных в регистр сдвига с линейной обратной связью. Есть также коды коррекции ошибок, которые позволяют не только обнаружить, но и исправить определенное количество ошибок, и некоторые из них также могут быть вычислены посредством последовательностей, генерируемых регистрами сдвига — и Сол Голомб использовал версии этих кодов, называемых коды Рида-Соломона, для кодирования видео для космического корабля на Марс.

Сфера применения последовательностей, генерируемых регистрами сдвига, становится все шире. Существует довольно экзотический пример использования последовательностей, генерируемых регистрами сдвига, к фазовому дрожанию часов в компьютере — разложение частоты, на которой процессор потенциально может генерировать радиочастотные помехи (выберите «Enable Spread Spectrum» в BIOS).

Одно самых известных применений последовательностей регистра сдвига — CDMA телефоны (множественный доступ с кодовым разделением). Сотовые телефоны получили свое название потому, что они работают в «клетках», и все телефоны определенной клетки соединены с определенной башней. Но как различные мобильные телефоны в «клетке» не мешают друг другу? В первых системах каждый телефон просто «согласовывал» с башней использование несколько иной частоты. Позже стали использовать различные срезы времени ( TDMA — множественный доступ с разделением каналов по времени). А CDMA в качестве разумной альтернативы использует последовательности регистра сдвига максимальной длины.

Идея заключается в том, чтобы все телефоны работали на одной и той же частоте, но каждый телефон кодировал свой сигнал, используя (в простейшем случае) разные варианты последовательностей, генерируемых регистрами сдвига. Согласно результатам Сола, разные варианты сдвига не коррелируют между собой, а потому сигналы мобильных телефонов не интерферируют. Так работает большинство сетей 3G.

Сол создал математическую основу для всего этого, а также перезнакомил друг с другом ряд ключевых фигур. Еще в 1959 году он познакомился с Ирвином Джейкобсом, который недавно получил докторскую степень в Массачусетском технологическом институте. Также он был знаком с Энди Витерби, который работал в Лаборатории реактивного движения. Сол познакомил их, и в 1968 году они основали компанию под названием Linkabit, работавшую над системами кодирования (в основном для военных целей).

В 1985 году Джейкобс и Витерби основали еще одну компанию под названием Qualcomm. Сначала дела у них шли не особенно хорошо, но к началу 1990-х годов, когда они начали производить компоненты для развертывания CDMA в сотовых телефонах, компания начала стремительно расти.

Ну и где же эти регистры?

Удивительно, что большинство людей никогда не слышали о регистрах сдвига и при этом взаимодействуют с ними всякий раз, когда пользуются современными системами связи, вычислительной техникой и т. д. Здесь несложно запутаться, учитывая, что за разными названиями и аббревиатурами оказываются те же последовательности регистров сдвига с линейной обратной связью (PN, псевдошум, M-, FSR, LFSR последовательности, MLS, SRS, PRBS, и т. д.).

Если рассматривать мобильные телефоны, то использование в них последовательностей, генерируемых регистрами сдвига, менялось на протяжении многих лет, — то увеличиваясь, то уменьшаясь. 2G сети основаны на TDMA, так что для кодирования своих данных не используют последовательности, генерируемые регистрами сдвига, однако до сих пор часто используют CRC (циклический избыточный код) для проверки блоков данных. 3G сети — крупнейшие пользователи CDMA, так что последовательности, генерируемые регистрами сдвига, задействованы в передаче каждого бита. 4G сети обычно используют сочетание времени и частоты слотов, не включающих последовательности регистров сдвига, хотя CRC еще используются: например, чтобы взаимодействовать с целостными данными, когда частотные окна перекрывают друг друга. 5G имеет более сложную структуру — с множеством антенн, динамически адаптирующихся для использования оптимального времени и частоты слотов. Однако половина их каналов, как правило, выделяется для «пилот-сигналов», которые используются для выведения локальной радиосреды; в их основе также лежат последовательности, генерируемые регистрами сдвига.

При производстве электроники обычно стараются достичь наиболее высокой скорости передачи данных при минимальных энергозатратах, позволяющих битам преодолевать шумовой порог. И, как правило, этот путь приводит к автоматизации обнаружения ошибок, — а значит, к использованию CRC (циклического избыточного кода) и, следовательно, последовательностей, генерируемых сдвиговым регистром. Это касается практически всех видов шин внутри компьютера (PCIe, SATA и т. д.): обеспечивающих взаимодействие частей центрального процессора, или получение данных с устройств, или подключение к дисплею с HDMI. В случае с дисками или с памятью CRC и другие коды, основанные на последовательностях, генерируемых регистрами сдвига, также практически повсеместно используются для работы на максимальной скорости.

Регистры сдвига настолько вездесущи, что практически невозможно оценить, сколько бит ими генерируется. Существует примерно 10 миллиардов компьютеров, чуть меньше — телефонов, и огромное количество устройств во встроенным IoT («интернетом вещей»). Почти у каждого автомобиля в мире (а их больше миллиарда!) — около 10 встроенных микропроцессоров.

На какой частоте работают регистры сдвига? В системах связи есть базовая несущая частота в герцовом диапазоне, а также «скорость передачи элементов сигнала», которая говорит о том, как быстро осуществляется множественный доступ (речь идет о CDMA) в диапазоне МГц. С другой стороны, в шинах внутри компьютеров все данные передаются с помощью регистров сдвига — с наилучшей скоростью передачи в герцовом диапазоне.

Существует по крайней мере 10 миллиардов линий связи, работающих по крайней мере 1/10 миллиарда секунд (около 3-х лет), которые используют по меньшей мере 1 миллиард битов из сдвиговых регистров каждую секунду, что означает, что на сегодняшний день алгоритм Сола был использован по крайней мере октиллион раз.

Действительно ли этот алгоритм используется наиболее часто? Думаю, да. Я подозреваю, что конкуренцию могут составить только арифметические операции. В наши дни процессоры способны проводить триллион арифметических операций в секунду, и такие операции необходимы для почти каждого бита, генерируемого с помощью компьютера. Но как выполняется арифметика? На каком-то уровне это просто реализация цифровой электроники.

Однако есть «алгоритмические идеи», которые остаются непонятными для всех, кроме дизайнеров микропроцессоров. Когда Бэббидж делал свою разностную машину (см. статью на Хабре "Распутывая историю Ады Лавлейс (первого программиста в истории)"), переносы стали большой помехой в выполнении арифметических операций (на самом деле, о регистре сдвига с линейной обратной связью можно думать как о системе, которая делает что-то вроде арифметических вычислений, но не осуществляет перенос). Существуют «деревья распространения сигнала переноса», оптимизирующие перенос. Есть также маленькие хитрости (вроде "алгоритма Бута", " деревьев Уоллеса" и т. д.), которые уменьшают количество битовых операций, необходимых для создания «внутренностей» арифметики. Но, в отличие от регистров сдвига с линейной обратной связью, единой алгоритмической идеи, которая использовалась бы практически где угодно, просто не существует; поэтому я думаю, что максимально длинные последовательности, генерируемые регистрами сдвига с линейной обратной связью, все-таки побеждают среди наиболее используемых последовательностей.

Клеточные автоматы и регистры сдвига с нелинейной обратной связью

Хотя на первый взгляд это и не кажется очевидным, оказывается, существует тесная связь между регистрами сдвига с обратной связью и клеточными автоматами, которые я много лет изучал. Базовая организация для регистра сдвига с обратной связью предусматривает вычисление за один раз одного бита. В клеточном автомате имеется одна линия клеток, и на каждом шаге все клетки обновляются параллельно, основываясь на правиле, которое зависит, к примеру, от значений их ближайших соседей.

Чтобы увидеть, как они связаны между собой, нужно запустить регистр сдвига с обратной связью размера n, и при этом отображать его состояние только каждые n шагов; другими словами, дать всем битам перезаписаться до повторного их появления. Если отображается каждый шаг регистра сдвига с линейной обратной связью (здесь — с двумя ответвлениями), то на каждом из шагов все сместится влево — и все. Но если сделать сжатую картинку, показывая только каждые n шагов, станет видна закономерность.



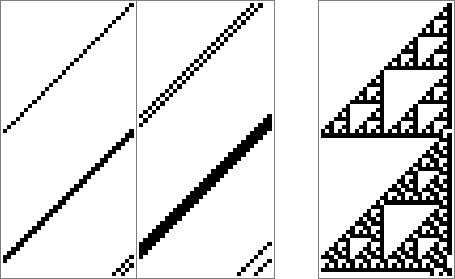
Это вложенный паттерн; и эта картина очень похожа на ту, которую можно получить в случае, если клеточный автомат возьмет клетку и соседнюю с ней и сложит их по модулю 2 (XOR). Вот что происходит с клеточным автоматом, если он располагает свои клетки так, что они находятся в окружности того же размера, что и регистр сдвига выше:



Вначале клеточные автоматы и паттерны сдвигового регистра оказываются точно такими же. Если посмотреть на эти картинки, становится менее удивительно, что математика регистров сдвига должна иметь отношение к клеточным автоматам. И, учитывая повторяемость вложенных паттернов, становится ясно, почему должна существовать элегантная математическая теория регистров сдвига.

Для типичных регистров сдвига, используемых на практике, не свойственны такие явно повторяющиеся паттерны. Вот несколько примеров регистров сдвига, которые генерируют последовательности максимальной длины. Факт в том, что ответвления находятся далеко друг от друга, что затрудняет нахождение визуальных следов вложенности.



Насколько же широко соответствие между регистрами сдвига и клеточными автоматами? Для клеточных автоматов правила генерации новых значений ячеек могут быть какими угодно. В регистрах сдвига с линейной обратной связью они всегда должны быть основаны на сложении по модулю 2 (или XOR). Это то, что означает «линейная» часть «регистра сдвига с линейной обратной связью». Также возможно использование любого правила для объединения значений для регистров сдвига с нелинейной обратной связью (NFSR).

И в самом деле: когда Сол разработал свою теорию для регистров сдвига с линейной обратной связью, он начал с нелинейного случая. Когда он прибыл в JPL в 1956 году, он получил лабораторию, укомплектованную стойками для маленьких электронных модулей. Сол рассказывал, что модули (каждый из которых был размером с сигаретную пачку) были построены для проекта Bell Labs для выполнения определенной логической операции (AND, OR, NOT, ...). Модули могут быть использованы вместе для реализации любых желаемых регистров сдвига с нелинейной обратной связью, обеспечивая около миллиона бит в секунду (Сол сказал мне, что кто-то пытался сделать то же самое с помощью универсального компьютера, и то, что заняло 1 секунду при использовании аппаратных модулей, потребовало 6 недель работы на универсальном компьютере).

Когда Сол стал изучать регистры сдвига с линейной обратной связью, первым его серьезным открытием стали периоды их повторения. И в случае с нелинейными он большую часть своих усилий направил на попытки понять то же самое. Он собрал все виды экспериментальных данных. Он рассказал мне, что он проверял даже последовательности длиной 2⁴⁵, что потребовало год. Он сделал резюме, как на картинке ниже (обратите внимание на визуализацию последовательностей, показанных на линии осциллограммы). Но ему так и не удалось придумать какой-то общей теории, какая была у него для регистров сдвига с линейной обратной связью.


 
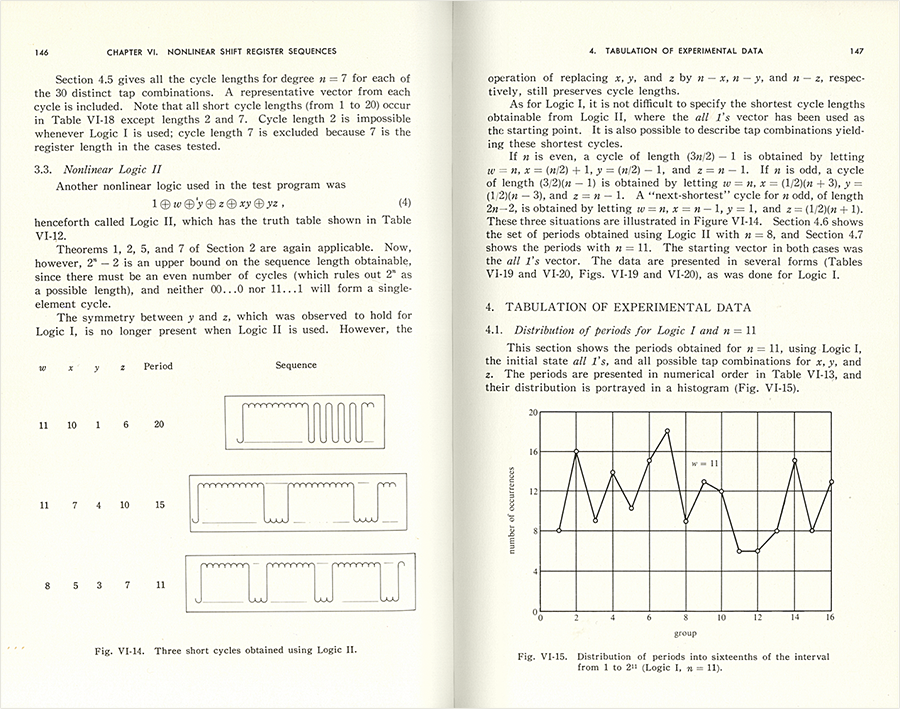
Неудивительно, что он не смог этого сделать. Уже в 1950-е годы появились теоретические результаты (в большинстве случаев основанные на идеях универсальных вычислений Тьюринга), того, какие программы в принципе могли бы сделать это. Я не думаю, что Сол или кто-либо еще когда-нибудь думал, что в регистрах сдвига с нелинейной обратной связью будут применяться очень простые (нелинейные) функции.

И только позже стало ясно, насколько сложным может быть поведение даже очень простых программ. Мой любимый пример — правило 30 для клеточного автомата, в котором значения соседних ячеек объединяются с помощью функции, которая может быть представлена в виде р + q + r + q*r mod 2 (или р XOR (q OR r)). Невероятно, но Сол рассматривал регистры сдвига с нелинейной обратной связью, основанные на аналогичные функциях: р + г + s + q*r + q*s + r*s mod 2. Вот здесь, ниже, — иллюстрации того, как функция Сола (которую можно рассматривать как "правило 29070"), правило 30 и несколько других подобных правил выглядят в регистре сдвига:



А здесь они, не ограниченные регистром фиксированного размера, похожи на клеточные автоматы:



Конечно, Сол никогда не делал картинок вроде этой (да и это было почти нереально сделать в 1950-е годы). Вместо этого он сосредоточился на периоде повторения как своего рода совокупной характеристике.

Сол задавался вопросом о том, могут ли регистры сдвига с нелинейной обратной связью быть источниками хаотичности. Из того, что на сегодняшний день известно о клеточных автоматах, ясно, что могут. К примеру, для создания хаотичности для системы Mathematica мы в течение 25 лет использовали правило 30 клеточных автоматов (хотя недавно мы отказались от него в пользу более эффективного правила, которое мы нашли, изучив триллионы возможностей).

О шифровании Сол говорил немного; хотя я думаю, что он недолго работал на правительство. Он сказал мне, что, хотя в 1959 году он и обнаружил "многомерные корреляционные атаки на нелинейные последовательности", в то же время он "тщательно избегал утверждений, что программа была для криптоанализа". Дело в том, что правило 30 для клеточных автоматов (и, возможно, также регистры сдвига с нелинейной обратной связью) могут быть хорошими криптосистемами — хотя из-за того, что они как будто эквивалентны регистрам сдвига с линейной обратной связью (а это не так), они никогда не использовались настолько, насколько можно.

Будучи энтузиастом, в течение последних нескольких десятилетий я пытался изучить всех предшественников моей работы над одномерными клеточными автоматами. Двумерные клеточные автоматы были немного изучены, а вот в случае с одномерными нашлась только одна чисто теоретическая работа. Я думаю, что из всего, что я видел, регистры сдвига с нелинейной обратной связью Соломона Голомба оказались ближе всего к тому, чем я в конечном итоге занялся четверть века спустя.

Полиомино

Услышав фамилию "Голомб", многие вспомнят о регистрах сдвига. Однако большинство вспомнит про полиомино. Сол не изобретал полиомино, хотя и придумал это название. Он сделал систематическим то, что раньше появлялось только в отдельных головоломках.

Главный вопрос, в ответе на который Сол был заинтересован, это как наборы полиомино могут быть организованы, покрыв некоторую область. Иногда это довольно очевидно, а иногда — довольно сложно. Свою первую статью о полиомино Сол опубликовал в 1954 году, однако действительно популярным сделал полиомино Мартин Гарднер в 1957 году (он вел колонку о математических играх в журнале Scientific American). Как пояснил Сол в предисловии к своей книге от 1964 года, в результате он получил "постоянный поток корреспондентов со всего мира и из всех слоев общества: председателей совета директоров ведущих университетов, жителей неизвестных монастырей, заключенных из известных тюрем...".

Игровые компании также обратили внимание на новые головоломки, и в течение нескольких месяцев появились заголовки вроде "новые сенсационные головоломки", а за ними последовали десятилетия других головоломок и игр на основе полиомино (нет, зловещий лысый парень не похож на Сола):









Сол печатал статьи о полиомино на протяжении еще 50 лет после первой публикации. В 1961 году он представил варианты деления на мелкие части "rep-tiles", с помощью которых можно создавать фрактальные («Infin-tile») узоры. Но почти все, что Сол делал с полиомино, включало в себя решение конкретных проблем.

Меня мало интересует специфика полиомино; меня интересуют связанные с ними феномены более общего характера. Кажется, что решить, можно ли с помощью нескольких простых форм «замостить» всю плоскость, легко. Но в случае с полиомино (а также со всеми играми и головоломками, основанными на них) становится ясно, что все не так-то просто. И действительно — в 1960-е годы было доказано, что эта задача теоретически неразрешима.

Если нас интересует только ограниченная область, то, в принципе, можно просто перечислить все мыслимые расположения фигур, а затем посмотреть, располагаются ли они так, как надо. Однако если нас интересует бесконечность, то этого можно не делать. Может быть, кто-то и найдет вариант удачного размещения миллиона фигур, но нет никакой гарантии, что этот результат может быть распространен дальше.

Оказывается, это может выглядеть как работающая машина Тьюринга — или клеточный автомат. Вы начинаете с линии плиточек. Тогда вопрос о том, возможно ли бесконечное замощение, эквивалентен вопросу о том, возможна ли установка для машины Тьюринга, которая даст ей возможность не останавливаться. Дело в том, что, если машина Тьюринга универсальна (то есть ее можно запрограммировать для выполнения любых возможных вычислений), то проблема остановки для нее может быть неразрешимой, что означает, что проблема замощения также будет неразрешимой.

Конечно, это зависит от исходного набора форм. Вопрос заключается в том, насколько сложными должны быть формы, чтобы кодировать универсальные вычисления и приводить к нерешимой проблеме замощения. Соломон Голомб знал о литературе по этой теме, но не был особо заинтересован в ней.

Известно, что сложные и тщательно разработанные наборы полимино фактически поддерживают универсальные вычисления. Но что насчет простого набора? Действительно ли он достаточно простой для того, чтобы случайно наткнуться на него? Если посмотреть на все те системы, которые я изучал, то самый простой набор действительно оказывается простым. Однако найти его сложно.

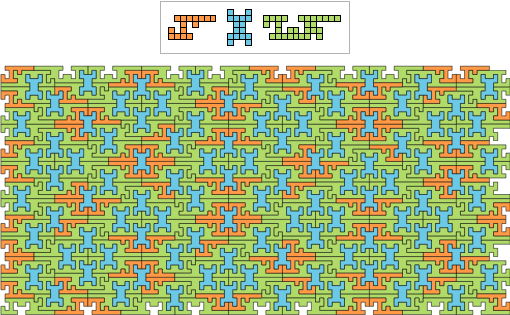
Значительно более простая задача заключается в нахождении полиомино, которые успешно заполняют плоскости, хотя и только непериодически. Роджер Пенроуз в 1994 году нашел подходящий пример. В моей книге Новый вид науки я привел немного более простой пример с 3 полиомино:

Остальная часть истории

Солу было чуть за тридцать, когда он достиг заметного успеха в области регистров сдвига и полиомино… Он был очень активным человеком. Он написал несколько сотен статей, часть из которых расширяла его более ранние работы, часть представляла собой ответы на вопросы, которые ему задавали, а некоторые были написаны, кажется, просто ради удовольствия — чтобы выяснить интересные вещи о числах, последовательностях, криптосистемах и т. д.

Регистры сдвига и полиомино — объемные темы (они даже выведены в отдельные категории в AMS классификации). В последние десятилетия они обе получили новый виток развития, когда на их основе стали проводить компьютерные эксперименты; Сол также принимал в них активное участие. Однако многие вопросы остаются без ответов. И если для регистров сдвига с линейной обратной связью можно найти большие матрицы Адамара, то даже сейчас о регистрах сдвига с нелинейной обратной связью мало что известно, не говоря уже обо всех непериодических и иных экзотических полиомино.

Сол всегда интересовался головоломками, — как математическими, так и со словами. Некоторое время он вел колонку головоломок для Los Angeles Times, и в течение 32 лет писал "гамбиты Голомба" в журнал для выпускников Джона Хопкинса. Он принимал участие в тестировании MegaIQ и выиграл поездку в Белый дом, когда он сам и его начальник вошли в пятерку лучших в стране.

Он вкладывал огромные усилия в свою работу в университете: не только обучал студентов и руководил аспирантами и восходил по административной лестнице (президент университетского совета, вице-проректор по исследованиям и др.), но и высказывал свое мнение об управлении университетом в целом (например, написал статью, озаглавленную «Консалтинг на факультете: убрать или оставить?»; Ответ: нет, это хорошо для университета!). В университете Южной Калифорнии он занимался хедхантингом, и за время своей работы там он помог университету подняться из неизвестности на вершину рейтинга образовательных программ.

А потом был консалтинг. Сол был дотошным и не раскрывал того, что делал для правительственных организаций. В конце 60-х гг., разочарованный тем, что все, кроме него занялись продажей игр на основе полиомино, Сол основал компанию, которую назвал Recreational Technology, Inc. Дела шли не слишком хорошо, однако Сол познакомился с Элвином Берлекэмпом — профессором из Беркли, который увлекался теориями кодирования и головоломками. Впоследствии они основали компанию Cyclotomics (в честь циклотомических многочленов вида xⁿ – 1), которая в итоге была продана компании Kodak за круглую сумму (Берлекэмп создал также алгоритмическую торговую систему, которую он затем продал Джиму Симонсу и которая стала отправной точкой для Renaissance Technologies — одного из крупнейших на сегодняшний день хедж-фондов).

Более 10000 патентов так или иначе связаны с работами Сола, а вот сам Сол получил только один патент на криптосистемы на основе квазигрупп — и я думаю, что он мало что сделал для коммерциализации своей работы.

На протяжении многих лет Сол работал с Технионом — израильским технологическим институтом. Он говорил о себе как о "нерелигиозном ортодоксальном еврее", но при этом иногда вел для новичков семинары по Книге Бытия, а также работал над расшифровкой частей свитков Мертвого моря (Кумранских рукописей).

Сол и его жена много путешествовали, однако «центром мира» для Сола определенно были его офис в Лос-Анджелесе в Университете Южной Калифорнии, и дом, в котором он и его жена жили в течение почти 60-ти лет. Он всегда был окружен друзьями и студентами. И у него была семья. Его дочь Астрид сыграла роль студентки в пьесе о Ричарде Фейнмане (она позировала ему), и в романе моего друга в качестве одного из персонажей. Беатрис посвятила свою карьеру применению математического уровня точности к различным видам медицинского показаний и диагностики (болезни, связанные с войной в Персидском заливе, эффекты статинов, приступы икоты и т. д.). Я даже внес свой небольшой вклад в жизнь Беатрис, познакомив ее с человеком, который стал затем ее мужем — с Терри Сейновски, одним из основателей современной вычислительной нейронауки.

Казалось, что Сол вовлечен во множество событий, даже если он не слишком распространялся о деталях. Время от времени мне хотелось поговорить с ним о науке и математике, но ему интереснее было рассказывать истории (часто очень увлекательные) как об отдельных личностях, так и об организациях ("Можете ли вы поверить, что [в 1985 году], после многолетнего отсутствия на конференциях, Клод Шеннон просто появился без предупреждения в баре на ежегодной конференции по теории информации?"; "вы знаете, сколько они должны были заплатить главе Калифорнийского технологического института, чтобы заставить его поехать в Саудовскую Аравию?», и т. д.).

Оглядываясь назад, я понимаю, что хотел бы заинтересовать Сола в решении некоторых математических вопросов, поднятых в моей работе. Думаю, что я так и не понял, до какой степени он любил решать проблемы, предложенные другими людьми. Несмотря на значительный вклад в развитие инфраструктуры вычислительного мира, сам Сол никогда всерьез не использовал компьютеры. Он очень гордился тем, что может с легкостью проводить вычисления в уме. До 70-ти лет он не пользовался электронной почтой и никогда не пользовался компьютером дома, хотя вот мобильный телефон у него был (обычной электронной почты от него почти не приходило. Я упомянул как-то, что около года назад я изучал историю Ады Лавлейс; он ответил: "История Ады Лавлейс как программиста Бэббиджа настолько широко распространена, что все, кажется, принимают ее как факт, однако я никогда не видел источников по этому вопросу.").

Дочери Сола несколько лет назад организовали вечеринку по поводу его 80-летия и создали такие интересные приглашения:



У Сола были определенные проблемы со здоровьем, хотя, казалось, это не очень отражается на его ритме жизни. Здоровье его жены ухудшалось, и в последние несколько недель довольно резко. В пятницу Сол, как обычно, пошел в свой кабинет, а в субботу ночью умер во сне. Его жена Бо пережила его всего на две недели и умерла всего за два дня до 60-й годовщины их свадьбы.

Хотя Сол и ушел, его работа живет в октиллионах бит в цифровом мире.

Прощай, Сол. И от всех нас — спасибо.