Урок №2. Создание треугольников
Основу кода и идеи я черпал отсюда:
1. Сатия Коматинени, Дэйв Маклин, Саид Хашими. Android 3 для профессионалов. Создание приложений для планшетных компьютеров и смартфонов.: Пер. с англ. – М.: ООО «И.Д.Вильямс». 2012 – 1024 с.
2. http://www.learnopengles.com/android-lesson-one-getting-started/
На первом уроке (можно посмотреть здесь https://habrahabr.ru/post/278895/ или здесь albatrossgames.blogspot.com/2016/03/opengl-es-2-android-1-opengl.html#more ) мы с вами научились заливать экран одним цветом с помощью OpenGL ES. Пришла пора рисовать треугольники, а точнее, с помощью треугольников мы нарисуем парусник, который будет циклично двигаться слева направо.

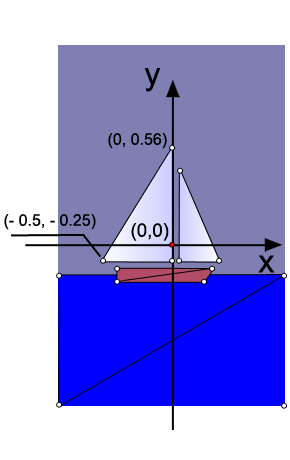
Почему треугольники? Дело в том, что в OpenGL есть только три графических примитива: точка, линия и треугольник. Корпус яхты (трапеция) и море (прямоугольник) нарисованы тоже с помощью треугольников. Как известно, точку в нашем пространстве определяют три координаты (x, y, z). Так как наш рисунок плоский, то у всех точек рисунка одна координата по оси 0z (она перпендикулярна плоскости экрана и идет на нас) будет равна нулю. Для примера я указал координаты по оси 0х и 0у двух крайних точек большого паруса (грота).
 " alt=«image2»/>
" alt=«image2»/>
В коде определение трех точек грота выглядит так:
Как вы видите, создается массив данных с плавающей запятой. Для каждой точки указывается её координата и цветовая гамма. Первая точка у нас белая, поэтому весовые коэффициенты у красного, зеленого и синего одинаковы и равны 1, а вот две остальные вершины я подсинил для красоты. Обход точек делается против часовой стрелки
Размерность координат в OpenGL условная и будет фактически определяться количеством пикселей экрана устройства по ширине и высоте.
Теперь нужно создать буфер, куда мы перекачаем данные о точках для OpenGL. Связано это с тем, что OpenGL написан на С-подобном языке. Поэтому мы переводим наши данные в другой вид, понятный для OpenGL, выделяя память.
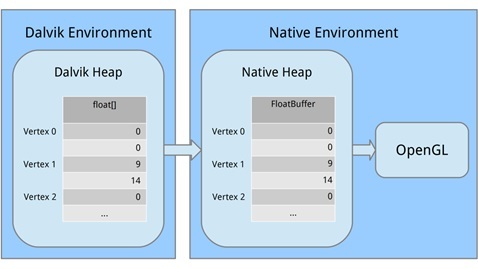
Давайте рассмотрим каждую часть. Во-первых, мы выделили блок машинной памяти, используя ByteBuffer.allocateDirect (); эта память не будет управляться Сборщиком мусора (что важно). Необходимо сказать методу, насколько большой блок памяти должен быть в байтах. Так как наши вершины хранятся в массиве в виде переменных float и занимают 4 байта на каждый float, мы передаем triangle1VerticesData.length * mBytesPerFloat. (Напомню, что private final int mBytesPerFloat = 4;)
Следующая строка говорит байтовому буферу, как он должен организовывать свои байты в машинном коде. Когда дело доходит до значений, которые охватывают несколько байтов, таких как 32-разрядные целые числа, байты можно записывать в разном порядке, например, от наиболее значимого значения до наименее значимого. Это похоже на написание большого числа либо слева направо или справа налево. Нам это всё равно, но важно то, что мы используем один и тот же порядок, что и система. Мы организуем это, вызывая order(ByteOrder.nativeOrder()). Наконец, лучше не иметь дело с отдельными байтами напрямую. Мы хотим работать с floats, поэтому вызываем FloatBuffer (), чтобы получить FloatBuffer, который содержит основные байты. Затем копируем, начиная с нулевой позиции, данные из памяти Dalvik в машинную память, вызывая mTriangle1Vertices.put(triangle1VerticesData).position(0);
Память будет освобождена, когда процесс прекращается, поэтому нам не нужно беспокоиться об этом.
Понимание матриц
Хороший урок для понимания матриц www.songho.ca/opengl/gl_transform.html
Чтобы понять матрицы, нужно для начала разобраться, как мы «видим» объект в OpenGL.
Представьте, что вы держите в руках фотоаппарат и хотите сфотографировать наш парусник.
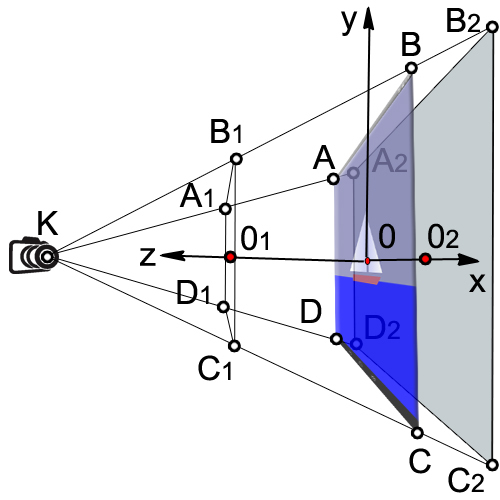
Пусть наша камера находится в т.К, эта точка называется точкой обзора. Если в коде мы не укажем точку обзора, камера будет по умолчанию в т.О с координатами (0,0,0).
Посмотрим, как задается положение камеры в коде:
В начале, мы установили цвет фона сине-серый, аналогично, как делали в первом занятии.
Потом разместили камеру, фактически указали координаты т.К. Как вы видите, камера у нас сдвинута по оси 0z на 1,5 единицы (расстояние ОК).
В следующих строчках кода мы устанавливаем максимальную дальность, на которую видит камера, это координата т. 02.
Таким образом, высота нашей пирамиды К02 = 10.
Следующие строчки кода определяют, как ориентирована камера или положение up vector. Из-за неудачных переводов, в разных статьях допущены неточности в этом вопросе. В нашем коде сейчас
Это значит, что камера размещена обычно, так, если бы вы положили её на горизонтальный стол и смотрит на парусник в т.0.

Теперь представьте, что из камеры выходят три вектора, как из т.О. Поставив весовой коэффициент final float upY = 1.0f, мы говорим OpenGL, что вверх будет направлена ось 0У и видим картинку, как в начале статьи.
Но стоит нам поставить вот такие коэффициенты
мы увидим на эмуляторе следующее. Наш парусник будет карабкаться по наклонной вверх.
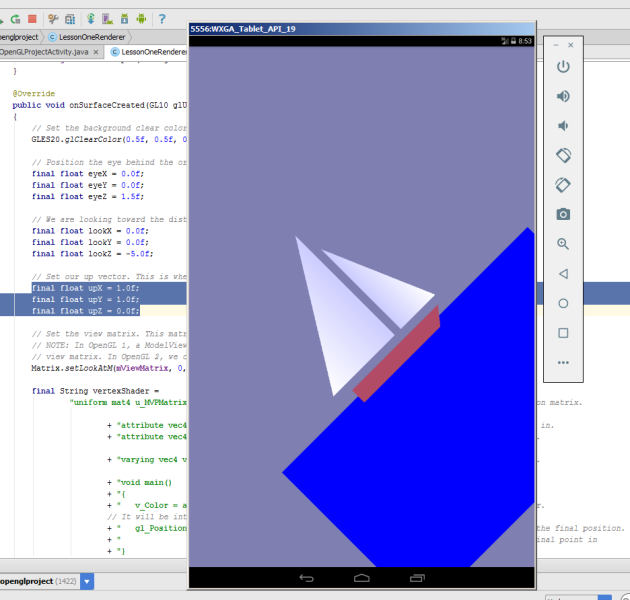
Камера повернулась на 45 градусов против часовой стрелки, если смотреть на ось 0z. Понятно, что если сделать такую комбинацию
вверх будет смотреть ось 0х камеры и кораблик будет плыть вертикально вверх.
Все наши данные мы передаем методу setLookAtM.
Matrix.setLookAtM(mViewMatrix, 0, eyeX, eyeY, eyeZ, lookX, lookY, lookZ, upX, upY, upZ);
Видимый объем камеры
Рассмотрим следующий кусок кода.
Метод onSurfaceChanged позволяет отработать изменение ориентации самого устройства.
Повернем на эмуляторе наш гаджет и видим такую картину

Не очень красиво, но в принципе то, что мы нарисовали.
Следующая строчка кода устанавливает размер экрана. Сначала устанавливаем координаты нижней точки левого угла экрана (0,0), а потом ширину и высоту экрана.
GLES20.glViewport(0, 0, width, height);
Давайте еще раз рассмотрим наш рисунок:

Объем, который видит наша камера, заключен в объеме усеченной пирамиды (A1,B1,C1,D1, A2,B2,C2,D2).
Сначала мы находим отношение ширины к высоте устройства (ratio).
final float ratio = (float) width / height;
Потом задаем координату по 0х левой и правой стороны видимого параллелепипеда (A1,B1,C1,D1).
final float left = -ratio;
final float right = ratio;
Задаем координату по 0у нижней и верхней стороны параллелепипеда (A1,B1,C1,D1).
final float bottom = -1.0f;
final float top = 1.0f;
Расстояние от камеры до передней стороны (КО1)
final float near = 1.0f;
Расстояние от камеры до задней стороны (КО2)
final float far = 10.0f;
Применяем матричное преобразование
Matrix.frustumM(mProjectionMatrix, 0, left, right, bottom, top, near, far);
Есть несколько различных видов матриц, которые мы используем:
1. Матрица модели. Эта матрица используется для размещения модели где-то в «мире». Например, если у вас есть модель автомобиля, и вы захотите расположить её на расстоянии 1000 м на восток, вы будете использовать матрицу модели.
2. Матрица вида. Эта матрица представляет собой камеру. Если мы хотим, посмотреть на нашу машину, которая находится в 1000 м на восток, мы должны передвинуть себя на 1000 м на восток. Или можно остаться неподвижными, а весь остальной мир передвинуть на 1000 м на запад. Чтобы сделать это, мы будем использовать матрицу вида.
3. Матрица проекции. Так как наши экраны являются плоскими, то нам нужно сделать окончательное преобразование в «проект» нашего вида на экране и получить 3D-перспективу. Для этого используют матрицу проекции.
Определение вершинных и фрагментных шейдеров
Даже самые простые рисунки в OpenGL ES 2.0 требуют создания программных сегментов, которые называются шейдерами. Шейдеры формируют ядро OpenGL ES 2.0. Вершины обрабатываются вершинными шейдерами и имеют дело только с точками вершин. Пространства между вершинами обрабатывают с помощью фрагментных шейдеров, они имею дело с каждым пикселем на экране.
Для написания шейдеров используют язык программирования OpenGL Shading Language (GLSL).
Каждый шейдер в основном состоит из ввода, вывода и программы. Сначала мы определяем форму, которая представляет собой комбинированную матрицу, содержащую все наши преобразования. Она постоянна для всех вершин и используется для проецирования их на экран. Затем мы определяем два атрибута для позиции и цвета. Эти атрибуты будут прочитаны из буфера, которое мы определили ранее, они задают положение и цвет каждой вершины. Затем мы определим варьирование (изменение цвета), который интерполирует значения для всего треугольника и передаст его во фрагментный шейдер. Когда дело доходит до фрагментного шейдера, то он будет содержать интерполированное значение для каждого пикселя.
Скажем, мы определили треугольник, у которого вершины будут красная, зеленая и синяя, а его размер будет занимать 10 пикселей на экране. При выполнении фрагментного шейдера, он будет содержать различный изменяющийся цвет для каждого пикселя. В какой-то точке, что изменение будет красным, но на полпути между красным и синим, это может быть пурпурный цвет.
Рассмотрим наш вершинный шейдер
Через униформы (uniform) в шейдеры передаются внешние данные, которые могут быть использованы для расчетов. Униформы могут быть использованы только для чтения. Униформы могут быть переданы как в вершинный, так и в фрагментный шейдеры. В нашем случае униформа одна — это матрица модели-вида-проекции u_MVPMatrix и передается она в вершинный шейдер. Ключевое слово mat4 означает, что это матрица размером 4х4 состоящая из чисел с плавающей точкой. Униформы никак не связаны с конкретной вершиной и являются глобальными константами. Для названия униформ обычно используют префикс u_.
Атрибуты (attribute) — это свойство вершины. У вершины могут быть различные атрибуты. Например, координаты положения в пространстве, координаты вектора нормали, цвет. Кроме того, вы можете передавать в вершинный шейдер какие-либо свои атрибуты. Важно понять, что атрибут-это свойство вершины и поэтому он должен быть задан для каждой вершины. Атрибуты передаются только в вершинный шейдер. Атрибуты доступны вершинному шейдеру только для чтения. Нельзя определять атрибуты во фрагментном шейдере. В дальнейшем для удобства будем обозначать атрибуты с префиксом a_.
Определим в вершинном шейдере три атрибута:
attribute vec4 a_Position;
Переменная a_Position – атрибут вершины, который имеет дело с положением вершины (координатами), это четырехкомпанентный вектор (vec4).
Атрибут цвета вершины
attribute vec4 a_Color;
Атрибут интерполяции цвета
varying vec4 v_Color;
Рассмотрим код функции main подробнее:
v_Color = a_Color;
Передаем информацию о цвете вершин во фрагментный шейдер.
gl_Position = u_MVPMatrix * a_Position;
Трансформируем положение вершин с помощью матрицы и записываем в новую переменную gl_Position.
Системная переменная gl_Position — это четырех-компонентный вектор, определяющий координаты вершины, спроецированные на плоскость экрана. Переменная gl_Position обязательно должна быть определена в вершинном шейдере, иначе на экране мы ничего не увидим.
Приступим к рассмотрению фрагментного шейдера.
Точность по умолчанию устанавливаем среднюю, так как она не нужна нам высокой в случае фрагментного шейдера. В вершинном шейдере точность по умолчанию высокая.
precision mediump float;
Конечная цель фрагментного шейдера — это получение цвета пикселя. Рассчитанный цвет пикселя должен быть обязательно записан в системную переменную gl_FragColor. В нашем простейшем примере мы не вычисляем цвет пикселя во фрагментном шейдере, а просто присваиваем значение цвета v_color, полученного путем интерполяции из цветов вершин:
gl_FragColor = v_color;
Загрузка шейдеров в OpenGL
Связывание вершинного и фрагментного шейдеров вместе в программе
Перед тем как использовать наши вершинный и фрагментный шейдеры, нам нужно связать их вместе в программе. Это то, что соединяет выход вершинного шейдера со входом фрагментного шейдера. Это также то, что позволяет нам передать входные данные из нашей программы и использовать шейдеры, чтобы рисовать наши фигуры.
Мы создаем новый программный объект, и если это удалось, мы затем присоединяем наши шейдеры. Мы хотим передать данные о положении и цвете, как атрибуты, так что нам нужно, чтобы связать эти атрибуты. Затем свяжем шейдеры вместе.
После того как мы успешно связали нашу программу, мы закончим с парой больших задач, теперь мы реально можем использовать её. Первая задача заключается в получении ссылок, поэтому мы можем передавать данные в программу. Тогда мы говорим OpenGL использовать эту программу, когда происходит рисование. Так как мы используем только одну программу в этом уроке, мы можем поставить это в onSurfaceCreated () вместо onDrawFrame ().
Установка перспективной проекции
Наш метод onSurfaceChanged () вызывается по крайней мере один раз, а также всякий раз, когда наша поверхность изменяется. Так как нам надо сбрасывать нашу матрицу проекции всякий раз, когда на экране проецирование изменилась, то onSurfaceChanged () является идеальным местом, чтобы сделать это.
Вывод объектов на экран
Вывод производим в методе onDrawFrame(GL10 glUnused)
Чтобы треугольники двигались по оси 0х, применяем матрицу перемещения и задаем увеличение смещения по х на 0,001 за каждое обновление поверхности. Как только х достигает 1 или правого края экрана, обнуляем его.
Matrix.translateM(mModelMatrix, 0, x + 0.3f, 0.0f, 0.0f);
drawTriangle(mTriangle2Vertices);
if(x<=1){x = (float) (x + 0.001);}
else {x=0;}
Думаю для второго урока более чем достаточно. Многие вопросы упущены, и понимание их придет позже.
Запуск урока на Андроид Студио.
Я рекомендую использовать проект предыдущего урока и просто скопировать в него данный код.
Если у вас его нет, то создайте проект First Open GL Project
AndroidManifest.xml
FirstOpenGLProjectActivity.java
LessonOneRenderer.java
1. Сатия Коматинени, Дэйв Маклин, Саид Хашими. Android 3 для профессионалов. Создание приложений для планшетных компьютеров и смартфонов.: Пер. с англ. – М.: ООО «И.Д.Вильямс». 2012 – 1024 с.
2. http://www.learnopengles.com/android-lesson-one-getting-started/
3. http://andmonahov.blogspot.com/2012/10/opengl-es-20-1.html
4. https://www.opengl.org/sdk/docs/tutorials/ClockworkCoders/attributes.php
5. https://www.khronos.org/opengles/sdk/docs/reference_cards/OpenGL-ES-2_0-Reference-card.pdf
Основу кода и идеи я черпал отсюда:
1. Сатия Коматинени, Дэйв Маклин, Саид Хашими. Android 3 для профессионалов. Создание приложений для планшетных компьютеров и смартфонов.: Пер. с англ. – М.: ООО «И.Д.Вильямс». 2012 – 1024 с.
2. http://www.learnopengles.com/android-lesson-one-getting-started/
На первом уроке (можно посмотреть здесь https://habrahabr.ru/post/278895/ или здесь albatrossgames.blogspot.com/2016/03/opengl-es-2-android-1-opengl.html#more ) мы с вами научились заливать экран одним цветом с помощью OpenGL ES. Пришла пора рисовать треугольники, а точнее, с помощью треугольников мы нарисуем парусник, который будет циклично двигаться слева направо.

Почему треугольники? Дело в том, что в OpenGL есть только три графических примитива: точка, линия и треугольник. Корпус яхты (трапеция) и море (прямоугольник) нарисованы тоже с помощью треугольников. Как известно, точку в нашем пространстве определяют три координаты (x, y, z). Так как наш рисунок плоский, то у всех точек рисунка одна координата по оси 0z (она перпендикулярна плоскости экрана и идет на нас) будет равна нулю. Для примера я указал координаты по оси 0х и 0у двух крайних точек большого паруса (грота).
 " alt=«image2»/>
" alt=«image2»/>В коде определение трех точек грота выглядит так:
// this triangle is white-blue. First sail is mainsail
final float[] triangle1VerticesData = {
// X, Y, Z,
// R, G, B, A
-0.5f, -0.25f, 0.0f,
1.0f, 1.0f, 1.0f, 1.0f,
0.0f, -0.25f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f,
0.0f, 0.56f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f};
Как вы видите, создается массив данных с плавающей запятой. Для каждой точки указывается её координата и цветовая гамма. Первая точка у нас белая, поэтому весовые коэффициенты у красного, зеленого и синего одинаковы и равны 1, а вот две остальные вершины я подсинил для красоты. Обход точек делается против часовой стрелки
Размерность координат в OpenGL условная и будет фактически определяться количеством пикселей экрана устройства по ширине и высоте.
Теперь нужно создать буфер, куда мы перекачаем данные о точках для OpenGL. Связано это с тем, что OpenGL написан на С-подобном языке. Поэтому мы переводим наши данные в другой вид, понятный для OpenGL, выделяя память.
/** How many bytes per float. */
private final int mBytesPerFloat = 4;
// Initialize the buffers.
mTriangle1Vertices = ByteBuffer.allocateDirect(triangle1VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle1Vertices.put(triangle1VerticesData).position(0);

Давайте рассмотрим каждую часть. Во-первых, мы выделили блок машинной памяти, используя ByteBuffer.allocateDirect (); эта память не будет управляться Сборщиком мусора (что важно). Необходимо сказать методу, насколько большой блок памяти должен быть в байтах. Так как наши вершины хранятся в массиве в виде переменных float и занимают 4 байта на каждый float, мы передаем triangle1VerticesData.length * mBytesPerFloat. (Напомню, что private final int mBytesPerFloat = 4;)
Следующая строка говорит байтовому буферу, как он должен организовывать свои байты в машинном коде. Когда дело доходит до значений, которые охватывают несколько байтов, таких как 32-разрядные целые числа, байты можно записывать в разном порядке, например, от наиболее значимого значения до наименее значимого. Это похоже на написание большого числа либо слева направо или справа налево. Нам это всё равно, но важно то, что мы используем один и тот же порядок, что и система. Мы организуем это, вызывая order(ByteOrder.nativeOrder()). Наконец, лучше не иметь дело с отдельными байтами напрямую. Мы хотим работать с floats, поэтому вызываем FloatBuffer (), чтобы получить FloatBuffer, который содержит основные байты. Затем копируем, начиная с нулевой позиции, данные из памяти Dalvik в машинную память, вызывая mTriangle1Vertices.put(triangle1VerticesData).position(0);
Память будет освобождена, когда процесс прекращается, поэтому нам не нужно беспокоиться об этом.
Понимание матриц
Хороший урок для понимания матриц www.songho.ca/opengl/gl_transform.html
Чтобы понять матрицы, нужно для начала разобраться, как мы «видим» объект в OpenGL.
Представьте, что вы держите в руках фотоаппарат и хотите сфотографировать наш парусник.

Пусть наша камера находится в т.К, эта точка называется точкой обзора. Если в коде мы не укажем точку обзора, камера будет по умолчанию в т.О с координатами (0,0,0).
Посмотрим, как задается положение камеры в коде:
@Override
public void onSurfaceCreated(GL10 glUnused, EGLConfig config)
{
// Set the background clear color to gray.
GLES20.glClearColor(0.5f, 0.5f, 0.7f, 1.0f);
// Position the eye behind the origin.
final float eyeX = 0.0f;
final float eyeY = 0.0f;
final float eyeZ = 1.5f;
// We are looking toward the distance
final float lookX = 0.0f;
final float lookY = 0.0f;
final float lookZ = -5.0f;
// Set our up vector. This is where our head would be pointing were we holding the camera.
final float upX = 0.0f;
final float upY = 1.0f;
final float upZ = 0.0f;
// Set the view matrix. This matrix can be said to represent the camera position.
// NOTE: In OpenGL 1, a ModelView matrix is used, which is a combination of a model and
// view matrix. In OpenGL 2, we can keep track of these matrices separately if we choose.
Matrix.setLookAtM(mViewMatrix, 0, eyeX, eyeY, eyeZ, lookX, lookY, lookZ, upX, upY, upZ);
В начале, мы установили цвет фона сине-серый, аналогично, как делали в первом занятии.
GLES20.glClearColor(0.5f, 0.5f, 0.7f, 1.0f);
Потом разместили камеру, фактически указали координаты т.К. Как вы видите, камера у нас сдвинута по оси 0z на 1,5 единицы (расстояние ОК).
final float eyeX = 0.0f;
final float eyeY = 0.0f;
final float eyeZ = 1.5f;
В следующих строчках кода мы устанавливаем максимальную дальность, на которую видит камера, это координата т. 02.
final float lookX = 0.0f;
final float lookY = 0.0f;
final float lookZ = -5.0f;
Таким образом, высота нашей пирамиды К02 = 10.
Следующие строчки кода определяют, как ориентирована камера или положение up vector. Из-за неудачных переводов, в разных статьях допущены неточности в этом вопросе. В нашем коде сейчас
final float upX = 0.0f;
final float upY = 1.0f;
final float upZ = 0.0f;
Это значит, что камера размещена обычно, так, если бы вы положили её на горизонтальный стол и смотрит на парусник в т.0.

Теперь представьте, что из камеры выходят три вектора, как из т.О. Поставив весовой коэффициент final float upY = 1.0f, мы говорим OpenGL, что вверх будет направлена ось 0У и видим картинку, как в начале статьи.
Но стоит нам поставить вот такие коэффициенты
final float upX = 1.0f;
final float upY = 1.0f;
final float upZ = 0.0f;
мы увидим на эмуляторе следующее. Наш парусник будет карабкаться по наклонной вверх.

Камера повернулась на 45 градусов против часовой стрелки, если смотреть на ось 0z. Понятно, что если сделать такую комбинацию
final float upX = 1.0f;
final float upY = 0.0f;
final float upZ = 0.0f;
вверх будет смотреть ось 0х камеры и кораблик будет плыть вертикально вверх.
Все наши данные мы передаем методу setLookAtM.
Matrix.setLookAtM(mViewMatrix, 0, eyeX, eyeY, eyeZ, lookX, lookY, lookZ, upX, upY, upZ);
Видимый объем камеры
Рассмотрим следующий кусок кода.
@Override
public void onSurfaceChanged(GL10 glUnused, int width, int height)
{
// Set the OpenGL viewport to the same size as the surface.
GLES20.glViewport(0, 0, width, height);
// Create a new perspective projection matrix. The height will stay the same
// while the width will vary as per aspect ratio.
final float ratio = (float) width / height;
final float left = -ratio;
final float right = ratio;
final float bottom = -1.0f;
final float top = 1.0f;
final float near = 1.0f;
final float far = 10.0f;
Matrix.frustumM(mProjectionMatrix, 0, left, right, bottom, top, near, far);
}
Метод onSurfaceChanged позволяет отработать изменение ориентации самого устройства.
Повернем на эмуляторе наш гаджет и видим такую картину

Не очень красиво, но в принципе то, что мы нарисовали.
Следующая строчка кода устанавливает размер экрана. Сначала устанавливаем координаты нижней точки левого угла экрана (0,0), а потом ширину и высоту экрана.
GLES20.glViewport(0, 0, width, height);
Давайте еще раз рассмотрим наш рисунок:

Объем, который видит наша камера, заключен в объеме усеченной пирамиды (A1,B1,C1,D1, A2,B2,C2,D2).
Сначала мы находим отношение ширины к высоте устройства (ratio).
final float ratio = (float) width / height;
Потом задаем координату по 0х левой и правой стороны видимого параллелепипеда (A1,B1,C1,D1).
final float left = -ratio;
final float right = ratio;
Задаем координату по 0у нижней и верхней стороны параллелепипеда (A1,B1,C1,D1).
final float bottom = -1.0f;
final float top = 1.0f;
Расстояние от камеры до передней стороны (КО1)
final float near = 1.0f;
Расстояние от камеры до задней стороны (КО2)
final float far = 10.0f;
Применяем матричное преобразование
Matrix.frustumM(mProjectionMatrix, 0, left, right, bottom, top, near, far);
Есть несколько различных видов матриц, которые мы используем:
1. Матрица модели. Эта матрица используется для размещения модели где-то в «мире». Например, если у вас есть модель автомобиля, и вы захотите расположить её на расстоянии 1000 м на восток, вы будете использовать матрицу модели.
2. Матрица вида. Эта матрица представляет собой камеру. Если мы хотим, посмотреть на нашу машину, которая находится в 1000 м на восток, мы должны передвинуть себя на 1000 м на восток. Или можно остаться неподвижными, а весь остальной мир передвинуть на 1000 м на запад. Чтобы сделать это, мы будем использовать матрицу вида.
3. Матрица проекции. Так как наши экраны являются плоскими, то нам нужно сделать окончательное преобразование в «проект» нашего вида на экране и получить 3D-перспективу. Для этого используют матрицу проекции.
Определение вершинных и фрагментных шейдеров
Даже самые простые рисунки в OpenGL ES 2.0 требуют создания программных сегментов, которые называются шейдерами. Шейдеры формируют ядро OpenGL ES 2.0. Вершины обрабатываются вершинными шейдерами и имеют дело только с точками вершин. Пространства между вершинами обрабатывают с помощью фрагментных шейдеров, они имею дело с каждым пикселем на экране.
Для написания шейдеров используют язык программирования OpenGL Shading Language (GLSL).
Каждый шейдер в основном состоит из ввода, вывода и программы. Сначала мы определяем форму, которая представляет собой комбинированную матрицу, содержащую все наши преобразования. Она постоянна для всех вершин и используется для проецирования их на экран. Затем мы определяем два атрибута для позиции и цвета. Эти атрибуты будут прочитаны из буфера, которое мы определили ранее, они задают положение и цвет каждой вершины. Затем мы определим варьирование (изменение цвета), который интерполирует значения для всего треугольника и передаст его во фрагментный шейдер. Когда дело доходит до фрагментного шейдера, то он будет содержать интерполированное значение для каждого пикселя.
Скажем, мы определили треугольник, у которого вершины будут красная, зеленая и синяя, а его размер будет занимать 10 пикселей на экране. При выполнении фрагментного шейдера, он будет содержать различный изменяющийся цвет для каждого пикселя. В какой-то точке, что изменение будет красным, но на полпути между красным и синим, это может быть пурпурный цвет.
Рассмотрим наш вершинный шейдер
final String vertexShader =
"uniform mat4 u_MVPMatrix; \n" // A constant representing the combined model/view/projection matrix.
+ "attribute vec4 a_Position; \n" // Per-vertex position information we will pass in.
+ "attribute vec4 a_Color; \n" // Per-vertex color information we will pass in.
+ "varying vec4 v_Color; \n" // This will be passed into the fragment shader.
+ "void main() \n" // The entry point for our vertex shader.
+ "{ \n"
+ " v_Color = a_Color; \n" // Pass the color through to the fragment shader.
// It will be interpolated across the triangle.
+ " gl_Position = u_MVPMatrix \n" // gl_Position is a special variable used to store the final position.
+ " * a_Position; \n" // Multiply the vertex by the matrix to get the final point in
+ "} \n"; // normalized screen coordinates.
Через униформы (uniform) в шейдеры передаются внешние данные, которые могут быть использованы для расчетов. Униформы могут быть использованы только для чтения. Униформы могут быть переданы как в вершинный, так и в фрагментный шейдеры. В нашем случае униформа одна — это матрица модели-вида-проекции u_MVPMatrix и передается она в вершинный шейдер. Ключевое слово mat4 означает, что это матрица размером 4х4 состоящая из чисел с плавающей точкой. Униформы никак не связаны с конкретной вершиной и являются глобальными константами. Для названия униформ обычно используют префикс u_.
Атрибуты (attribute) — это свойство вершины. У вершины могут быть различные атрибуты. Например, координаты положения в пространстве, координаты вектора нормали, цвет. Кроме того, вы можете передавать в вершинный шейдер какие-либо свои атрибуты. Важно понять, что атрибут-это свойство вершины и поэтому он должен быть задан для каждой вершины. Атрибуты передаются только в вершинный шейдер. Атрибуты доступны вершинному шейдеру только для чтения. Нельзя определять атрибуты во фрагментном шейдере. В дальнейшем для удобства будем обозначать атрибуты с префиксом a_.
Определим в вершинном шейдере три атрибута:
attribute vec4 a_Position;
Переменная a_Position – атрибут вершины, который имеет дело с положением вершины (координатами), это четырехкомпанентный вектор (vec4).
Атрибут цвета вершины
attribute vec4 a_Color;
Атрибут интерполяции цвета
varying vec4 v_Color;
Рассмотрим код функции main подробнее:
v_Color = a_Color;
Передаем информацию о цвете вершин во фрагментный шейдер.
gl_Position = u_MVPMatrix * a_Position;
Трансформируем положение вершин с помощью матрицы и записываем в новую переменную gl_Position.
Системная переменная gl_Position — это четырех-компонентный вектор, определяющий координаты вершины, спроецированные на плоскость экрана. Переменная gl_Position обязательно должна быть определена в вершинном шейдере, иначе на экране мы ничего не увидим.
Приступим к рассмотрению фрагментного шейдера.
final String fragmentShader =
"precision mediump float; \n" // Set the default precision to medium. We don't need as high of a
// precision in the fragment shader.
+ "varying vec4 v_Color; \n" // This is the color from the vertex shader interpolated across the
// triangle per fragment.
+ "void main() \n" // The entry point for our fragment shader.
+ "{ \n"
+ " gl_FragColor = v_Color; \n" // Pass the color directly through the pipeline.
+ "} \n";
Точность по умолчанию устанавливаем среднюю, так как она не нужна нам высокой в случае фрагментного шейдера. В вершинном шейдере точность по умолчанию высокая.
precision mediump float;
Конечная цель фрагментного шейдера — это получение цвета пикселя. Рассчитанный цвет пикселя должен быть обязательно записан в системную переменную gl_FragColor. В нашем простейшем примере мы не вычисляем цвет пикселя во фрагментном шейдере, а просто присваиваем значение цвета v_color, полученного путем интерполяции из цветов вершин:
gl_FragColor = v_color;
Загрузка шейдеров в OpenGL
// Load in the vertex shader.
int vertexShaderHandle = GLES20.glCreateShader(GLES20.GL_VERTEX_SHADER);
if (vertexShaderHandle != 0)
{
// Pass in the shader source.
GLES20.glShaderSource(vertexShaderHandle, vertexShader);
// Compile the shader.
GLES20.glCompileShader(vertexShaderHandle);
// Get the compilation status.
final int[] compileStatus = new int[1];
GLES20.glGetShaderiv(vertexShaderHandle, GLES20.GL_COMPILE_STATUS, compileStatus, 0);
// If the compilation failed, delete the shader.
if (compileStatus[0] == 0)
{
GLES20.glDeleteShader(vertexShaderHandle);
vertexShaderHandle = 0;
}
}
if (vertexShaderHandle == 0)
{
throw new RuntimeException("Error creating vertex shader.");
}
Связывание вершинного и фрагментного шейдеров вместе в программе
// Create a program object and store the handle to it.
int programHandle = GLES20.glCreateProgram();
if (programHandle != 0)
{
// Bind the vertex shader to the program.
GLES20.glAttachShader(programHandle, vertexShaderHandle);
// Bind the fragment shader to the program.
GLES20.glAttachShader(programHandle, fragmentShaderHandle);
// Bind attributes
GLES20.glBindAttribLocation(programHandle, 0, "a_Position");
GLES20.glBindAttribLocation(programHandle, 1, "a_Color");
// Link the two shaders together into a program.
GLES20.glLinkProgram(programHandle);
// Get the link status.
final int[] linkStatus = new int[1];
GLES20.glGetProgramiv(programHandle, GLES20.GL_LINK_STATUS, linkStatus, 0);
// If the link failed, delete the program.
if (linkStatus[0] == 0)
{
GLES20.glDeleteProgram(programHandle);
programHandle = 0;
}
}
if (programHandle == 0)
{
throw new RuntimeException("Error creating program.");
}
Перед тем как использовать наши вершинный и фрагментный шейдеры, нам нужно связать их вместе в программе. Это то, что соединяет выход вершинного шейдера со входом фрагментного шейдера. Это также то, что позволяет нам передать входные данные из нашей программы и использовать шейдеры, чтобы рисовать наши фигуры.
Мы создаем новый программный объект, и если это удалось, мы затем присоединяем наши шейдеры. Мы хотим передать данные о положении и цвете, как атрибуты, так что нам нужно, чтобы связать эти атрибуты. Затем свяжем шейдеры вместе.
//New class members
/** This will be used to pass in the transformation matrix. */
private int mMVPMatrixHandle;
/** This will be used to pass in model position information. */
private int mPositionHandle;
/** This will be used to pass in model color information. */
private int mColorHandle;
@Override
public void onSurfaceCreated(GL10 glUnused, EGLConfig config)
{
...
// Set program handles. These will later be used to pass in values to the program.
mMVPMatrixHandle = GLES20.glGetUniformLocation(programHandle, "u_MVPMatrix");
mPositionHandle = GLES20.glGetAttribLocation(programHandle, "a_Position");
mColorHandle = GLES20.glGetAttribLocation(programHandle, "a_Color");
// Tell OpenGL to use this program when rendering.
GLES20.glUseProgram(programHandle);
}
После того как мы успешно связали нашу программу, мы закончим с парой больших задач, теперь мы реально можем использовать её. Первая задача заключается в получении ссылок, поэтому мы можем передавать данные в программу. Тогда мы говорим OpenGL использовать эту программу, когда происходит рисование. Так как мы используем только одну программу в этом уроке, мы можем поставить это в onSurfaceCreated () вместо onDrawFrame ().
Установка перспективной проекции
// New class members
/** Store the projection matrix. This is used to project the scene onto a 2D viewport. */
private float[] mProjectionMatrix = new float[16];
@Override
public void onSurfaceChanged(GL10 glUnused, int width, int height)
{
// Set the OpenGL viewport to the same size as the surface.
GLES20.glViewport(0, 0, width, height);
// Create a new perspective projection matrix. The height will stay the same
// while the width will vary as per aspect ratio.
final float ratio = (float) width / height;
final float left = -ratio;
final float right = ratio;
final float bottom = -1.0f;
final float top = 1.0f;
final float near = 1.0f;
final float far = 10.0f;
Matrix.frustumM(mProjectionMatrix, 0, left, right, bottom, top, near, far);
}
Наш метод onSurfaceChanged () вызывается по крайней мере один раз, а также всякий раз, когда наша поверхность изменяется. Так как нам надо сбрасывать нашу матрицу проекции всякий раз, когда на экране проецирование изменилась, то onSurfaceChanged () является идеальным местом, чтобы сделать это.
Вывод объектов на экран
Вывод производим в методе onDrawFrame(GL10 glUnused)
Чтобы треугольники двигались по оси 0х, применяем матрицу перемещения и задаем увеличение смещения по х на 0,001 за каждое обновление поверхности. Как только х достигает 1 или правого края экрана, обнуляем его.
Matrix.translateM(mModelMatrix, 0, x + 0.3f, 0.0f, 0.0f);
drawTriangle(mTriangle2Vertices);
if(x<=1){x = (float) (x + 0.001);}
else {x=0;}
Думаю для второго урока более чем достаточно. Многие вопросы упущены, и понимание их придет позже.
Запуск урока на Андроид Студио.
Я рекомендую использовать проект предыдущего урока и просто скопировать в него данный код.
Если у вас его нет, то создайте проект First Open GL Project
AndroidManifest.xml
<?xml version="1.0" encoding="utf-8"?>
<manifest xmlns:android="http://schemas.android.com/apk/res/android"
package="com.adc2017gmail.firstopenglproject">
<application
android:allowBackup="true"
android:icon="@mipmap/ic_launcher"
android:label="@string/app_name"
android:supportsRtl="true"
android:theme="@style/AppTheme">
<uses-feature
android:glEsVersion="0x00020000"
android:required="true" />
<activity android:name=".FirstOpenGLProjectActivity">
<intent-filter>
<action android:name="android.intent.action.MAIN" />
<category android:name="android.intent.category.LAUNCHER" />
</intent-filter>
</activity>
</application>
</manifest>
FirstOpenGLProjectActivity.java
package com.adc2017gmail.firstopenglproject;
import android.app.Activity;
import android.app.ActivityManager;
import android.content.Context;
import android.content.pm.ConfigurationInfo;
import android.opengl.GLSurfaceView;
import android.os.Bundle;
public class FirstOpenGLProjectActivity extends Activity
{
/** Hold a reference to our GLSurfaceView */
private GLSurfaceView mGLSurfaceView;
@Override
public void onCreate(Bundle savedInstanceState)
{
super.onCreate(savedInstanceState);
mGLSurfaceView = new GLSurfaceView(this);
// Check if the system supports OpenGL ES 2.0.
final ActivityManager activityManager = (ActivityManager) getSystemService(Context.ACTIVITY_SERVICE);
final ConfigurationInfo configurationInfo = activityManager.getDeviceConfigurationInfo();
final boolean supportsEs2 = configurationInfo.reqGlEsVersion >= 0x20000;
if (supportsEs2)
{
// Request an OpenGL ES 2.0 compatible context.
mGLSurfaceView.setEGLContextClientVersion(2);
// Set the renderer to our demo renderer, defined below.
mGLSurfaceView.setRenderer(new LessonOneRenderer());
}
else
{
// This is where you could create an OpenGL ES 1.x compatible
// renderer if you wanted to support both ES 1 and ES 2.
return;
}
setContentView(mGLSurfaceView);
}
@Override
protected void onResume()
{
// The activity must call the GL surface view's onResume() on activity onResume().
super.onResume();
mGLSurfaceView.onResume();
}
@Override
protected void onPause()
{
// The activity must call the GL surface view's onPause() on activity onPause().
super.onPause();
mGLSurfaceView.onPause();
}
}
LessonOneRenderer.java
package com.adc2017gmail.firstopenglproject;
import android.opengl.GLES20;
import android.opengl.GLSurfaceView;
import android.opengl.Matrix;
import java.nio.ByteBuffer;
import java.nio.ByteOrder;
import java.nio.FloatBuffer;
import javax.microedition.khronos.egl.EGLConfig;
import javax.microedition.khronos.opengles.GL10;
/**
* This class implements our custom renderer. Note that the GL10 parameter passed in is unused for OpenGL ES 2.0
* renderers -- the static class GLES20 is used instead.
*/
public class LessonOneRenderer implements GLSurfaceView.Renderer
{
/**
* Store the model matrix. This matrix is used to move models from object space (where each model can be thought
* of being located at the center of the universe) to world space.
*/
private float[] mModelMatrix = new float[16];
/**
* Store the view matrix. This can be thought of as our camera. This matrix transforms world space to eye space;
* it positions things relative to our eye.
*/
private float[] mViewMatrix = new float[16];
/** Store the projection matrix. This is used to project the scene onto a 2D viewport. */
private float[] mProjectionMatrix = new float[16];
/** Allocate storage for the final combined matrix. This will be passed into the shader program. */
private float[] mMVPMatrix = new float[16];
/** Store our model data in a float buffer. */
private final FloatBuffer mTriangle1Vertices;
private final FloatBuffer mTriangle2Vertices;
private final FloatBuffer mTriangle3Vertices;
private final FloatBuffer mTriangle4Vertices;
private final FloatBuffer mTriangle5Vertices;
private final FloatBuffer mTriangle6Vertices;
/** This will be used to pass in the transformation matrix. */
private int mMVPMatrixHandle;
/** This will be used to pass in model position information. */
private int mPositionHandle;
/** This will be used to pass in model color information. */
private int mColorHandle;
/** How many bytes per float. */
private final int mBytesPerFloat = 4;
/** How many elements per vertex. */
private final int mStrideBytes = 7 * mBytesPerFloat;
/** Offset of the position data. */
private final int mPositionOffset = 0;
/** Size of the position data in elements. */
private final int mPositionDataSize = 3;
/** Offset of the color data. */
private final int mColorOffset = 3;
/** Size of the color data in elements. */
private final int mColorDataSize = 4;
private float x;
/**
* Initialize the model data.
*/
public LessonOneRenderer()
{
// Define points for equilateral triangles.
// This triangle is white_blue.First sail is mainsail
final float[] triangle1VerticesData = {
// X, Y, Z,
// R, G, B, A
-0.5f, -0.25f, 0.0f,
1.0f, 1.0f, 1.0f, 1.0f,
0.0f, -0.25f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f,
0.0f, 0.56f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f};
// This triangle is white_blue..The second is called the jib sail
final float[] triangle2VerticesData = {
// X, Y, Z,
// R, G, B, A
-0.25f, -0.25f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f,
0.03f, -0.25f, 0.0f,
1.0f, 1.0f, 1.0f, 1.0f,
-0.25f, 0.4f, 0.0f,
0.8f, 0.8f, 1.0f, 1.0f};
// This triangle3 is blue.
final float[] triangle3VerticesData = {
// X, Y, Z,
// R, G, B, A
-1.0f, -1.5f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
1.0f, -0.35f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
-1.0f, -0.35f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f};
// This triangle4 is blue.
final float[] triangle4VerticesData = {
// X, Y, Z,
// R, G, B, A
-1.0f, -1.5f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
1.0f, -1.5f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
1.0f, -0.35f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f};
// This triangle5 is brown.
final float[] triangle5VerticesData = {
// X, Y, Z,
// R, G, B, A
-0.4f, -0.3f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f,
-0.4f, -0.4f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f,
0.3f, -0.3f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f};
// This triangle6 is brown.
final float[] triangle6VerticesData = {
// X, Y, Z,
// R, G, B, A
-0.4f, -0.4f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f,
0.22f, -0.4f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f,
0.3f, -0.3f, 0.0f,
0.7f, 0.3f, 0.4f, 1.0f};
// Initialize the buffers.
mTriangle1Vertices = ByteBuffer.allocateDirect(triangle1VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle2Vertices = ByteBuffer.allocateDirect(triangle2VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle3Vertices = ByteBuffer.allocateDirect(triangle3VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle4Vertices = ByteBuffer.allocateDirect(triangle4VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle5Vertices = ByteBuffer.allocateDirect(triangle5VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle6Vertices = ByteBuffer.allocateDirect(triangle6VerticesData.length * mBytesPerFloat)
.order(ByteOrder.nativeOrder()).asFloatBuffer();
mTriangle1Vertices.put(triangle1VerticesData).position(0);
mTriangle2Vertices.put(triangle2VerticesData).position(0);
mTriangle3Vertices.put(triangle3VerticesData).position(0);
mTriangle4Vertices.put(triangle4VerticesData).position(0);
mTriangle5Vertices.put(triangle5VerticesData).position(0);
mTriangle6Vertices.put(triangle6VerticesData).position(0);
}
@Override
public void onSurfaceCreated(GL10 glUnused, EGLConfig config)
{
// Set the background clear color to gray.
GLES20.glClearColor(0.5f, 0.5f, 0.7f, 1.0f);
// Position the eye behind the origin.
final float eyeX = 0.0f;
final float eyeY = 0.0f;
final float eyeZ = 1.5f;
// We are looking toward the distance
final float lookX = 0.0f;
final float lookY = 0.0f;
final float lookZ = -5.0f;
// Set our up vector. This is where our head would be pointing were we holding the camera.
final float upX = 0.0f;
final float upY = 1.0f;
final float upZ = 0.0f;
// Set the view matrix. This matrix can be said to represent the camera position.
// NOTE: In OpenGL 1, a ModelView matrix is used, which is a combination of a model and
// view matrix. In OpenGL 2, we can keep track of these matrices separately if we choose.
Matrix.setLookAtM(mViewMatrix, 0, eyeX, eyeY, eyeZ, lookX, lookY, lookZ, upX, upY, upZ);
final String vertexShader =
"uniform mat4 u_MVPMatrix; \n" // A constant representing the combined model/view/projection matrix.
+ "attribute vec4 a_Position; \n" // Per-vertex position information we will pass in.
+ "attribute vec4 a_Color; \n" // Per-vertex color information we will pass in.
+ "varying vec4 v_Color; \n" // This will be passed into the fragment shader.
+ "void main() \n" // The entry point for our vertex shader.
+ "{ \n"
+ " v_Color = a_Color; \n" // Pass the color through to the fragment shader.
// It will be interpolated across the triangle.
+ " gl_Position = u_MVPMatrix \n" // gl_Position is a special variable used to store the final position.
+ " * a_Position; \n" // Multiply the vertex by the matrix to get the final point in
+ "} \n"; // normalized screen coordinates.
final String fragmentShader =
"precision mediump float; \n" // Set the default precision to medium. We don't need as high of a
// precision in the fragment shader.
+ "varying vec4 v_Color; \n" // This is the color from the vertex shader interpolated across the
// triangle per fragment.
+ "void main() \n" // The entry point for our fragment shader.
+ "{ \n"
+ " gl_FragColor = v_Color; \n" // Pass the color directly through the pipeline.
+ "} \n";
// Load in the vertex shader.
int vertexShaderHandle = GLES20.glCreateShader(GLES20.GL_VERTEX_SHADER);
if (vertexShaderHandle != 0)
{
// Pass in the shader source.
GLES20.glShaderSource(vertexShaderHandle, vertexShader);
// Compile the shader.
GLES20.glCompileShader(vertexShaderHandle);
// Get the compilation status.
final int[] compileStatus = new int[1];
GLES20.glGetShaderiv(vertexShaderHandle, GLES20.GL_COMPILE_STATUS, compileStatus, 0);
// If the compilation failed, delete the shader.
if (compileStatus[0] == 0)
{
GLES20.glDeleteShader(vertexShaderHandle);
vertexShaderHandle = 0;
}
}
if (vertexShaderHandle == 0)
{
throw new RuntimeException("Error creating vertex shader.");
}
// Load in the fragment shader shader.
int fragmentShaderHandle = GLES20.glCreateShader(GLES20.GL_FRAGMENT_SHADER);
if (fragmentShaderHandle != 0)
{
// Pass in the shader source.
GLES20.glShaderSource(fragmentShaderHandle, fragmentShader);
// Compile the shader.
GLES20.glCompileShader(fragmentShaderHandle);
// Get the compilation status.
final int[] compileStatus = new int[1];
GLES20.glGetShaderiv(fragmentShaderHandle, GLES20.GL_COMPILE_STATUS, compileStatus, 0);
// If the compilation failed, delete the shader.
if (compileStatus[0] == 0)
{
GLES20.glDeleteShader(fragmentShaderHandle);
fragmentShaderHandle = 0;
}
}
if (fragmentShaderHandle == 0)
{
throw new RuntimeException("Error creating fragment shader.");
}
// Create a program object and store the handle to it.
int programHandle = GLES20.glCreateProgram();
if (programHandle != 0)
{
// Bind the vertex shader to the program.
GLES20.glAttachShader(programHandle, vertexShaderHandle);
// Bind the fragment shader to the program.
GLES20.glAttachShader(programHandle, fragmentShaderHandle);
// Bind attributes
GLES20.glBindAttribLocation(programHandle, 0, "a_Position");
GLES20.glBindAttribLocation(programHandle, 1, "a_Color");
// Link the two shaders together into a program.
GLES20.glLinkProgram(programHandle);
// Get the link status.
final int[] linkStatus = new int[1];
GLES20.glGetProgramiv(programHandle, GLES20.GL_LINK_STATUS, linkStatus, 0);
// If the link failed, delete the program.
if (linkStatus[0] == 0)
{
GLES20.glDeleteProgram(programHandle);
programHandle = 0;
}
}
if (programHandle == 0)
{
throw new RuntimeException("Error creating program.");
}
// Set program handles. These will later be used to pass in values to the program.
mMVPMatrixHandle = GLES20.glGetUniformLocation(programHandle, "u_MVPMatrix");
mPositionHandle = GLES20.glGetAttribLocation(programHandle, "a_Position");
mColorHandle = GLES20.glGetAttribLocation(programHandle, "a_Color");
// Tell OpenGL to use this program when rendering.
GLES20.glUseProgram(programHandle);
}
@Override
public void onSurfaceChanged(GL10 glUnused, int width, int height)
{
// Set the OpenGL viewport to the same size as the surface.
GLES20.glViewport(0, 0, width, height);
// Create a new perspective projection matrix. The height will stay the same
// while the width will vary as per aspect ratio.
final float ratio = (float) width / height;
final float left = -ratio;
final float right = ratio;
final float bottom = -1.0f;
final float top = 1.0f;
final float near = 1.0f;
final float far = 10.0f;
Matrix.frustumM(mProjectionMatrix, 0, left, right, bottom, top, near, far);
}
@Override
public void onDrawFrame(GL10 glUnused)
{
GLES20.glClear(GLES20.GL_DEPTH_BUFFER_BIT | GLES20.GL_COLOR_BUFFER_BIT);
// Draw the triangle facing straight on.
Matrix.setIdentityM(mModelMatrix, 0);
Matrix.translateM(mModelMatrix, 0, x, 0.0f, 0.0f);
drawTriangle(mTriangle1Vertices);
// Draw triangle_2.
Matrix.setIdentityM(mModelMatrix, 0);
Matrix.translateM(mModelMatrix, 0, x + 0.3f, 0.0f, 0.0f);
drawTriangle(mTriangle2Vertices);
if(x<=1){x = (float) (x + 0.001);}
else {x=0;}
// Draw triangle_3.
Matrix.setIdentityM(mModelMatrix, 0);
drawTriangle(mTriangle3Vertices);
// Draw triangle_4.
Matrix.setIdentityM(mModelMatrix, 0);
drawTriangle(mTriangle4Vertices);
// Draw triangle_5. Boat
Matrix.setIdentityM(mModelMatrix, 0);
Matrix.translateM(mModelMatrix, 0, x, 0.0f, 0.0f);
//Matrix.rotateM(mModelMatrix, 0, 0, 0.0f, 0.0f, 1.0f);
drawTriangle(mTriangle5Vertices);
// Draw triangle_6. Boat
Matrix.setIdentityM(mModelMatrix, 0);
Matrix.translateM(mModelMatrix, 0, x, 0.0f, 0.0f);
//Matrix.rotateM(mModelMatrix, 0, 0, 0.0f, 0.0f, 1.0f);
drawTriangle(mTriangle6Vertices);
}
/**
* Draws a triangle from the given vertex data.
*
* @param aTriangleBuffer The buffer containing the vertex data.
*/
private void drawTriangle(final FloatBuffer aTriangleBuffer)
{
// Pass in the position information
aTriangleBuffer.position(mPositionOffset);
GLES20.glVertexAttribPointer(mPositionHandle, mPositionDataSize, GLES20.GL_FLOAT, false,
mStrideBytes, aTriangleBuffer);
GLES20.glEnableVertexAttribArray(mPositionHandle);
// Pass in the color information
aTriangleBuffer.position(mColorOffset);
GLES20.glVertexAttribPointer(mColorHandle, mColorDataSize, GLES20.GL_FLOAT, false,
mStrideBytes, aTriangleBuffer);
GLES20.glEnableVertexAttribArray(mColorHandle);
// This multiplies the view matrix by the model matrix, and stores the result in the MVP matrix
// (which currently contains model * view).
Matrix.multiplyMM(mMVPMatrix, 0, mViewMatrix, 0, mModelMatrix, 0);
// This multiplies the modelview matrix by the projection matrix, and stores the result in the MVP matrix
// (which now contains model * view * projection).
Matrix.multiplyMM(mMVPMatrix, 0, mProjectionMatrix, 0, mMVPMatrix, 0);
GLES20.glUniformMatrix4fv(mMVPMatrixHandle, 1, false, mMVPMatrix, 0);
GLES20.glDrawArrays(GLES20.GL_TRIANGLES, 0, 3);
}
}
Список источников
1. Сатия Коматинени, Дэйв Маклин, Саид Хашими. Android 3 для профессионалов. Создание приложений для планшетных компьютеров и смартфонов.: Пер. с англ. – М.: ООО «И.Д.Вильямс». 2012 – 1024 с.
2. http://www.learnopengles.com/android-lesson-one-getting-started/
3. http://andmonahov.blogspot.com/2012/10/opengl-es-20-1.html
4. https://www.opengl.org/sdk/docs/tutorials/ClockworkCoders/attributes.php
5. https://www.khronos.org/opengles/sdk/docs/reference_cards/OpenGL-ES-2_0-Reference-card.pdf
Поделиться с друзьями


shape
Простыня исходников в публикации уводит все объяснения увлекательной математики в дальний и темный угол. Может стоит спрятать их под кат?
AlwaysDream
Согласен