Недавно на Хабре появилась публикация про алгоритм Хо-Кашьяпа (Ho-Kashyap procedure, он же — алгоритм НСКО, наименьшей среднеквадратичной ошибки). Мне она показалась не очень понятной и я решил разобраться в теме сам. Выяснилось, что в русскоязычном интернете тема не очень хорошо разобрана, поэтому я решил оформить статью по итогам поисков.
Несмотря на бум нейросетей в машинном обучении, алгоритмы линейной классификации остаются гораздо более простыми в использовании и интерпретации. Но при этом иногда вовсе не хочется пользоваться сколько-нибудь продвинутыми методами, вроде метода опорных векторов или логистической регрессии и возникает искушение загнать все данные в одну большую линейную МНК-регрессию, тем более её прекрасно умеет строить даже MS Excel.
Проблема такого подхода в том, что даже если входные данные линейно разделимы, то получившийся классификатор может их не разделять. Например, для набора точек![X = [(6, 9), (5, 7), (5, 9), (10, 1)]](https://tex.s2cms.ru/svg/%20X%20%3D%20%5B(6%2C%209)%2C%20(5%2C%207)%2C%20(5%2C%209)%2C%20(10%2C%201)%5D%20) ,
, ![y = [1, 1, -1, -1]](https://tex.s2cms.ru/svg/%20y%20%3D%20%5B1%2C%201%2C%20-1%2C%20-1%5D%20) получим разделяющую прямую
получим разделяющую прямую %20%3D%200%20) (пример позаимствован из (1)):
(пример позаимствован из (1)):
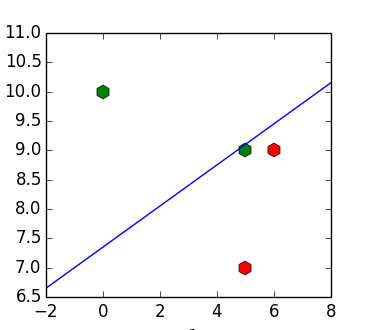
Встаёт вопрос — можно ли как-то избавиться от этой особенности поведения?
Для начала формализуем предмет статьи.
Дана матрица , каждая строчка
, каждая строчка  которой соответствует признаковому описанию объекта
которой соответствует признаковому описанию объекта  (включая константу
(включая константу  ) и вектора меток классов
) и вектора меток классов  , где
, где  — метка объекта
— метка объекта  . Мы хотим построить линейный классификатор вида
. Мы хотим построить линейный классификатор вида %20%3D%20y%20) .
.
Самый простой способ это сделать — построить МНК-регрессию для , то есть минимизировать сумму квадратов отклонений
, то есть минимизировать сумму квадратов отклонений %5E2%20) . Оптимальные веса можно найти по формуле
. Оптимальные веса можно найти по формуле  , где
, где  — псевдообратная матрица. Таким образом получена картинка из начала статьи.
— псевдообратная матрица. Таким образом получена картинка из начала статьи.
Для удобства записи мы поэлементно домножим каждую строчку неравенства на
на  и назовём получившуюся в левой части матрицу
и назовём получившуюся в левой части матрицу  (здесь
(здесь  означает построчное умножение). Тогда условие для МНК-регрессии сведётся к виду
означает построчное умножение). Тогда условие для МНК-регрессии сведётся к виду  , а задача минимизации — к минимизации
, а задача минимизации — к минимизации %5E2%20) .
.
На этом месте можно вспомнить, что условие разделения классов это%20%3D%20y%20) или
или %20%3D%201%20) , и поскольку мы хотим разделять классы, то надо решать эту задачу.
, и поскольку мы хотим разделять классы, то надо решать эту задачу.
Введём вектор , в котором
, в котором  отвечает за расстояние от элемента
отвечает за расстояние от элемента  до разделяющей прямой (
до разделяющей прямой ( ). Поскольку мы хотим, чтобы все элементы были классифицированы правильно, мы вводим условие
). Поскольку мы хотим, чтобы все элементы были классифицированы правильно, мы вводим условие  . Тогда задача сведётся к
. Тогда задача сведётся к %5E2%20) и будет решаться как
и будет решаться как  . Можно вручную подобрать такие значения
. Можно вручную подобрать такие значения  , что получившаяся плоскость будет разделять нашу выборку:
, что получившаяся плоскость будет разделять нашу выборку:
Алгоритм Хо-Кашьяпа предназначен для того, чтобы подобрать автоматически. Схема алгоритма (
автоматически. Схема алгоритма ( — номер шага,
— номер шага, %7D%20) обычно берут равным
обычно берут равным  ):
):
Вектор отступов хочется вычислить каким-нибудь путём вроде%7D%20%3D%20%5Cmax(Yw%5E%7B(k)%7D%2C%200)%20) , поскольку это минимизирует функцию потерь
, поскольку это минимизирует функцию потерь %5E2%20) . К сожалению, условие
. К сожалению, условие  не даёт нам этого сделать, и вместо этого предлагается делать шаг по положительной части градиента функции потерь
не даёт нам этого сделать, и вместо этого предлагается делать шаг по положительной части градиента функции потерь %7D%20%3D%20b%5E%7Bk%7D%20-%20Yw%5E%7B(k)%7D%20) :
: %7D%20%3D%20b%5E%7B(k)%7D%20-%20%5Cmu%20(e%5E%7B(k)%7D%20-%20%7Ce%5E%7Bk%7D%7C)%20) , где
, где  — шаг градиентного спуска, уменьшающийся по ходу решения задачи.
— шаг градиентного спуска, уменьшающийся по ходу решения задачи.
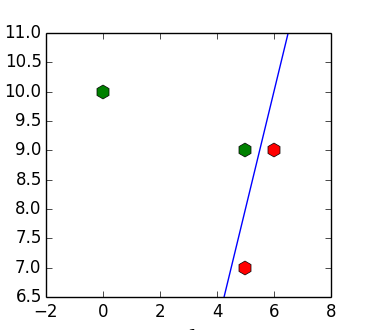
В случае линейно-разделимой выборки алгоритм всегда сходится и сходится к разделяющей плоскости (если все элементы градиента по неотрицательны, то они все нулевые).
неотрицательны, то они все нулевые).
В случае линейно-неразделимой выборки, функция потерь может быть сколь угодно малой, поскольку достаточно домножить и
и  на константу для изменения её значения и в принципе алгоритм может и не сойтись. Поиск не даёт никаких конкретных рекомендаций на эту тему.
на константу для изменения её значения и в принципе алгоритм может и не сойтись. Поиск не даёт никаких конкретных рекомендаций на эту тему.
Можно заметить, что если объект классифицирован правильно, то ошибка в поставленной оптимизационной задаче (%5E2%20) ) ошибка на нём может быть сведена к нулю. Если же объект классифицирован неправильно, то минимальная ошибка на нём равна квадрату его отступа от разделяющей прямой (
) ошибка на нём может быть сведена к нулю. Если же объект классифицирован неправильно, то минимальная ошибка на нём равна квадрату его отступа от разделяющей прямой (%5E2%20) ). Тогда функцию потерь можно переписать в виде:
). Тогда функцию потерь можно переписать в виде:
%5E2%20-%202%5Cmax(0%2C%201%20-%20w%20Y_i)%20%20)
В свою очередь, функция потерь линейного SVM имеет вид:
%20)
Таким образом, задача, решаемая алгоритмом Хо-Кашьяпа, представляет собой некоторый аналог SVM с квадратичной функцией потерь (она сильнее штрафует за выбросы далеко от разделяющей плоскости) и игнорирующий ширину разделяющей полосы (т.е. ищущий не плоскость, находящуюся максимально далеко от ближайших правильно классифицированных элементов, а любую разделяющую плоскость).
Можно вспомнить, что МНК-регрессия является аналогом двухклассового линейного дискриминанта Фишера (их решения совпадают с точностью до константы). Алгоритм Хо-Кашьпяпа можно применить и для случая классов — в этом
классов — в этом  и
и  становятся матрицами
становятся матрицами  и
и  размера
размера  и
и  соотвественно, где
соотвественно, где  — размерность задачи, а
— размерность задачи, а  — число объектов. В этом случае в столбцах, соответствующих неверным классам, должны стоять отрицательные значения.
— число объектов. В этом случае в столбцах, соответствующих неверным классам, должны стоять отрицательные значения.
parpalak за удобный редактор.
rocket3 за оригинальную статью.
Несмотря на бум нейросетей в машинном обучении, алгоритмы линейной классификации остаются гораздо более простыми в использовании и интерпретации. Но при этом иногда вовсе не хочется пользоваться сколько-нибудь продвинутыми методами, вроде метода опорных векторов или логистической регрессии и возникает искушение загнать все данные в одну большую линейную МНК-регрессию, тем более её прекрасно умеет строить даже MS Excel.
Проблема такого подхода в том, что даже если входные данные линейно разделимы, то получившийся классификатор может их не разделять. Например, для набора точек

Встаёт вопрос — можно ли как-то избавиться от этой особенности поведения?
Задача линейной классификации
Для начала формализуем предмет статьи.
Дана матрица
>>> import numpy as np
>>> X = np.array([[6, 9, 1], [5, 7, 1], [5, 9, 1], [0, 10, 1]])
>>> y = np.array([[1], [1], [-1], [-1]])
Самый простой способ это сделать — построить МНК-регрессию для
>>> w = np.dot(np.linalg.pinv(X), y)
>>> w
array([[ 0.15328467],
[-0.4379562 ],
[ 3.2189781 ]])
>>> np.dot(X, w)
array([[ 0.19708029],
[ 0.91970803],
[ 0.04379562],
[-1.16058394]])
Линейная разделимость
Для удобства записи мы поэлементно домножим каждую строчку неравенства
>>> Y = y * X
>>> Y
array([[ 6, 9, 1],
[ 5, 7, 1],
[ -5, -9, -1],
[ 0, -10, -1]])
На этом месте можно вспомнить, что условие разделения классов это
Введём вектор
>>> b = np.ones([4, 1])
>>> b[3] = 10
>>> w = np.dot(np.linalg.pinv(Y), b)
>>> np.dot(Y, w)
array([[ 0.8540146 ],
[ 0.98540146],
[ 0.81021898],
[ 10.02919708]])
Алгоритм Хо-Кашьяпа
Алгоритм Хо-Кашьяпа предназначен для того, чтобы подобрать
- Вычислить коэффициенты МНК-регрессии (
).
- Вычислить вектор отступов
.
- Если решение не сошлось (
), то повторить шаг 1.
Вектор отступов хочется вычислить каким-нибудь путём вроде
>>> e = -np.inf * np.ones([4, 1])
>>> b = np.ones([4, 1])
>>> while np.any(e < 0):
... w = np.dot(np.linalg.pinv(Y), b)
... e = b - np.dot(Y, w)
... b = b - e * (e < 0)
...
>>> b
array([[ 1.],
[ 1.],
[ 1.],
[ 12.]])
>>> w
array([[ 2.],
[-1.],
[-2.]])

В случае линейно-разделимой выборки алгоритм всегда сходится и сходится к разделяющей плоскости (если все элементы градиента по
В случае линейно-неразделимой выборки, функция потерь может быть сколь угодно малой, поскольку достаточно домножить
Связь алгоритма Хо-Кашьяпа и линейного SVM
Можно заметить, что если объект классифицирован правильно, то ошибка в поставленной оптимизационной задаче (
В свою очередь, функция потерь линейного SVM имеет вид:
Таким образом, задача, решаемая алгоритмом Хо-Кашьяпа, представляет собой некоторый аналог SVM с квадратичной функцией потерь (она сильнее штрафует за выбросы далеко от разделяющей плоскости) и игнорирующий ширину разделяющей полосы (т.е. ищущий не плоскость, находящуюся максимально далеко от ближайших правильно классифицированных элементов, а любую разделяющую плоскость).
Многомерный случай
Можно вспомнить, что МНК-регрессия является аналогом двухклассового линейного дискриминанта Фишера (их решения совпадают с точностью до константы). Алгоритм Хо-Кашьпяпа можно применить и для случая
Благодарности
parpalak за удобный редактор.
rocket3 за оригинальную статью.
Ссылки
(1) http://www.csd.uwo.ca/~olga/Courses/CS434a_541a/Lecture10.pdf
(2) http://research.cs.tamu.edu/prism/lectures/pr/pr_l17.pdf
(3) http://web.khu.ac.kr/~tskim/PatternClass Lec Note 07-1.pdf
(4) А.Е. Лепский, А.Г. Броневич Математические методы распознавания образов. Курс лекций
(5) Ту Дж., Гонсалес Р. Принципы распознавания образов
(6) Р.Дуда, П.Харт Распознавание образов и анализ сцен
Поделиться с друзьями


Dark_Daiver
>Таким образом, задача, решаемая алгоритмом Хо-Кашьяпа, представляет собой некоторый аналог SVM с квадратичной функцией потерь
Я бы добавил, что при наличии нескольких гиперплоскостей для линейно разделимого случая SVM выберет наиболее «среднюю» плоскость (за это отвечает терм lambda * ||w||^2). В случае алгоритма Хо-Кашьяпа этого (если я все правильно понял), не происходит. На мой взгляд это довольно важно.
Drino
Добавил примечание про ширину разделяющей полосы. Спасибо!