
Привет друзья! Будучи студентами одного небезызвестного образовательного проекта, мы с bo_0m, после вводной лекции по курсу Углубленное программирование на Java, получили свое первое домашнее задание. Необходимо было реализовать программу, которая бы перемножала матрицы. И всё бы ничего, да так совпало, что на следующей неделе должна была состояться конференция Joker, и наш преподаватель решил отменить по такому случаю занятие, подарив нам несколько часов свободного пятничного вечера. Не пропадать же времени зря! Раз никто не торопит, то можно подойти к делу творчески.
Welcome, under the hood v
Первое, что приходит в голову
Наверно каждому студенту технического вуза приходилось перемножать матрицы. Алгоритм был всегда один, а именно, простенький кубический метод перемножения. Да и как бы это ни звучало, но данный способ не так-то уж и плох (для размерностей матриц меньше 100).
Все мы с этого начинали:
for (int i = 0; i < A.rows(); i++) {
for (int j = 0; j < B.columns(); j++) {
for (int k = 0; k < A.columns(); k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
Забегая вперед, скажу, что мы будем использовать модифицированный вариант с применением транспонирования. Про такую модификацию хорошо написано здесь, да и не только про неё.
Окей, поехали дальше!
Алгоритм Штрассена
Возможно, не все знают, но автор алгоритма Фолькер Штрассен не только жив, но и активно преподает, так же являясь почетным профессором кафедры математики и статистики Констанцского университета. Обязательно почитайте про этого человека хотя бы на вики.
Немножко теории из Википедии:
Пусть A и B — две (n*n)-матрицы, причём n — степень числа 2. Тогда можно разбить каждую матрицу A и B на четыре ((n/2)*(n/2))-матрицы и через них выразить произведение матриц A и B:
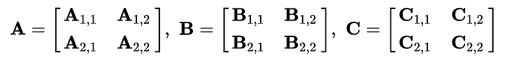
Определим новые элементы:
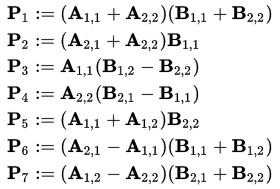
Таким образом, нам нужно всего 7 умножений на каждом этапе рекурсии. Элементы матрицы C выражаются из Pk по формулам:
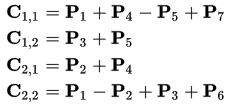
Рекурсивный процесс продолжается n раз, до тех пор пока размер матриц Ci,j не станет достаточно малым, далее используют обычный метод умножения матриц. Это делают из-за того, что алгоритм Штрассена теряет эффективность по сравнению с обычным на малых матрицах в силу большего числа сложений.
let's go to practice!
Для реализации алгоритма Штрассена нам понадобятся дополнительные функции. Как было сказано выше, алгоритм работает только с квадратными матрицами, размерность которых равна степени 2, поэтому приведем исходные матрицы к такому виду.
Для этого была реализована функция, которая определяет новую размерность:
private static int log2(int x) {
int result = 1;
while ((x >>= 1) != 0) result++;
return result;
}
//******************************************************************************************
private static int getNewDimension(int[][] a, int[][] b) {
return 1 << log2(Collections.max(Arrays.asList(a.length, a[0].length, b[0].length)));
// Л - Лаконично
}
И функция, которая расширяет матрицу до нужного размера:
private static int[][] addition2SquareMatrix(int[][] a, int n) {
int[][] result = new int[n][n];
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a[i].length; j++) {
result[i][j] = a[i][j];
}
}
return result;
}
Теперь исходные матрицы удовлетворяют требованиям для реализации алгоритма Штрассена. Также нам понадобится функция, которая позволит разбить матрицу размером n*n на четыре матрицы (n/2)*(n/2) и обратная для восстановления матрицы:
private static void splitMatrix(int[][] a, int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
int n = a.length >> 1;
for (int i = 0; i < n; i++) {
System.arraycopy(a[i], 0, a11[i], 0, n);
System.arraycopy(a[i], n, a12[i], 0, n);
System.arraycopy(a[i + n], 0, a21[i], 0, n);
System.arraycopy(a[i + n], n, a22[i], 0, n);
}
}
//******************************************************************************************
private static int[][] collectMatrix(int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
int n = a11.length;
int[][] a = new int[n << 1][n << 1];
for (int i = 0; i < n; i++) {
System.arraycopy(a11[i], 0, a[i], 0, n);
System.arraycopy(a12[i], 0, a[i], n, n);
System.arraycopy(a22[i], 0, a[i + n], n, n);
}
return a;
}
Вот мы и добрались до самого интересного, основная функция перемножения матриц алгоритмом Штрассена выглядит следующим образом:
private static int[][] multiStrassen(int[][] a, int[][] b, int n) {
if (n <= 64) {
return multiply(a, b);
}
n = n >> 1;
int[][] a11 = new int[n][n];
int[][] a12 = new int[n][n];
int[][] a21 = new int[n][n];
int[][] a22 = new int[n][n];
int[][] b11 = new int[n][n];
int[][] b12 = new int[n][n];
int[][] b21 = new int[n][n];
int[][] b22 = new int[n][n];
splitMatrix(a, a11, a12, a21, a22);
splitMatrix(b, b11, b12, b21, b22);
int[][] p1 = multiStrassen(summation(a11, a22), summation(b11, b22), n);
int[][] p2 = multiStrassen(summation(a21, a22), b11, n);
int[][] p3 = multiStrassen(a11, subtraction(b12, b22), n);
int[][] p4 = multiStrassen(a22, subtraction(b21, b11), n);
int[][] p5 = multiStrassen(summation(a11, a12), b22, n);
int[][] p6 = multiStrassen(subtraction(a21, a11), summation(b11, b12), n);
int[][] p7 = multiStrassen(subtraction(a12, a22), summation(b21, b22), n);
int[][] c11 = summation(summation(p1, p4), subtraction(p7, p5));
int[][] c12 = summation(p3, p5);
int[][] c21 = summation(p2, p4);
int[][] c22 = summation(subtraction(p1, p2), summation(p3, p6));
return collectMatrix(c11, c12, c21, c22);
}
На этом можно было бы и закончить. Реализованный алгоритм работает
Пора распараллелить
Java 7 предоставляет прекрасный API для распараллеливания рекурсивных задач. С её выходом появилось одно из дополнений к пакетам java.util.concurrent — реализация парадигмы Divide and Conquer — Fork-Join. Идея заключается в следующем: рекурсивно разбиваем задачу на подзадачи, решаем, а потом объединяем результаты. Более подробно с данной технологией можно ознакомиться в документации.
Посмотрим как легко и эффективно можно применить эту парадигму к нашему алгоритму Штрассена.
private static class myRecursiveTask extends RecursiveTask<int[][]> {
private static final long serialVersionUID = -433764214304695286L;
int n;
int[][] a;
int[][] b;
public myRecursiveTask(int[][] a, int[][] b, int n) {
this.a = a;
this.b = b;
this.n = n;
}
@Override
protected int[][] compute() {
if (n <= 64) {
return multiply(a, b);
}
n = n >> 1;
int[][] a11 = new int[n][n];
int[][] a12 = new int[n][n];
int[][] a21 = new int[n][n];
int[][] a22 = new int[n][n];
int[][] b11 = new int[n][n];
int[][] b12 = new int[n][n];
int[][] b21 = new int[n][n];
int[][] b22 = new int[n][n];
splitMatrix(a, a11, a12, a21, a22);
splitMatrix(b, b11, b12, b21, b22);
myRecursiveTask task_p1 = new myRecursiveTask(summation(a11,a22),summation(b11,b22),n);
myRecursiveTask task_p2 = new myRecursiveTask(summation(a21,a22),b11,n);
myRecursiveTask task_p3 = new myRecursiveTask(a11,subtraction(b12,b22),n);
myRecursiveTask task_p4 = new myRecursiveTask(a22,subtraction(b21,b11),n);
myRecursiveTask task_p5 = new myRecursiveTask(summation(a11,a12),b22,n);
myRecursiveTask task_p6 = new myRecursiveTask(subtraction(a21,a11),summation(b11,b12),n);
myRecursiveTask task_p7 = new myRecursiveTask(subtraction(a12,a22),summation(b21,b22),n);
task_p1.fork();
task_p2.fork();
task_p3.fork();
task_p4.fork();
task_p5.fork();
task_p6.fork();
task_p7.fork();
int[][] p1 = task_p1.join();
int[][] p2 = task_p2.join();
int[][] p3 = task_p3.join();
int[][] p4 = task_p4.join();
int[][] p5 = task_p5.join();
int[][] p6 = task_p6.join();
int[][] p7 = task_p7.join();
int[][] c11 = summation(summation(p1, p4), subtraction(p7, p5));
int[][] c12 = summation(p3, p5);
int[][] c21 = summation(p2, p4);
int[][] c22 = summation(subtraction(p1, p2), summation(p3, p6));
return collectMatrix(c11, c12, c21, c22);
}
}
Кульминация
Вам, наверно, уже не терпится посмотреть на сравнение производительности работы алгоритмов на реальном железе. Сразу оговорим, что тестирование будем проводить на квадратных матрицах. Итак, мы имеем:
- Традиционный (Кубический) метод умножения матриц
- Традиционный с применением транспонирования
- Алгоритм Штрассена
- Распараллеленный алгоритм Штрассена
Размерность матриц будем задавать в интервале [100..4000] и с шагом в 100.
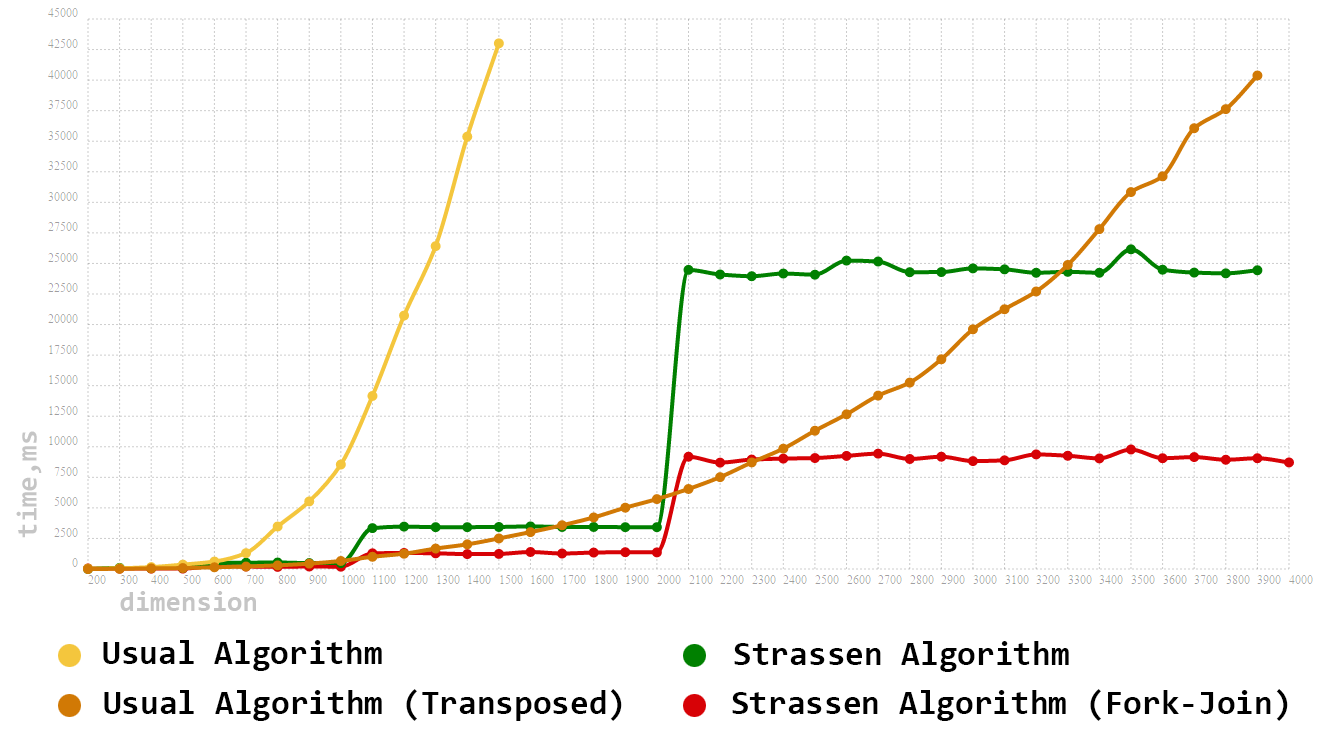
Как и ожидалось, наш первый алгоритм сразу выпал из тройки лидеров. Но вот с его модернизированным братом(вариант с транспонированием) не все так просто. Даже на довольно больших размерностях данный алгоритм не только не уступает, но и зачастую превосходит однопоточный алгоритм Штрассена. И всё же, имея в рукаве козырь в виде Fork-Join Framework'а, нам удалось получить весомый прирост производительности. Распараллеливание алгоритма Штрассена позволило сократить время перемножения почти в 3 раза, а также возглавить наш итоговый тотал.
» Исходный код размещен здесь.
Будем рады отзывам и замечаниям к нашей работе. Спасибо за внимание!
Комментарии (28)
vlanko
21.10.2016 23:341) в отличие от старой статьи не указан процессор — количесто ядер? :)
2) почему при удвоении задачи (скачек степени двойки, как я понимаю?) время растет в 7 раз?
7 умножений, но непонятна функция роста.
jfalko
21.10.2016 23:421. Тестировалось все на обычных ноутбуках c i5-i7 и 6gb оперативной памяти(ноутам 3-4 года).
2. Да вы всё правильно понимаете, дело в том, что да, дело в степени двойки:)… Алгоритм работает с квадратными матрицами и из сего следует, что при размерах в 1025*1025 матрица увеличивается до 2048*2048, так же если размер матрицы 1500*1500, то матрица всё также увеличивается до размерности в 2048. Вот и происходит 7 кратный взрыв при переходе с одной степени 2 к другой. И в общем случае получается, что переумножать матрицы размером, например, в 1200*1200 и 2000*2000 — нет, просто нет.(при расширении она дополняется нулями)
Спасибо за комментарий и обратную связь!
jfalko
21.10.2016 23:55*Опечатался*
И в общем случае получается, что переумножать матрицы размером, например, в 1200*1200 и 2000*2000 — нет, просто нет Разницы, они расширяются до 2048.

smile616
22.10.2016 00:00А что если дать каждому алгоритму перемножать N наборов матриц, где N кратно числу ядер на машине? Тогда можно будет сделать и сравнить параллельную версию Usual Algorithm (Transposed) с Stassen Algorithm Fork-Join. А вдруг он всё же лучше?

jfalko
22.10.2016 00:06Что Вы понимаете под набором матриц?
В каждом тесте работа велась только с одной матрицей определенной размерности. Дальше матрицы с шагом в 100 увеличивали свою размерность. Алгоритм Штрассена выделяет подматрицы и каждую такую подматрицу можно и нужно расспараллеливать на вычисление. А вот как выделить подматрицы в обычном алгоритме и можно ли это в принципе… я лично не знаю(отношусь скептически):)
ALLIGATOR
22.10.2016 17:24Я понял комментарий smile616 как то, что алгоритм Штрассена будучи выполняемым на 8 ядрах начинает опережать вариант с транспонированием выполняющийся на 1 ядре. Но разница далеко не приближается к 8. И что будет интересно замерять время выполнения двух алгоритмов перемножая матрицы не один раз, а как минимум 8 раз. Так, чтобы алгоритм транспонирования был запущен в 8-ми тредах, обрабатывая каждый свою матрицу.

Deosis
22.10.2016 12:16Прочитал метод сборки матриц и вспомнил анекдот про индейцев:
А на третий день Зоркий Глаз заметил, что четвёртой стены нет.
Насчёт транспонирования, это позволяет использовать кэш процессора намного эффективнее.
В вашей реализации идут постоянные копирования, из-за этого сильно проседает производительность.
ПС: Диаграмма обрывается прямо перед скачком, что не всем очевидно.
jfalko
22.10.2016 13:41Траспонирование — это не какой-то magic. Оно нужно сугубо для Java, это её особенность чтения массивов. На других языках (например: Fortran) вообще не потребуется никого траспонировать.
Предложите вариант без копирования. Вообще нативное копирование работает очень даже быстро. Тому пример ArrayList, который даже с копирование в среднем случае работает быстрей LinkedList'а.
Скачки видны до этого, а если бы мы их добавили, то сложно было бы смаштабировать результаты в читабельный график (Да и памяти у нас под Штрассена не много).
entomolog
23.10.2016 05:07Траспонирование — это не какой-то magic. Оно нужно сугубо для Java, это её особенность чтения массивов. На других языках (например: Fortran) вообще не потребуется никого траспонировать.
Deosis правильно написал, что транспонирование позволяет эффективнее использовать кэш, а вы говорите про какой-то «magic». Это не особенность Java, это особенность хранения двумерного массива в линейном адрессном пространстве. И в Fortran будет то-же самое, с той лишь разницей, что транспонирование там нужно будет делать иначе, так как двумерные массивы там хранятся column-wise, а не row-wise как в большинстве языков, где есть двумерные массивы.
jfalko
23.10.2016 13:05Примечательно, что Fortran не имеет такой проблемы. Многомерные массивы в нем хранятся по столбцам. Поэтому, кеш будет эксплуатироваться как следует и штатная реализация кубического алгоритма будет работать в разы быстрее.
В нашей статье есть ссылка на другую хабра-статью с траспонированием и там сказано, что в Фортране не потребуется делать траспонирование и обычный алгоритм будет работать в разы быстрей и кэшем всё тоже ок.
Спасибо за Ваш интерес!)
P.S. «magic» я упомянул с иронией, не более
entomolog
24.10.2016 03:32То, что там так сказано, не значит, что так оно и есть. В той статье есть комментарий по этому поводу.
Дело в том, что column-wise ни чем не лучше row-wise, это абсолютно симметричные способы хранения матриц. Поэтому column-wise не может быть лучше или хуже для перемножения.
Для нематематических приложений, row-wise удобнее, для математических column-wise удобнее.
Мысль, которую я пытался донести, это то, что это никакая не «особенность Java». И в Fortran проблема будет точно такая же. Не во всех ЯП есть многомерные массивы, вот в С/C++ нет. Но сам факт того, что двумерный массив хранится в линейном адрессном пространстве, вызывает cache miss при перемножении, и неважно как мы выбрали хранить массивы column-wise или row-wise.
Посмотрите на тело самого внутреннего цикла:
C[i][j] += A[i][k] * B[k][j];
Здесь, внутренний цикл инкрементирует переменную k. Доступ к элементам матрицы A не вызывает cache miss, так как A[i][k] и A[i][k+1] находятся «рядом», но есть проблема с B, так как элементы B[k][j] и B[k+1][j] находятся «далеко». Поэтому трансонирование матрицы B так сильно улучшает результат.
Теперь представим, что у нас Fortran, и матрицы хранятся column-wise. В этом случае элементы B[k][j] и B[k+1][j] находятся «рядом» и матрицу B транспонировать не нужно, однако A[i][k] и A[i][k+1] находятся «далеко» и теперь уже доступ к ним будет вызывать cache miss. Теперь транспонировать нужно матрицу A.
Что мы выиграли заменив row-wise на column-wise? Ничего.
P.S.
P.S. «magic» я упомянул с иронией, не более
Я понял вашу иронию, cache miss для меня никак не «magic», а объективная реальность, а вот загадочная «особенность Java» о которой вы говорили, как раз «magic».
vlanko
22.10.2016 13:09Я смотрю, транспонированный алгоритм имеет скорость роста 7,5-8 за удвоение. Но маленький коэффициент перед х^3
Штрасена — ровно 7. Так что в перспективе лучше даже без распаралеливанья. Но с какого момента гарантировано лучше?
jfalko
22.10.2016 13:35Гарантий я дать не могу. Но думаю, что асимптотически расспараллеленный Штрассен будет работать быстрей с точки зрения математики. На практике же существуют ограничения, например, из-за своей рекурсивной природы алгоритму требуется много памяти, и на предельных загрузках многое будет зависить от GC (Мы же всё таки говорим о реализации под JVM), да и число ядер у нас не бесконечное число т.д. и т.п… Поэтому не нужно считать это панацеей. В нашей случае, мы использовали средненькие по производительности ноутбуки с выделением 8 ядер и оперативной памяти порядка 4-6гб под jvm. GC работал на пределе. И ясно, что проверить реализации у нас не получится на матрицах размерностью 8_000 и более в силу ограничений на железо.

lany
23.10.2016 08:09log2
Integer.highestOneBit(x - 1) + 1?
log2(Collections.max(Arrays.asList(a.length, a[0].length, b[0].length)))
Integer.highestOneBit((a.length-1) | (a[0].length-1) | (b[0].length-1)) + 1— вроде так. Битовое или как раз вам сохранит старший установленный бит. Раз бьёмся за производительность, странно создавать список, объектный массив и боксинг-анбоксинг впихивать. Это один раз делается, конечно, но всё же.
Копирований, конечно, сильно много уж. Обычно подобные алгоритмы реализуют, выделяя кусок рабочей памяти один раз и используя из него соответствующие фрагменты. Тут даже в простой реализации, видимо, дополнительной памяти потребуется столько же, сколько исходная матрица. Так как у вас всё в степенях двойки, вычисление смещений будет быстро делаться с помощью битовых сдвигов. Ну и появится локальность, конечно.

jfalko
23.10.2016 13:24Вы правы. Так действительно будет быстрей, но на итоговую скорость работы всего алгоритма вряд ли повлияет. Зато код станет кратче.
Что касается копирования, да их тут много. Подобные алгоритмы в принципе решаются на других языка, где имеется соответсвующая гибкость работы с памятью. Мы же говорим про реализацию только на Java.
Спасибо за Ваши советы!
lany
23.10.2016 16:28Мы же говорим про реализацию только на Java
Ну это вы зря. Из того, что реализация только на Java, не значит, что её нельзя сделать быстрой. В данной задаче не нужна гибкость управления памятью. Языки вроде C/C++ могут выиграть здесь за счёт применения эффективных инструкций SSE (по факту реализация будет даже не на C/C++, а на ассемблере). Но особая гибкость памяти здесь не нужна, джавовское управление памятью никак не замедляет алгоритм, если правильно им воспользоваться.

jfalko
23.10.2016 21:27Из того, что реализация только на Java, не значит, что её нельзя сделать быстрой
А кто сказал, что реализация работает медленно?) Просто есть противоречия в словах. То память расходуется не правильно, то в джавовское управление памятью не замедляет алгоритм. Если есть конкретные идеи, то предлагайте. А то это перерастает в какой-то холивар)
lany
24.10.2016 06:12Эээ. Конкретная идея была в предыдущем комментарии. Может, я её непонятно сформулировал. Надо выделить буфер один раз и в нём жить, не выделять память много раз и не копировать. Кроме того выделить линейный массив, а не многомерный.

jfalko
24.10.2016 14:28Я, наверно, понял Вашу идею. Вы предлагаете в task'и передавать исходную матрицу и еще необходимые индиксы для того, чтобы выделять в исходной необходимые подматрицы. Хммм, да, скорее всего при грамотной реализации это даст существенный прирост производительности, но вот читаймость и ясность кода упадет в разы.( Тоже касается и с выделением линейного массива. Думаю, лучше выбор решения оставить за тем, кому оно понадобится. Всё таки приросты производительности будут на очень больших матрицах(На практике почти не встречаются). А для матриц меньше 500*500 лучше оставить код более легкий и краткий код.
Спасибо за Ваш интерес.
P.S. кст, Вы один из тех, из-за кого наш преподаватель отменил занятие(из-за Joker), так что, возможно, если бы не Вы, то этой статьи и не было бы:))

entomolog
24.10.2016 02:57У вас в простейшем кубическом методе перемножения ошибка.
При перемножении матрицы A размерностью mxn и матрицы B размерностью nxk, должна получаться матрица C размерностью mxk. Ваш алгоритм будет работать корректно только для квадратных матриц.
Ваш код:
for (int i = 0; i < A.rows(); i++) { for (int j = 0; j < A.columns(); j++) { for (int k = 0; k < B.columns(); k++) { C[i][j] += A[i][k] * B[k][j]; } } }
Если A.columns() > A.rows(), то будет выход за пределы индексов С (если конечно вы создали матрицу С правильно размера). И в самом внутреннем цикле, граница также неправильная.
По идее, должно быть что-то вроде:
for (int i = 0; i < A.rows(); i++) { for (int j = 0; j < B.columns(); j++) { for (int k = 0; k < A.columns(); k++) { C[i][j] += A[i][k] * B[k][j]; } } }
Ну и конечно где-то выше должна быть проверка, что A.columns() == B.rows(), но положим, что проверку мы здесь опускаем.
P.S. Я понимаю, что это было взято из другой статьи, но там хватает неточностей.
jfalko
24.10.2016 12:53Исправил! Даже стандарный пример взять нельзя:( Всё нужно перепроверять. Фразу с «особенностью» убрал.
В нашем исходном коде всё ок. Валидация проверит корректность размерностей матриц да и не только это.
Спасибо за такое внимание!


gbg
Теперь нужно сравнить с DGEMM из какой-нибудь хорошей реализации BLAS на CPU (ATLAS, MKL) или на GPU (ViennaCL) и поставить жирную точку в вопросе, «а кто ж быстрее-то?».
u_w
или сравнить с haskell реализацией.
jfalko
С хаскел не знакомы, если есть знания и желания, то можете смело брать нашу реализацию и сравнивать :)
Спасибо за отзыв)
jfalko
Всё же сравнивать с нативными отклаженными годами библиотеками будет не совсем корректно. Переписывать всё на С/С++ желания и времени, к сажалению, нет(
НО! Раз наша статья получила такой резонанс(Мы ожидали меньшего), то появилась идея обощить принципы решения подобных типов задач и, например, взять к и попробовать всё это дело на СКЦ(Суперкомпьютерном центре) Политехнического Университета СПб. Дело тут уже состоит в том, чтобы убедить высокопоставленных людей, что подобного рода задач интересны и важны, тогда получим доступ к очень серьёзным ресурсам. Надеюсь я Вы меня правильно поняли, большое спасибо за комментарий к нашей работе! :)
jfalko
к сожалению
Странно, что нет функционала по редактированию своих же комментариев( много опечаток
gbg
Как раз сравнить с нативной библиотекой — более чем корректно. Если для решения типовой задачи, для которой есть прекрасная (и с «хорошей» лицензией BSD) отмычка в виде ATLAS или ViennaCL, начинают лепить велосипед, нужно убедиться, что проигрыш будет хотя бы не драматическим.
Причем, написание велосипеда — это проигрыш на время самого написания и отладки (что быстрее, написать ваше или подцепить BLAS через JNI) и на скорость вычислений (ведь и на С++ можно написать так, что все колом встанет).