Всем привет, готов ещё один разбор. Сегодня будем смотреть доклад не с JPoint, а с DotNext! Автор доклада — Андрей DreamWalker Акиньшин, и посвящено его выступление деталям реализации арифметики с плавающей точкой в .NET:
Слайды можно найти здесь.
Дисклеймер: про реализацию арифметики только сам разбираемый доклад, а не собственно статья.
В этом месте нужно сказать, что я не очень люблю паззлеры. Они требуют знания покрытых мраком уголков спецификации, которое в реальной жизни обычно бесполезно. Просто представьте, что вы сопровождаете код, написанный любителем загадок.
Заметим, заставить человека самого подумать о чём-то важном, прежде чем рассказывать ему, «как правильно» — в общем случае хорошо, он гораздо лучше запомнит результат. Но начать с сути, то есть выбрать знание, которое нужно передать людям, и проиллюстрировать его парадоксальной задачей с простыми условиями — трудно. Для паззлеров часто проще взять те вещи, которые помнить не очень критично, зато их никто не знает, и сделать из них чистое развлечение.
В общем, внимательный читатель легко проследит в этой статье мою нелюбовь к жанру.
Нет ли тут противоречия: на сцену приходят помощники, чтобы создать иллюзию соревнования, но видно, что ответы и переходные реплики между задачами известны заранее. Например, на 12:00-12:20 Юля рассуждает о том, что приведение к целому — не та операция, и нужно использовать округление, и тут же появляется следующая задача, как раз на округление. Я бы в таких ситуациях менял порядок задач, чтобы тема, которая якобы «пришла в голову» ассистенту, возникала не сразу, а чуть позже. Для большего правдоподобия ассистенты могли бы иногда соглашаться друг с другом.
Также мне кажется неудачным камео Андрея Дмитриева (39:00). Понятно, зачем эта сценка нужна: прорекламировать следующий DotNext и следующий доклад. Но раз уж мы говорим, что кончилось время, хотя есть ещё задачки, то пусть всё выглядит, как будто это правда. Во-первых, выступать «под обрез» и не говорить, что у нас есть ещё несколько минут на вопросы. Во-вторых, засветить две-три дополнительных задачи с ответами и промотать слайды с ними в момент прерывания. Тогда народ, глядишь, заинтересуется, вдруг ещё эффект Зейгарник сработает, будут презентацию качать, всем хорошо.
А так у меня осталось недоумение: что это вообще было? Интеграл ещё…
Мне в некоторых местах не хватило понимания, что именно курили разработчики спецификации. Зачем-то же они сделали именно так? Это помогло бы не только лучше запомнить, но и отделить важные задачи от случайной ерунды. Посмотрим, например, на ранее упомянутое округление (начинается в 12:20):

Откуда взялось округление до ближайшего чётного? Почему оно включено по умолчанию? Когда нужен режим «прочь от нуля»? Возможно, только я всё пропустил, а нормальные люди давно знают, но я этот вопрос впервые в жизни осмыслил при подготовке данного разбора. Оказывается, режим носит название «банковское округление» и придуман в основном для случаев, когда нужно складывать деньги с центами/копейками в дробной части. Поскольку разных значений центов всего 100, хвост ровно в 50 центов будет встречаться в случайном наборе денежных сумм довольно часто. Если их все округлять прочь от нуля, мы накопим систематическую ошибку, а если к ближайшему чётному, то ошибки округления усреднятся примерно в ноль. При этом каждое конкретное число округляется детерминированно, а не в случайную сторону (а то есть и такой подход).
Поскольку считать деньги с помощью float и double не следует по многим причинам, настройки по умолчанию выглядят нелогичными. Но, по крайней мере, понятно, что за ними стоит. А если кто-то знает другой реалистичный сценарий использования банковского округления, поделитесь, пожалуйста.
Мне кажется, поднимать логику, стоящую за спецификацией, и рассказывать её зрителям — полезно и хорошо. Запоминать не только факты, но и их причины гораздо удобнее.
Вот кто сейчас вспомнит таблицу истинности для операций из упражнения 8 (начало 17:23), хотя в презентации она была?
Это вообще важно знать? Если бы понимать сценарии использования, которые имели в виду разработчики, восстановить её было бы легче.
Актуальность упражнения 10, напротив, не поставить под сомнение (начало на 21:18):
Андрей рассказывает, в каких ситуациях можно наступить на проблему с OverflowException и заканчивает рассказ оптимистичным пожеланием быть аккуратнее. А все ли сразу поняли, как именно нужно быть аккуратнее? Тут бы не помешали подробности.
Конечно, в ВУЗе у нас были фрагменты курсов, а то и целые курсы, посвящённые представлению данных. И конечно, про числа с плавающей точкой нам там рассказывали, но без практики многое забывается. В некоторых задачах Андрей затрагивает фундаментальные свойства типа float и double и вытекающие из них проблемы, но не вполне акцентирует на этом внимание зрителей. Самый яркий пример — задача про ассоциативность (упражнение 14, начало в 31:30):

Учитывая, что не все в зале ответили правильно, материал первого-второго курса стоит освежить. В данном случае важно, что числа распределены неравномерно: чем дальше от нуля, тем больше между ними промежутки. Давайте рассмотрим два соседних float'а максимального порядка (double по смыслу такие же, только рисовать больше):


С точки зрения рассматриваемого формата между ними ничего нет. При этом в реальном мире первое число равняется 1.7014122 * 1038, второе — 1.701412 * 1038, и разность между ними составляет 0.0000002 * 1038. Это, скажем аккуратно, офигительно много. Прибавить к числу максимального порядка единицу, тысячу или даже миллиард невозможно.
Зная эту механику, легко понять, как ещё нарушается правило ассоциативности: сумма нескольких маленьких чисел может оказаться больше, чем расстояние между двумя соседними большими, тогда как каждое маленькое число в отдельности будет просто уничтожено, если начинать сложение с большого числа.
В целом каждый паззлер — увлекательная история, которая даёт докладчику кредит внимания аудитории, и этим кредитом можно пользоваться, чтобы хотя бы из части загадок вывести какую-нибудь мораль (она там на самом деле есть!). Уверен, что доклад от этого выиграл бы.
Слайды сделаны хорошо, поэтому не стану придираться к мелочам, а отмечу решения, достойные подражания.
В докладе много слайдов с большим количеством информации. Сразу всё на экране разглядеть и понять трудно, но у Андрея все элементы возникают по очереди. Таким образом, зритель ни в какой момент не теряет того места, на которое нужно смотреть и о котором говорит докладчик. Это очень облегчает восприятие больших схем, кусков кода, списков. Делайте, как Андрей.
Пусть в презентации почти нет смешных картинок, если не считать Гомера Симпсона (которого, в принципе, можно было поискать в разрешении получше) и интеграла, она от этого не становится менее весёлой. Математика сама по себе — это весело.
При этом каждое упражнение оформлено одинаково, решение выделено одинаково, объяснение помечено в заголовке слайда — зритель быстро привыкает и ничто не отвлекает его от решения головоломок. Если у вас презентации много маленьких историй, имеет смысл придерживаться сходного оформления, как в данном случае.
Если вы хотите получить обратную связь по своему выступлению, то я с радостью вам её предоставлю.
Слайды можно найти здесь.
Дисклеймер: про реализацию арифметики только сам разбираемый доклад, а не собственно статья.
Сюжет
В этом месте нужно сказать, что я не очень люблю паззлеры. Они требуют знания покрытых мраком уголков спецификации, которое в реальной жизни обычно бесполезно. Просто представьте, что вы сопровождаете код, написанный любителем загадок.
Заметим, заставить человека самого подумать о чём-то важном, прежде чем рассказывать ему, «как правильно» — в общем случае хорошо, он гораздо лучше запомнит результат. Но начать с сути, то есть выбрать знание, которое нужно передать людям, и проиллюстрировать его парадоксальной задачей с простыми условиями — трудно. Для паззлеров часто проще взять те вещи, которые помнить не очень критично, зато их никто не знает, и сделать из них чистое развлечение.
В общем, внимательный читатель легко проследит в этой статье мою нелюбовь к жанру.
Сюжетные ходы и игра актёров
Нет ли тут противоречия: на сцену приходят помощники, чтобы создать иллюзию соревнования, но видно, что ответы и переходные реплики между задачами известны заранее. Например, на 12:00-12:20 Юля рассуждает о том, что приведение к целому — не та операция, и нужно использовать округление, и тут же появляется следующая задача, как раз на округление. Я бы в таких ситуациях менял порядок задач, чтобы тема, которая якобы «пришла в голову» ассистенту, возникала не сразу, а чуть позже. Для большего правдоподобия ассистенты могли бы иногда соглашаться друг с другом.
Также мне кажется неудачным камео Андрея Дмитриева (39:00). Понятно, зачем эта сценка нужна: прорекламировать следующий DotNext и следующий доклад. Но раз уж мы говорим, что кончилось время, хотя есть ещё задачки, то пусть всё выглядит, как будто это правда. Во-первых, выступать «под обрез» и не говорить, что у нас есть ещё несколько минут на вопросы. Во-вторых, засветить две-три дополнительных задачи с ответами и промотать слайды с ними в момент прерывания. Тогда народ, глядишь, заинтересуется, вдруг ещё эффект Зейгарник сработает, будут презентацию качать, всем хорошо.
А так у меня осталось недоумение: что это вообще было? Интеграл ещё…
Не только как, но и почему
Мне в некоторых местах не хватило понимания, что именно курили разработчики спецификации. Зачем-то же они сделали именно так? Это помогло бы не только лучше запомнить, но и отделить важные задачи от случайной ерунды. Посмотрим, например, на ранее упомянутое округление (начинается в 12:20):

Откуда взялось округление до ближайшего чётного? Почему оно включено по умолчанию? Когда нужен режим «прочь от нуля»? Возможно, только я всё пропустил, а нормальные люди давно знают, но я этот вопрос впервые в жизни осмыслил при подготовке данного разбора. Оказывается, режим носит название «банковское округление» и придуман в основном для случаев, когда нужно складывать деньги с центами/копейками в дробной части. Поскольку разных значений центов всего 100, хвост ровно в 50 центов будет встречаться в случайном наборе денежных сумм довольно часто. Если их все округлять прочь от нуля, мы накопим систематическую ошибку, а если к ближайшему чётному, то ошибки округления усреднятся примерно в ноль. При этом каждое конкретное число округляется детерминированно, а не в случайную сторону (а то есть и такой подход).
Поскольку считать деньги с помощью float и double не следует по многим причинам, настройки по умолчанию выглядят нелогичными. Но, по крайней мере, понятно, что за ними стоит. А если кто-то знает другой реалистичный сценарий использования банковского округления, поделитесь, пожалуйста.
Мне кажется, поднимать логику, стоящую за спецификацией, и рассказывать её зрителям — полезно и хорошо. Запоминать не только факты, но и их причины гораздо удобнее.
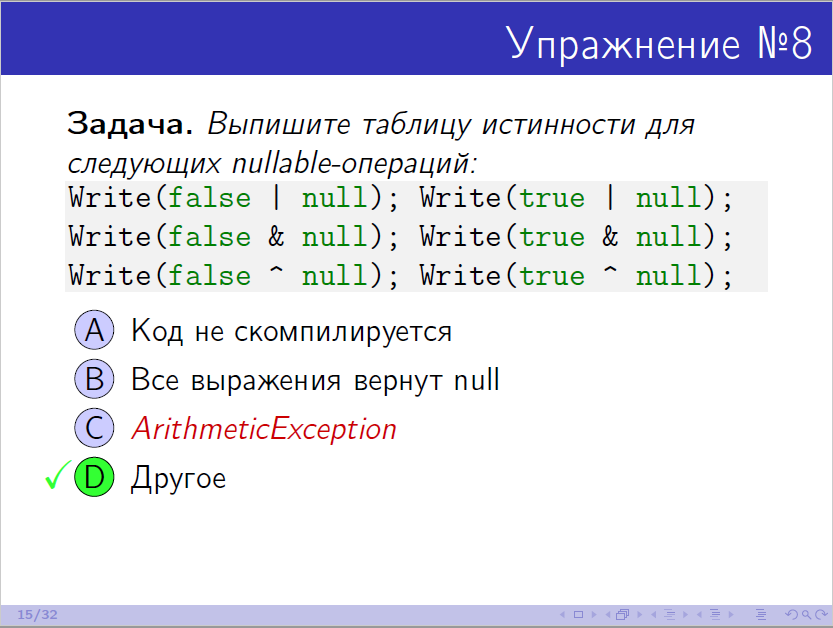
Вот кто сейчас вспомнит таблицу истинности для операций из упражнения 8 (начало 17:23), хотя в презентации она была?

Это вообще важно знать? Если бы понимать сценарии использования, которые имели в виду разработчики, восстановить её было бы легче.
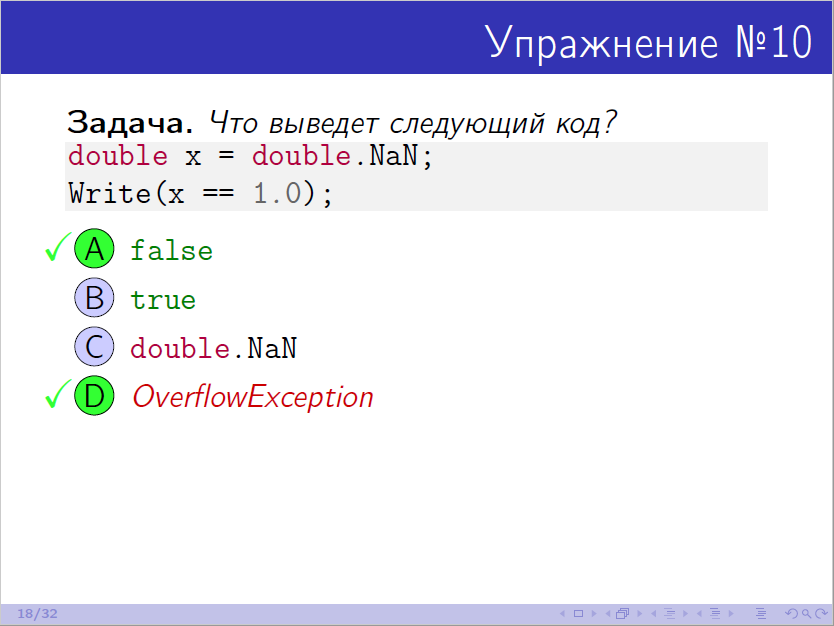
Актуальность упражнения 10, напротив, не поставить под сомнение (начало на 21:18):

Андрей рассказывает, в каких ситуациях можно наступить на проблему с OverflowException и заканчивает рассказ оптимистичным пожеланием быть аккуратнее. А все ли сразу поняли, как именно нужно быть аккуратнее? Тут бы не помешали подробности.
Как устроен float
Конечно, в ВУЗе у нас были фрагменты курсов, а то и целые курсы, посвящённые представлению данных. И конечно, про числа с плавающей точкой нам там рассказывали, но без практики многое забывается. В некоторых задачах Андрей затрагивает фундаментальные свойства типа float и double и вытекающие из них проблемы, но не вполне акцентирует на этом внимание зрителей. Самый яркий пример — задача про ассоциативность (упражнение 14, начало в 31:30):

Учитывая, что не все в зале ответили правильно, материал первого-второго курса стоит освежить. В данном случае важно, что числа распределены неравномерно: чем дальше от нуля, тем больше между ними промежутки. Давайте рассмотрим два соседних float'а максимального порядка (double по смыслу такие же, только рисовать больше):


С точки зрения рассматриваемого формата между ними ничего нет. При этом в реальном мире первое число равняется 1.7014122 * 1038, второе — 1.701412 * 1038, и разность между ними составляет 0.0000002 * 1038. Это, скажем аккуратно, офигительно много. Прибавить к числу максимального порядка единицу, тысячу или даже миллиард невозможно.
Зная эту механику, легко понять, как ещё нарушается правило ассоциативности: сумма нескольких маленьких чисел может оказаться больше, чем расстояние между двумя соседними большими, тогда как каждое маленькое число в отдельности будет просто уничтожено, если начинать сложение с большого числа.
Выводы
В целом каждый паззлер — увлекательная история, которая даёт докладчику кредит внимания аудитории, и этим кредитом можно пользоваться, чтобы хотя бы из части загадок вывести какую-нибудь мораль (она там на самом деле есть!). Уверен, что доклад от этого выиграл бы.
Слайды
Слайды сделаны хорошо, поэтому не стану придираться к мелочам, а отмечу решения, достойные подражания.
Последовательное появление элементов слайда
В докладе много слайдов с большим количеством информации. Сразу всё на экране разглядеть и понять трудно, но у Андрея все элементы возникают по очереди. Таким образом, зритель ни в какой момент не теряет того места, на которое нужно смотреть и о котором говорит докладчик. Это очень облегчает восприятие больших схем, кусков кода, списков. Делайте, как Андрей.
Единообразие
Пусть в презентации почти нет смешных картинок, если не считать Гомера Симпсона (которого, в принципе, можно было поискать в разрешении получше) и интеграла, она от этого не становится менее весёлой. Математика сама по себе — это весело.
При этом каждое упражнение оформлено одинаково, решение выделено одинаково, объяснение помечено в заголовке слайда — зритель быстро привыкает и ничто не отвлекает его от решения головоломок. Если у вас презентации много маленьких историй, имеет смысл придерживаться сходного оформления, как в данном случае.
Регулярные разборы
Если вы хотите получить обратную связь по своему выступлению, то я с радостью вам её предоставлю.
Что для этого нужно?
Всё это нужно отправить хабраюзеру p0b0rchy, то есть мне. Обещаю, что отзыв будет конструктивным и вежливым, а также осветит и положительные моменты, а не только то, что надо улучшать.
- Ссылка на видеозапись выступления.
- Ссылка на слайды.
- Заявка от автора. Без согласия самого докладчика ничего разбирать не будем.
Всё это нужно отправить хабраюзеру p0b0rchy, то есть мне. Обещаю, что отзыв будет конструктивным и вежливым, а также осветит и положительные моменты, а не только то, что надо улучшать.
Поделиться с друзьями
Комментарии (14)

pda0
02.02.2017 18:15Это довольно странно. Он говорит, что проверял на 64-битной системе. Но 64-битные приложения должны использовать SSE2, а не FPU. Разве CWR влияет на SSE2? Или .NET даже в 64-битном режиме продолжает FPU использовать?
P.S. А никто не подскажет, для 1С 8.3 какое значение CWR по умолчанию? ;-)
PsyHaSTe
02.02.2017 20:23Да, х64 использует SSE, только вот как это поможет решить проблему, связанную с самим типом данных?..

pda0
02.02.2017 21:58Я просто этот вопрос как-то не изучал, но разве команды sse2 подчиняются CWR и инициируют исключение? Я просто недавно немного возился с этим и заметил, что только в 32-битной программе у меня получается управлять режимом исключение/NaN, в 64 битах я всегда получел NaN на операциях с NaN…


ggrnd0
При суммировании округленных значений денег округление х.5 всегда вверх будет давать накопление ошибок.
В случае если округляется то вверх, то вниз накопление будет невилироваться.
Почему четное, а не нечетное не знаю.
p0b0rchy
Я скомпоновал текст неудачно: между вопросом и ответом большая картинка. Да, это действительно так, но понятно же, что для денег не надо использовать ни float, ни double с центами-копейками в дробной части, а других сценариев мне так сходу придумать не удалось.
ggrnd0
В этом то и дело.
Когда печатается чек, стоимость каждой позиции округляется до копеек, а потом суммируется в кассовом аппарате, где скорее всего есть только float.
В итоге, когда все проданные позиции проссумируются, вы можете из ниоткуда получить 100 рублей или потерять.
Diverclaim
Хм, но почему бы просто не считать все позиции и сумму в копейках, то есть складывать и вычитать integer? А уже при выводе обрабатывать 4450 как 44 р 50 коп.
ggrnd0
Потому что 2.37885768462 кг мяса, при стоимости 450 р/кг будут стоить 1070.48595808 р
Отсюда и округление...
Jef239
Купили 10 тонн рыбы по цене сто тысяч рублей за тонну. НДС 20% от суммы, то есть 1/6. Это будет 166 666 рублей 66 копеек. А вот теперь распределите эту рыбу по килограммам и граммам, чтобы сумма НДС сошлась. Удастся? :-) Так что минимум сотые копеекй нужны.
esaulenka
Нету в кассовом аппарате float'а. Более того, в кассовом аппрате рублей-то нет.
Чтобы не ходить по этим граблям, достаточно считать в копейках. В целых копейках.
ggrnd0
До целых копеек еще надо округлить...
Azoh
Есть еще decimal, для которого подобное округление нужно. Видимо для общности интерфейса решили сделать одинаковые методы.
p0b0rchy
Похоже, это самое правдоподобное объяснение. С учётом ветки комментариев выше, из всего этого на сцене нормальная такая дискуссия могла бы получиться.
Jef239
А что делать, если (реальная история 20летней давности) рыба продается килограммами, а цена — за тонну? И НДС считается с минимум с сотыми долями копейки. Так что fixed лучше, чем float, а вот расчет в целых копейках иногда не годится.