Есть две булевы функции аргументов, одна — константная, другая — сбалансированная. На какую сам сядешь, на какую фронтендера посадишь? Вот только функции неизвестны, а вызвать их разрешается лишь один раз.

Если не знаешь, как решить подобную задачу, добро пожаловать под кат. Там я расскажу про квантовые алгоритмы и покажу как их эмулировать на самом народном языке — на Python.

I’ve come to talk with you again

Давайте чуть более формально поставим задачу о двух функциях. Пусть дана булева функция и о ней априорно известно, что она или константна, то есть для любого из своих аргументов всегда возвращает либо 0, либо 1, или сбалансирована, то есть ровно на половине своих аргументов возвращает 0, а ровно на половине 1. Требуется определить, константна функция или сбалансирована. При этом считается, что время вызова функции несоизмеримо больше любых других операций, поэтому сложность алгоритма определяется количеством вызовов функции.


Пример:

1. сбалансирована:
   

   0	0	0
   0	1	1
   1	0	1
   1	1	0

   
   
2. константна:
   

   0	0	1
   0	1	1
   1	0	1
   1	1	1

   
   
3. ни сбалансирована, ни константна:
   

   0	0	0
   0	1	0
   1	0	0
   1	1	1

Задача, безусловно, искусственная и навряд ли когда-нибудь кому-нибудь встретится на практике, однако она — классический проводник в дивный новый мир квантовых вычислений, а нарушать традиции я не осмелюсь.

Классическое детерминированное решение

Давайте, для начала, решим задачу в классической модели вычислений. Для этого в худшем случае понадобится вызвать функцию на аргументах: ровно на половине и ещё одном. Если все вычисленные значения одинаковы, то функция, очевидно, константна. Если же существуют хотя-бы два различных результата, функция сбалансирована. Сложность детерминированного алгоритма экспоненциальна и составляет .

Алгоритм на Python:

from itertools import product, starmap, tee

def pairwise(xs):
    a, b = tee(xs)
    next(b, None)
    return zip(a, b)

def is_constant(f, n):
    m = 2 ** (n - 1)

    for i, (x, y) in enumerate(pairwise(starmap(f, product({0, 1}, repeat=n)))):
        if i > m:
            break

        if x != y:
            return False

    return True

Классическое вероятностное решение

А что, если вместо половины аргументов мы проверим меньшее их число и вынесем вердикт? Точным ответ уже не будет, но с какой вероятностью мы ошибёмся? Допустим, мы вычислили функцию на аргументах. Если среди значений функции есть два различных, то всё просто — функция сбалансирована. Иначе, мы объявляем её константной с вероятностью . Предположим, что мы ошиблись и функция на самом деле сбалансирована. Посчитаем вероятность ошибки . Если мы выбирали аргументы равномерно, то вероятность того, что два подряд идущих значения функции одинаковы, равна , а вероятность же встретить одинаковых подряд идущих значений равна . Таким образом:



Обратная функция:


При фиксированном сложность классического вероятностного алгоритма константна и равна Чтобы быть уверенным в ответе на 99.99%, необходимо вызвать функцию всего 14 раз.

Алгоритм на Python:

import random
from itertools import product, starmap, tee


def pairwise(xs):
    a, b = tee(xs)
    next(b, None)
    return zip(a, b)


def is_constant(f, n, k=14):
    xs = list(product({0, 1}, repeat=n))
    random.shuffle(xs)
    xs = xs[:k]

    for x, y in pairwise(starmap(f, xs)):
        if x != y:
            return False

    return True

А если я скажу вам, что существует константное детерминированное решение со сложностью , позволяющее вызвать функцию всего один раз?

Правда, прежде чем его рассмотреть, придётся отвлечься…

Because a vision softly creeping

Мифы

Пережде чем начать, хотелось бы обсудить несколько расхожих мифов, связанных с квантовыми вычислениями:

1. Квантовые алгоритмы — это сложно.
   
   
   
   
   Да, их сложно синтезировать, ибо требуется для этого математическое воображение и проницательность. Их сложно реализовывать на настоящих квантовых компьютерах: для этого необходимо превосходно знать физику и засиживаться каждый день допоздна в лаборатории на кафедре. Но что точно не требует никаких особых знаний и невероятного количества усердия, так это их понимание. Я утверждаю, что каждый может понимать квантовые алгоритмы: они опираются на крайне простую математику, доступную любому первокурснику. Всё, что от вас требуется — лишь немного времени на изучение.
   
   
2. Уже существуют квантовые компьютеры на тысячи кубитов от D-Wave
   Нет, это не настоящие квантовые компьютеры.
   
   
3. Не существует ни одного настоящего квантового компьютера
   Нет, существуют. В лабораторных условиях и располагают они лишь несколькими кубитами.
   
   
4. Квантовые компьютеры позволят решать задачи, недоступные ранее
   Нет, множество задач, вычислимых в классической и квантовой моделях, совпадают. Квантовые вычисления позволяют лишь снизить сложность небольшого подмножества этих задач.
   
   
5. На квантовом компьютере Crysis на максималках будет летать
   
   
   
   
   За исключением некоторого подмножества задач, которые квантовая модель вычислений способна ускорить, остальные могут быть решены лишь эмуляцией классического компьютера. Что, как вы понимаете, очень медленно. Crysis, скорее всего, будет лагать.
   
   
6. Квантовый компьютер — это чёрная коробочка с входом и выходом, заглянув в которую можно всё испортить
   
   
   
   
   Если вам 12 лет, такая аналогия сгодится. В любом другом случае она, как и все другие аналогии с коробками, котами, лупами и «связанными» нитками электронами, так активно продвигаемые во всех научно-популярных источниках, только лишь запутывает, создаёт иллюзию ложного понимания и скорее вредна, чем полезна. Откажитесь от этих аналогий.
   

Зачем?

Зачем прикладному математику (программисту) уметь разбираться в квантовых алгоритмах на прикладном уровне? Тут всё просто, я готов предложить вам два довода:

1. Для саморазвития. Почему бы и нет?
   
2. Они уже идут. Они, квантовые компьютеры. Они уже рядом. Моргнуть не успеете, как парочка появится в серверной вашей компании, а ещё через несколько лет и в виде сопроцессора в вашем ноутбуке. И бежать уже будет некуда. Придётся под них программировать, вызывать квантовые сопрограммы. А без понимания это делать сложно, согласитесь.
   

Left its seeds while I was sleeping

Самой базовой составляющей квантовых вычислений является квантовая система. Квантовая система — физическая система, все действия которой сравнимы по величине с постоянной Планка. Это определение и тот факт, что квантовые системы подчиняются законам матричной механики — все знания, которые нам потребуются из физики. Дальше — только математика.


Как и любая другая физическая система, квантовая система может находиться в определённом состоянии. Все возможные состояния квантовой системы образуют гильбертово пространство над полем комплексных чисел. Надеюсь, с концепцией комплексных чисел читатель знаком — их понимание необходимо везде в дальнейшем. Если нет, советую познакомиться и возвращаться. Гильбертово пространство же является полным нормированным метрическим линейным пространством с нормой , где — скалярное произведение. По порядку с конца:

1. Линейное (векторное) пространство — множество элементов с введёнными на нём операциями сложения элементов и умножения на элемент поля (в нашем случае поля комплексных чисел). Операции эти должны быть замкнуты (результат должен принадлежать множеству ) и должны выполняться 8 аксиом. Посмотреть полный их список, а так же познакомиться подробнее с линейными пространствами рекомендую здесь.
   
   
2. В метрическом пространстве для любых элементов определено расстояние , которое удовлетворяет требованиям (аксиомам метрического
   пространства):
   
   
   • , при этом тогда и только тогда, когда и совпадают;
     
   • ;
     
   • — неравенство треугольника.
     
   
   
3. В нормированном пространстве для любого элемента существует вещественное число , называемое его нормой и удовлетворяюещее, опять же, трём аксиомам:
   
   
   • , если же , то — нулевой элемент;
     
   • ;
     
   • .
     
   
   

Введём в полученном пространстве скалярное произведение, удовлетворяющее обычным требованиям скалярного произведения, введём норму как показано выше и получим пространство Гильберта.


Обсудим ещё понятие сопряжённого пространства. Пространством, сопряжённым к называется пространство линейных операторов над . Что такое линейный оператор? Можно думать о нём как об обобщении линейной функции: для линейноного оператора должно выполняться:


где , . (На самом деле, ещё и его норма должна быть ограничена на единичной гиперсфере, но, дабы избежать ещё десятка громоздких определений, ограничимся таким интуитивным представлением.)

В квантовой информатике по историческим причинам используются обозначения Дирака. Они могут казаться необоснованно громоздкими и вычурными, но они — стандарт, которого стоит придерживаться. В этих обозначениях элемент нашего гильбертова пространства, описывающий состояние системы, называется кет-вектором и обозначается


Бра-вектором называется элемент сопряжённого пространства


такой что


То есть, это линейный оператор, применение которого к нашему вектору состояния аналогично скалярному произведению на соответствующий ему элемент «оригинального» гильбертова пространства. Для удобства записи при приминении бра-вектора к кет-вектору две вертикальные черты сливаются в одну, что показано в выражении выше.

Важно то, что вектора, отличающиеся лишь умножением на некоторую ненулевую константу, отвечают одному и тому же физическому состоянию, поэтому часто рассматривают не все возможные состояния, а лишь нормированные, то есть такое подмножество , что


— норма каждого элемента равна единице. Все такие вектора живут на единичной гиперсфере.

Если мы выделим в нашем гильбертовом пространстве состояний некоторый базис , то любой кет-вектор сможем записать в виде вектора комплексных чисел — коэффициентов его разложения по этому базису:


при этом матричная механика говорит нам, что квадраты модулей коэффициентов разложения физически означают вероятности нахождения квантовой системы в соответствующем базисном состоянии при измерении в этом базисе.

Вот оно — первое и основное свойство квантовых систем, которое так часто мусолят в популярных статьях: если измерить систему в некотором базисе, то она перейдёт в одно из базисных состояний, потеряет информацию и не сможет вернуться назад. Вот только при прочтении складывается ощущение, что всё происходит абсолютно случайно и повлиять на это никак нельзя, тогда как на самом деле вероятности перехода известны заранее и, более того, зависят от измерительного базиса. Если бы всё было так случайно, как нам представляют, детерминированные квантовые алгоритмы были бы невозможны.

Если мы можем представить элемент Гильбертова пространства вектором при некотором фиксированном базисе, то линейный оператор над этим пространством мы можем представить матрицей.

Действительно,


эквивалентно


где получается поочерёдным применением оператора к базисным элементам и выписыванием получившихся элементов по строкам, а — разложение в этом же базисе.

Пусть оператор представляется матрицей


Элементы матрицы — комплексные числа. Давайте возьмём каждый элемент и заменим его комплексно сопряжённым (комплексно сопряжённым к называется число ) и, заодно, транспонируем всю матрицу:


Такая матрица называется эрмитово-сопряжённой к . Если , где — единичный оператор (с единичной матрицей), то соответствующий оператор называется унитарным.

Второе правило, которое диктует нам матричная механика: на квантовую систему могут действовать только унитарные операторы. Почему? Потому что такие преобразования обратимы во времени и не теряют информацию. Действительно, если


то можно применить обратное преобразование


и получить исходное состояние системы.

Напоследок самое важное: тензорное произведение. Тензорным произведением двух гильбертовых пространств и называется гильбертово пространство, обозначаемое . Я не буду приводить формальное определение, лишь отмечу важные нам свойства:

1. Размерность получившегося пространства равна произведению размерностей исходных пространств:
   ;
   
2. Если — базис , а — базис , то — порождающий базис .
   

Тензорным же произведенем операторов из и из (оператор представлен матрицей, показанной выше) называется оператор из с матрицей


Такое произведение ещё называется произведением Кронекера: мы умножаем вторую матрицу на каждый элемент первой матрицы и из получившихся блоков составляем блочную матрицу. Если размерность A равнялась , а размерность B равнялась , то размерность матрицы, полученной в ходе тензорного произведения, будет равна .

Пример:






Третье важное свойство квантовых систем: две квантовые системы могут находиться в состоянии суперпозиции, при этом новое пространство состояний представляет собой тензорное произведение исходных пространств, а состояние новой системы будет являться тензорным произведением состояний исходных систем. Так, суперпозицией систем в состояниях и будет новая система в состоянии , описываемая гильбертовым пространством .

And the vision that was planted in my brain

Вот и вся математика, что нам понадобится. На всякий случай, резюмируя:

1. При фиксированном базисе квантовую систему можно описать комплексным вектором, а эволюцию этой системы — унитарной комплексной матрицей;
   
2. Квантовую систему можно измерить в каком-либо базисе и она перейдёт в одно из базисных состояний в соответствии с заранее определёнными вероятностями.
   

Получается, чтобы описывать, изучать, понимать и эмулировать на классическом компьютере квантовые алгоритмы, достаточно лишь умножать матрицы на вектора — это даже проще, чем нейронные сети: здесь нет нелинейностей!

Кубит

Давайте рассмотрим некоторую квантовую систему, описываемую двумерным гильбертовым пространством и выделим в ней некоторый базис, вектора которого обозначим как и . Внутри скобок записывается индекс базисного вектора в двоичной системе счисления, начиная с нуля без дополнительных символов. Такие обозначения окажутся очень удобными. Таким образом,


и произвольный вектор можно выразить следующим образом:


где и — некоторые комплексные числа, такие что (вспомните интерпретацию коэффициентов разложения и условие нормировки из предыдущего параграфа). Так вот, такая простая квантовая система называется кубитом (quantum bit, qbit). Кубит — аналог классического бита в квантовой модели вычислений. Нетрудно видеть, что пространство всевозможных состояний одного кубита представляет из себя трёхмерную сферу, называемую сферой Блоха, где соответствует нижнему полюсу, а — верхнему.

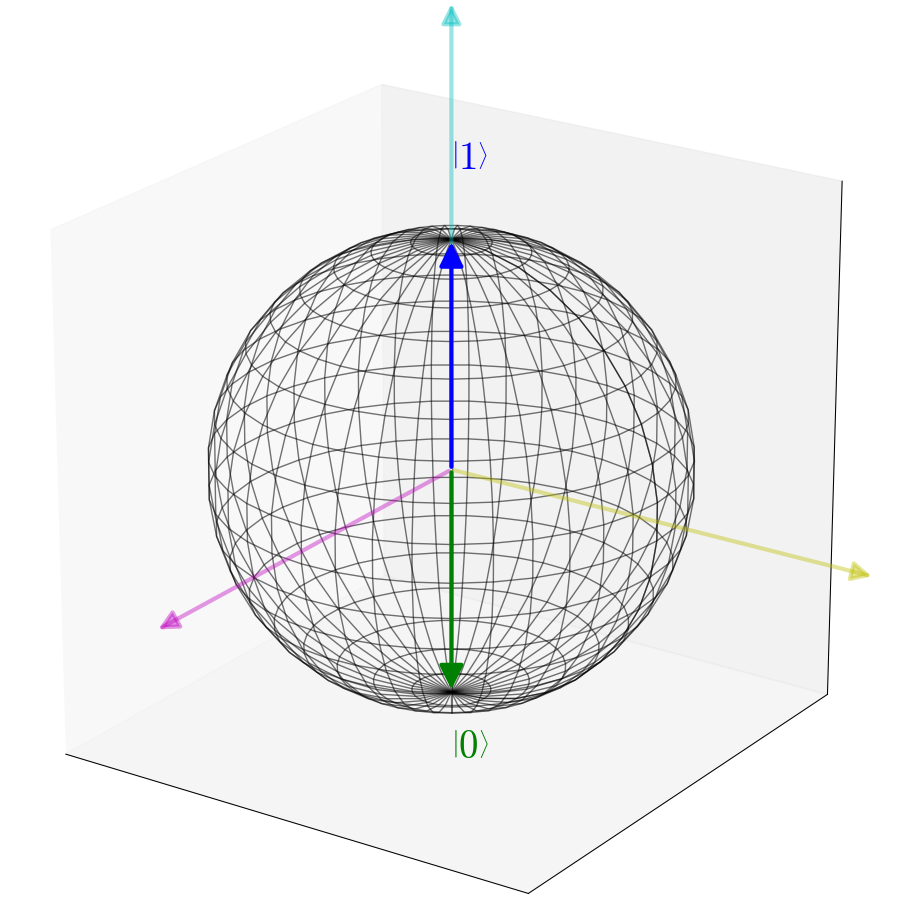
Регистр

Один кубит, как и один бит — слишком скучно, поэтому сразу рассмотрим суперпозицию нескольких кубитов. Такая суперпозиция называется квантовым регистром (quantum register, qregister) из кубитов. Например, квантовый регистр из 2 кубитов будет описываться пространством и иметь 4 базисных состояния:





Соответственно, любое состояние такого регистра можно представить в виде


где . Заметьте, что в наших обозначениях базисный вектор с единицей на -ом месте обозначется числом , записанным в двоичном виде.

Далее аналогично. Квантовый регистр из кубитов будет описываться -мерным гильбертовым пространством , иметь базисных состояний, формируемых аналогичным образом. Не откладывая надолго, научимся эмулировать квантовые регистры:

import numpy as np


class QRegister:
    def __init__(self, n_qbits, init):
        self._n = n_qbits
        assert len(init) == self._n

        self._data = np.zeros((2 ** self._n), dtype=np.complex64)
        self._data[int('0b' + init, 2)] = 1

3 строчки кода для создания квантового регистра — совсем не сложно, согласитесь. Использовать можно таким образом:

a = QRegister(1, '0')    # |0>
b = QRegister(1, '1')    # |1>
c = QRegister(3, '010')  # |010>

Квантовый алгоритм включает в себя:

1. Инициализацию квантового регистра;
   
2. Набор унитарных преобразований над ним;
   
3. Измерение результата.
   

Измерение

С первым пунктом разобрались и научились его эмулировать, давайте теперь научимся эмулировать последний: измерение. Как вы помните, квадраты коэффициентов вектора состояния физически означают вероятности перехода в это состояние. В соответствии с этим реализуем новый метод в классе QRegister:

def measure(self):
    probs = np.real(self._data) ** 2 + np.imag(self._data) ** 2
    states = np.arange(2 ** self._n)
    mstate = np.random.choice(states, size=1, p=probs)[0]
    return f'{mstate:>0{self._n}b}'

Генерируем вероятности probs выбора одного из состояний states и случайно выбираем его с помощью np.random.choice. Остаётся только вернуть бинарную строку с соответствующим количеством дополняющих нулей. Очевидно, что для базисных состояний ответ всегда будет одинаков и равен самому этому состоянию. Проверим:

>>> QRegister(1, '0').measure()
'0'
>>> QRegister(2, '10').measure()
'10'
>>> QRegister(8, '01001101').measure()
'01001101'

Почти всё готово, чтобы решить нашу задачу! Осталось лишь научиться влиять на квантовые регистры. Мы уже знаем, что сделать это можно унитарными преобразованиями. В квантовой информатике унитарное преобразование называется гейтом (quantum gate, qgate, gate).

Гейты

В рамках данной статьи рассмотрим лишь малое число самых основных гейтов, которые нам пригодятся. На самом деле, их намного больше.

Единичный

Единичный гейт — самый простой, какой только можно рассмотреть. Его матрица выглядит следующим образом:


Он никак не изменяет кубит, на который действует:


однако не стоит считать его бесполезным — он нам понадобится, и не раз.

Гейт Адамара

Не составляет труда проверить, что матрица унитарна:


Рассмотрим действие гейта Адамара на базисные кубиты:



Или в общем виде [1]:


Как можно заметить, гейт Адамара любое базисное состояние переводит в равновероятное — при измерении с равной вероятностью можно получить любой результат.

Гейты Паули

Три крайне важных гейта, которым соответствуют матрицы, введённые Вольфгангом Паули:


Гейт ещё называется NOT-гейтом:


а геометрически его применение эквивалентно повороту на сфере Блоха на радиан вокруг оси .


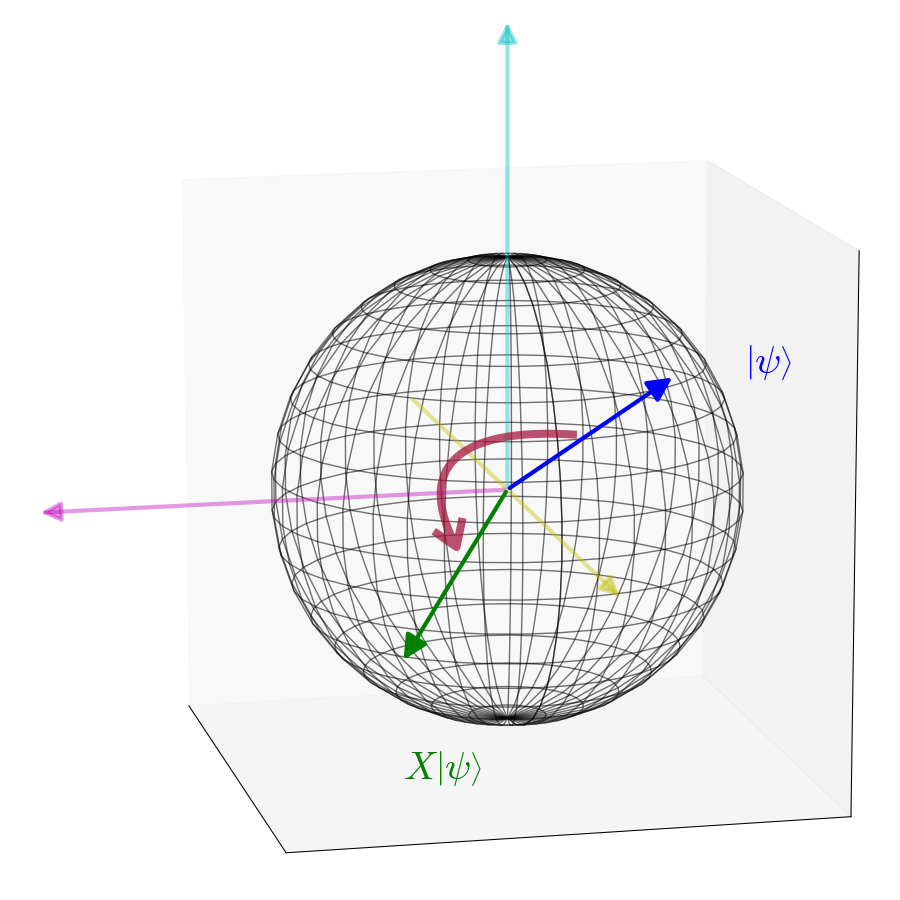
Гейты и аналогичны гейту за тем исключением, что вращение производится вокруг соответствующей оси.

Существует теорема, согласно которой с помощью гейтов , , и можно выразить любой однокубитный гейт. Например:


откуда видно, что гейт Адамара геометрически означает вращение на радиан вокруг оси .

Реализуем все рассмотренные гейты на Python. Для этого создадим ещё один класс:

class QGate:
    def __init__(self, matrix):
        self._data = np.array(matrix, dtype=np.complex64)

        assert len(self._data.shape) == 2
        assert self._data.shape[0] == self._data.shape[1]

        self._n = np.log2(self._data.shape[0])

        assert self._n.is_integer()

        self._n = int(self._n)

А в класс QRegister добавим операцию применения гейта:

def apply(self, gate):
    assert isinstance(gate, QGate)
    assert self._n == gate._n
    self._data = gate._data @ self._data

И создадим уже известные нам гейты:

I = QGate([[1, 0], [0, 1]])
H = QGate(np.array([[1, 1], [1, -1]]) / np.sqrt(2))
X = QGate([[0, 1], [1, 0]])
Y = QGate([[0, -1j], [1j, 0]])
Z = QGate([[1, 0], [0, -1]])

Орёл или решка?

Давайте для примера рассмотрим простейший квантовый алгоритм: он будет генерировать случайный бит — ноль или один, орла или решку. Это будет самая честная монета во вселенной — результат станет известен лишь при измерении, а природа случайности зашита в само основание вселенной и повлиять на неё невозможно никоим образом.

Для алгоримта нам понадобится всего один кубит. Пусть в начальный момент времени он находится в состоянии :


Теперь применим к нему гейт Адамара чтобы получить состояние


Если мы сейчас измерим полученную систему, с вероятностью она окажется в состоянии и с точно такой же вероятностью в состоянии . Останется только записать полученный результат.

Проверим алгоритм, эмулируя его на нашем классическом компьютере:

from quantum import QRegister, H


def quantum_randbit():
    a = QRegister(1, '0')
    a.apply(H)

    return a.measure()


for i in range(32):
    print(quantum_randbit(), end='')
print()

Результаты:

? python example-randbit.py
11110011101010111010011100000111

? python example-randbit.py
01110000111100011000101010100011

? python example-randbit.py
11111110011000001101010000100000

Весь приведённый выше алгоритм может быть записан парой формул:


Однако, с такой записью не очень удобно работать: структура списка — последовательности действий, хорошо подходящая для классических алгоритмов, не применима в квантовом случае: здесь у нас нет ни циклов, ни условий, лишь течение состояния вперёд (а иногда и назад) во времени. Поэтому для описания алгоритмов в квантовой информатике широко используются квантовые схемы. Вот схема приведённого выше алгоритма:

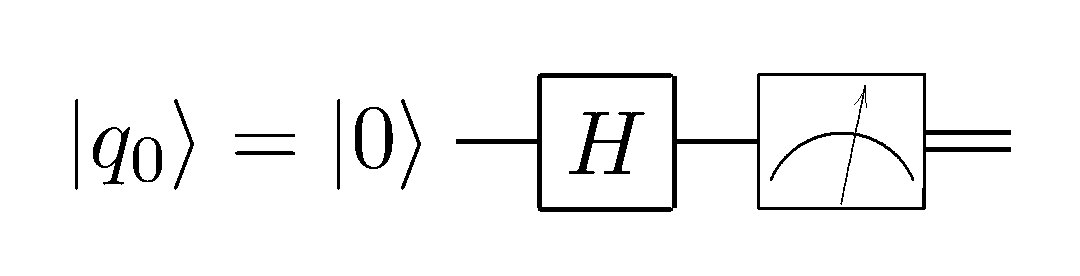
Слева всегда обозначено исходное состояние системы. В прямоугольниках указываются унитарные преобразования, производимые над этим состоянием, а в конце на всех или на нескольких кубитах распологается значок измерительного прибора — операция измерения. Существует ещё «синтаксический сахар» для некоторых многокубитных преобразований в виде точек, разветвлений и кружочков. И всё. Если вы умеете отличать квадрат от треугольника и круга, вы без проблем поймёте любую схему квантового алгоритма.

Больше кубитов богу кубитов

А что, если мы работаем не с одним кубитом, а с целым их регистром? И, допустим, хотим применить гейт лишь к одному кубиту? На помощь приходят свойства тензорного произведения. По определению тензорного произведения оператора и :


где , . Тогда:


то есть, всё равно — применить ли гейт к одному кубиту, а затем связать его со вторым и получить квантовый регистр или же применить ко всему регистру оператор . Аналогично, если мы хотим применить оператор только ко второму кубиту, мы можем применить ко всему регистру оператор . Это значит, что такая схема:


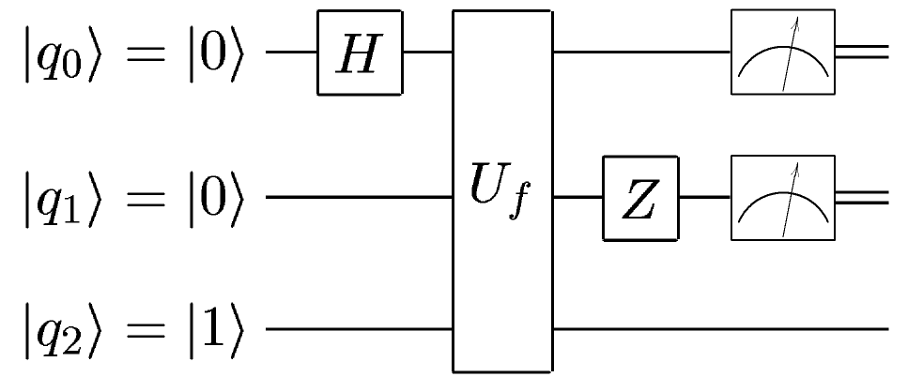
Полностью аналогична такой:


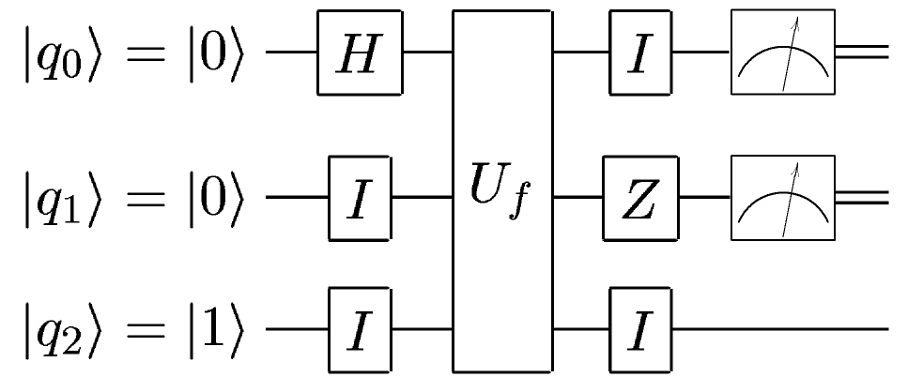
Только единичные гейты для удобства опускают.

А если мы, наоборот, хотим применить гейт сразу к нескольким кубитам? Опять же, из определения тензорного произведения, для этого мы можем применить к ним этот гейт, тензорно умноженный сам на себя необходимое количество раз:


означает тензорное возведение в степень. Кстати, для краткости записывают как . Таким образом,


означает: к каждому кубиту квантового регистра из нулевых кубитов применить преобразование Адамара.

Добавим тензорное произведение и возведение в степень в наш QGate:

def __matmul__(self, other):
    return QGate(np.kron(self._data, other._data))

def __pow__(self, n, modulo=None):
    x = self._data.copy()

    for _ in range(n - 1):
        x = np.kron(x, self._data)

    return QGate(x)

Квантовый оракул

Каждой бинарной функции соответствует единственный многокубитный гейт размерности , который обозначается и называется квантовым оракулом для этой функции. Он содержит в себе всю информацию о функции и «позволяет» одновременно вызвать её на всех её возможных аргументах.

Почему его размерность ? Всё дело в том, что согласно ещё одному фундаментальному свойству квантовых вычислений, в них не теряется информация и они обратимы во времени. Если мы в классической модели вычислений вызовем функцию и получим результат, то по нему одному мы не сможем сказать, с какими аргументами функция была вызвана и, соответственно, не сможем обратить вычисления во времени.



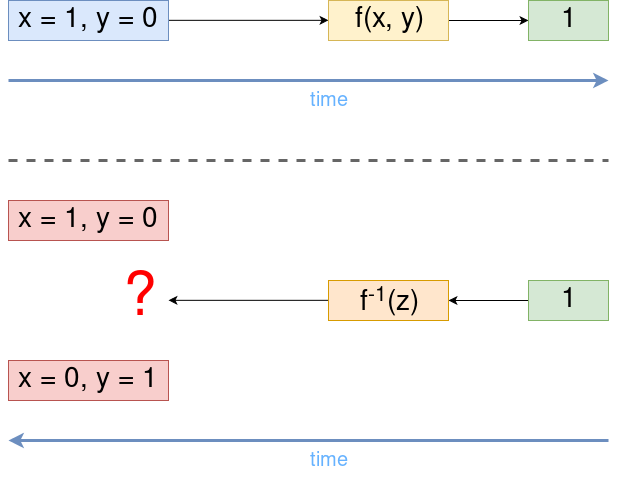
Один из способов избежать этого — запомнить аргументы, с которыми была вызвана функция.



То же самое происходит и в квантовой модели вычислений, только там оно встроено в саму их природу — без сохранения полной информации невозможно построить унитарное преобразование.

Квантовый оракул определяется как унитарное преобразование, переводящее состояние в состояние , где кубитов, обозначенных , несут в себе информацию об аргументе функции и остаются неизменными, а единственный кубит — её результат. обозначает сложение по модулю 2.

Разберёмся на примере. Допустим, мы хотим построить оракул для функции одного аргумента . Значит, соответствующий оператор будет двухкубитным и может быть описан квадратной матрицей размерности . В соответствии с описанным выше правилом посмотрим, в какие состояния должны перейти все возможные базисные состояния регистра:





Оператор с единичной матрицей переводит любое состояние в себя же, так как при умножении матрицы на -ую строку мы берём -ый же компонент вектора и ставим его на то же самое место. Если в матрице на -ой строке все элементы кроме -го будут нулями, а он единицей, то на -ое место результирующего вектора мы поставим элемент, который стоял на -ом месте исходного вектора. В примере выше нам нужно оставить на месте и элементы вектора состояния и поменять местами и элементы. Тогда будет выглядеть следующим образом:


Проверим:


Аналогично для любой другой функции произвольного числа аргументов. Реализуем оракл:

def U(f, n):
    m = n + 1

    U = np.zeros((2**m, 2**m), dtype=np.complex64)

    def bin2int(xs):
        r = 0
        for i, x in enumerate(reversed(xs)):
            r += x * 2 ** i
        return r

    for xs in product({0, 1}, repeat=m):
        x = xs[:~0]
        y = xs[~0]

        z = y ^ f(*x)

        instate = bin2int(xs)
        outstate = bin2int(list(x) + [z])
        U[instate, outstate] = 1

    return QGate(U)

Still remains

Ну вот мы и рассмотрели весь базис, который необходим для решения поставленной задачи и даже успели написать небольшой фреймворк на питоне, который нам поможет это решение проверить. Алгоритм, позволяющий за один вызов функции определить, константна функция или сбалансирована, именуется алгоритмом Дойча — Йожи. Версия алгоритма для функции одной переменной была разработанна в 1985 году Дэвидом Дойчем, а затем обобщёна на случай нескольких переменных в 1992 году с помощью Ричарда Йожи. Вот схема этого алгоритма:


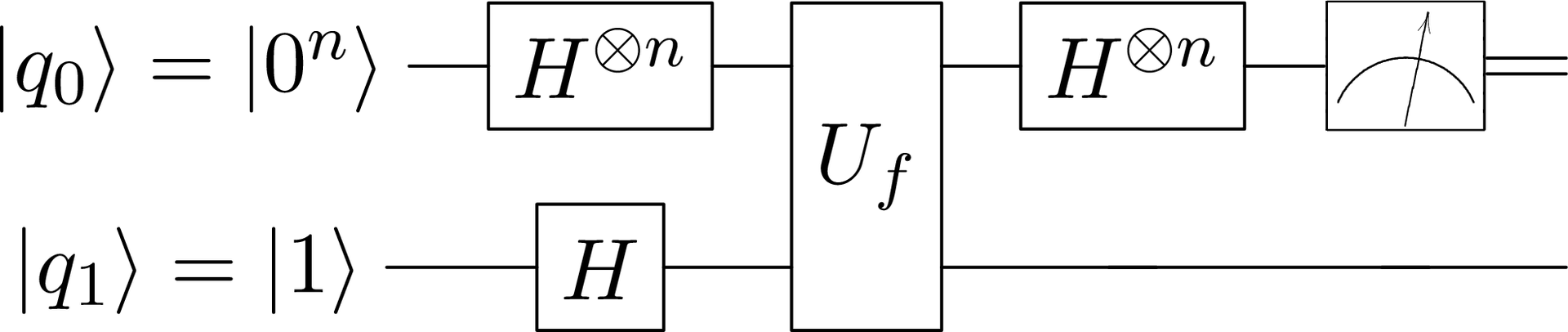
Если результатом измерения станет 0, то функция константна, иначе — сбалансирована. Сразу реализуем алгоритм:

from quantum import QRegister, H, I, U


def is_constant(f, n):
    q = QRegister(n + 1, '0' * n + '1')
    q.apply(H ** (n + 1))
    q.apply(U(f, n))
    q.apply(H ** n @ I)

    if q.measure()[:~0] == '0' * n:
        return True
    else:
        return False

И проверим:

def f1(x):
    return x


def f2(x):
    return 1


def f3(x, y):
    return x ^ y


def f4(x, y, z):
    return 0


print('f(x) = x is {}'.format('constant' if is_constant(f1, 1) else 'balansed'))
print('f(x) = 1 is {}'.format('constant' if is_constant(f2, 1) else 'balansed'))
print('f(x, y) = x ^ y is {}'.format('constant' if is_constant(f3, 2) else 'balansed'))
print('f(x, y, z) = 0 is {}'.format('constant' if is_constant(f4, 3) else 'balansed'))

Результат:

f(x) = x is balansed
f(x) = 1 is constant
f(x, y) = x ^ y is balansed
f(x, y, z) = 0 is constant

Работает. Замечательно. А почему он работает? Докажем корректность алгоритма и заодно посмотрим на принцип его работы.

Рассмотрим действие гейта на квантовый регистр в произвольном базисном состоянии [1]:


(по свойству тензорного произведения)


(применим к каждому отдельному кубиту)


(вынесем -1 за знак тензорного произведения)


(переобозначим для компактности)


где — сложение по модулю 2, а — скалярное произведение по модулю 2.

В начальный момент времени система находится в состоянии и под действием преобразования Адамара перейдёт в состояние


Оракул переведёт систему в состояние


Заметьте, что если на некотором фиксированном аргументе функция примет значение 0, то коэффициент перед не изменится, иначе — поменяет знак. Исходя из этого наблюдения можно переписать текущее состояние как


На данном этапе отбросим неиспользуемый далее последний кубит и применим повторное преобразование Адамара к первым кубитам, чтобы получить состояние


А так как , вероятность наблюдения исхода равна


Вот и всё. Мы рассмотрели достаточно упрощённую модель квантовых вычислений, написали мини-фреймворк на питоне для их эмуляции на классическом компьютере и разобрали один из самых простых «настоящих» квантовых алгоритмов — алгоритм Дойча-Йожи. Вот котик для тех, кто не поленился, прочитал статью и разобрался в теме:


> С кодом можно ознакомиться на GitHub

Спасибо за прочтение! Ставьте лайки, подписывайтесь на профиль, оставляйте комментарии, занимайтесь полезными делами. Дополнения приветствуются.

Литература

• [1] М. Вялый, «Квантовые алгоритмы: возможности и
  ограничения»
  
• [2] А. С. Холево, «Введение в квантовую теорию информации»
  
• [3] M. A. Nielsen, «Quantum Information Theory»
  

P.S: Формулы на хабре — отстой. Спасибо Roman Parpalak за сервис upmath.me, без него пост с таким количеством формул был бы невозможен.