Learning to learn

В этот раз я проводил эксперименты на тему learning to learn, то есть алгоритмов, которые могут учиться, как лучше учиться.

Цели эксперимента:

1) Создать алгоритм оптимизации, который можно некоторым стандартным способом приспособить к любой оптимизационной задаче или множеству задач. Под словом «приспособить» я имею в виду «сделать, чтобы алгоритм очень хорошо справлялся с этой задачей».
2) Подстроить алгоритм под одну задачу и посмотреть, как изменилась его эффективность на других задачах.

Почему алгоритмы оптимизации вообще важны?

Потому что очень многие задачи можно свести к задачам оптимизации. Например, в этой статье вы можете увидеть, как свести задачу управления транспортным средством к задаче оптимизации.
В примере мы будем тестировать алгоритм на более традиционных задачах оптимизации, так как этот тест займёт меньше времени, чем обучение нейросети.

Список задач

Задачи у нашего алгоритма будут следующие:

1) Задача на полиномиальную регрессию. Дана некоторая функция, надо построить кривую, которая будет аппроксимировать график этой функции графиком многочлена 7-ой степени. Оптимизатор подбирает коэффициенты регрессии. Метрика качества в этой задаче равна среднему отклонению между реальным графиком и аппроксимацией. У функции много локальных оптимумов, но она гладкая.
2) Задача на квадратичную функцию. Метрика качества q=(k1-10)^2+(k2+15)^2+(k3+10*k4-0.06)^2+…, то есть она равна сумме квадратов от неких линейных функций от коэффициентов, которые подбирает оптимизатор. У функции много минимумов, но она гладкая.
3) Задача на дискретную функцию. Метрика качества рассчитывается по алгоритму вида: q=1; если(k1>-2){q+=3}; если(k1<0.2){q+=15};…, то есть график функции от любой переменной будет выглядеть как некоторая ступенчатая линия. У функции мало локальных оптимумов, но она негладкая.

В качестве тренировочной задачи я буду применять задачу 2 (на квадратичную функцию), в качестве тестовых – остальные две.

Оптимизатор

В качестве оптимизирующего алгоритма я буду использовать свой самописный ансамбль алгоритмов, который я назвал Абатуром. Данный ансамбль включает в себя несколько вариантов покоординатного спуска, градиентный спуск, эволюцию, алгоритм пчелиного роя. И управляющий алгоритм, который с разной вероятностью вызывает разные модули.

Так выглядит основной блок принятия решений в Абатуре.

for i=1:sz(2)
%optimizerData.optimizers - массив оптимизирующих алгоритмов
            reputation(i)=optimizerData.optimizers{i}.reputation;
%optimizerData.optimizers{i}.reputation - один из параметров Абатура, он настраивается в ходе обучения
            reputationR(i)=reputation(i)*(1+0.5*randD());
end;
[ampl,arg]=max(reputationR);
[newK,dt]=feval(optimizerData.optimizers{arg}.name,optimizerData);
optimizerData.dt=optimizerData.dt+dt;
valNew=feval(optimizerData.func,newK);
if(valNew>=valOld)
            optimizerData.kArr=newK;
            valOld=valNew;
end;

optimizerData.k — это массив параметров Абатура. Как видно в коде выше, эти параметры определяют всё: шаги градиентного спуска, размеры популяций, вероятности срабатывания того или иного оптимизатора.

Сам Абатур не может изменить эти параметры, но их может изменить какой-нибудь другой алгоритм, который занимается оптимизацией Абатура. Обучение Абатура состоит в подборе параметров k, которые максимизируют его метрику.

Метрика качества learning to learn

Для оптимизации способности к оптимизации надо каким-то способом измерять эту самую способность к оптимизации. Я применял метрику lrvt (logarithm-relative-value-time).
Lrvt=((log(abs(valOld/valNew))/log(10)))/log(dt+10)
ValOld – метрика качества до оптимизации
ValNew – метрика качества после оптимизации
Dt – количество вычислений оптимизируемой функции в ходе оптимизации.

Эту метрику я не придумал единоразово, это результат длительной эволюции моих метрик качества. Эта метрика коррелирует с valOld/valNew, то есть с количественным значением апгрейда и антикоррелирует с dt, то есть затратами времени на апгрейд.

Испытание 1. Градиентный спуск.

Запустим алгоритм градиентного спуска на всех трёх перечисленных задачах – просто, чтобы было, с чем сравнивать Абатур. По горизонтальной оси откладывается номер шага, по вертикальной – метрика качества (идеальное решение найдено, если она равна 0).

1) Регрессия.



Градиентный спуск снизил q с 1.002 до 0.988 за 100 тактов. Слабовато, но стабильно.

2) Квадратичная функция



Градиентный спуск снизил q со 140 до примерно 5 за 100 тактов. Сильно, но алгоритм уже вышел в насыщение.

3) Дискретная функция



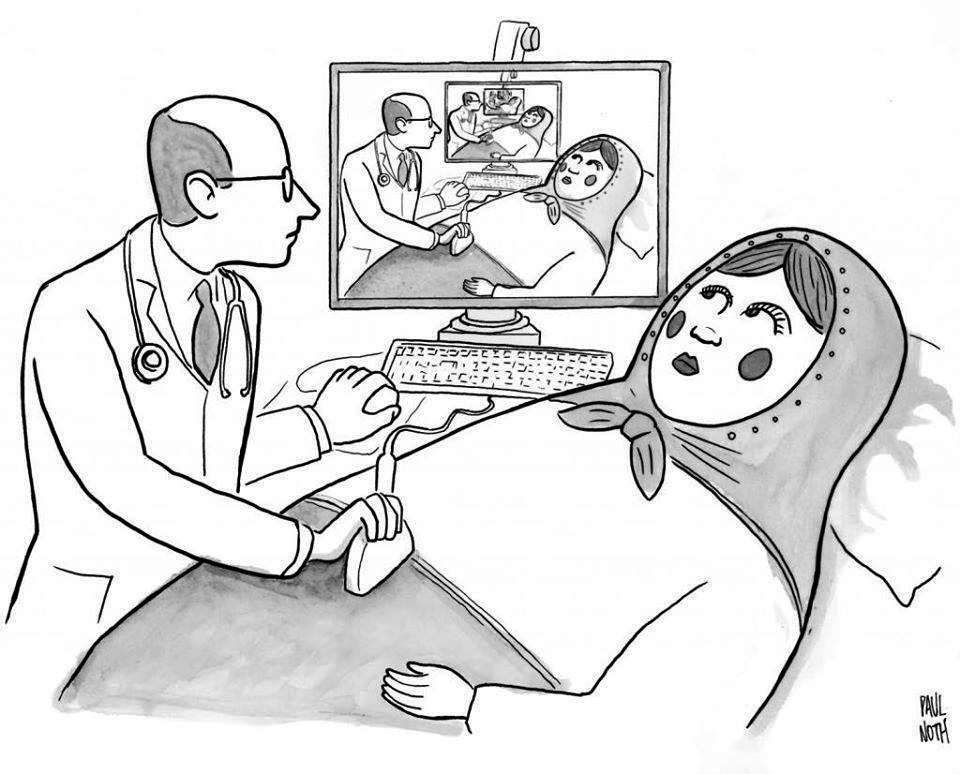
Градиентный спуск снизил q со 3663.06 до 3662.98 за 100 тактов. Очень слабо, очень непостоянно.

Испытание 2. Абатур с настройками по умолчанию.

Теперь запустим на этих же задачах Абатур со стандартными настройками.

1) Регрессия



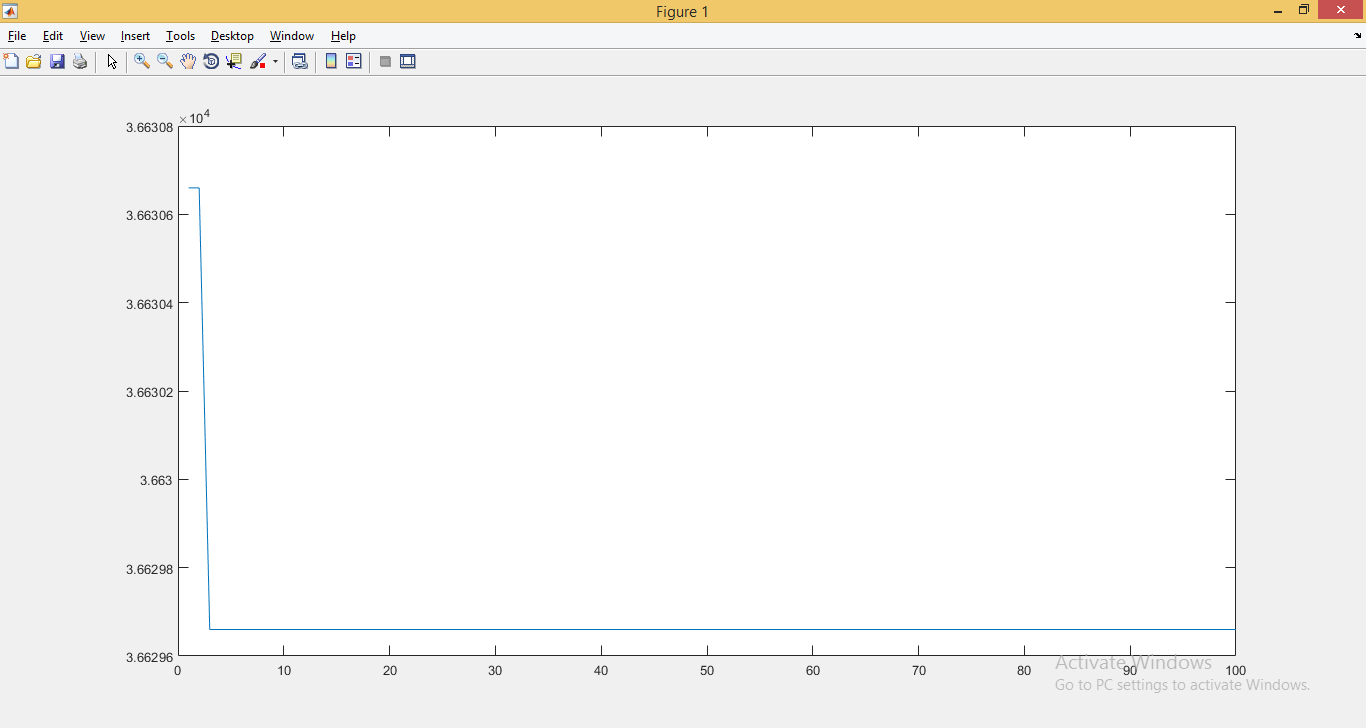
Снизил q с 1 до 0.91 за 20 тактов (за остальные 80 тактов он ничего не сделал). Слабовато, но намного сильнее, чем градиентный спуск (который снизил с 1.002 до 0.988). И крайне нестабильно.

2) Квадратичная функция.



Снизил q со 189 до 179 за 50 тактов (градиентный спуск снизил q со 140 до примерно 5). В данной ситуации Абатур показал себя нестабильным и малоэффективным.

3) Дискретная функция.



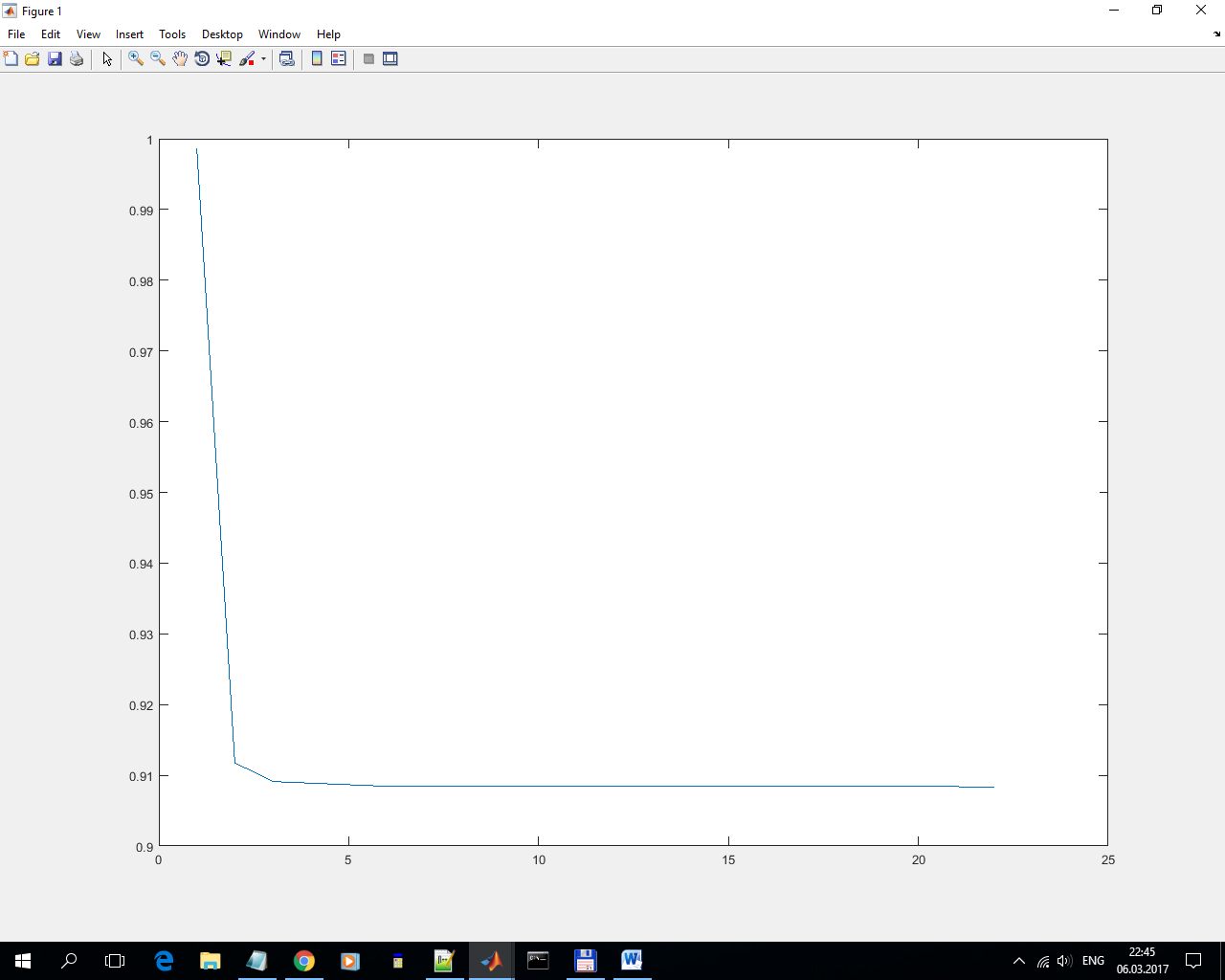
Снизил q со 3663.27 до 3662.98. Очень слабо, очень нестабильно.

Испытание 3. Абатур обученный.

Обучаем Абатур на квадратичной функции. В качестве обучающего алгоритма используем Абатур со стандартными настройками.

1) Регрессия.

Синими линиями показан процесс оптимизации до обучения. Красными – после.



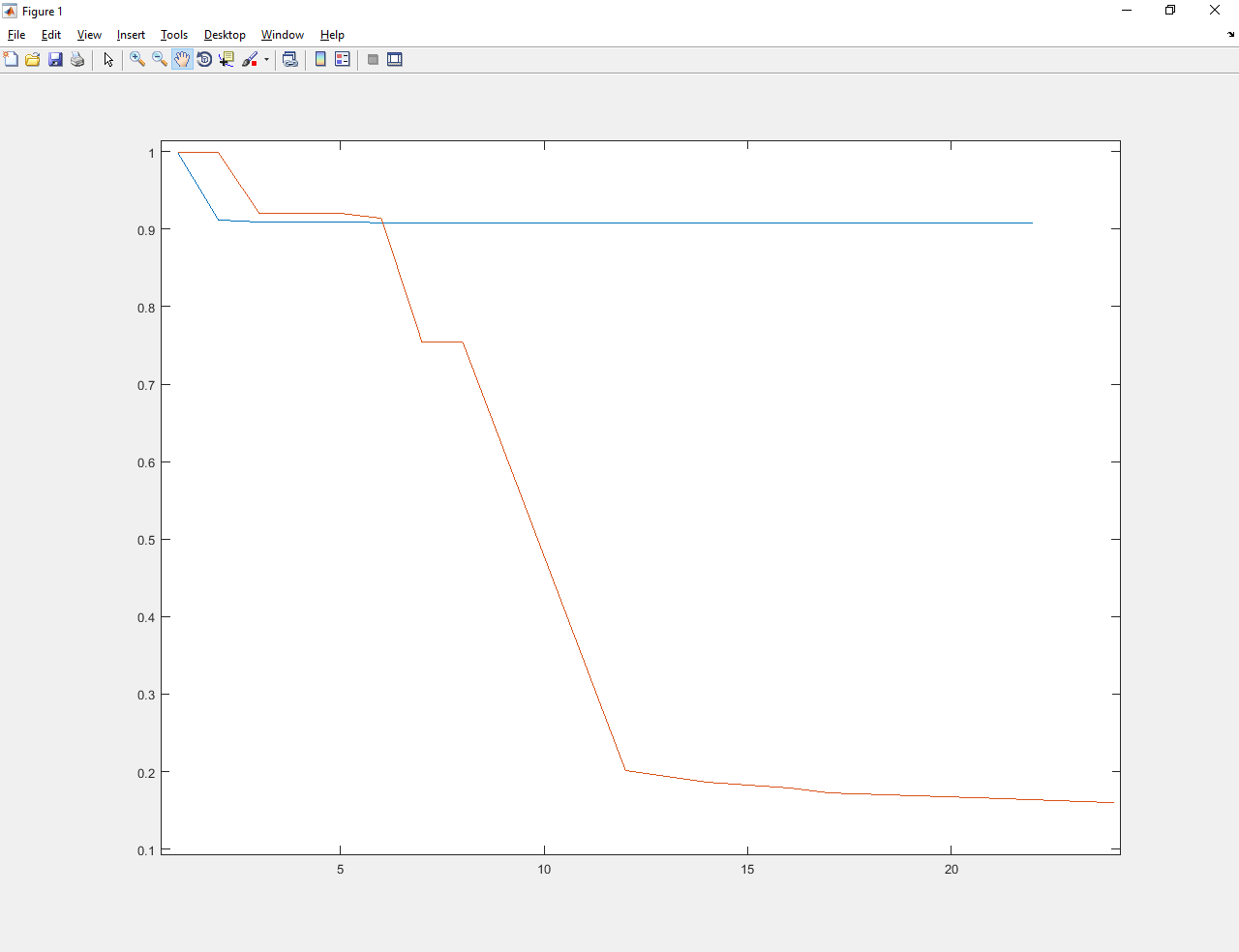
Абатур обученный улучшил значение с примерно 1 до примерно 0.17. Намного лучше и старого Абатура, и градиентного спуска.

2) Квадратичная функция.



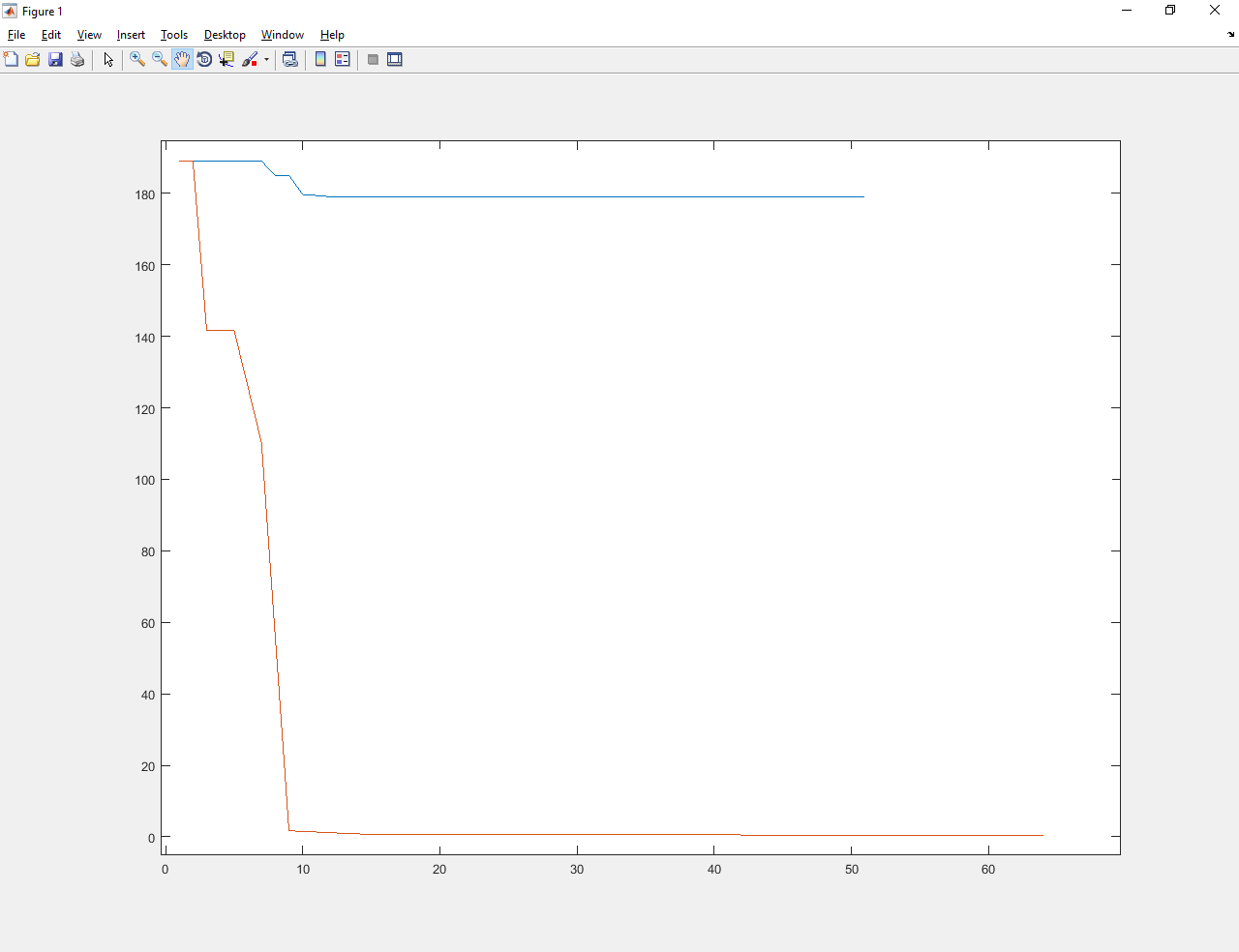
Абатур обученный улучшил значение с примерно 190 до числа меньше 1. Намного лучше и старого Абатура, и градиентного спуска.

3) Дискретная функция



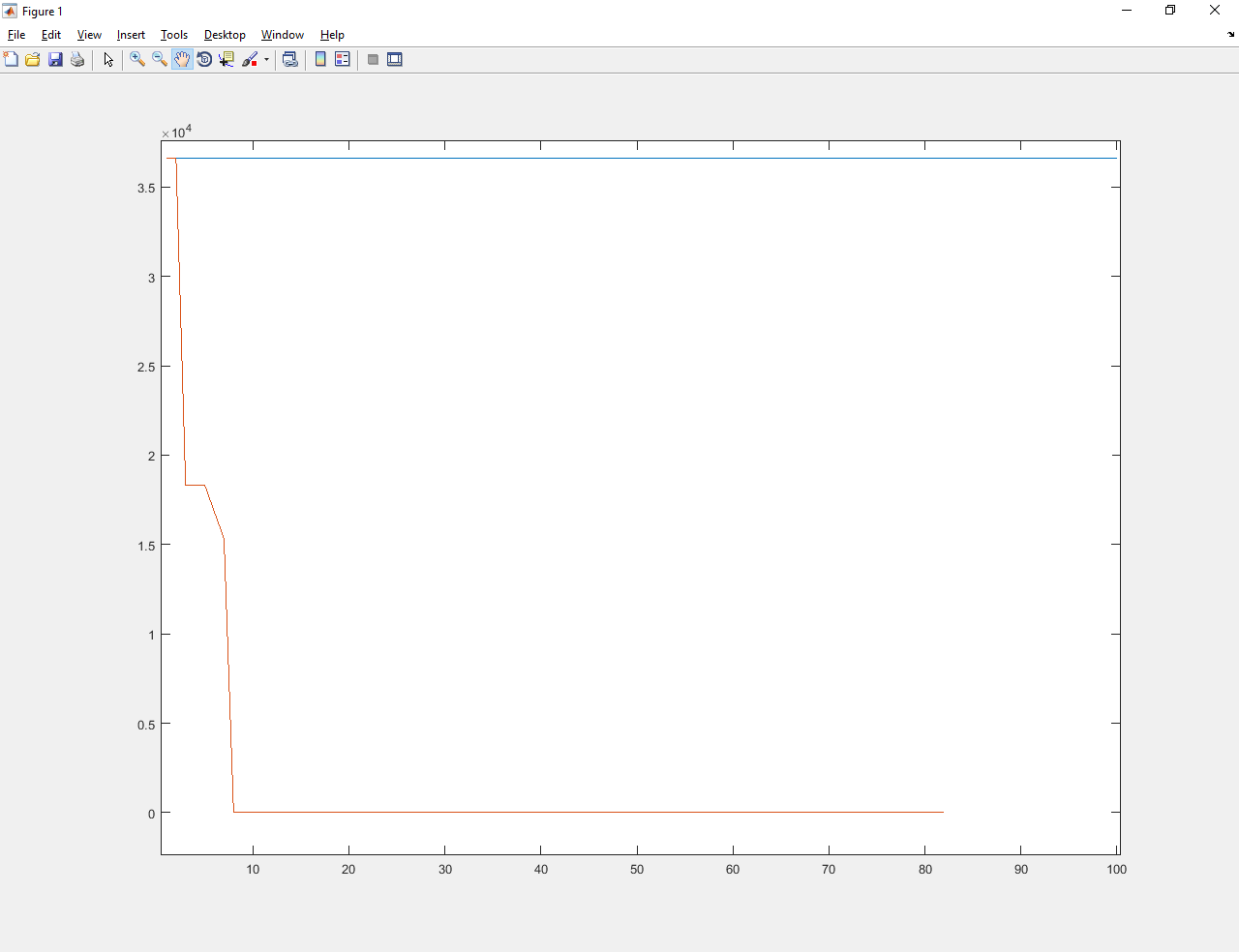
Абатур обученный улучшил значение с примерно 3600 до 0.01. Намного лучше и старого Абатура, и градиентного спуска (которые вообще не справились).

Резюме

1) Обучаемый алгоритм оптимизации создан. Оболочка для его обучения создана.
2) Я обучил Абатур на одной задаче. Он стал лучше решать все перечисленные задачи. Следовательно, алгоритм подобрал эвристики, которые в сумме пригодны для решения любой задачи из списка.

Источники литературы:

1) “Learning to learn by gradient descent by gradient descent”
2) “Metalearning”