Цель данной статьи — поделиться результатами исследования по выявлению коинтегрированных пар акций, которые представлены на Московской и Нью-Йоркской биржах, с помощью теста Энгла-Грэнджера.
Если мы возьмём две акции со стационарными приращениями, и найдём их некоторую линейную комбинацию (спред), которая будет стационарна, то такой временной ряд будет называться коинтегрированным. Наличие коинтеграции даёт нам возможность захеджироваться акциями и построить рыночно-нейтральную стратегию. Почему это возможно?
Все мы знаем, что цена акции, рассматриваемая как временной ряд, может меняться весьма значительно. Если мы будем делать позицию в какой-то одной бумаге, то в большинстве случаев это будет очень рискованная игра, так как все риски, связанные с её волатильностью, мы возьмём на себя. Однако встречаются такие акции, от которых можно ожидать, что, будучи объединёнными в пару, подобные ряды будут не слишком далеко удаляться друг от друга. Эта концепция получила название долгосрочного динамического равновесия.
В контексте стационарности долгосрочное динамическое равновесие приобретает более точную форму. Если мы возьмём стационарный ряд спреда, построенного между двумя коинтегрированными бумагами, он будет иметь свойство возврата к среднему, то есть при любом отклонении от некоторого равновесия будет стремиться вернуться обратно. На этом принципе и строится рыночно-нейтральная стратегия.
Как на фондовых рынках находить пары, связанные долгосрочным динамическим равновесием?
Первая мысль, которая приходит в голову — это вычислить корреляцию между двумя бумагами и торговать пары с сильной корреляцией. Этот подход терпит неудачу по двум причинам.
Во-первых, если бы ряды цен двух акций имели бы идеальную корреляцию, то есть если бы они изменялись в одном и том же направлении и в одной и той же пропорции, разность между рядами была бы равна нулю, и мы не смогли бы заработать никаких денег, потому что ни одна из акций никогда не будет слишком дорогой или слишком дешёвой.
Во-вторых, корреляция не даёт нам достаточной информации о взаимосвязи двух акций в долгосрочной перспективе. Например, возьмём большой и диверсифицированный портфель акций. Пусть эти акции также входят в фондовый индекс, и пусть веса акций в портфеле определяются их весами в индексе. Хотя портфель в долгосрочной перспективе должен двигаться в соответствии с индексом, будут периоды, когда акции, которые находятся в индексе, но не в портфеле, будут иметь необычные движения цен. Следовательно, эмпирические корреляции между портфелем и индексом в течение некоторого времени могут быть довольно низкими. Из-за этого при анализе мы просто отбросим такой портфель и упустим возможность заработать. Отсюда следует, что корреляция не является хорошим способом идентификации пар.
Лучше для идентификации пар использовать коинтеграцию.
Часто для обеспечения стационарности экономических рядов мы берём разности. Это приводит к следующему определению интеграции.
Временной ряд называется интегрированным порядка и обозначается , если он и его разности до порядка включительно нестационарны, а его разность порядка стационарна.
Нам для получения практических результатов потребуются только значения и . Если , то сам ряд будет стационарным, и я для краткости далее буду обозначать такие ряды . Для ряд будет нестационарным со стационарными приращениями (разностями первого порядка), и я для краткости далее буду обозначать такие ряды .
Пусть у нас есть два ряда, и . Пусть, кроме того, их линейная комбинация является В этом случае ряды и называются коинтегрированными:
По сути, коинтеграция — это регрессия нестационарных рядов. Она означает, что, если имеет нулевое среднее, то этот ряд будет редко далеко отклоняться от нуля и часто пересекать нулевой уровень. Иными словами, время от времени будет достигаться точное равновесие или близкое к нему состояние.
Мы можем рассматривать коинтеграцию не только между ценами, но и между их логарифмами. К сожалению, коинтеграция между логарифмами цен двух акций менее очевидна и интуитивно понятна, чем просто коинтеграция между ценами двух акций. Тем не менее, почему коинтеграция возможна и в случае логарифмов?
Объясняется это «гипотезой эффективного рынка», моделью ценообразования опционов и леммой Ито. На самом деле, у гипотезы эффективного рынка нет строгой формализации. Эта гипотеза предполагает, что на ликвидном рынке, где цена актива будет результатом уравновешенного спонтанного спроса и предложения, текущая цена будет точно отражать всю информацию, которая доступна игрокам на рынке. Будущие изменения в цене могут быть только результатом «новостей», которые по определению непредсказуемы, так что лучший прогноз цены на любую будущую дату — это просто цена сегодня. Другими словами, цена сегодня — это вчерашняя цена плюс случайный элемент.
Гипотеза эффективного рынка связана с основной моделью ценообразования опционов. Фундаментальное предположение этой модели заключается в том, что цена базового актива удовлетворяет процессу геометрического броуновского движения (GBM):
где и — константы, которые представляют собой, соответственно, смещение в цене актива и волатильность доходности, а — это винеровский процесс, то есть приращения независимы и нормально распределены с нулевым средним и дисперсией .
Чтобы увидеть, как уравнение GBM связано с гипотезой эффективного рынка, нужно применить к нему лемму Ито. В чём она заключается? Допустим, что значения переменной подчиняются стохастическому дифференциальному уравнению (СДУ)
где — это винеровский процесс, а и – функции, которые зависят от переменных и . Допустим также, что функция зависит от переменных и и имеет производные , , . Лемма Ито утверждает, что данная функция подчиняется уравнению
По сути, лемма Ито — это формула замены переменных в СДУ, где при определённых условиях функция от некоторого СДУ также является СДУ.
Вернёмся к уравнению GBM и преобразуем его в виде
Полагая , по лемме Ито получаем:
Введём функцию . Поскольку
получаем:
Уравнение
можно переписать в дискретном виде
где , а , то есть здесь процесс не просто стационарный, а является белым шумом. Понятие стационарного процесса шире, чем белый шум, и оно отличается тем, что стационарный процесс имеет постоянное матожидание, но оно не обязательно должно равняться нулю, как в случае с белым шумом.
Дискретную версию уравнения, приведённого выше, можно, в свою очередь, записать в виде:
Данное уравнение – это модель случайного блуждания (RW), которая обычно применяется для моделирования логарифмов цен на эффективных финансовых рынках, и которая является примером процесса. Таким образом, коинтеграция также может относиться и к логарифмам цен акций.
Несмотря на то, что некоторые скептики (в частности, я) могут сомневаться относительно адекватности описания цены акции уравнением GBM и, следовательно, возможности коинтеграции между логарифмами цен, эмпирические данные успешно развеивают этот скептицизм. Я проверяла: если коинтегрированы цены, то коинтегрированы и их логарифмы.
Первыми метод тестирования коинтеграции придумали Роберт Энгл и Клайв Грэнджэр. Они в 2003 году получили Нобелевскую премию по экономике за разработку метода коинтеграции для анализа временных рядов. Описали они его за 15 лет до премии, в 1987 году в статье «Cointegration and error correction: representation, estimation and testing».
Концептуально, для того, чтобы по имеющимся наблюдениям определить, являются ли временные ряды и коинтегрированными, нам необходимо провести тестирование нулевой гипотезы на отсутствие коинтеграции между рядами и против альтернативной гипотезы . Если нулевая гипотеза отвергается, признаётся наличие коинтеграции.
Оригинальный тест на коинтеграцию получил название теста Энгла-Грэнджера в честь его основателей. Он представляет собой двухшаговый процесс, которому предшествует проверка и на интегрируемость первого порядка, и . Мы это подробно обсуждали в статье про стационарные приращения. По сути, там описаны все подготовительные работы, которые необходимо сделать до того, как приступить непосредственно к тесту Энгла-Грэнджера. Допустим, мы это сделали.
Ряды и являются коинтегрированными, если их спред , то есть является стационарным. Первый шаг в тесте Энгла-Грэнджера заключается в получении состоятельной оценки . Это делается с помощью применения МНК (метода наименьших квадратов) для линейной регрессии к уравнению . Второй шаг заключается в проверке на стационарность остатков , полученных при МНК-оценивании коинтеграционного уравнения.
Обычно стационарность мы проверяем тестом Дики-Фуллера. Однако в 1990 году Филлипс и Улиарис в статье «Asymptotic properties of residual based tests for cointegration» показали, что к проверке ряда нельзя применять тест Дики-Фуллера.
Дело в том, что МНК «выбирает» остатки так, чтобы они имели наименьшую возможную вариацию, поэтому, даже если переменные не коинтегрированы, МНК делает остатки «похожими» на стационарные. Из-за этого при использовании теста Дики-Фуллера гипотеза нестационарности отвергается слишком часто и, соответственно, ошибочно принимается гипотеза наличия коинтеграции.
Если мы изучим статью авторов, то увидим, что в приложении они дают таблицы с критическими значениями, однако они оказались довольно неточными. Позднее, в 1991 году, Энгл и Грэнджер издали книжку «Long-Run Economic Relationship». В ней в 13-ой главе под названием «Critical value for cointegration tests» МакКиннон привёл уточнённые асимптотические критические значения -статистики, которые были получены имитационным моделированием и подходят для данного случая.
В 1993 году МакКиннон вместе с Дэвидсоном издали свою книжку «Estimation and Inference in Econometrics», где тоже привели уточнённые критические значения. Таким образом, если (остатки стационарны), то (спред тоже стационарен), что означает наличие коинтеграции между и .
В общем, метод Энгла-Грэнджера сводится к:
В стандартных пакетах типа матлаба этот тест уже написан, давайте им воспользуемся.
Итак, у нас есть два ряда цен акций, и . Мы хотим, чтобы и были коинтегрированными, то есть чтобы спред был стационарным. Если мы хотим получить стационарный ряд с нулевым средним, то можем включить постоянную в уравнение, так что спред будет выглядеть как .
Начнём с результатов, полученных на Московской бирже, которые я описывала в статье про стационарные приращения. Там я нашла пять рядов. Составим из них всевозможные комбинации и проверим на коинтеграцию с помощью теста Энгла-Грэнджера.
Сначала выберем из базы данных Microsoft SQL Server, в которой я храню спарсенные с Московской биржи значения цен акций, нужные нам бумаги и импортируем их в виде массива:
В этом массиве для четырёх из пяти акций есть данные с января за 252 торговых дня. Однако, для одной из акций сделки начали совершаться только в феврале, так что данные есть только за 215 торговых дней. Нам критически важно, чтобы у всех акций массив цен был одинаковой длины, поэтому в таких ситуациях у нас есть два варианта.
Первый вариант — исключить акцию с коротким массивом цен из эксперимента и использовать максимальное количество измерений цены для того, чтобы получить более точные результаты. Второй вариант — пожертвовать частью данных и включить все акции в угоду большей практичности. Я проводила оба эксперимента, и в данном случае разницы в результатах никакой не было, поэтому давайте просто обрежем январские данные:
Тест Энгла-Грэнджера выполняется с помощью функции egcitest, которая на вход принимает массив из временных рядов, в данном случае размера , где — количество торговых дней. На выходе функция возвращает логическое значение, равное 1, если нулевая гипотеза отвергается в пользу альтернативной, и 0 – иначе.
Следующая задача, которую нам надо решить, — какую акцию принять за , а какую — за . По-хорошему, надо попробовать и то, и другое, а затем сравнить тестовые статистики. В большинстве случаев, будет существовать как прямая, так и обратная регрессия. Давайте начнём со случая, когда .
Составим все возможные пары из пяти выявленных рядов и выполним тест Энгла-Грэнджера как для регрессии со свободным членом (по умолчанию), так и без него (задаётся аргументом 'creg' со значением 'nc'):
В случае регрессии со свободным членом программа два раза отвергает нулевую гипотезу в пользу альтернативной модели, выявляя коинтегрированные пары акций с тикерами (NKHP, VTRS), (NKHP, ZHIV). В случае регрессии без свободного члена программа один раз отвергает нулевую гипотезу в пользу альтернативной, выявляя коинтегрированную пару акций с тикерами (VSYDP, NKHP).
В случае обратной регрессии () со свободным членом программа два раза отвергает нулевую гипотезу в пользу альтернативной модели, выявляя коинтегрированные пары акций с тикерами (VTRS, NKHP), (ZHIV, NKHP). В случае регрессии без свободного члена программа четыре раза отвергает нулевую гипотезу в пользу альтернативной, выявляя коинтегрированные пары акций с тикерами (GRNT, VTRS), (GRNT, VSYDP), (GRNT, ZHIV), (GRNT, NKHP).
Давайте оценим значения и , которые могут быть получены в качестве возвращаемых значений функции egcitest, и нарисуем спред:
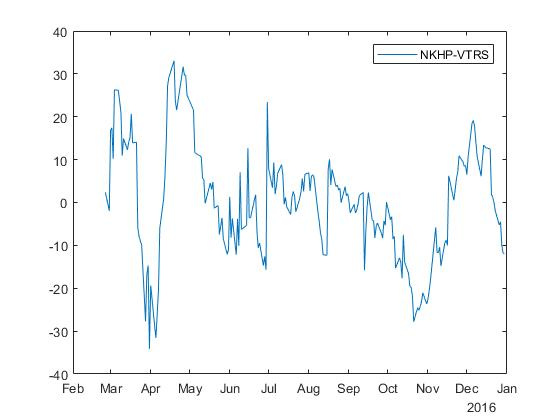
Для акций с тикерами NKHP и VTRS получаем спред с коэффициентами и :
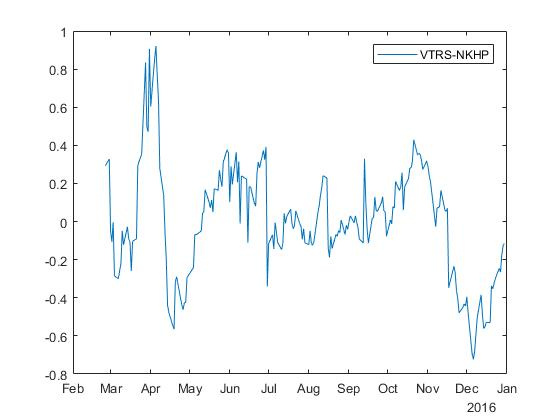
Для обратной регрессии получаем «зеркальный» спред с коэффициентами и :
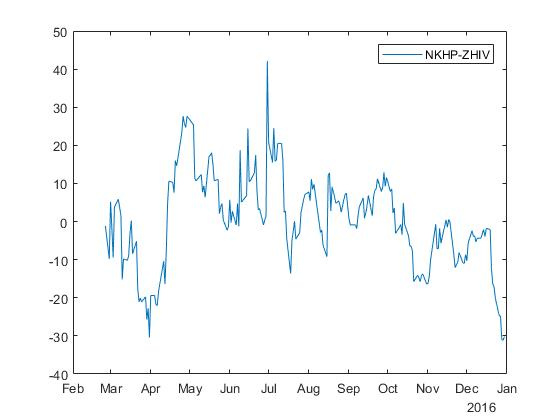
Для акций с тикерами NKHP and ZHIV получаем спред с коэффициентами и :
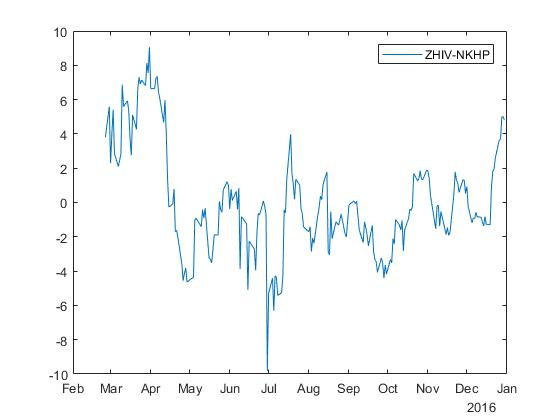
Для обратной регрессии получаем спред с коэффициентами и :
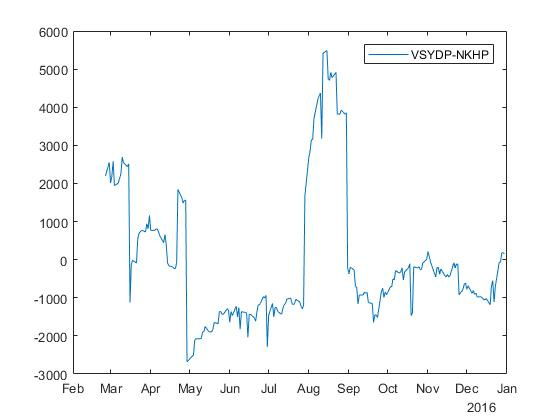
Для акций с тикерами VSYDP and NKHP получаем спред с коэффициентом :
Аналогичные эксперименты были проведены для акций Нью-Йоркской фондовой биржи (NYSE). В результате для прямой регрессии было получено 158 коинтегрированных пар в случае регрессии со свободным членом и 130 коинтегрированных пар в случае регрессии без свободного члена. Для обратной регрессии было получено 170 коинтегрированных пар в случае регрессии со свободным членом и 144 коинтегрированные пары в случае регрессии без свободного члена.
Давайте посмотрим на регрессионную статистику коинтегрированной регрессии для пары (NKHP, VTRS).
Тестовая статистика как в прямой, так и в обратной регрессии говорит нам, что переменная в данном случае незначима (). Это означает, что цена может быть слабо экзогенной, даже несмотря на то, что переменные коинтегрированы.
Для применения критерия Стьюдента и критерия Фишера необходимо, чтобы статистика имела нормальное распределение. В нашем случае, статистика имеет распределение, подобное тому, что было установлено Дики и Фуллером (о нём я тоже писала в статье про стационарные приращения), поэтому расчётные значения этих статистик будут довольно большими и ничего содержательного нам не скажут.
Статистика Дарбина-Уотсона приемлемая (при положительной автокорреляции статистика стремится к нулю). В случае обратной регрессии она немного лучше, чем в случае прямой.
Коэффициент детерминации приемлемый (для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%). Судя по этому критерию, никакой разницы между прямой и обратной регрессией нет.
Судя по информационным критериям, обратная регрессия сильно выигрывает перед прямой (считается, что наилучшей будет модель с наименьшим значением критерия).
Посмотрим на регрессионную статистику коинтегрированной регрессии для пары (NKHP, ZHIV).
Тестовая статистика как в прямой, так и в обратной регрессии говорит нам, что переменная в данном случае незначима. Статистика Дарбина-Уотсона приемлемая, в случае обратной регрессии немного лучше, чем в случае прямой. Коэффициент детерминации приемлемый, разницы между прямой и обратной регрессией не наблюдается. По информационным критериям, обратная регрессия немного выигрывает перед прямой.
Регрессионная статистика коинтегрированной регрессии для пары (VSYDP, NKHP).
Переменная , судя по тестовой статистике, опять незначима. Критерий Фишера улетел в космос. Статистика Дарбина-Уотсона приемлемая. Коэффициент детерминации маленький, поэтому модель считается плохой.
На фондовых рынках существует достаточное количество коинтегрированных акций, то есть таких, что их спред представляет собой стационарный процесс. Наличие таких пар даёт почву для дальнейших исследований и стабильного извлечения прибыли, но о конкретных стратегиях мы поговорим в следующий раз.
Роберт Ф. Энгл, К. У. Дж. Грэнджер. Коинтеграция и коррекция ошибок: представление, оценивание и тестирование // Прикладная эконометрика. — 2015. — 39 (3). — С. 107-135.
Это перевод оригинальной статьи авторов 1987 года, там более подробно изложено определение коинтеграции. Также можно продолжать читать Магнуса, которого я рекомендовала в статье про стационарные приращения, там тоже есть раздел про коинтеграцию.
Если мы возьмём две акции со стационарными приращениями, и найдём их некоторую линейную комбинацию (спред), которая будет стационарна, то такой временной ряд будет называться коинтегрированным. Наличие коинтеграции даёт нам возможность захеджироваться акциями и построить рыночно-нейтральную стратегию. Почему это возможно?
Принцип, на котором строится извлечение прибыли
Все мы знаем, что цена акции, рассматриваемая как временной ряд, может меняться весьма значительно. Если мы будем делать позицию в какой-то одной бумаге, то в большинстве случаев это будет очень рискованная игра, так как все риски, связанные с её волатильностью, мы возьмём на себя. Однако встречаются такие акции, от которых можно ожидать, что, будучи объединёнными в пару, подобные ряды будут не слишком далеко удаляться друг от друга. Эта концепция получила название долгосрочного динамического равновесия.
В контексте стационарности долгосрочное динамическое равновесие приобретает более точную форму. Если мы возьмём стационарный ряд спреда, построенного между двумя коинтегрированными бумагами, он будет иметь свойство возврата к среднему, то есть при любом отклонении от некоторого равновесия будет стремиться вернуться обратно. На этом принципе и строится рыночно-нейтральная стратегия.
Как на фондовых рынках находить пары, связанные долгосрочным динамическим равновесием?
Корреляция
Первая мысль, которая приходит в голову — это вычислить корреляцию между двумя бумагами и торговать пары с сильной корреляцией. Этот подход терпит неудачу по двум причинам.
Во-первых, если бы ряды цен двух акций имели бы идеальную корреляцию, то есть если бы они изменялись в одном и том же направлении и в одной и той же пропорции, разность между рядами была бы равна нулю, и мы не смогли бы заработать никаких денег, потому что ни одна из акций никогда не будет слишком дорогой или слишком дешёвой.
Во-вторых, корреляция не даёт нам достаточной информации о взаимосвязи двух акций в долгосрочной перспективе. Например, возьмём большой и диверсифицированный портфель акций. Пусть эти акции также входят в фондовый индекс, и пусть веса акций в портфеле определяются их весами в индексе. Хотя портфель в долгосрочной перспективе должен двигаться в соответствии с индексом, будут периоды, когда акции, которые находятся в индексе, но не в портфеле, будут иметь необычные движения цен. Следовательно, эмпирические корреляции между портфелем и индексом в течение некоторого времени могут быть довольно низкими. Из-за этого при анализе мы просто отбросим такой портфель и упустим возможность заработать. Отсюда следует, что корреляция не является хорошим способом идентификации пар.
Лучше для идентификации пар использовать коинтеграцию.
Коинтеграция
Часто для обеспечения стационарности экономических рядов мы берём разности. Это приводит к следующему определению интеграции.
Временной ряд называется интегрированным порядка и обозначается , если он и его разности до порядка включительно нестационарны, а его разность порядка стационарна.
Нам для получения практических результатов потребуются только значения и . Если , то сам ряд будет стационарным, и я для краткости далее буду обозначать такие ряды . Для ряд будет нестационарным со стационарными приращениями (разностями первого порядка), и я для краткости далее буду обозначать такие ряды .
Пусть у нас есть два ряда, и . Пусть, кроме того, их линейная комбинация является В этом случае ряды и называются коинтегрированными:
По сути, коинтеграция — это регрессия нестационарных рядов. Она означает, что, если имеет нулевое среднее, то этот ряд будет редко далеко отклоняться от нуля и часто пересекать нулевой уровень. Иными словами, время от времени будет достигаться точное равновесие или близкое к нему состояние.
Коинтеграция логарифмов цен
Мы можем рассматривать коинтеграцию не только между ценами, но и между их логарифмами. К сожалению, коинтеграция между логарифмами цен двух акций менее очевидна и интуитивно понятна, чем просто коинтеграция между ценами двух акций. Тем не менее, почему коинтеграция возможна и в случае логарифмов?
Объясняется это «гипотезой эффективного рынка», моделью ценообразования опционов и леммой Ито. На самом деле, у гипотезы эффективного рынка нет строгой формализации. Эта гипотеза предполагает, что на ликвидном рынке, где цена актива будет результатом уравновешенного спонтанного спроса и предложения, текущая цена будет точно отражать всю информацию, которая доступна игрокам на рынке. Будущие изменения в цене могут быть только результатом «новостей», которые по определению непредсказуемы, так что лучший прогноз цены на любую будущую дату — это просто цена сегодня. Другими словами, цена сегодня — это вчерашняя цена плюс случайный элемент.
Гипотеза эффективного рынка связана с основной моделью ценообразования опционов. Фундаментальное предположение этой модели заключается в том, что цена базового актива удовлетворяет процессу геометрического броуновского движения (GBM):
где и — константы, которые представляют собой, соответственно, смещение в цене актива и волатильность доходности, а — это винеровский процесс, то есть приращения независимы и нормально распределены с нулевым средним и дисперсией .
Чтобы увидеть, как уравнение GBM связано с гипотезой эффективного рынка, нужно применить к нему лемму Ито. В чём она заключается? Допустим, что значения переменной подчиняются стохастическому дифференциальному уравнению (СДУ)
где — это винеровский процесс, а и – функции, которые зависят от переменных и . Допустим также, что функция зависит от переменных и и имеет производные , , . Лемма Ито утверждает, что данная функция подчиняется уравнению
По сути, лемма Ито — это формула замены переменных в СДУ, где при определённых условиях функция от некоторого СДУ также является СДУ.
Вернёмся к уравнению GBM и преобразуем его в виде
Полагая , по лемме Ито получаем:
Введём функцию . Поскольку
получаем:
Уравнение
можно переписать в дискретном виде
где , а , то есть здесь процесс не просто стационарный, а является белым шумом. Понятие стационарного процесса шире, чем белый шум, и оно отличается тем, что стационарный процесс имеет постоянное матожидание, но оно не обязательно должно равняться нулю, как в случае с белым шумом.
Дискретную версию уравнения, приведённого выше, можно, в свою очередь, записать в виде:
Данное уравнение – это модель случайного блуждания (RW), которая обычно применяется для моделирования логарифмов цен на эффективных финансовых рынках, и которая является примером процесса. Таким образом, коинтеграция также может относиться и к логарифмам цен акций.
Несмотря на то, что некоторые скептики (в частности, я) могут сомневаться относительно адекватности описания цены акции уравнением GBM и, следовательно, возможности коинтеграции между логарифмами цен, эмпирические данные успешно развеивают этот скептицизм. Я проверяла: если коинтегрированы цены, то коинтегрированы и их логарифмы.
Тестирование коинтеграции
Первыми метод тестирования коинтеграции придумали Роберт Энгл и Клайв Грэнджэр. Они в 2003 году получили Нобелевскую премию по экономике за разработку метода коинтеграции для анализа временных рядов. Описали они его за 15 лет до премии, в 1987 году в статье «Cointegration and error correction: representation, estimation and testing».
Концептуально, для того, чтобы по имеющимся наблюдениям определить, являются ли временные ряды и коинтегрированными, нам необходимо провести тестирование нулевой гипотезы на отсутствие коинтеграции между рядами и против альтернативной гипотезы . Если нулевая гипотеза отвергается, признаётся наличие коинтеграции.
Оригинальный тест на коинтеграцию получил название теста Энгла-Грэнджера в честь его основателей. Он представляет собой двухшаговый процесс, которому предшествует проверка и на интегрируемость первого порядка, и . Мы это подробно обсуждали в статье про стационарные приращения. По сути, там описаны все подготовительные работы, которые необходимо сделать до того, как приступить непосредственно к тесту Энгла-Грэнджера. Допустим, мы это сделали.
Ряды и являются коинтегрированными, если их спред , то есть является стационарным. Первый шаг в тесте Энгла-Грэнджера заключается в получении состоятельной оценки . Это делается с помощью применения МНК (метода наименьших квадратов) для линейной регрессии к уравнению . Второй шаг заключается в проверке на стационарность остатков , полученных при МНК-оценивании коинтеграционного уравнения.
Обычно стационарность мы проверяем тестом Дики-Фуллера. Однако в 1990 году Филлипс и Улиарис в статье «Asymptotic properties of residual based tests for cointegration» показали, что к проверке ряда нельзя применять тест Дики-Фуллера.
Дело в том, что МНК «выбирает» остатки так, чтобы они имели наименьшую возможную вариацию, поэтому, даже если переменные не коинтегрированы, МНК делает остатки «похожими» на стационарные. Из-за этого при использовании теста Дики-Фуллера гипотеза нестационарности отвергается слишком часто и, соответственно, ошибочно принимается гипотеза наличия коинтеграции.
Если мы изучим статью авторов, то увидим, что в приложении они дают таблицы с критическими значениями, однако они оказались довольно неточными. Позднее, в 1991 году, Энгл и Грэнджер издали книжку «Long-Run Economic Relationship». В ней в 13-ой главе под названием «Critical value for cointegration tests» МакКиннон привёл уточнённые асимптотические критические значения -статистики, которые были получены имитационным моделированием и подходят для данного случая.
В 1993 году МакКиннон вместе с Дэвидсоном издали свою книжку «Estimation and Inference in Econometrics», где тоже привели уточнённые критические значения. Таким образом, если (остатки стационарны), то (спред тоже стационарен), что означает наличие коинтеграции между и .
В общем, метод Энгла-Грэнджера сводится к:
- оценке с помощью МНК;
- вычислению спреда и тестированию на стационарность с помощью уточнённых критических значений.
В стандартных пакетах типа матлаба этот тест уже написан, давайте им воспользуемся.
Тестирование коинтеграции в MATLAB
Итак, у нас есть два ряда цен акций, и . Мы хотим, чтобы и были коинтегрированными, то есть чтобы спред был стационарным. Если мы хотим получить стационарный ряд с нулевым средним, то можем включить постоянную в уравнение, так что спред будет выглядеть как .
Начнём с результатов, полученных на Московской бирже, которые я описывала в статье про стационарные приращения. Там я нашла пять рядов. Составим из них всевозможные комбинации и проверим на коинтеграцию с помощью теста Энгла-Грэнджера.
Сначала выберем из базы данных Microsoft SQL Server, в которой я храню спарсенные с Московской биржи значения цен акций, нужные нам бумаги и импортируем их в виде массива:
conn = database.ODBCConnection('uXXXXXX.mssql.masterhost.ru', 'uXXXXXX', 'XXXXXXXXXX');
curs = exec(conn, 'SELECT ALL PriceId, StockId, Date, Price FROM StockPrices WHERE StockId IN (52, 55, 67, 75, 162) AND Date >= ''2016-01-01 00:00:00.000'' AND Date < ''2017-01-01 00:00:00.000''');
curs = fetch(curs);
data = curs.Data
sqlquery = 'SELECT ALL StockId, ShortName, Code FROM Stocks WHERE StockId IN (52, 55, 67, 75, 162)';
curs = exec(conn, sqlquery);
curs = fetch(curs);
names = curs.Data
close(conn);
В этом массиве для четырёх из пяти акций есть данные с января за 252 торговых дня. Однако, для одной из акций сделки начали совершаться только в феврале, так что данные есть только за 215 торговых дней. Нам критически важно, чтобы у всех акций массив цен был одинаковой длины, поэтому в таких ситуациях у нас есть два варианта.
Первый вариант — исключить акцию с коротким массивом цен из эксперимента и использовать максимальное количество измерений цены для того, чтобы получить более точные результаты. Второй вариант — пожертвовать частью данных и включить все акции в угоду большей практичности. Я проводила оба эксперимента, и в данном случае разницы в результатах никакой не было, поэтому давайте просто обрежем январские данные:
dates = unique(datetime(data(:,3)));
% Cut dates array until price of stock with StockId=67 is not empty.
dates(1:37,:) = [];
prices = zeros(length(dates),length(names));
for i = 1:length(names)
% Indexes with current stock's data
indexes = find(cell2mat(data(:,2)) == cell2mat(names(i,1)));
if length(indexes) == 252
indexes(1:37,:) = [];
end
for j=1:length(dates)
% Fill prices according to date
prices(j,i) = cell2mat(data(indexes(j),4));
end
end
Тест Энгла-Грэнджера выполняется с помощью функции egcitest, которая на вход принимает массив из временных рядов, в данном случае размера , где — количество торговых дней. На выходе функция возвращает логическое значение, равное 1, если нулевая гипотеза отвергается в пользу альтернативной, и 0 – иначе.
Следующая задача, которую нам надо решить, — какую акцию принять за , а какую — за . По-хорошему, надо попробовать и то, и другое, а затем сравнить тестовые статистики. В большинстве случаев, будет существовать как прямая, так и обратная регрессия. Давайте начнём со случая, когда .
Составим все возможные пары из пяти выявленных рядов и выполним тест Энгла-Грэнджера как для регрессии со свободным членом (по умолчанию), так и без него (задаётся аргументом 'creg' со значением 'nc'):
isCoint = zeros(length(nchoosek(names(:,1),2)), 3);
k=1;
for i=1:length(names)
for j=i+1:length(names)
if mean(prices(:,i)) < mean(prices(:,j))
isCoint(k,1) = cell2mat(names(j,1));
isCoint(k,2) = cell2mat(names(i,1));
testPrices(:,1) = prices(:,j);
testPrices(:,2) = prices(:,i);
else
isCoint(k,1) = cell2mat(names(i,1));
isCoint(k,2) = cell2mat(names(j,1));
testPrices(:,1) = prices(:,i);
testPrices(:,2) = prices(:,j);
end
isCoint(k,3) = egcitest(testPrices);
isCoint(k,4) = egcitest(testPrices, 'creg', 'nc');
k = k + 1;
end
end
В случае регрессии со свободным членом программа два раза отвергает нулевую гипотезу в пользу альтернативной модели, выявляя коинтегрированные пары акций с тикерами (NKHP, VTRS), (NKHP, ZHIV). В случае регрессии без свободного члена программа один раз отвергает нулевую гипотезу в пользу альтернативной, выявляя коинтегрированную пару акций с тикерами (VSYDP, NKHP).
В случае обратной регрессии () со свободным членом программа два раза отвергает нулевую гипотезу в пользу альтернативной модели, выявляя коинтегрированные пары акций с тикерами (VTRS, NKHP), (ZHIV, NKHP). В случае регрессии без свободного члена программа четыре раза отвергает нулевую гипотезу в пользу альтернативной, выявляя коинтегрированные пары акций с тикерами (GRNT, VTRS), (GRNT, VSYDP), (GRNT, ZHIV), (GRNT, NKHP).
Давайте оценим значения и , которые могут быть получены в качестве возвращаемых значений функции egcitest, и нарисуем спред:
% NKHP and VTRS
indexY = 5;
indexX = 1;
testPrices(:,1) = prices(:,indexY);
testPrices(:,2) = prices(:,indexX);
[h,pValue,stat,cValue,reg1,reg2] = egcitest(testPrices);
alpha = reg1.coeff(1);
beta = reg1.coeff(2);
spread = reg1.res;
plot(dates,spread)
legend(strcat(names(indexY,3),'-',names(indexX,3)));
Для акций с тикерами NKHP и VTRS получаем спред с коэффициентами и :

Для обратной регрессии получаем «зеркальный» спред с коэффициентами и :

Для акций с тикерами NKHP and ZHIV получаем спред с коэффициентами и :

Для обратной регрессии получаем спред с коэффициентами и :

Для акций с тикерами VSYDP and NKHP получаем спред с коэффициентом :

Аналогичные эксперименты были проведены для акций Нью-Йоркской фондовой биржи (NYSE). В результате для прямой регрессии было получено 158 коинтегрированных пар в случае регрессии со свободным членом и 130 коинтегрированных пар в случае регрессии без свободного члена. Для обратной регрессии было получено 170 коинтегрированных пар в случае регрессии со свободным членом и 144 коинтегрированные пары в случае регрессии без свободного члена.
Регрессионная статистика
Давайте посмотрим на регрессионную статистику коинтегрированной регрессии для пары (NKHP, VTRS).
| Статистика | Прямая регрессия | Обратная регрессия |
|---|---|---|
| Коэффициенты | , | , |
| Тестовая статистика | , | , |
| -статистика | , | , |
| -статистика | 482,9196 | 482,9196 |
| Статистика Дарбина-Уотсона | 0,2548 | 0,2203 |
| Коэффициент детерминации | 0,6939 | 0,6939 |
| Скорректированный коэффициент детерминации | 0,6925 | 0,6925 |
| Информационный критерий Акаике | 1726,5 | 88,8336 |
| Баесовский информационный критерий Шварца | 1733,2 | 95,5748 |
| Информационный критерий Ханнана-Куинна | 1729,2 | 91,5574 |
Тестовая статистика как в прямой, так и в обратной регрессии говорит нам, что переменная в данном случае незначима (). Это означает, что цена может быть слабо экзогенной, даже несмотря на то, что переменные коинтегрированы.
Для применения критерия Стьюдента и критерия Фишера необходимо, чтобы статистика имела нормальное распределение. В нашем случае, статистика имеет распределение, подобное тому, что было установлено Дики и Фуллером (о нём я тоже писала в статье про стационарные приращения), поэтому расчётные значения этих статистик будут довольно большими и ничего содержательного нам не скажут.
Статистика Дарбина-Уотсона приемлемая (при положительной автокорреляции статистика стремится к нулю). В случае обратной регрессии она немного лучше, чем в случае прямой.
Коэффициент детерминации приемлемый (для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%). Судя по этому критерию, никакой разницы между прямой и обратной регрессией нет.
Судя по информационным критериям, обратная регрессия сильно выигрывает перед прямой (считается, что наилучшей будет модель с наименьшим значением критерия).
Посмотрим на регрессионную статистику коинтегрированной регрессии для пары (NKHP, ZHIV).
| Статистика | Прямая регрессия | Обратная регрессия |
|---|---|---|
| Коэффициенты | и | и |
| Тестовая статистика | , | , |
| -статистика | , | , |
| -статистика | 592,652 | 592,652 |
| Статистика Дарбина-Уотсона | 0,2614 | 0,2104 |
| Коэффициент детерминации | 0,7356 | 0,7356 |
| Скорректированный коэффициент детерминации | 0,7344 | 0,7344 |
| Информационный критерий Акаике | 1695 | 1108,8 |
| Баесовский информационный критерий Шварца | 1701,7 | 1115,5 |
| Информационный критерий Ханнана-Куинна | 1697,7 | 1111,5 |
Тестовая статистика как в прямой, так и в обратной регрессии говорит нам, что переменная в данном случае незначима. Статистика Дарбина-Уотсона приемлемая, в случае обратной регрессии немного лучше, чем в случае прямой. Коэффициент детерминации приемлемый, разницы между прямой и обратной регрессией не наблюдается. По информационным критериям, обратная регрессия немного выигрывает перед прямой.
Регрессионная статистика коинтегрированной регрессии для пары (VSYDP, NKHP).
| Статистика | Прямая регрессия |
|---|---|
| Коэффициенты | |
| Тестовая статистика | , |
| -статистика | 82,5035 |
| -статистика | |
| Статистика Дарбина-Уотсона | 0,1305 |
| Коэффициент детерминации | 0,1928 |
| Скорректированный коэффициент детерминации | 0,1928 |
| Информационный критерий Акаике | 3823,8 |
| Баесовский информационный критерий Шварца | 3827,1 |
| Информационный критерий Ханнана-Куинна | 3825,1 |
Переменная , судя по тестовой статистике, опять незначима. Критерий Фишера улетел в космос. Статистика Дарбина-Уотсона приемлемая. Коэффициент детерминации маленький, поэтому модель считается плохой.
Выводы
На фондовых рынках существует достаточное количество коинтегрированных акций, то есть таких, что их спред представляет собой стационарный процесс. Наличие таких пар даёт почву для дальнейших исследований и стабильного извлечения прибыли, но о конкретных стратегиях мы поговорим в следующий раз.
Что почитать по теме?
Роберт Ф. Энгл, К. У. Дж. Грэнджер. Коинтеграция и коррекция ошибок: представление, оценивание и тестирование // Прикладная эконометрика. — 2015. — 39 (3). — С. 107-135.
Это перевод оригинальной статьи авторов 1987 года, там более подробно изложено определение коинтеграции. Также можно продолжать читать Магнуса, которого я рекомендовала в статье про стационарные приращения, там тоже есть раздел про коинтеграцию.
Поделиться с друзьями


frees2
В двух словах, всё это, следить с помощью одних акций за другими.