
Снежинки различных форм и размеров, появившиеся в естественной среде. Фотография из журнала Popular Science Monthly Volume № 53 от 1898 г.
Возможно, вы слышали поговорку об «особенной снежинке». Речь идёт о том, что снежинки красивы и ценны тем, поскольку в огромном их количестве нельзя найти двух одинаковых. Говорят, что не существует двух идентичных снежинок – но так ли это на самом деле? Стоит обратиться к тому, что думает по этому поводу наука – именно об этом и спрашивает нас один из наших читателей:
Я слышала, что учёные говорят, будто не существует двух одинаковых снежинок. А я скажу: откуда это может быть точно известно, если только вы не изучите все упавшие на землю снежинки? Может быть, где-нибудь в России снежинка падает одновременно с идентичной ей снежинкой где-нибудь в Миннесоте.
Чтобы рассмотреть этот вопрос с научной точки зрения, нужно понять, как получается снежинка и насколько вероятно получение двух одинаковых снежинок.
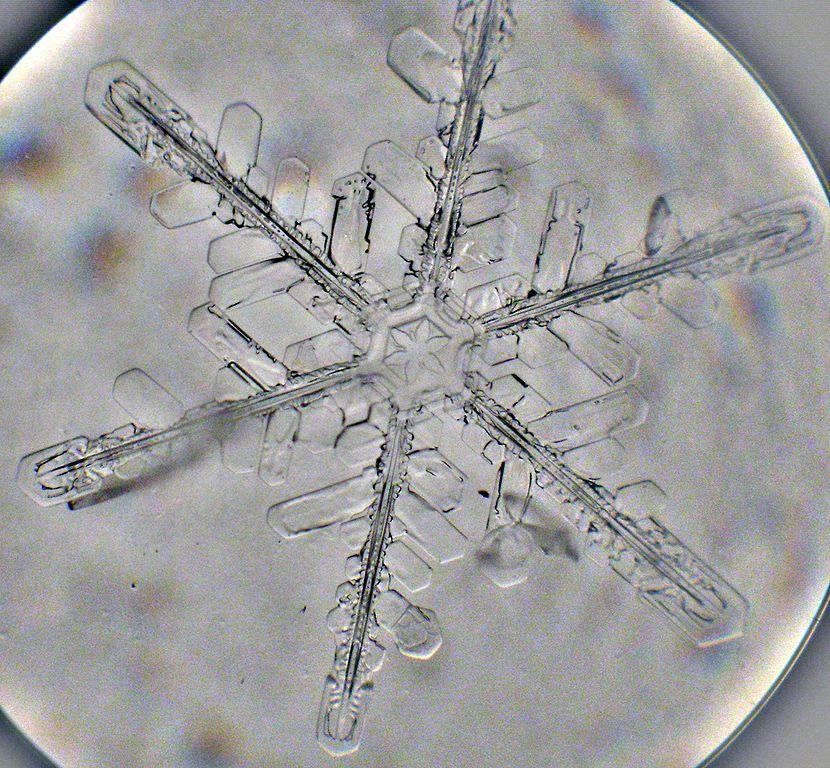
Снежинка под оптическим микроскопом
Снежинка – это молекулы воды, связанные вместе в определённой твёрдой конфигурации. У большинства из них наблюдается шестиугольная симметрия; это происходит из-за того, под каким углом молекулы воды способны связываться друг с другом. Этот угол определяется физикой атома кислорода, двух атомов водорода и электромагнитного взаимодействия. Простейший из микроскопических снежных кристаллов, который можно увидеть в оптический микроскоп, имеет размер в одну миллионную метра (1 мкм) и может принимать весьма простые формы – к примеру, плоского шестиугольника. В нём умещается всего около 10000 атомов, и среди них можно найти множество одинаковых.

Шестиугольность симметрии снежинок известна давно. Эта коллекция фотографий датируется 1902-м годом.
Согласно Книге рекордов Гиннеса, Нэнси Найт, учёный из Национального центра атмосферных исследований, повезло обнаружить две одинаковые снежинки во время исследований снежных кристаллов из метели в Висконсине 1988 года с использованием микроскопа. Но Гиннес выдаёт сертификат только на основании идентичности снежинок с учётом точности, доступной микроскопу. Когда физика требует идентичность двух объектов, она имеет в виду идентичность вплоть до субатомных частиц! А это значит:
• Нужно, чтобы именно такие частицы
• сложились именно в такой конфигурации
• с одинаковыми связями между ними
• у двух разных макроскопических систем.
Изучим, что для этого потребовалось бы.

Одна молекула воды – это один атом кислорода и два атома водорода, связанные вместе. Когда молекулы замерзшей воды связываются вместе, с каждой из них оказываются связанными четыре других молекулы: одна в каждой из вершин тетраэдра с центром этой молекуле. В результате молекулы воды упаковываются в решётку – шестиугольную кристаллическую решётку. Но большие призматические «кубики» льда, такие, какие можно наблюдать у отложений кварца, встречаются крайне редко. Переходя с малейших масштабов и конфигураций на верхний уровень, вы увидите, что верхняя и нижняя поверхности этой решётки очень плотно упакованы и связаны друг с другом – с двух сторон оказываются плоские грани. И наоборот, на оставшихся гранях видны отдельные молекулы, и новые молекулы воды связываются с ними в более произвольном порядке. На углах шестиугольника связи получаются самые слабые, поэтому в растущих кристаллах и появляется шестиугольная симметрия.

Формирование и рост снежного кристалла, фрагмент видео
Затем новообразованные структуры вырастают уже по этой симметричной схеме, поддерживая шестиугольную асимметрию при достижении определённого размера. У больших и сложных снежных кристаллов через микроскоп можно найти сотни видимых черт. Можно видеть сотни отличительных черт, и порядка 1019 молекул воды, составляющих типичную снежинку, если верить Чарльзу Найту из Национального центра атмосферных исследований. И для каждой из этих особенностей существуют миллионы подходящих мест, в которых могут сформироваться новые отростки. Так сколько из этих новых особенностей может сформировать снежинка, и при этом оказаться идентичной с какой-то другой?
Полное видео
Каждый год на землю выпадает порядка 3*1013 кубических метров снега, а в каждом кубическом метре содержится примерно 3*1010 снежинок. Поскольку Земля существует порядка 4,5 млрд лет, за всю её историю на неё упало порядка 1034 снежинок. С точки зрения статистики количество отдельных уникальных симметрически ветвящихся особенностей снежинки, которое она могла бы себе позволить, чтобы на протяжении всей истории Земли у неё появился идентичный близнец, равно пяти. При этом у реальных, полностью выросших естественных снежинок таких особенностей сотни.

Даже на миллиметровом масштабе на снежинке можно рассмотреть множество несовершенств, затрудняющих воспроизводство другой, точно такой же снежинки
Две идентичные снежинки реально будет найти, только если рассматривать самые маленькие кристаллы на начальных стадиях роста. А если спуститься на молекулярный уровень, ситуация становится ещё хуже. Обычно у кислорода есть 8 протонов и 8 нейтронов, а у водорода – 1 протон и 0 нейтронов. Однако примерно в одном из 500 атомов кислорода присутствует 10 нейтронов, а в одном из 5000 атомов водорода есть 1 нейтрон, а не 0. С такими цифрами, если даже вы создадите идеальный шестиугольный снежный кристалл, и доберётесь до количества кристаллов, выпавших на землю за всю историю — 1034, вам нужно будет всего лишь дорасти до размера в несколько тысяч молекул, то есть, до снежинки размером в 0,01 микрон (это меньше длины волны видимого света), чтобы получить уникальную структуру, которой мир ещё не видал.

При изучении шестиугольного снежного кристалла с ободком под электронным микроскопом видно, сколько у него есть тонких и разнообразных несовершенств, которые невозможно воспроизвести на молекулярном уровне
Но если вы хотите игнорировать различия на атомном и молекулярном уровне, и использовать искусственные снежинки, у вас есть шанс. Исследователь снежинок Кеннет Либбрехт из Калтеха разработал технологию создания искусственных идентичных снежинок и их фотографирования при помощи особого микроскопа, который он назвал SnowMaster 9000.
Выращивая снежинки рядом в определённых лабораторных условиях он показал, что можно создать две снежинки, неотличимые друг от друга.

Ну или типа того. Они неотличимы для человека, смотрящего в микроскоп – но на самом деле они отличаются. Как и у однояйцевых близнецов, у них есть множество отличий: разные места связей молекул, немного разные ветвления, и чем они больше, тем лучше видны эти отличия. Именно поэтому эти снежинки делают небольшими, а микроскоп взят мощный: чем проще снежинки, тем меньше между ними различий.

Тем не менее, множество снежинок похожи друг на друга. Но если искать на самом деле идентичные снежинки, на структурном, молекулярном или атомном уровне, то природа вам этого никогда не даст. Количество возможностей слишком велико не только для истории Земли, но и для истории Вселенной. Если подсчитать, сколько планет Земля нам потребуется для того, чтобы у нас был шанс найти две одинаковых снежинки за все 13,8 млрд лет существования Вселенной, то получится число порядка 1010 000 000 000 000 000 000. А поскольку в наблюдаемой Вселенной есть всего 1080 атомов, это очень маловероятно. Так что, судя по всему, все снежинки действительно уникальны.
Итан Сигель – астрофизик, популяризатор науки, автор блога Starts With A Bang! Написал книги «За пределами галактики» [Beyond The Galaxy], и «Трекнология: наука Звёздного пути» [Treknology].
Комментарии (22)

Gummilion
28.09.2017 02:10+9Ну если на микроуровне, то и двух одинаковых гаек не бывает — какими-то микроцарапинами и внутренними дефектами они будут отличаться, даже если на самом высокоточном станке их делать.

betrachtung
28.09.2017 06:12Как тут не вспомнить Эллиса?
Мне кажется, много снежинок одинаковых… и много одинаковых людей.

SinsI
28.09.2017 09:33Что если их делать искусственно, при температурах около абсолютного нуля, в вакууме?
Metallikus
28.09.2017 14:24+1Тогда они сферические получаются. :-) Кристаллическая решётка не может образоваться при слишком резком охлаждении.

DrZlodberg
28.09.2017 09:41+4А всё-таки, почему они симметричные? Ладно, конфигурация молекул вблизи даёт 6-угольник. Но что заставляет их оставаться симметричными на относительно больших расстояниях (на концах лучей, например)? Или начальная конфигурация первых нескольких молекул жестко задаёт весь дальнейший рост кристалла? Типа клеточного автомата. Тогда возникает вопрос — а нельзя ли написать симулятор роста снежинки, который генерил бы их по начальным условиям?

Stirliz85
28.09.2017 11:39Полагаю, что какие-то особенности внешней среды обуславливают форму кристализуемой снежинки. Влажность, температура, давление, еще что-нибудь. В рамках одной снежинки эти параметры не сильно меняются, а у двух соседних снежинок уже солидный такой разброс.
Если кто-то знает точно, то пусть поправит.
vconst
28.09.2017 11:53+2Таки да — самого главного и интересного в стой статье нет.
Есть два основных параметра — которые влияют на направление роста кристаллов: влажность и температура, при одном сочетании (я точно не вспомню каком именно — но это не так важно в данном случае) кристалл растет в длину, при другом — в ширину. И да, если снежинка достаточно маленькая, то эти параметры меняются для нее не сильно и попеременный рост в длину и в ширь — происходит одинаково на всей снежинке, а для разных снежинок — эти параметры уже не совпадают, потому что между ними достаточно большое расстояние.
Потому, если в лабораторных условиях обеспечить очень точные параметры влажности и температуры в большом объеме, а затем умудриться менять их синхронно для всего объема, не допуская сильных флуктуаций в отдельных участках — то будут получаться максимально похожие снежинки, практически близнецы — неотличимые на оптическом уровне. Такие эксперименты ставили и они были успешны.

SpiridonovAA
28.09.2017 10:35+1Вообще-то может. Вероятность этого крайне маленькая, стремящаяся к нулю, но она не нулевая
andrey_aksamentov
28.09.2017 13:43-1В идентичной параллельной вселенной возможно.
andrey_aksamentov
28.09.2017 13:49Сама снежинка уже не идентична себе по определению. Ведь постоянно изменяется ее молекулярная структура относительно времени и гравитации.

Tyusha
28.09.2017 20:26Как-то путанно у Итана. Вот тут вообще не поняла:
А если спуститься на молекулярный уровень, ситуация становится ещё хуже. Обычно у кислорода есть 8 протонов и 8 нейтронов, а у водорода – 1 протон и 0 нейтронов. Однако примерно в одном из 500 атомов кислорода присутствует 10 нейтронов, а в одном из 5000 атомов водорода есть 1 нейтрон, а не 0. С такими цифрами, если даже вы создадите идеальный шестиугольный снежный кристалл, и доберётесь до количества кристаллов, выпавших на землю за всю историю — 10^34, вам нужно будет всего лишь дорасти до размера в несколько тысяч молекул, то есть, до снежинки размером в 0,01 микрон (это меньше длины волны видимого света), чтобы получить уникальную структуру, которой мир ещё не видал.
1. Молекулярный уровень или ядерный?
2. Причём здесь изотопический состав воды, он же на химию он не влияет. Или в данном случае это оказывается существенным?
3. А потом такое предложение… Несколько раз прочитала, до сих пор не въехала.
Согласно моим, скорее всего неправильным, представлениям сначала образуется асимметричный зародыш, который полностью определяет будущий узор снежинки. С некоторого масштаба возникает некий «дальний порядок», который затем сменяется фрактальным ростом. Причём конфигурация уже полностью предопределёна зародышем и дислокациями в нём. Поэтому вопрос сводится к размеру неструктурированных зародышей и числу комбинаций для таких суб-снежиночных структур, а не самих уже выросших снежинок.
Ещё раз повторюсь, это мои умозаключения. Буду рада квалифицированному комментарию. У Итана не получилось.ClearAirTurbulence
29.09.2017 16:221. Логика такая: если молекулы состоят из разных атомов, то они тоже разные.
2. На химию не влияет. Но на физическом уровне отличающиеся атомы могут формировать отличные структуры. Существенным является только с точки зрения выбранных критериев одинаковости снежинок.
3. Идея последнего предложения такова:
— Примем, что у нас есть 10^34 снежинок (выпавших на Землю за время ее существования)
— Примем, что все снежинки — идеально шестиугольны (что на самом деле не так)
— При этих допущениях, при достижении снежинками диаметра 0.01 микрон количество атомов станет достаточно большим, чтобы среди них (по статистике) попались «нестандартные», и как следствие, начиная с этого размера, все снежинки различаются.
На всякий случай, оригинал. Переведено неп
At this rate, even if you had a perfectly hexagonal snow crystal, and you made approximately 10?? snow crystals over the history of planet Earth, you’d only need to reach a size of a few thousand molecules, or a snowflake just 0.01 microns across (smaller than the wavelength of visible light) to arrive at a unique structure that the planet had never seen before.


maxzhurkin
Наверняка же есть некий аналог парадокса дней рождения для снежинок?
TheShock
А это значит, что есть порядка 10342=1068 пар снежинок. (что очень сильно больше, хотя и выглядит похоже)
А в этом предложении:
Он ищет не «две одинаковые снежинки», а «вероятность того, что есть еще одна такая же снежинка, как выбранная». Следовательно, если искать две любых одинаковых снежинки, а не снежинку, которая похожа на данную, то вероятность очень сильно выростает.
Но, возможно, это нюансы перевода и он считал именно для всех пар?