Привет, Хабр! Продолжаем серию материалов от выпускника нашей программы Deep Learning, Кирилла Данилюка, об использовании сверточных нейронных сетей для распознавания образов — CNN (Convolutional Neural Networks).
В прошлом посте мы начали разговор о подготовке данных для обучения сверточной сети. Сейчас же настало время использовать полученные данные и попробовать построить на них нейросетевой классификатор дорожных знаков. Именно этим мы и займемся в этой статье, добавив дополнительно к сети-классификатору любопытный модуль — STN. Датасет мы используем тот же, что и раньше.
Spatial Transformer Network (STN) — один из примеров дифференцируемых LEGO-модулей, на основе которых можно строить и улучшать свою нейросеть. STN, применяя обучаемое аффинное преобразование с последующей интерполяцией, лишает изображения пространственной инвариантности. Грубо говоря, задача STN состоит в том, чтобы так повернуть или уменьшить-увеличить исходное изображение, чтобы основная сеть-классификатор смогла проще определить нужный объект. Блок STN может быть помещен в сверточную нейронную сеть (CNN), работая в ней по большей части самостоятельно, обучаясь на градиентах, приходящих от основной сети.
Весь исходный код проекта доступен на GitHub по ссылке. Оригинал этой статьи можно посмотреть на Medium.
Чтобы иметь базовое представление о работе STN, взгляните на 2 примера ниже:
 Слева: исходное изображение. Справа: то же изображение, преобразованное STN. Spatial transformers распознают наиболее важную часть изображения и затем масштабируют или вращают его, чтобы сфокусироваться на этой части.
Слева: исходное изображение. Справа: то же изображение, преобразованное STN. Spatial transformers распознают наиболее важную часть изображения и затем масштабируют или вращают его, чтобы сфокусироваться на этой части.
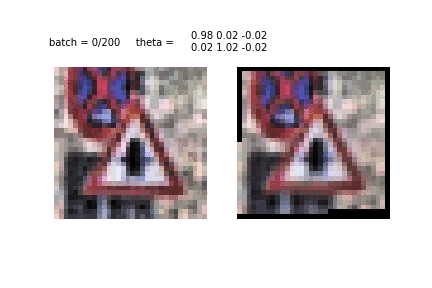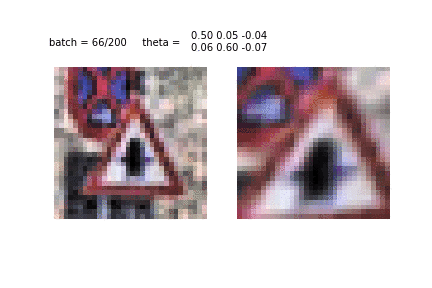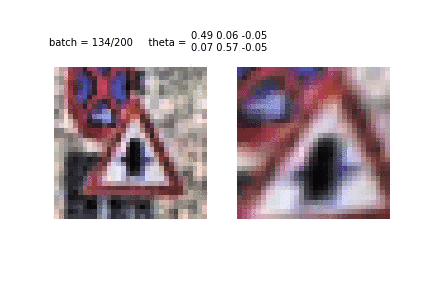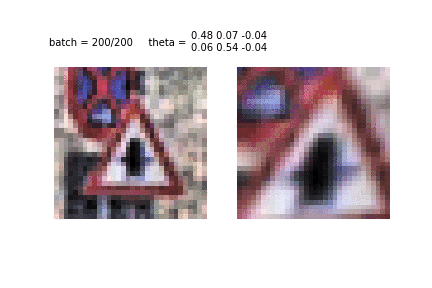 Еще один пример обучения STN и преобразования изображений. Это первая эпоха и первые десятки батчей, использованных для обучения. Видно, как STN распознает очертания знака, чтобы затем сконцентрироваться на нем самом.
Еще один пример обучения STN и преобразования изображений. Это первая эпоха и первые десятки батчей, использованных для обучения. Видно, как STN распознает очертания знака, чтобы затем сконцентрироваться на нем самом.
STN работает даже в сложных случаях (например, 2 знака на изображении), но самое главное — STN действительно улучшает качество классификатора (IDSIA в моем случае).
Одна из проблем сверточных нейронных сетей — слишком низкая инвариантность к входным данным: разный масштаб, точка съемки, шум на заднем плане и многое другое. Можно, конечно, сказать, что операция пулинга, так не любимая Хинтоном, дает некоторую инвариантность, но фактически она просто уменьшает размер feature map, что выливается в потерю информации.
К сожалению, из-за маленького рецептивного поля в стандартном 2х2 пулинге пространственная инвариантность может быть достигнута лишь в глубоких слоях, близких к output-слою. Также пулинг не обеспечивает инвариантность вращения и масштаба. Кевин Закка хорошо объяснил причину этого в своем посте.
Основной и самый распространенный способ сделать модель устойчивой к этим вариациям — аугментация датасета, что мы и сделали в предыдущей статье:

Аугментированные изображения. В этом посте мы не будем использовать аугментацию.
В таком подходе нет ничего плохого, но нам бы хотелось разработать более умный и автоматизированный метод предобработки изображений, который должен способствовать увеличению точности классификатора. Spatial transformer network (STN) — как раз то, что нам нужно.
Ниже еще один пример работы STN:
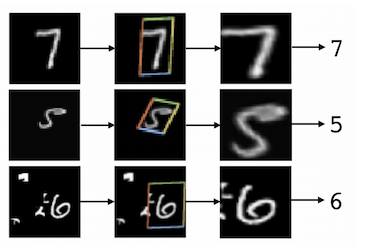
Пример из датасета MNIST из статьи-первоисточника. Cluttered MNIST (слева), целевой объект, распознанный STN (центр), преобразованное изображение (справа).
Работа STN модуля может быть сведена к следующему процессу (не включая обучение):
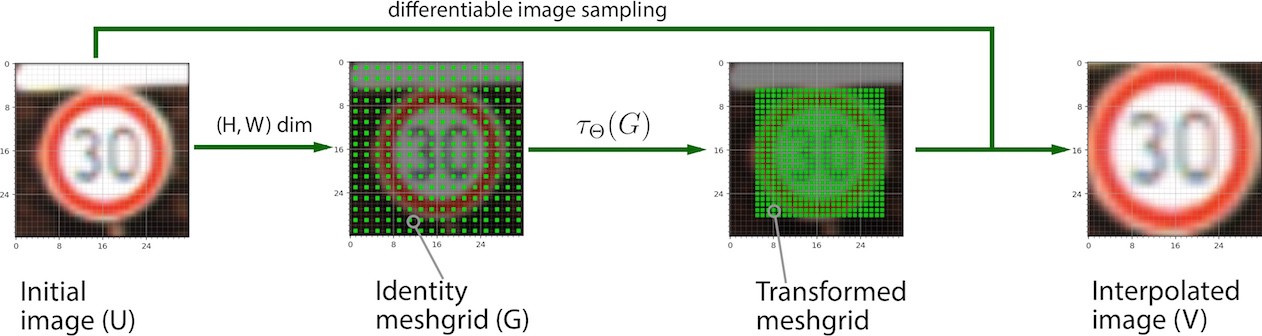
Применение STN преобразования в 4 шага при известной матрице линейных преобразований ?.
Теперь рассмотрим подробнее этот процесс и каждый его этап.
Шаг 1. Определить матрицу преобразований ?, которая описывает саму трансформацию:
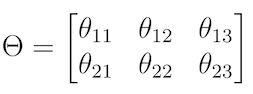
Аффинное преобразование матрицы ?.
При этом каждому преобразованию соответствует своя матрица. Нас интересуют следующие 4:
Шаг 2. Вместо того, чтобы применять преобразование напрямую к исходному изображению (U), создадим выборочную сетку (sampling meshgrid) того же размера, что и U. Выборочная сетка — это набор индексов (x_t, y_t), которые покрывают исходное пространство изображений. Сетка не содержит в себе никакой информации о цвете изображений. Лучше это объясняется в коде ниже:
Поскольку это фактическая имплементация в TensorFlow, чтобы понять общую идею, переведем этот код в аналог на numpy:
Шаг 3. Применить матрицу линейных преобразований к созданной выборочной сетке, чтобы получить новый набор точек на сетке, каждая из которых может быть определена как результат умножения матрицы ? на вектор координат (x_t, y_t) со свободным членом:
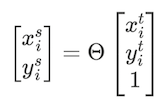
Шаг 4. Получить подвыборку V, используя исходную карту признаков, преобразованную выборочную сетку (см. Шаг 3) и дифференцируемую функцию интерполяции на ваш выбор (например, билинейная). Интерполяция необходима, так как нам нужно перевести результат сэмплинга (потенциально возможные дробные значения пикселей) в целые числа.
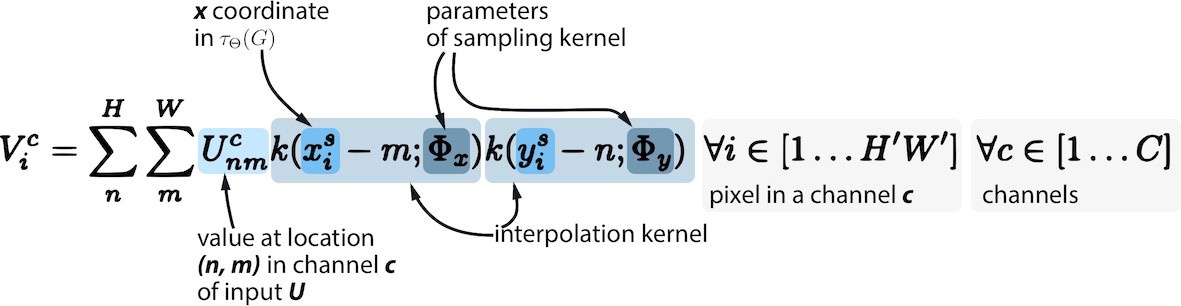
Сэмплинг и интерполяция
Задача обучения. Говоря в общем, если бы мы заранее знали нужные нам значения ? для каждого исходного изображения, можно было бы начинать описанный выше процесс. На деле же, нам бы хотелось извлекать ? из данных с помощью машинного обучения. Это сделать вполне реально. Во-первых, нам нужно убедиться, что функция потерь классификатора дорожных знаков может быть минимизирована с помощью backprop через сэмплер. Во-вторых, мы находим градиенты по U и G (meshgrid): именно поэтому функция интерполяции должна быть дифференцируема или, хотя бы, частично дифференцируема. В-третьих, рассчитываем частные производные x и y по ?. Технические выкладки можно прочитать в исходной пейпе.
Наконец, мы создаем LocNet (локализующая сеть-регрессор), единственной задачей которой будет обучиться и спрогнозировать корректные ? для принимаемого на вход изображения, используя функцию потерь, которая была минимизирована через общий backprop.
Главное достоинство такого подхода заключается в том, что мы получаем дифференцируемый автономный модуль с памятью (в виде обучаемых весов), который может быть помещен в любую часть CNN.

Заметьте, как меняется ?, пока STN обучается распознавать целевой объект (дорожный знак) на изображениях.
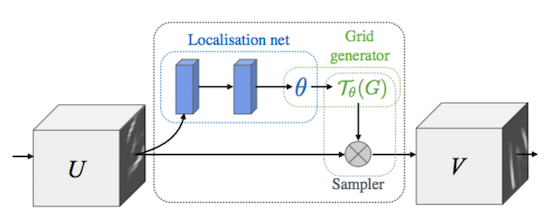
Ниже представлена схема работы STN из оригинальной статьи:
Мы рассмотрели все этапы построения STN: создание LocNet, генератора выборочной сетки (meshgrid) и сэмплера. Теперь построим и обучим на TensorFlow весь классификатор, который включает в свой граф и STN.
Весь код модели, конечно, не уместится в рамки одной статьи, но он доступен в виде Jupyter-ноутбука в репозитории на GitHub.
В этой же статье я акцентирую внимание на некоторых важных частях кода и этапах обучения модели.
Во-первых, наша конечная цель — научиться распознавать дорожные знаки, и для ее достижения нам нужно создать какой-то классификатор и обучить его. Вариантов у нас много: от LeNet и до любой другой SOTA-нейросети. В процессе работы над проектом, вдохновившись работой Moodstocks по STN (реализованной в Torch), я использовал архитектуру нейронной сети IDSIA, хотя ничто не мешало взять что-то другое.
На втором этапе нам нужно определить и обучить STN модуль, который, принимая на вход исходное изображение, преобразует его с помощью сэмплера и на выходе получается новое изображение (или минибатч, если мы работаем в батч-режиме), которое в свою очередь используется классификатором.
Отмечу, что STN можно легко убрать из графа вычислений, заменив весь модуль простым генератором батчей. В таком случае, мы просто получим обычную сеть-классификатор.
Вот общая схема работы полученной двойной нейронной сети:
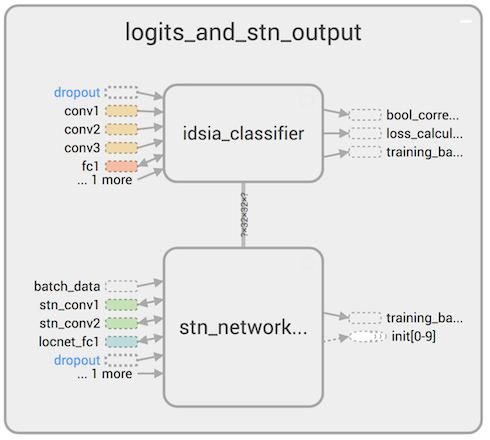
STN преобразует исходные изображения и подает их на вход IDSIA, которая обучается с помощью backprop и затем классифицирует дорожные знаки.
Ниже приведена часть DAG, в рамках которого исходные изображения преобразуются с помощью STN и подаются на вход классификатору (IDSIA), который рассчитывает логиты:
Теперь, когда мы знаем метод расчета логитов (STN + IDSIA network), следующим шагом будет оптимизация функции потерь ( в качестве которой мы будем использовать кросс-энтропию или log loss — стандартный выбор для решения задачи классификации):
Затем нам нужно задать операции (ops) оптимизации и обучения, которые должны распространять ошибки обратно к входным слоям:
Я инициализировал сеть с большим значением learning rate (0.02), чтобы градиенты могли быстрее распространять информацию к LocNet STN, которая расположена во внешних слоях всей нейронной сети. В противном случае эта сеть будет обучаться медленнее (из-за проблемы «исчезающего» градиента). Маленькие исходные значения learning rate не позволяют нейросети хорошо приближать мелкие дорожные знаки на изображении.
Часть DAG, которая рассчитывает логиты (выход сети) добавляется в граф довольно просто:
Кусок кода выше развертывает всю сеть — STN + IDSIA, их мы обсудим подробнее ниже.
Вдохновленный работой Moodstocks и оригинальной статьей от IDSIA Swiss AI Group, в которой они использовали ансамбль из CNN, чтобы улучшить ранее достигнутое качество модели, я взял общую идею архитектуры одной сети из ансамбля и реализовал его в TensorFlow самостоятельно. Получившаяся структура классификатора выглядит следующим образом:
Все это проиллюстрировано ниже:
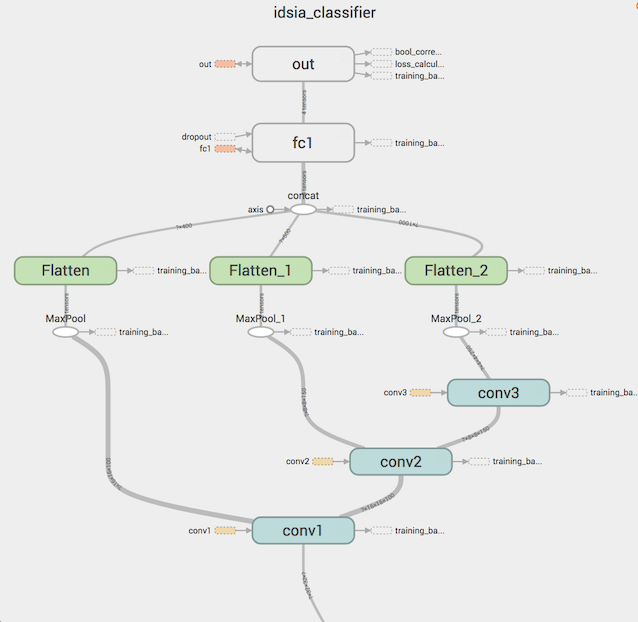
Как видно, результаты функций активации каждого сверточного слоя объединяются в один вектор, который уже и подается полносвязным слоям. Это пример multiscale-фич, которые дополнительно улучшают качество классификатора.
На вход conv1 подается преобразованное STN изображение, как мы и обсуждали ранее.
Среди всего разнообразия моделей TensorFlow можно найти реализацию STN, которая и будет использована в нашей сети.
Наша задача — обозначить и обучить LocNet, обеспечить transformer корректными значениями ? и вставить STN модуль в DAG Tensorflow. transformer генерирует сетку и обеспечивает преобразования и интерполяцию.
Конфигурация LocNet представлена ниже:
Сверточные слои LocNet:
Fully-connected часть LocNet:
Структура сверточных слоев LocNet похожа на IDSIA (хотя LocNet состоит из 2 слоев вместо 3, и в ней мы сначала делаем пуллинг). Более любопытна структура полносвязных слоев:
Проблема использования STN модуля с CNN заключается в необходимости следить за тем, чтобы обе сети не переобучались, что делает процесс обучения сложным и нестабильным. С другой стороны, добавление небольшого количества аугментированных данных (особенно аугментирование яркости) в обучающую выборку позволяет сетям не переобучаться. В любом случае, преимущества перевешивают недостатки: даже без аугментации мы получаем хорошие результаты, а STN+IDSIA превосходят по точности IDSIA без этого модуля на 0,5-1%.
В процессе обучения были использованы следующие параметры:
Уже после 10 эпох мы получаем точность равную 99,3% на validation наборе данных. CNN все еще переобучается, но не забывайте, что мы используем двойную сложную сетку на исходном датасете без его расширения аугментациями. По правде говоря, добавив аугментацию, мне удалось получить точность равную 99,6% на validation сете после 10 итераций (хотя значительно увеличилось время обучения).
Ниже приведены результаты обучения моделей (idsia_1 — это IDSIA сеть без модуля, idsia_stn — это STN+IDSIA). Это точность всей сети на валидации.
STN+IDSIA показывает себя лучше, чем IDSIA сеть без модуля, хотя, обучается она дольше. Отмечу, что точность на графике выше рассчитана по батчам, а не по всей валидации.
Наконец, вот результат работы STN трансформера после обучения:

Что ж, резюмируем:

В прошлом посте мы начали разговор о подготовке данных для обучения сверточной сети. Сейчас же настало время использовать полученные данные и попробовать построить на них нейросетевой классификатор дорожных знаков. Именно этим мы и займемся в этой статье, добавив дополнительно к сети-классификатору любопытный модуль — STN. Датасет мы используем тот же, что и раньше.
Spatial Transformer Network (STN) — один из примеров дифференцируемых LEGO-модулей, на основе которых можно строить и улучшать свою нейросеть. STN, применяя обучаемое аффинное преобразование с последующей интерполяцией, лишает изображения пространственной инвариантности. Грубо говоря, задача STN состоит в том, чтобы так повернуть или уменьшить-увеличить исходное изображение, чтобы основная сеть-классификатор смогла проще определить нужный объект. Блок STN может быть помещен в сверточную нейронную сеть (CNN), работая в ней по большей части самостоятельно, обучаясь на градиентах, приходящих от основной сети.
Весь исходный код проекта доступен на GitHub по ссылке. Оригинал этой статьи можно посмотреть на Medium.
Чтобы иметь базовое представление о работе STN, взгляните на 2 примера ниже:

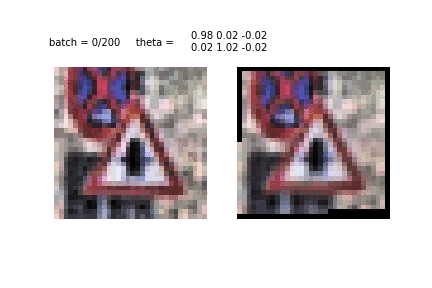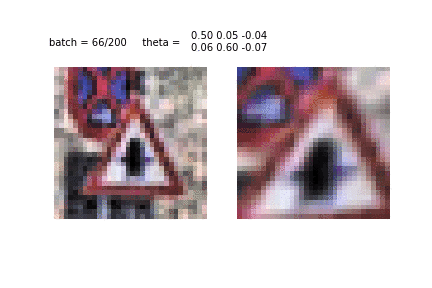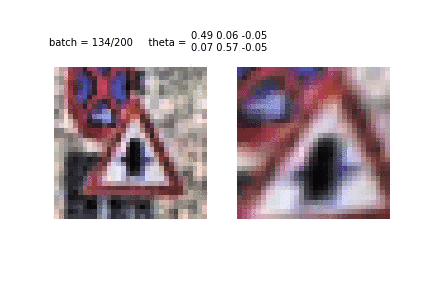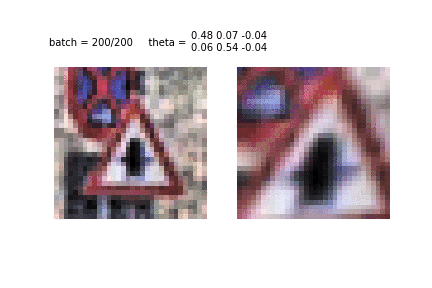
STN работает даже в сложных случаях (например, 2 знака на изображении), но самое главное — STN действительно улучшает качество классификатора (IDSIA в моем случае).
Общее устройство STN: курс молодого бойца
Одна из проблем сверточных нейронных сетей — слишком низкая инвариантность к входным данным: разный масштаб, точка съемки, шум на заднем плане и многое другое. Можно, конечно, сказать, что операция пулинга, так не любимая Хинтоном, дает некоторую инвариантность, но фактически она просто уменьшает размер feature map, что выливается в потерю информации.
К сожалению, из-за маленького рецептивного поля в стандартном 2х2 пулинге пространственная инвариантность может быть достигнута лишь в глубоких слоях, близких к output-слою. Также пулинг не обеспечивает инвариантность вращения и масштаба. Кевин Закка хорошо объяснил причину этого в своем посте.
Основной и самый распространенный способ сделать модель устойчивой к этим вариациям — аугментация датасета, что мы и сделали в предыдущей статье:

Аугментированные изображения. В этом посте мы не будем использовать аугментацию.
В таком подходе нет ничего плохого, но нам бы хотелось разработать более умный и автоматизированный метод предобработки изображений, который должен способствовать увеличению точности классификатора. Spatial transformer network (STN) — как раз то, что нам нужно.
Ниже еще один пример работы STN:

Пример из датасета MNIST из статьи-первоисточника. Cluttered MNIST (слева), целевой объект, распознанный STN (центр), преобразованное изображение (справа).
Работа STN модуля может быть сведена к следующему процессу (не включая обучение):

Применение STN преобразования в 4 шага при известной матрице линейных преобразований ?.
Теперь рассмотрим подробнее этот процесс и каждый его этап.
STN: этапы преобразования
Шаг 1. Определить матрицу преобразований ?, которая описывает саму трансформацию:
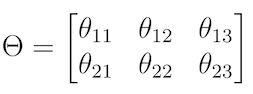
Аффинное преобразование матрицы ?.
При этом каждому преобразованию соответствует своя матрица. Нас интересуют следующие 4:
- Тождественное преобразование(на выходе то же самое изображение). Это наши исходные значения ?. В данном случае, матрица ? диагональная:
theta = np.array([[1.0, 0, 0], [0, 1.0, 0]]) - Вращение (против часовой стрелки, 45?). cos(45?) = 1/sqrt(2) ? 0.7:
theta = np.array([[0.7, -0.7, 0], [0.7, 0.7, 0]]) - Приближение. Приближение к центру (в 2 раза):
theta = np.array([[0.5, 0, 0], [0, 0.5, 0]]) - Отдаление. Отдаление от центра (в 2 раза):
theta = np.array([[2.0, 0, 0], [0, 2.0, 0]])
Шаг 2. Вместо того, чтобы применять преобразование напрямую к исходному изображению (U), создадим выборочную сетку (sampling meshgrid) того же размера, что и U. Выборочная сетка — это набор индексов (x_t, y_t), которые покрывают исходное пространство изображений. Сетка не содержит в себе никакой информации о цвете изображений. Лучше это объясняется в коде ниже:
# Implemented in https://github.com/tensorflow/models/blob/master/transformer/spatial_transformer.py
# As I mentioned, we only need height and width of the original image
def _meshgrid(height, width):
with tf.variable_scope('_meshgrid'):
x_t = tf.matmul(tf.ones(shape=tf.stack([height, 1])),
tf.transpose(tf.expand_dims(tf.linspace(-1.0, 1.0, width), 1), [1, 0]))
y_t = tf.matmul(tf.expand_dims(tf.linspace(-1.0, 1.0, height), 1),
tf.ones(shape=tf.stack([1, width])))
x_t_flat = tf.reshape(x_t, (1, -1))
y_t_flat = tf.reshape(y_t, (1, -1))
ones = tf.ones_like(x_t_flat)
grid = tf.concat(axis=0, values=[x_t_flat, y_t_flat, ones])
return gridПоскольку это фактическая имплементация в TensorFlow, чтобы понять общую идею, переведем этот код в аналог на numpy:
x_t, y_t = np.meshgrid(np.linspace(-1, 1, width), np.linspace(-1, 1, height))Шаг 3. Применить матрицу линейных преобразований к созданной выборочной сетке, чтобы получить новый набор точек на сетке, каждая из которых может быть определена как результат умножения матрицы ? на вектор координат (x_t, y_t) со свободным членом:
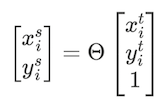
Шаг 4. Получить подвыборку V, используя исходную карту признаков, преобразованную выборочную сетку (см. Шаг 3) и дифференцируемую функцию интерполяции на ваш выбор (например, билинейная). Интерполяция необходима, так как нам нужно перевести результат сэмплинга (потенциально возможные дробные значения пикселей) в целые числа.

Сэмплинг и интерполяция
Задача обучения. Говоря в общем, если бы мы заранее знали нужные нам значения ? для каждого исходного изображения, можно было бы начинать описанный выше процесс. На деле же, нам бы хотелось извлекать ? из данных с помощью машинного обучения. Это сделать вполне реально. Во-первых, нам нужно убедиться, что функция потерь классификатора дорожных знаков может быть минимизирована с помощью backprop через сэмплер. Во-вторых, мы находим градиенты по U и G (meshgrid): именно поэтому функция интерполяции должна быть дифференцируема или, хотя бы, частично дифференцируема. В-третьих, рассчитываем частные производные x и y по ?. Технические выкладки можно прочитать в исходной пейпе.
Наконец, мы создаем LocNet (локализующая сеть-регрессор), единственной задачей которой будет обучиться и спрогнозировать корректные ? для принимаемого на вход изображения, используя функцию потерь, которая была минимизирована через общий backprop.
Главное достоинство такого подхода заключается в том, что мы получаем дифференцируемый автономный модуль с памятью (в виде обучаемых весов), который может быть помещен в любую часть CNN.

Заметьте, как меняется ?, пока STN обучается распознавать целевой объект (дорожный знак) на изображениях.
Ниже представлена схема работы STN из оригинальной статьи:

Мы рассмотрели все этапы построения STN: создание LocNet, генератора выборочной сетки (meshgrid) и сэмплера. Теперь построим и обучим на TensorFlow весь классификатор, который включает в свой граф и STN.
Построение модели в TensorFlow
Весь код модели, конечно, не уместится в рамки одной статьи, но он доступен в виде Jupyter-ноутбука в репозитории на GitHub.
В этой же статье я акцентирую внимание на некоторых важных частях кода и этапах обучения модели.
Во-первых, наша конечная цель — научиться распознавать дорожные знаки, и для ее достижения нам нужно создать какой-то классификатор и обучить его. Вариантов у нас много: от LeNet и до любой другой SOTA-нейросети. В процессе работы над проектом, вдохновившись работой Moodstocks по STN (реализованной в Torch), я использовал архитектуру нейронной сети IDSIA, хотя ничто не мешало взять что-то другое.
На втором этапе нам нужно определить и обучить STN модуль, который, принимая на вход исходное изображение, преобразует его с помощью сэмплера и на выходе получается новое изображение (или минибатч, если мы работаем в батч-режиме), которое в свою очередь используется классификатором.
Отмечу, что STN можно легко убрать из графа вычислений, заменив весь модуль простым генератором батчей. В таком случае, мы просто получим обычную сеть-классификатор.
Вот общая схема работы полученной двойной нейронной сети:

STN преобразует исходные изображения и подает их на вход IDSIA, которая обучается с помощью backprop и затем классифицирует дорожные знаки.
Ниже приведена часть DAG, в рамках которого исходные изображения преобразуются с помощью STN и подаются на вход классификатору (IDSIA), который рассчитывает логиты:
def stn_idsia_inference_type2(batch_x):
with tf.name_scope('stn_network_t2'):
# Unrolling the STN's LocNet -- stn_output is theta-matrix
stn_output = stn_LocNet_type2(stn_convolve_pool_flatten_type2(batch_x))
# Grid generator and sampler
transformed_batch_x = transformer(batch_x, stn_output, (32,32, TF_CONFIG['channels']))
with tf.name_scope('idsia_classifier'):
# IDSIA uses transformed_batch_x from STN. Here we unroll the conv layers of IDSIA
features, batch_act = idsia_convolve_pool_flatten(transformed_batch_x, multiscale=True)
# Unrolling FC layers of IDSIA
logits = idsia_fc_logits(features, multiscale=True)
# Returning lots of objects. `logits` is the one that is really required for the model
return logits, transformed_batch_x, batch_actТеперь, когда мы знаем метод расчета логитов (STN + IDSIA network), следующим шагом будет оптимизация функции потерь ( в качестве которой мы будем использовать кросс-энтропию или log loss — стандартный выбор для решения задачи классификации):
def calculate_loss(logits, one_hot_y):
with tf.name_scope('Predictions'):
predictions = tf.nn.softmax(logits)
with tf.name_scope('Model'):
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=one_hot_y)
with tf.name_scope('Loss'):
loss_operation = tf.reduce_mean(cross_entropy)
return loss_operationЗатем нам нужно задать операции (ops) оптимизации и обучения, которые должны распространять ошибки обратно к входным слоям:
boundaries = [100, 250, 500, 1000, 8000]
values = [0.02, 0.01, 0.005, 0.003, 0.001, 0.0001]
starter_learning_rate = 0.02
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.piecewise_constant(global_step, boundaries, values)
with tf.name_scope('accuracy'):
accuracy_operation = tf.reduce_mean(casted_corr_pred)
with tf.name_scope('loss_calculation'):
loss_operation = calculate_loss(logits, one_hot_y)
with tf.name_scope('adam_optimizer'):
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
with tf.name_scope('training_backprop_operation'):
training_operation = optimizer.minimize(loss_operation, global_step=global_step)Я инициализировал сеть с большим значением learning rate (0.02), чтобы градиенты могли быстрее распространять информацию к LocNet STN, которая расположена во внешних слоях всей нейронной сети. В противном случае эта сеть будет обучаться медленнее (из-за проблемы «исчезающего» градиента). Маленькие исходные значения learning rate не позволяют нейросети хорошо приближать мелкие дорожные знаки на изображении.
Часть DAG, которая рассчитывает логиты (выход сети) добавляется в граф довольно просто:
with tf.name_scope('batch_data'):
x = tf.placeholder(tf.float32, (None, 32, 32, TF_CONFIG['channels']), name="InputData")
y = tf.placeholder(tf.int32, (None), name="InputLabels")
one_hot_y = tf.one_hot(y, n_classes, name='InputLabelsOneHot')
#### INIT
with tf.name_scope('logits_and_stn_output'):
logits, stn_output, batch_act = stn_idsia_inference_type2(x)Кусок кода выше развертывает всю сеть — STN + IDSIA, их мы обсудим подробнее ниже.
IDSIA: сеть-классификатор
Вдохновленный работой Moodstocks и оригинальной статьей от IDSIA Swiss AI Group, в которой они использовали ансамбль из CNN, чтобы улучшить ранее достигнутое качество модели, я взял общую идею архитектуры одной сети из ансамбля и реализовал его в TensorFlow самостоятельно. Получившаяся структура классификатора выглядит следующим образом:
- Слой 1: Convolutional (batch normalization, relu, dropout). Kernel : 7x7, 100 фильтров. На вход: 32x32x1 (В наборе из 256). На выходе: 32x32x100.
- Слой 2: Max Pooling. На вход: 32x32x100. На выходе: 16x16x100.
- Слой 3: Convolutional (batch normalization, relu, dropout). Kernel : 5x5, 150 фильтров. На вход: 16x16x100 (in a batch of 256). На выходе: 16x16x150.
- Слой 4: Max Pooling. На вход: 16x16x150. На выходе: 8x8x150.
- Слой 5: Convolutional (batch normalization, relu, dropout). Kernel : 5x5, 250 фильтров. На вход: 16x16x100 (в наборе из 256). На выходе: 16x16x150.
- Слой 6: Max Pooling. На вход: 8x8x250. На выходе: 4x4x250.
- Слой 7: Дополнительный pooling для multiscale-фич. Kernels: 8, 4, 2 для слоев 1, 2 и 3 соответственно.
- Слой 8: Вытягивание и конкатенация фич в вектор multiscale-фич. На входе: 2x2x100; 2x2x150; 2x2x250. На выходе: вектор фичей 400+600+1000 = 2000 для полносвязных слоев
- Слой 9: Fully-connected (batch normalization, relu, dropout). На входе: 2000 признаков (в наборе из 256). 300 нейронов.
- Слой 10: Logits (batch normalization). На входе: 300 признаков. На выходе: логиты (43 класса).
Все это проиллюстрировано ниже:

Как видно, результаты функций активации каждого сверточного слоя объединяются в один вектор, который уже и подается полносвязным слоям. Это пример multiscale-фич, которые дополнительно улучшают качество классификатора.
На вход conv1 подается преобразованное STN изображение, как мы и обсуждали ранее.
Spatial Transformers в TensorFlow
Среди всего разнообразия моделей TensorFlow можно найти реализацию STN, которая и будет использована в нашей сети.
Наша задача — обозначить и обучить LocNet, обеспечить transformer корректными значениями ? и вставить STN модуль в DAG Tensorflow. transformer генерирует сетку и обеспечивает преобразования и интерполяцию.
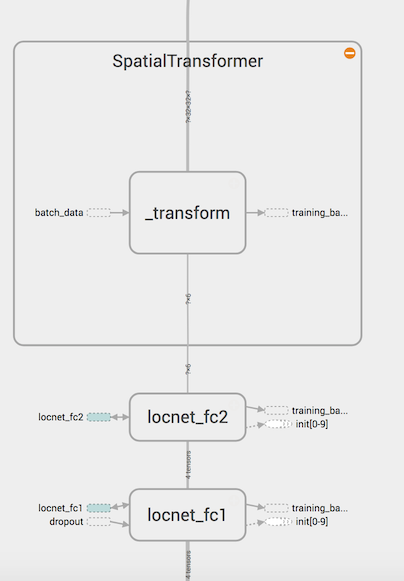
Конфигурация LocNet представлена ниже:
Сверточные слои LocNet:
- Слой 1: Max Pooling. На входе: 32x32x1. На выходе: 16x16x1.
- Слой 2: Convolutional (relu, batch normalization). Kernel : 5x5, 100 фильтров. На входе: 16x16x1 (в наборе из 256). На выходе: 16x16x100.
- Слой 3: Max Pooling. На входе: 16x16x100. На выходе: 8x8x100.
- Слой 4: Convolutional (batch normalization, relu). Kernel : 5x5, 200 фильтров. На входе: 8x8x100 (в наборе из 256). На выходе: 8x8x200.
- Слой 5: Max Pooling. На входе: 8x8x200. На выходе: 4x4x200.
- Слой 6: Дополнительный pooling для multiscale-фич. Kernels: 4, 2 для сверточных слоев 1 и 2 соответственно.
- Слой 7: Вытягивание и конкатенация фич в вектор . На входе: 2x2x100; 2x2x200. На выходе: вектор фич размерностью 400+800 = 1200 для полносвязных слоев.
Fully-connected часть LocNet:
- Слой 8: Fully-connected(batch normalization, relu, dropout). На входе: 1200 признаков (в наборе из 256). 100 нейронов.
- Слой 9: 2х3 матрица ?, которая задает аффинное преобразование. Веса задаются нулями, свободный член — матрицей, похожей на единичную, с единицами на главной диагонали: [[1.0, 0, 0], [0, 1.0, 0]].
- Слой 10: Transformer: Генератор сетки и сэмплер, реализованные в spatial_transformer.py. Этот слой производит изображения с теми же измерениями, что и исходные (32x32x1), применяя к ним аффинное преобразование (таким образом, получается приближенное или повернутое изображение).
Структура сверточных слоев LocNet похожа на IDSIA (хотя LocNet состоит из 2 слоев вместо 3, и в ней мы сначала делаем пуллинг). Более любопытна структура полносвязных слоев:

Обучение и результаты
Проблема использования STN модуля с CNN заключается в необходимости следить за тем, чтобы обе сети не переобучались, что делает процесс обучения сложным и нестабильным. С другой стороны, добавление небольшого количества аугментированных данных (особенно аугментирование яркости) в обучающую выборку позволяет сетям не переобучаться. В любом случае, преимущества перевешивают недостатки: даже без аугментации мы получаем хорошие результаты, а STN+IDSIA превосходят по точности IDSIA без этого модуля на 0,5-1%.
В процессе обучения были использованы следующие параметры:
# TF Parameters
TF_CONFIG = {
'epochs': 20,
'batch_size': 256,
'channels': 1
}
# Omitting the model building phase (discussed earlier in this post)
# ...
# Train / validation datasets, see the previous post.
# No augmentations.
train_val_data = {
'X_train': X_tr_256,
'y_train': y_tr_256,
'X_valid': X_val_256,
'y_valid': y_val_256
}
# Initializing the session and vars:
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
# Skipping details and going to the training:
for i in range(TF_CONFIG['epochs']):
for batch_x, batch_y in batch_generator(train_val_data['X_train'],
train_val_data['y_train'],
batch_size=TF_CONFIG['batch_size']):
_, loss, lr = sess.run([training_operation, loss_operation, learning_rate],
feed_dict={x: batch_x,
y: batch_y,
dropout_conv: 1.0,
dropout_loc: 0.9,
dropout_fc1: 0.3}Уже после 10 эпох мы получаем точность равную 99,3% на validation наборе данных. CNN все еще переобучается, но не забывайте, что мы используем двойную сложную сетку на исходном датасете без его расширения аугментациями. По правде говоря, добавив аугментацию, мне удалось получить точность равную 99,6% на validation сете после 10 итераций (хотя значительно увеличилось время обучения).
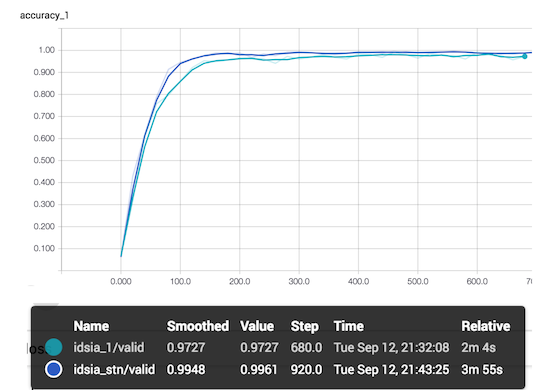
Ниже приведены результаты обучения моделей (idsia_1 — это IDSIA сеть без модуля, idsia_stn — это STN+IDSIA). Это точность всей сети на валидации.

STN+IDSIA показывает себя лучше, чем IDSIA сеть без модуля, хотя, обучается она дольше. Отмечу, что точность на графике выше рассчитана по батчам, а не по всей валидации.
Наконец, вот результат работы STN трансформера после обучения:

Что ж, резюмируем:
- STN — дифференцируемый модуль, который может быть интегрирован в сверточную нейронную сеть. Стандартный юзкейс — это поместить его сразу после батч-генератора, чтобы он мог обучить матрицу преобразований ?, которая минимизирует функцию потерь главного классификатора (IDSIA в нашем случае).
- STN сэмплер применяет аффинное преобразование к исходным изображениям (или карте признаков).
- STN можно рассматривать как альтернативу аугментации изображений, которая является стандартным способом добиться пространственной инвариантности для CNN.
- Добавляя один или несколько STN модулей в CNN усложняет обучение, делает его нестабильным: теперь необходимо следить, чтобы обе (вместо одной) сети не переобучались. Как мне кажется, это одна из причин, почему STN пока не так распространены.
- STN, обученные на аугментированных данных (особенно аугментация яркости) показывают лучшее качество и не переобучаются слишком сильно.

Комментарии (5)

Horus20
06.10.2017 18:49Спасибо за статью! Ждал, но для вечера пятницы слишком сложно :)

Horus20
06.10.2017 19:13А если по существу, вопрос такой. Подходит ли этот способ для детектирования и распознавания частично перекрытых знаков (ветки, другие знак, банальная грязь)?

kirilldaniluk
09.10.2017 16:27На самом деле, подходит. В датасете есть такие, с ними модель неплохо справлялась. А кейс с двумя знаками есть даже в верхней гифке.
Не продакшен — да, в проде для бизнеса нужно что-то типа SSD/YOLO


EndUser
http://www.explainxkcd.com/wiki/index.php/1897 ;-)