Узлы в блокчейн-сети анонимны и работают в условиях отсутствия доверия. В этой ситуации встает проблема верификации данных: как проверить, что в блоке записаны корректные транзакции? Для оценки каждого блока понадобится большое количество времени и вычислительных ресурсов. Решить проблему и упростить процесс помогают деревья Меркла.
Что это такое, как используется, какие существуют альтернативы — расскажем далее.

/ изображение Allison Harger CC
Блоки в биткойн-блокчейне — это перманентно записываемые файлы, которые содержат информацию о проведенных пользователями транзакциях. Дополнительно каждый блок содержит Generation Transaction (или Coinbase Transaction) — это транзакция с информацией об адресе с наградой за решение блока, которая всегда стоит первой в списке.
Все транзакции в блоке представлены как строки в шестнадцатеричном формате (raw transaction format), которые хешируются для получения идентификаторов транзакций (txid). На их основе строится хеш блока, который учитывается последующим блоком, обеспечивая неизменяемость и связность реестра. Единое хеш-значение блока собирается при помощи дерева Меркла, концепция которого была запатентована Ральфом Мерклом (Ralph Charles Merkle) в 1979 году.
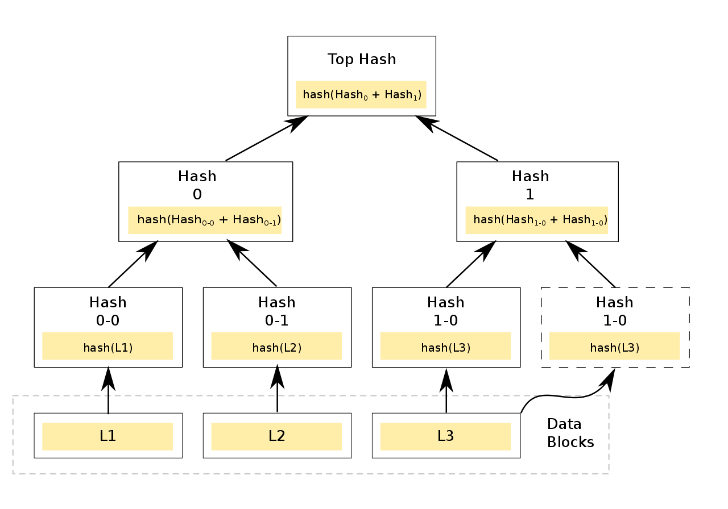
Дерево Меркла, или хеш-дерево, — это двоичное дерево, конечные узлы которого — это хеши транзакций, а внутренние вершины — результаты сложения значений связанных вершин. Вот пример хеш-дерева с тремя транзакциями-листьями:
/ изображение MrTsepa CC
Построение дерева происходит следующим образом:
В биткойн-блокчейне деревья Меркла строятся с использованием двойного хеширования SHA-256. Вот пример хеширования строки hello:
Первый раунд SHA-256:
2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824
Второй раунд:
9595c9df90075148eb06860365df33584b75bff782a510c6cd4883a419833d50
А вот пример реализации деревьев Меркла, используемой биткойном, на Python (результаты работы функции вы можете найти в репозитории на GitHub по ссылке):
?
Файловые системы используют деревья Меркла для проверки информации на наличие ошибок, а распределенные базы данных — для синхронизации записей. В блокчейнах же хеш-деревья позволяют проводить упрощенную верификацию платежей (SPV).
SPV-клиенты, называемые легкими (потому что хранят только заголовки блоков, а не их содержимое), для проверки информации о транзакции не пересчитывают все хеши, а запрашивают доказательство Меркла. Оно состоит из корня и ветви, включающей хеши от запрашиваемой транзакции до корня, поскольку клиенту не нужна информация о других операциях. Сложив запрошенные хеши и сравнив их с корнем, клиент убеждается, что транзакция находится на своем месте.
Такой подход позволяет работать со сколь угодно большими объемами данных, поскольку значительно снижает нагрузку на сеть, так как скачиваются только необходимые хеши. Например, вес блока с пятью транзакциями максимального размера составляет более 500 килобайт. Вес доказательства Меркла в этом же случае не превысит 140 байт.
Двоичные деревья Меркла хорошо подходят для верификации последовательности элементов, поэтому справляются с задачей хранения структуры транзакций. Однако они ограничивают возможности легких клиентов, которые не получают информации о состоянии системы. Например, узнать, какое количество монет есть по указанному адресу, не представляется возможным.
Для обхода ограничения исследователи и разработчики модернизируют уже существующие алгоритмы и разрабатывают новые. Например, в блокчейн-платформе Ethereum используется так называемое префиксное дерево Меркла (Trie). Это структура данных, хранящая ассоциативный массив с ключами.
В отличие от бинарных деревьев Меркла, ключ, идентифицирующий конкретный узел дерева, является «динамическим». Его значение определяется местоположением на дереве и формируется путем соединения символов, присвоенных ребрам графа, проходящим от корня до заданного узла.
В Ethereum заголовок блока содержит сразу три префиксных дерева Меркла: для транзакций, информации об их выполнении и состоянии. Такой подход позволил легким клиентам получать от системы ответы на вопросы: «Есть ли транзакция в указанном блоке?», «Сколько монет на счету?» и «Каким будет состояние системы после выполнения этой транзакции?».
В качестве еще одной альтернативы классическим деревьям Меркла выступает метод комбинирования хеш-значений HashFusion, предложенный Hewlett Packard Labs. Как отмечают в компании, новый подход позволяет рассчитывать значения хешей поэтапно. Компоненты хеша вычисляются сразу, как только данные становятся доступны, а потом объединяются друг с другом при необходимости.
HashFusion подразумевает построение частей хеша с помощью бинарной функции объединения. Она является ассоциативной и некоммутативной, поэтому её можно использовать для объединения хешей в момент формирования. Это позволяет уменьшить объемы памяти, необходимые для их хранения.
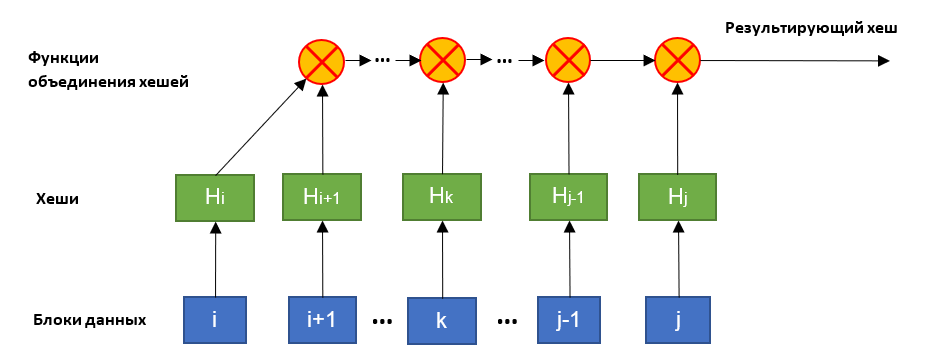
Работа бинарной функции строится следующим образом: она принимает на вход значения хешей (генерируемых классическими хеширующими функциями) и конвертирует их в матрицы целых чисел. После чего матрицы перемножаются, а результат обратно превращается в байтовый массив фиксированной длины.
Представители компании HPE заявляют, что HashFusion реализует более гибкие структуры, по сравнению с деревьями Меркла, которые позволяют обновлять существующие хеши и выборочно удалять/вставлять новые значения. Авторы надеются, что в будущем технология найдет применение в файловых системах, облачных решениях и распределенных реестрах.
Есть и другие алгоритмы, которые ИТ-сообщество разрабатывает с целью оптимизации процессов обработки метаданных и построения деревьев Меркла. Среди них можно выделить решение iSHAKE, автор которого предлагает заменить процесс построения хеш-деревьев внедрением обратимой операции. Она позволит восстанавливать/добавлять и удалять новые значения из структуры. Также можно отметить модифицированный алгоритм организации цифровых подписей eXtended Merkle Signature Scheme (XMSS) и алгоритм SPHINCS.
Большая часть этих предложений находится на стадии тестирования и пока не нашла широкого применения — однако некоторым из них пророчат большое будущее в мире постквантовой криптографии.
P.S. 25 января в Киеве Bitfury проведет бесплатный воркшоп, во время которого будут разобраны практические особенности разработки с помощью Exonum.
Наши специалисты расскажут и покажут, как развернуть собственный блокчейн и как написать сервис. Встреча будет полезна разработчикам на Rust, C++ и JavaScript, делающим первые шаги в блокчейн-разработке, а также тем, кто уже пробовал создавать блокчейн-решения.
Узнать дополнительную информацию о мероприятии и спикерах, а также зарегистрироваться на событие можно по ссылке.
Что это такое, как используется, какие существуют альтернативы — расскажем далее.

/ изображение Allison Harger CC
Дерево Меркла — как оно «выглядит»
Блоки в биткойн-блокчейне — это перманентно записываемые файлы, которые содержат информацию о проведенных пользователями транзакциях. Дополнительно каждый блок содержит Generation Transaction (или Coinbase Transaction) — это транзакция с информацией об адресе с наградой за решение блока, которая всегда стоит первой в списке.
Все транзакции в блоке представлены как строки в шестнадцатеричном формате (raw transaction format), которые хешируются для получения идентификаторов транзакций (txid). На их основе строится хеш блока, который учитывается последующим блоком, обеспечивая неизменяемость и связность реестра. Единое хеш-значение блока собирается при помощи дерева Меркла, концепция которого была запатентована Ральфом Мерклом (Ralph Charles Merkle) в 1979 году.
Дерево Меркла, или хеш-дерево, — это двоичное дерево, конечные узлы которого — это хеши транзакций, а внутренние вершины — результаты сложения значений связанных вершин. Вот пример хеш-дерева с тремя транзакциями-листьями:

/ изображение MrTsepa CC
Построение дерева происходит следующим образом:
- Вычисляются хеши транзакций, размещенных в блоке: hash(L1), hash(L2), hash(L3) и так далее.
- Вычисляются хеши от суммы хешей транзакций, например hash(hash(L1) + hash(L2)). Так как дерево Меркла является бинарным, то число элементов на каждой итерации должно быть четным. Поэтому если блок содержит нечетное количество транзакций, то последняя дублируется и складывается сама с собой: hash (hash(L3) + hash(L3)).
- Далее, вновь вычисляются хеши от суммы хешей. Процесс повторяется, пока не будет получен единый хеш — корень дерева Меркла (merkle root). Он является криптографическим доказательством целостности блока (то есть того, что все транзакции находятся в заявленном порядке). Значение корня фиксируется в заголовке блока.
В биткойн-блокчейне деревья Меркла строятся с использованием двойного хеширования SHA-256. Вот пример хеширования строки hello:
Первый раунд SHA-256:
2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824
Второй раунд:
9595c9df90075148eb06860365df33584b75bff782a510c6cd4883a419833d50
А вот пример реализации деревьев Меркла, используемой биткойном, на Python (результаты работы функции вы можете найти в репозитории на GitHub по ссылке):
?
import hashlib
def merkle_root(lst):
sha256d = lambda x: hashlib.sha256(hashlib.sha256(x).digest()).digest()
hash_pair = lambda x, y: sha256d(x[::-1] + y[::-1])[::-1]
if len(lst) == 1: return lst[0]
if len(lst) % 2 == 1:
lst.append(lst[-1])
return merkle_root([ hash_pair(x, y)
for x, y in zip(*[iter(lst)] * 2) ])Для чего нужны хеш-деревья
Файловые системы используют деревья Меркла для проверки информации на наличие ошибок, а распределенные базы данных — для синхронизации записей. В блокчейнах же хеш-деревья позволяют проводить упрощенную верификацию платежей (SPV).
SPV-клиенты, называемые легкими (потому что хранят только заголовки блоков, а не их содержимое), для проверки информации о транзакции не пересчитывают все хеши, а запрашивают доказательство Меркла. Оно состоит из корня и ветви, включающей хеши от запрашиваемой транзакции до корня, поскольку клиенту не нужна информация о других операциях. Сложив запрошенные хеши и сравнив их с корнем, клиент убеждается, что транзакция находится на своем месте.
Такой подход позволяет работать со сколь угодно большими объемами данных, поскольку значительно снижает нагрузку на сеть, так как скачиваются только необходимые хеши. Например, вес блока с пятью транзакциями максимального размера составляет более 500 килобайт. Вес доказательства Меркла в этом же случае не превысит 140 байт.
Аналоги деревьев Меркла
Двоичные деревья Меркла хорошо подходят для верификации последовательности элементов, поэтому справляются с задачей хранения структуры транзакций. Однако они ограничивают возможности легких клиентов, которые не получают информации о состоянии системы. Например, узнать, какое количество монет есть по указанному адресу, не представляется возможным.
Для обхода ограничения исследователи и разработчики модернизируют уже существующие алгоритмы и разрабатывают новые. Например, в блокчейн-платформе Ethereum используется так называемое префиксное дерево Меркла (Trie). Это структура данных, хранящая ассоциативный массив с ключами.
В отличие от бинарных деревьев Меркла, ключ, идентифицирующий конкретный узел дерева, является «динамическим». Его значение определяется местоположением на дереве и формируется путем соединения символов, присвоенных ребрам графа, проходящим от корня до заданного узла.
В Ethereum заголовок блока содержит сразу три префиксных дерева Меркла: для транзакций, информации об их выполнении и состоянии. Такой подход позволил легким клиентам получать от системы ответы на вопросы: «Есть ли транзакция в указанном блоке?», «Сколько монет на счету?» и «Каким будет состояние системы после выполнения этой транзакции?».
В качестве еще одной альтернативы классическим деревьям Меркла выступает метод комбинирования хеш-значений HashFusion, предложенный Hewlett Packard Labs. Как отмечают в компании, новый подход позволяет рассчитывать значения хешей поэтапно. Компоненты хеша вычисляются сразу, как только данные становятся доступны, а потом объединяются друг с другом при необходимости.
HashFusion подразумевает построение частей хеша с помощью бинарной функции объединения. Она является ассоциативной и некоммутативной, поэтому её можно использовать для объединения хешей в момент формирования. Это позволяет уменьшить объемы памяти, необходимые для их хранения.

Работа бинарной функции строится следующим образом: она принимает на вход значения хешей (генерируемых классическими хеширующими функциями) и конвертирует их в матрицы целых чисел. После чего матрицы перемножаются, а результат обратно превращается в байтовый массив фиксированной длины.
Представители компании HPE заявляют, что HashFusion реализует более гибкие структуры, по сравнению с деревьями Меркла, которые позволяют обновлять существующие хеши и выборочно удалять/вставлять новые значения. Авторы надеются, что в будущем технология найдет применение в файловых системах, облачных решениях и распределенных реестрах.
Есть и другие алгоритмы, которые ИТ-сообщество разрабатывает с целью оптимизации процессов обработки метаданных и построения деревьев Меркла. Среди них можно выделить решение iSHAKE, автор которого предлагает заменить процесс построения хеш-деревьев внедрением обратимой операции. Она позволит восстанавливать/добавлять и удалять новые значения из структуры. Также можно отметить модифицированный алгоритм организации цифровых подписей eXtended Merkle Signature Scheme (XMSS) и алгоритм SPHINCS.
Большая часть этих предложений находится на стадии тестирования и пока не нашла широкого применения — однако некоторым из них пророчат большое будущее в мире постквантовой криптографии.
P.S. 25 января в Киеве Bitfury проведет бесплатный воркшоп, во время которого будут разобраны практические особенности разработки с помощью Exonum.
Наши специалисты расскажут и покажут, как развернуть собственный блокчейн и как написать сервис. Встреча будет полезна разработчикам на Rust, C++ и JavaScript, делающим первые шаги в блокчейн-разработке, а также тем, кто уже пробовал создавать блокчейн-решения.
Узнать дополнительную информацию о мероприятии и спикерах, а также зарегистрироваться на событие можно по ссылке.
Комментарии (11)

FreeMind2000
11.01.2018 14:13концепция которого была запатентована
Не фига себе, концепции оказывается можно патентовать… куда мир катится. © Дебилы.


TimsTims
Для чего вообще нужно складывать хеши? Чтобы усложнить возможность подбора и подмены значений? Почему бы просто не брать сразу один раз один общий хеш от всех транзакций в блоке?
hash(L1 + L2 + L3 + L4 + L5)sndr
Чтобы гарантировать порядок транзакций.
TimsTims
Но порядок транзакций и так будет соблюдён, ведь если их «переставить», то будет уже другой хеш:
hash(L1 + L2 + L3 + L4 + L5) = 111111
hash(L2 + L1 + L3 + L4 + L5) = 222222
unsafePtr
Вы что то путаете. Сложение выполняется операцией XOR. Следовательно значение хеша не измениться если поменять их местами.
Starche
Нет, в en.bitcoin.it/wiki/Protocol_documentation указано, что используется конкатенация. Поиском по d5 = dhash(d1 concat d2) сможете найти нужное место
А XOR бы и при попарном хешировании не менялся при замене L1<->L2
unsafePtr
Верно, верно. Забыл глянуть в спецификации.
Starche
Чтобы для проверки наличия транзакции в блоке не надо было тянуть весь блок.
Достаточно будет только цепочки хэшей от транзакции до корня и хэшей, которые с ними суммировались. Т.е. порядка 2*log(N) транзакций
un1t
Хороший вопрос. Для экономии места на диске, т.к. старые ветки можно удалять, не меняя нижележащие хеши.
Это описано в White Paper от Сатоши Накомото. Пункт 7 — «Reclaiming Disk Space»
«Once the latest transaction in a coin is buried under enough blocks, the spent transactions before
it can be discarded to save disk space. To facilitate this without breaking the block's hash,
transactions are hashed in a Merkle Tree [7][2][5], with only the root included in the block's hash.
Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes do
not need to be stored.»
bitcoin.org/bitcoin.pdf
un1t
P.S. Плюс для упрощенной верификации транзакций. Легким клиентам не нужно скачивать блоки полностью. Это описано в статье.
White Paper — Пункт 8. «Simplified Payment Verification»
jahr
Дерево Меркла проще обновлять во время генерации блока, добавляя/удаляя транзакции, иначе пришлось бы каждый раз пересчитывать хеш от большого объема данных (медленно), а в дереве — можно пересчитать только один путь из нескольких веток (быстро)