11.06.2018 19:12
malkovsky 25 10000 Источник

Предисловие


В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.





UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.

Примечание от автора


На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.

Постановка задачи


Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество $\mathcal{K}$ и функция $f:\mathcal{K}\rightarrow \mathbb{R}$, требуется найти точку $x^*\in \mathcal{K}$, такую что $ f(x)\geq f(x^*)$ для всех $x\in \mathcal{K}$», что обычно записывается например вот так

$f(x)\rightarrow \min_{x\in \mathcal{K}}.$


В теории обычно предполагается, что $f$ — дифференцируемая и выпуклая функция, а $\mathcal{K}$ — выпуклое множество (а еще лучше, если вообще $\mathcal{K}=\mathbb{R}^n$), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).

Немного математики


Допустим пока что нам нужно просто найти минимум одномерной функции

$f(x)\rightarrow \min_{x\in \mathbb{R}}.$


Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли $x^* $ — точка минимума $f^* $, то

$f'(x^*)=0 $


где $f'$ — производная $f$. Этот критерий основан на линейном приближении

$ f(x)\approx f(x^*)+f'(x^*)(x-x^*).$


Чем ближе $x$ к $x^*$, чем точнее это приближение. В правой части — выражение, которое при $f'(x^*)\neq 0$ может быть как больше $f(x^*)$ так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения $f(x)\approx f(x^*)+\nabla f(x^*)^T(x-x^*)$ (здесь и далее $x^Ty=\sum_{i=1}^nx_iy_i$ — стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий

$\nabla f(x^*)=0. $


Величина $\nabla f(x^*)$ — градиент функции $f$ в точке $x^*$. Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.

Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для $f(x)=x^2$ и $f(x)=x^3$


Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.

Квадратичные функции


Квадратичные функции в $\mathbb{R}^n$ — это функция вида

$ f(x) = f(x_1, x_2, \ldots, x_n)=\frac{1}{2}\sum_{i,j=1}^na_{ij}x_ix_j-\sum_{i=1}^n b_ix_i+c $


Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:

$ f(x) = \frac{1}{2}x^TAx-b^Tx+c, $


где $x=(x_1, \ldots, x_n)^T$, $b=(b_1, \ldots, b_n)^T$, $A$ — матрица, у которой на пересечении $i$ строки и $j$ столбца стоит величина
$\frac{1}{2}(a_{ij}+a_{ji})$ ($A$ при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.

Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:

  1. Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
  2. Градиент квадратичной функции — линейная функция, в частности для функции выше

    $ \frac{\partial}{\partial x_i} f(x_1, x_2, \ldots, x_n) = a_{ii} x_i + \sum_{j\neq i}\frac{1}{2}(a_{ij}+a_{ji})x_j -b_i, $


    Или в матричной форме

    $ \nabla f(x) = Ax-b, $


    Таким образом система $\nabla f(x)=0$ — линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что $\nabla f(x^*)=0$ — необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.

Полезные свойства градиента


Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?

Попробуем пока решить более простую задачу: дана точка $x$, найти точку $\bar{x}$ такую, что $f(\bar{x})<f(x)$. Давайте возьмем точку рядом с $x$, опять же используя линейное приближение $f(\bar{x})\approx f(x)+\nabla f(x)^T(\bar{x}-x)$. Если взять $\bar{x}=x-\alpha\nabla f(x)$, $ \alpha>0$ то мы получим

$ f(\bar{x})\approx f(x)-\alpha\|\nabla f(x)\|^2>f(x). $


Аналогично, если $ \alpha<0 $, то $f(\bar{x})$ будет больше $f(x)$ (здесь и далее $||x||=\sqrt{x_1^2+x_2^2+\ldots+x_n^2}~$). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых $\alpha$. Подытоживая вышесказанное, если $\nabla f(x)\neq 0$, то градиент указывает направление наибольшего локального увеличения функции.

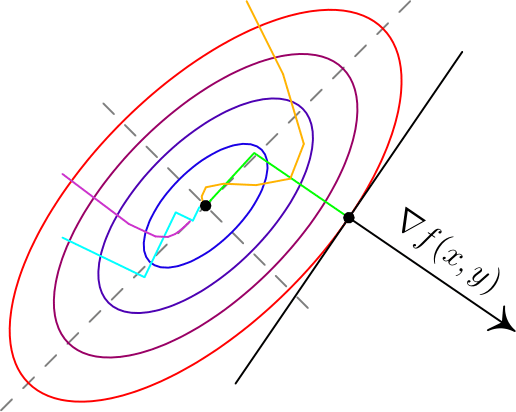
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.



Обратите внимание, что для поверхности, заданной уравнением вида $f(x)=c$, $\nabla f(x) $ задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).

Градиентный спуск


До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке $x$ получать точку $\bar{x}$ с меньшим значением функции $ f$. Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k). $


Величина $\alpha_k$ называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора $\alpha_k$: если $\alpha_k$ — очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же $\alpha_k$ очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если

$ \|\nabla f(x)-\nabla f(y)\|\leq L\|x-y\| $


для всех $x,y$, то $\alpha_k< \frac{2}{L}$ гарантирует убывание $f(x_k)$.

Анализ для квадратичных функций


Если $A$ — симметричная обратимая матрица, $Ax^*=b$, то для квадратичной функции $f(x)=\frac{1}{2}x^TAx-b^Tx+c$ точка $x^*$ является точкой минимума (UPD. при условии, что этот минимум вообще существует — $f$ не принимает сколько угодно близкие к $-\infty$ значения только если $A$ положительно определена), а для метода градиентного спуска можно получить следующее

$ x_{k+1}-x^* = x_k-\alpha_k \nabla f(x_k)-x^* = x_k-\alpha_k(Ax_k-b)-x^*= $


$ (x_k-x^*)-\alpha_kA(x_k-x^*)=(I-\alpha_k A)(x_k-x^*), $


где $ I $ — единичная матрица, т.е. $ Ix=x$ для всех $ x$. Если же $\alpha_k\equiv\alpha$, то получится

$ \|x_{k}-x^*\|=\|(I-\alpha A)^k(x_0-x^*)\|\leq \|I-\alpha A\|^k \|x_0-x^*\|. $


Выражение слева — расстояние от приближения, полученного на шаге $k$ градиентного спуска до точки минимума, справа — выражение вида $\lambda^k \beta$, которое сходится к нулю, если $|\lambda|<1$ (условие, которое я писал на $\alpha$ в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.

Модификации градиентного спуска


Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые

Инерционные или ускоренные градиентные методы


Все методы такого класса выражаются в следующем виде

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k)+\beta_k(x_k-x_{k-1}). $


Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:

  1. Они практически не усложняют обычный градиентный спуск в вычислительном плане.
  2. При аккуратном подборе $\alpha_k, \beta_k$ такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.

Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе $\alpha_k, \beta_k$ не зависят от $k$ и аккуратно подбираются в зависимости от целевой функции. Стоит отметить, что $\alpha_k$ может быть какой угодно, а $\beta_k$ — обычно лишь чуть-чуть меньше единицы.

Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.

Метод Чебышева


Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство

$ x_{k+1}-x^* = (I-\alpha_k A) (x_k-x^*)=\ldots= $


$ (I-\alpha_kA)(I-\alpha_{k-1}A)\ldots(I-\alpha_1A)(x_0-x^*)=P_k(A)(x_0-x^*), $


где $P_k$ — некоторый многочлен степени $k$. Почему бы не попробовать подобрать $\alpha_k$ таким образом, чтобы $P_k(A)(x_0-x^*)$ было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы $P_k$ был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка

$ T_{n+1}(x)=2xT_n(x)-T_{n-1}(x), $


поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления $\alpha_k,\beta_k$ не зависит ни от $k$, ни от размера пространства $n$.

Метод сопряженных градиентов


Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы $A$ размера $n\times n$ существует многочлен $P$ степени не больше $n$, для которого $P(A)=0$. Чем это интересно? Все дело в том же равенстве

$ x_{k+1}-x^* = P_k(A)(x_0-x^*). $


Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности $A$. Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом

  1. Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
  2. Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.

Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время $\mathcal{O}(n^2)$, однако для со специальной реализацией это можно сделать за $\mathcal{O}(m) $, где $m$ — количество ненулевых элементов в $A$. Учитывая сходимость метода сопряженных градиентов не более, чем за $n$ итерации получаем общую сложность алгоритма $\mathcal{O}(nm)$, что во всех случаях не хуже $\mathcal{O}(n^3)$ для метода Гаусса или Холесского, но намного лучше в случае, если $m<<n^2$, что не так редко встречается.

Метод сопряженных градиентов хорошо работает и в случае, если $f$ не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций

Метод Нестерова


Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k+\beta_k(x_k-x_{k-1}))+\beta_k(x_k-x_{k-1})), $


при этом не предполагается какого-то сложного подсчета $\alpha_k,\beta_k$ как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.

Стохастический градиентный спуск


Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции $g(x, \theta)$ такой, что $E_\theta g(x,\theta)=\nabla f(x)$ ($E_\theta$ — математическое ожидание по случайной величине $\theta$), таким образом стохастический градиентный спуск имеет вид

$ x_{k+1}=x_k-\alpha_kg(x_k, \theta_k). $


$\theta_k$ — это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции

$ f(x)=\frac{1}{2m}\sum_{j=1}^m\|x-y_j\|^2,~~\nabla f(x)=\frac{1}{m}\sum_{j=1}^m(x-y_j) $


и

$ g(x, i)=x-y_i. $


Если $i$ принимает значения $1,\ldots, m$ равновероятно, то как раз в среднем $g$ — это градиент $f$. Этот пример показателен еще и следующим: сложность вычисления градиента в $m$ раз больше, чем сложность вычисления $g$. Это позволяет стохастическому градиентному спуску делать за одно и то же время в $m$ раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.

Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией $g$.

Субградиентный спуск


Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция $f$ выпукла тогда и только тогда, когда выполняется $f(y)\geq f(x)+\nabla f(x)^T(y-x)$ для всех $x, y$ . Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки $x$ обязательно найдется такой вектор $g$, что $f(y)\geq f(x)+g^T(y-x)$ для всех $y$. Такой вектор $g$ принято называть субградиентом $f$ в точке $x$, множество всех субградиентов в точки $x$ называют субдифференциалом $x$ и обозначают $\partial f(x)$ (несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае $g$ — это число, а вышеуказанное свойство просто означает, что график $f$ лежит выше прямой, проходящей через $(x, f(x))$ и имеющей тангенс угла наклона $g$ (смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.



Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию $ReLU(x)=\max(0, x)$ любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция $ReLU$ выпукла, но многослойная нейронная сеть, содержащая $ReLU$, невыпукла и недифференцируема). В качестве примера, для функции $f(x)=|x|$ субдифференциал вычисляется очень просто

$ \partial f(x)=\begin{cases} 1, & x>0, \\ -1, & x < 0, \\ [-1, 1], & x=0. \end{cases} $



Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции $f(x)=|x|$. Даже отсутствие производной в одной точке ломает сходимость:

  1. Допустим мы начали из точки $x_0$.
  2. Шаг субградиентного спуска:

    $ x_{k+1}=\begin{cases} x_{k}-1, & x>0, \\ x_k+1, & x < 0, \\ ??? & x=0. \end{cases} $

  3. Если $x_0>0$, то первые несколько шагов мы будет вычитать единицу, если $x_0<0$, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале $[0, 1)$, из которого попадем в $[-1, 0)$, а дальше будем прыгать между двумя точками этих интервалов.

В теории для субградиентного спуска рекомендуется брать последовательность шагов

$ \alpha_k=\frac{1}{(k+1)^c}. $


Где $c$ обычно $1$ или $\frac{1}{2}$. На практике я часто видел успешное применение шагов $\alpha_k=e^{-ck}$, хоть и для таких шагов вообще говоря не будет сходимости.

Proximal методы


К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция $f$, представимая в виде суммы $f(x)=\varphi(x)+h(x)$, где $\varphi$ — дифференцируемая выпуклая функция, а $h(x)$ — выпуклая, для которой существует специальный proximal-оператор $prox_h(x)$ (в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для $\varphi$ остаются и для градиентного спуска для $f$, если после каждой итерации применять этот proximal-оператор для текущей точки $x_k$, другими словами общий вид proximal-метода выглядит так:

$ x_{k+1}=prox_{\alpha_kh}(x_k-\alpha_k\nabla \varphi(x_k)) $


Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:
  1. $h(x)$ — индикатор-функция выпуклого множества $\mathcal{K}$, то есть

    $ h(x)=\begin{cases} 0, & x\in \mathcal{K},\\ +\infty, & x\notin \mathcal{K}.\\ \end{cases} $


    В этом случае $prox_{\alpha_kh}(x)$ — это проекция на множество $\mathcal{K}$, то есть «ближайшая к $x$ точка множества $\mathcal{K}$». Таким образом, мы ограничиваем градиентный спуск только на множество $\mathcal{K}$, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате

    $ l_i\leq x_i\leq r_i $


  2. $h(x)=\lambda \|x\|_1=\lambda\sum_{i=1}^n|x_i|$ — $\ell_1$-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):

    $ [prox_{\alpha h}(x)]_i=\begin{cases} x_i-\alpha, & x_i>\alpha,\\ x_i+\alpha, & x_i <-\alpha,\\ 0, & x_i\in [-\alpha, \alpha], \end{cases} $


    что довольно просто вычислить.

Заключение


На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.

Использованная / рекомендованная литература


Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory

Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск

Комментарии (25)


  1. capjdcoder
    12.06.2018 00:21
    #18762067

    Оффтоп: а почему под Safari не видно формул? Вот совсем? На Chrome все есть, все норм.


    1. slovak
      12.06.2018 00:52
      #18762099
      +1

      В мобильном хроме тоже ничего не видно. Поправьте пожалуйста!


  1. telobezumnoe
    12.06.2018 02:13
    #18762223

    эх, ностальгия, нахождение экстремумов, золотое сечение, градиентный метод, линейное программирование, канторович с фанерным трестом… жаль спустя 15 лет всё вылетело из головы, хочется освежить память, но мобильный браузер ни в какую не хочет отображать формулы)


    1. Dark_Daiver
      12.06.2018 07:42
      #18762467
      +2

      Если интересно, то могу посоветовать отличную книжку Numerical Optimization. Книжка фокусируется на минимизации гладких нелинейных функций (т.е. proximal gradient там нет, насколько я помню). На мой взгляд идеальная точка старта если «хочется освежить память»
      Еще есть Boyd Convex Optimization но это уже посложнее


  1. Dark_Daiver
    12.06.2018 07:30
    #18762459
    +2

    требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента

    При всем уважении, в том же BFGS кроме вычисления градиента требуется только несколько матричных умножений и скалярных произведений. Практически всегда градиент более затратен по вычислениям. Другое дело, что хорошо объяснить как работает BFGS достаточно сложно (лично я хороших и в то же время прозрачных объяснений не встречал)


    1. malkovsky Автор
      12.06.2018 15:36
      #18763731

      Согласен, тут я немного приврал. Вообще говоря для квадратичных функций поведение BFGS схоже с методом сопряженных градиентов, по крайней мере сходится за конечное число шагов, но не уверен, что умеет использовать разреженность матриц. В нелинейном случае, если не считать вычисление градиента, то метод сопряженных градиентов (а остальные уж тем более) не делают умножений матрица-вектор. Вроде бы понятно, что если размерность пространства больше ~10^4-10^5, то это становится критичным.


      1. Dark_Daiver
        12.06.2018 16:24
        #18763919

        Важно что BFGS собирает намного больше информации о ландшафте ф-ии, т.к. «помнит» больше шагов

        но не уверен, что умеет использовать разреженность матриц

        Ему это и не нужно. Если хранить аппроксимированный обратный гессиан слишком дорого, то есть LBFGS который хранить лишь к векторов и стоимость шага становится близкой к CG.
        Ну и на практике BFGS практически всегда дефолтный алгоритм во всяких библиотеках для оптимизации, типа scipy.optimize, в отличии от CG


  1. Dark_Daiver
    12.06.2018 08:13
    #18762507
    +1

    Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.

    А можно вместо обзора подробный разбор одного из методов? С интерпретацией картиночками и выводом формул. Желательно чего-то посложнее, типа BFGS или proximal gradient. А то на хабре почти нет хороших материалов по оптимизации, а у автора явно есть хорошие знания по теме =(


  1. KonkovVladimir
    12.06.2018 08:27
    #18762531
    +1

    Оптимизация в многомерном пространстве важная тема в квантовой химии.

    К затронутые в статье методы имеют низкую эффективность и устойчивость в (3N-5)-мерном пространстве, где N>10 количество атомов.
    BFGS это минимум что можно можно использовать, rational function optimization (RFO) и trust radius model (TRM) или geometry optimization using direct inversion in the iterative subspace (GDIIS) или fast inertial relaxation engine (FIRE) более эффективны.
    spindynamics.org/documents/cqc_lecture_6.pdf
    users.jyu.fi/~pekkosk/resources/pdf/FIRE.pdf

    Порой кроме локальных минимумов также требуется найти седловую точку первого порядка и «кратчайший путь» через нее между двумя локальными минимумами, что позволяет определить скорости химических реакций.
    Но это совсем другая тема.


    1. malkovsky Автор
      12.06.2018 20:19
      #18764645
      +1

      Спасибо, поизучаю на досуге. Я правильно понимаю, что имелось в виду размерность >= 300000? Мне казалось, что при такой размерности квазиньютоновские методы становятся довольно громоздкими.


      1. KonkovVladimir
        13.06.2018 06:25
        #18765889

        Дело в другом. В квантовой химии расчет энергии в точке имеет сложность n^7 иногда n^4 (n — количество электронов), градиент и гессиан еще сложнее, поэтому если какой-то метод может сократить количество шагов оптимизации вдвое, то это уже не плохо.
        N >= 300000 это молекулярная механика, там взаимодействия между атомами описываются набором подгоночных под эксперимент параметров, волновая функция там не вычисляется.
        Точное вычисление волновой функции это экспоненциально сложная задача, вряд ли ее можно решить на классическом компьютере для n>50, приближенное решение ее можно имеет полиномиальную сложность довольно высокого порядка. По поводу «сложности» квазиньютоновских методов там и не парятся вообще.


  1. slava_k
    12.06.2018 11:13
    #18762835

    Спасибо за труд, буду рад видеть продолжение.


    1. geisha
      12.06.2018 13:35
      #18763263

      Тоже.


  1. GreySS
    12.06.2018 14:34
    #18763475

    Спасибо за статью. Могли бы вы добавить список используемой литературы?


    1. malkovsky Автор
      12.06.2018 15:21
      #18763673

      Добавил. Если вдруг нужно что-то конкретное — спрашивайте, может знаю, что порекомендовать.


  1. Costic
    12.06.2018 15:36
    #18763733

    Proximal методы — метод (пошагового) приближения, как мне кажется.
    А где список литературы и ссылок? </зануда off>

    Вы упомянули про диссертацию, уточните, пожалуйста, тему, если она имеет отношение к статье. Какая в ней научная новизна?
    Вы несколько раз упоминаете нейронные сети, а можно поподробнее (или ещё статью) про применение методов оптимизации в этим сетям? На мой взгляд все эти сети малопригодны, т.к. по сути являются системой уравнений порядка n и годятся только для интерполяции и ближайшей экстраполяции. Структурные изменения они неспособны прогнозировать или я не прав?

    К вопросу сходимости. В 1998 я применял подобные методы для экономической задачки. Получил 2 экстремума, один локальный. И градиент привёл меня сначала в локальный. Графически это примерно так выглядело (сокращены параметры до 2 + динамика). image
    Стохастически (монте-карло вроде бы) определил наличие глобального экстремума. А что делать если таких локальных экстремумов много? Предварительно сгладить? Понизить порядок, думаю.


    1. malkovsky Автор
      12.06.2018 16:09
      #18763857

      Список литературы добавил.

      Диссертация (к. ф.-м. н.): Рандомизированные алгоритмы распределения ресурсов в адаптивных мультиагентных системах — если в кратце, то я занимался распределенной децентрализованной оптимизацией, то есть такими алгоритмами, которые не требуют какого-то «центрального» вычислительного узла, имеющего информацию о всей сети в целом.

      По нейронным сетям есть замечательная экспериментальная статья здесь же на хабре. Ключевая связь между градиентными методами и обучением нейронных сетей — это так называемый «метод обратного распространения ошибки» (backpropagation). Про него мне кажется можно посмотреть вот здесь и здесь.

      Формально нейронные сети — это класс функций, который теоретически умеет приближать все, что угодно (вот тут упомянуты две теоремы на этот счет, страница 4), к сожалению идеально подобрать параметры приближения — довольно сложно. При применении градиентных методов этот как раз выражается в частом застревании в локальных минимумах — это известная проблема, к сожалению какого-то универсального решения нет. Есть генетические методы, метод отжига, метод муравьиных колоний и т.п., которые частично умеют это обходить, но они требуют больше вычислений.


      1. Dark_Daiver
        12.06.2018 16:32
        #18763951

        При применении градиентных методов этот как раз выражается в частом застревании в локальных минимумах — это известная проблема

        Вот довольно спорно, на самом деле. Тут пишут что глобальный минимум не особо нужен при обучении ANN
        Finally, we prove that recovering the global minimum becomes harder as the network size increases and that it is in practice irrelevant as global minimum often leads to overfitting

        Авторы весьма авторитетны.


        1. malkovsky Автор
          12.06.2018 16:49
          #18764029

          Да, для нейронных сетей это может быть не так важно, но все-таки оптимизация не только в них применяется, а проблема локальных минимумов появилась задолго до нейронок.


  1. ignorance
    12.06.2018 18:12
    #18764291

    Спасибо за статью.
    Поправьте, пожалуйста, формулы в разделе «Анализ для квадратичных функций»
    x(k+1) — x* — там дальше пропущен символ градиента
    И в Abs(x(k)-x*) — там изначально ведь идет произведение (I-a(k)A) для всех k?
    А дальше оценка неясна — I-a — величины несоразмерные, вероятно имелось в виду I-aA? И какая норма матрицы используется? И почему lambda меньше 1? Вероятно, это следствие критерия Липшица, но я не вижу каким образом.
    Понятно, что вопросы сугубо теоретические. Но хотелось бы понять, не прибегая к литературе. Спасибо.


    1. malkovsky Автор
      12.06.2018 18:21
      #18764311

      Поправил. Норма везде подразумевается операторная т.е. ||A||=sup ||Ax||/||x|| (x!=0), такая норма гарантирует ||Ax||<=||A|| ||x|| для всех х. Для симметричных матриц — это просто спектральный радиус, т.е. наибольшее по абсолютной величине собственное число. Если у матрицы A спектр (множество собственных чисел) на отрезке [m, L] (хотя бы 0, так как в противном случае функция не ограничена снизу, а также у вещественных симметричных матриц собственные числа вещественные), то у матрицы I-aA — на отрезке [1-aL, 1-mL]. Соответственно 1-aL>-1 если a<2/L. Если m>0, то 1-mL < 1, что верно для положительно определенных матриц, но с m=0 градиентный спуск тоже корректно работает, но чуть сложнее это показать. К слову L в этом случае как раз будет константой липшица для градиента f.


      1. olgerdovich
        12.06.2018 21:58
        #18764933

        Вы с «x!=0», пожалуйста, поаккуратнее, непрограммисту так мозг можно взорвать: для меня "!" после числа/переменной перед равенством — это значение факториала числа/переменной.


      1. malkovsky Автор
        13.06.2018 12:43
        #18767733

        Пардон, здесь описался, не 1-mL, а 1-am.


  1. olgerdovich
    12.06.2018 22:19
    #18765023

    У вас хорошая публикация; как я понял, это своего рода конспект «для себя», сделанный «как для людей», и я с удовольствием собрался его проштудироапть с карандашом и тетрадью. Выделен смысл, убраны технические детали за исключением нужных. Для тех, кто не математик, а пользуется математикой для своих задач. Перед детальным анализом я, все же, посоветую: по возможности, нумеруйте формулы, чтобы к ним можно было отсылаться.

    К сожалению, сейчас я обнаруживаю, что с мобильного андроидного устройства даже в десктопном режиме дальше сложно высказывать предложения (затруднения с формулами), поэтому вернусь чуть позже комментарием к этому своему сообщению.


  1. SkylineIT
    13.06.2018 14:38
    #18768437

    Вкину немного своего экспириенса :)

    Метод покоординатного спуска
    Идея данного метода в том, что поиск происходит в направлении покоординатного спуска во время новой итерации. Спуск осуществляется постепенно по каждой координате. Количество координат напрямую зависит от количества переменных.
    Для демонстрации хода работы данного метода, для начала необходимо взять функцию z = f(x1, x2,…, xn) и выбрать любую точку M0(x10, x20,…, xn0) в n пространстве, которая зависит от числа характеристик функции. Следующим шагом идет фиксация всех точек функции в константу, кроме самой первой. Это делается для того, чтобы поиск многомерной оптимизации свести к решению поиска на определенном отрезке задачу одномерной оптимизации, то есть поиска аргумента x1.
    Для нахождения значения данной переменной, необходимо производить спуск по этой координате до новой точки M1(x11, x21,…, xn1). Далее функция дифференцируется и тогда мы можем найти значение новой следующий точки с помощью данного выражения:

    image

    После нахождения значения переменной, необходимо повторить итерацию с фиксацией всех аргументов кроме x2 и начать производить спуск по новой координате до следующей новой точке M2(x11,x21,x30…,xn0). Теперь значение новой точки будет происходить по выражению:

    image

    И снова итерация с фиксацией будет повторяться до тех пор, пока все аргументы от xi до xn не закончатся. При последней итерации, мы последовательно пройдем по всем возможным координатам, в которых уже найдем локальные минимумы, поэтому целевая функция на последний координате дойдет до глобального минимума. Одним из преимуществ данного метода в том, что в любой момент времени есть возможность прервать спуск и последняя найденная точка будет являться точкой минимума. Это бывает полезно, когда метод уходит в бесконечный цикл и результатом этого поиска можно считать последнюю найденную координату. Однако, целевая установка поиска глобального минимума в области может быть так и не достигнута из-за того, что мы прервали поиск минимума (см. Рисунок 1).

    image
    Рисунок 1 – Отмена выполнения покоординатного спуска

    Исследование данного метода показали, что каждая найденная вычисляемая точка в пространстве является точкой глобального минимума заданной функции, а функция z = f(x1, x2,…, xn) является выпуклой и дифференцируемой.
    Отсюда можно сделать вывод, что функция z = f(x1, x2,…, xn) выпукла и дифференцируема в пространстве, а каждая найденная предельная точка в последовательности M0(x10, x20,…, xn0) будет являться точкой глобального минимума (см. Рисунок 2) данной функции по методу покоординатного спуска.

    image
    Рисунок 2 – Локальные точки минимума на оси координат

    Можно сделать вывод о том, что данный алгоритм отлично справляется с простыми задачами многомерной оптимизации, путём последовательно решения n количества задач одномерной оптимизации, например, методом золотого сечения.

    Ход выполнения метода покоординатного спуска происходит по алгоритму описанного в блок схеме (см. Рисунок 3). Итерации выполнения данного метода:
    • Изначально необходимо ввести несколько параметров: точность Эпсилон, которая должна быть строго положительной, стартовая точка x1 с которой мы начнем выполнение нашего алгоритма и установить Лямбда j;
    • Следующим шагом будет взять первую стартовую точку x1, после чего происходит решение обычного одномерного уравнения с одной переменной и формула для нахождения минимума будет, где k = 1, j=1:
    image
    • Теперь после вычисления точки экстремума, необходимо проверить количество аргументов в функции и если j будет меньше n, тогда необходимо повторить предыдущий шаг и переопределить аргумент j = j + 1. При всех иных случаях, переходим к следующему шагу.
    • Теперь необходимо переопределить переменную x по формуле x (k + 1) = y (n + 1) и попытаться выполнить сходимость функции в заданной точности по выражению:
    image
    Теперь от данного выражения зависит нахождение точки экстремума. Если данное выражение истинно, тогда вычисление точки экстремума сводится к x*= xk + 1. Но часто необходимо выполнить дополнительные итерации, зависящие от точности, поэтому значения аргументов будет переопределено y(1) = x(k + 1), а значения индексов j =1, k = k + 1.

    image
    Рисунок 3 – Блок схема метода покоординатного спуска

    Итого, у нас имеется отличный и многофункциональный алгоритм многомерной оптимизации, который способен разбивать сложную задачу, на несколько последовательно итерационных одномерных. Да, данный метод достаточно прост в реализации и имеет легкое определение точек в пространстве, потому что данной метод гарантирует сходимость к локальной точке минимума. Но даже при таких весомых достоинствах, метод способен уходить в бесконечные циклы из-за того, что может попасть в своего рода овраг.
    Существуют овражные функции, в которых существуют впадины. Алгоритм, попав в одну из таких впадин, уже не может выбраться и точку минимума он обнаружит уже там. Так же большое число последовательных использований одного и того же метода одномерной оптимизации, может сильно отразиться на слабых вычислительных машинах. Мало того, что сходимость в данной функции очень медленная, поскольку необходимо вычислить все переменные и зачастую высокая заданная точность увеличивает в разы время решения задачи, так и главным недостатком данного алгоритма – ограниченная применимость.
    Проводя исследование различных алгоритмов решения задач оптимизации, нельзя не отметить, что огромную роль играет качество данных алгоритмов. Так же не стоит забывать таких важных характеристик, как время и стабильность выполнения, способность находить наилучшие значения, минимизирующие или максимизирующие целевую функцию, простота реализации решения практических задач. Метод покоординатного спуска прост в использовании, но в задачах многомерной оптимизации, чаще всего, необходимо выполнять комплексные вычисления, а не разбиение целой задачи на подзадачи.