С 10 по 15 июля в Стокгольме прошла конференция ICML, одна из крупнейших в мире в области машинного обучения. В этом году ее посетило рекордное количество участников – 7000. Среди них были и сотрудники Яндекса, которые представляли технологии CatBoost и DeepHD, сервисы Толока, Дзен и Переводчик, направление беспилотных автомобилей и другие продукты. Сегодня они поделятся с читателями Хабра подборкой докладов, которые запомнились им больше всего.
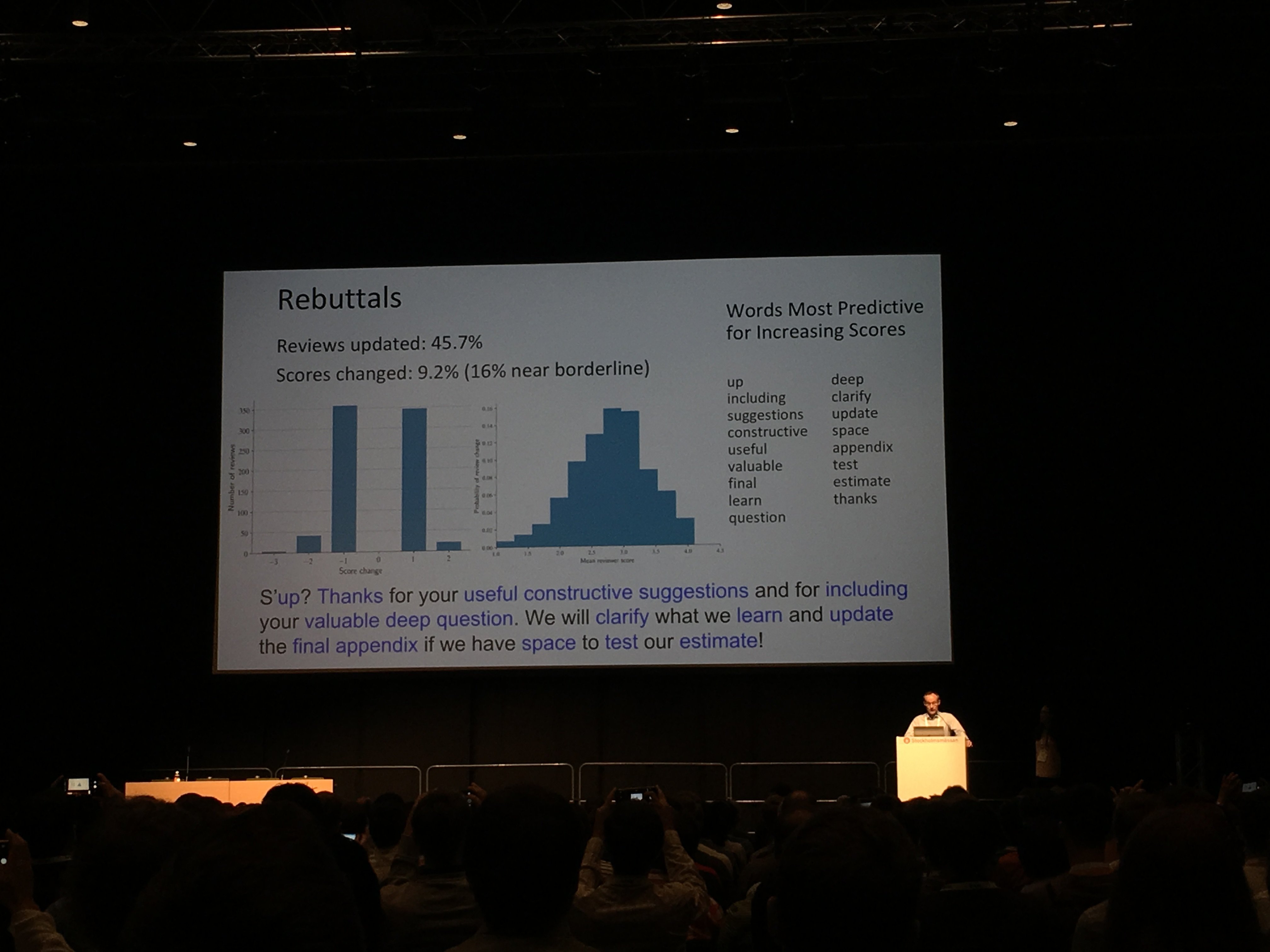
Кстати, на фото выше шутка организаторов – это статистика по словам из писем тех, кто отправлял свой доклад на конференцию. Точнее, из писем с ответами на критику рецензентов, которые привели к приёму доклада. Тут же приведен «идеальный» ответ, с точки зрения машинного обучения. Но мы отвлеклись, переходим к обзору пяти лучших докладов (все заголовки кликабельны и ведут на работы докладчиков).
Один из самых интересных докладов про генеративные модели и обучение представлений на конференции.
Предыстория
Вариационные автокодировщики (VAE) пытаются моделировать распределение наблюдаемых данных следующим процессом:
1. Вначале из некоторого априорного распределения выбирают «скрытую» переменную .
2. Затем с помощью нейросети-декодера c параметрами из нее получают параметры распределения .
3. Из полученного распределения выбирают очередной объект.
Такая формулировка позволяет строить из простых кирпичиков весьма сложные модели и хорошо интерпретируемые представления. Например, если – это двумерное нормальное распределение, а – 724-мерный бернуллевский вектор, VAE удачно выучивает многообразие цифр MNIST.
Если в полученном пространстве на месте точек нарисовать матожидание соответствующих распределений , мы увидим, что модель аккуратно уложила многообразие цифр на плоскость.

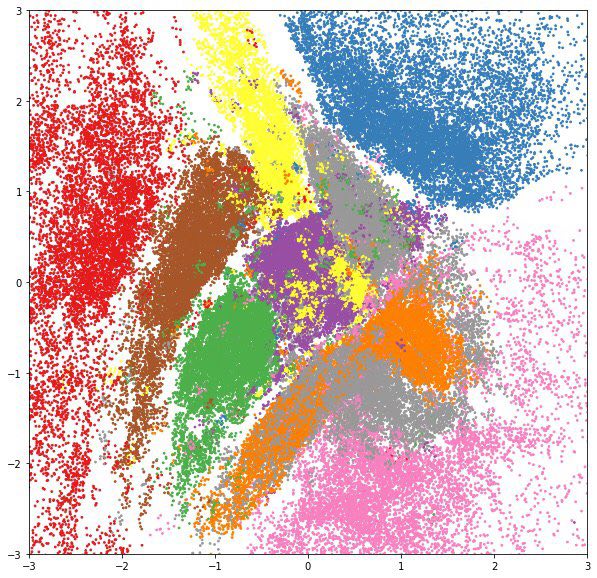
А если для каждого класса цифр из тестового набора нарисовать апостериорное распределение отдельным цветом, мы увидим, что скрытые переменные выучивают очень полезные представления: на таких двухмерных признаках куда проще научить классификатор, и ему точно не понадобится много размеченных данных.
Правдоподобие наблюдаемых данных в такой модели записывается в виде:
Если задается глубокой нейросетью, у нас нет никаких шансов взять этот интеграл аналитически, поэтому прямая максимизация правдоподобия оказывается невозможной. Вместо этого используют так называемый вариационный байесовский вывод:
– Для каждого объекта обучающей выборки вводится вспомогательное распределение , описываемое параметром . Задача – как можно точнее аппроксимировать апостериорное распределение . Другими словами, оно предсказывает из каких был получен наблюдаемый объект .
– Записывается нижняя оценка на логарифм правдоподобия выборки:
Эта нижняя оценка также называется ELBO (Evidence Lower Bound) – нижняя граница обоснованности. Она в точности равна логарифму правдоподобия если .
– Полученная оценка максимизируется по и стохастическим градиентным спуском, при этом стохастический градиент внутреннего интеграла получается либо с помощью reparametrization trick, либо с помощью log-derivative trick (он же score function estimator, он же REINFORCE).
Поскольку хранить и оптимизировать параметры для каждого объекта выборки слишком дорого, вводится дополнительная нейросеть-энкодер, которая принимает на вход и возвращает . Такой подход называется амортизированным вариационным выводом. Именно использование амортизированного вывода позволило учить сложные иерархические вероятностные модели на больших данных.
Слишком умный декодер
Когда мы ограничиваем простым семейством распределений (например нормальными распределениями с диагональными матрицами ковариации), выучивает полезные представления данных. Простой арифметикой в пространстве можно менять прическу у человека на фотографии или смешивать мелодии.

Однако, простые модели, в которых все элементы вектора независимы при условии , не очень хорошо справляются со сложными данными, например с текстами или изображениями в высоком разрешении. Разумно пытаться использовать в качестве сложные «нейросетевые» распределения: авторегрессионные сети, такие как WaveNet или PixelCNN, нормализующие потоки, например, RealNVP, вложенные VAE, или даже -GAN.
При попытке обучить VAE с такими декодерами исследователи сталкиваются с большими трудностями: «слишком умный» декодер сам «съедает» всю энтропию в данных и вообще перестает смотреть на скрытую переменную. и оказываются независимыми, и получить полезные представления из скрытой переменной не получается. В разных статьях были предложены способы обойти эту проблему, но в основном они сводятся либо к упрощению декодера, либо к разным хакам при обучении. Авторы рассматриваемой статьи предлагают первое фундаментальное объяснение причин этого эффекта и способы борьбы с ним.
Главные идеи статьи
– Аппарат из Information Bottleneck Theory применяется к задаче обучения представлений. Авторы предлагают рассмотреть взаимную информацию между и . Когда взаимная информация равна , скрытая переменная сжимает данные без потерь: мы получаем идеальный автокодировщик. Когда взаимная информация равна нулю, скрытая переменная независима от данных, декодер «сожрал» всю энтропию. Для того чтобы обучить полезные представления, мы хотим получить вариант посередине: скрытая переменная должна описать важную информацию об объекте (например, форма лица, цвет глаз, ...) и выбросить детали (цвета конкретных пикселей, текстуры).
– Предлагается смотреть на VAE с альтернативной позиции: пусть теперь основная часть модели , а и – аппроксимации для и маржинального распределения .
– Для фиксированного рассматриваются нижняя и верхняя оценки на взаимную информацию, зависящие от и :
где – энтропия данных, – потери при сжатии и – KL-дивергенция между и

Каждому семейству моделей соответствует выпуклое множество точек в RD пространстве, форма этого множества зависит от «баланса сил» между энкодером и декодером.
– Показано, что оптимизация ELBO эквивалента минимизации , то есть поиску точки с коэффициентом касательной на границе множества. Если декодер достаточно гибкий и не в состоянии хорошо аппроксимировать , модели не выгодно вкладывать дополнительную информацию в латентную переменную: с точки зрения ELBO дешевле выучить ее декодером.
– Для построения наиболее полезных представлений, авторы предлагают оптимизировать , где – гиперпараметр, отвечающий за баланс между энкодером и декодером.
– Авторы экспериментально показали, что варьируя , можно выучивать представления с разным уровнем абстракции: от автоэнкодера (), который сжимает данные без потерь, до «автодекодера» (), который полностью игнорирует данные. Подобрав значение , можно получить «семантический энкодер», который кодирует только общую форму объекта, или «синтаксический энкодер», который способен восстановить мелкие детали. При этом все эксперименты проводились с супермощным авторегрессионным PixelCNN++ декодером, который до этого не удавалось применять в VAE.

Авторы ставят перед собой задачу отображения музыки (как последовательности символов) в адекватное скрытое пространство с сохранением семантики. Это позволит решать задачу продолжения музыкальной последовательности и автоматического создания плавных «переходов» между разными фрагментами. Предлагается использовать VAE.
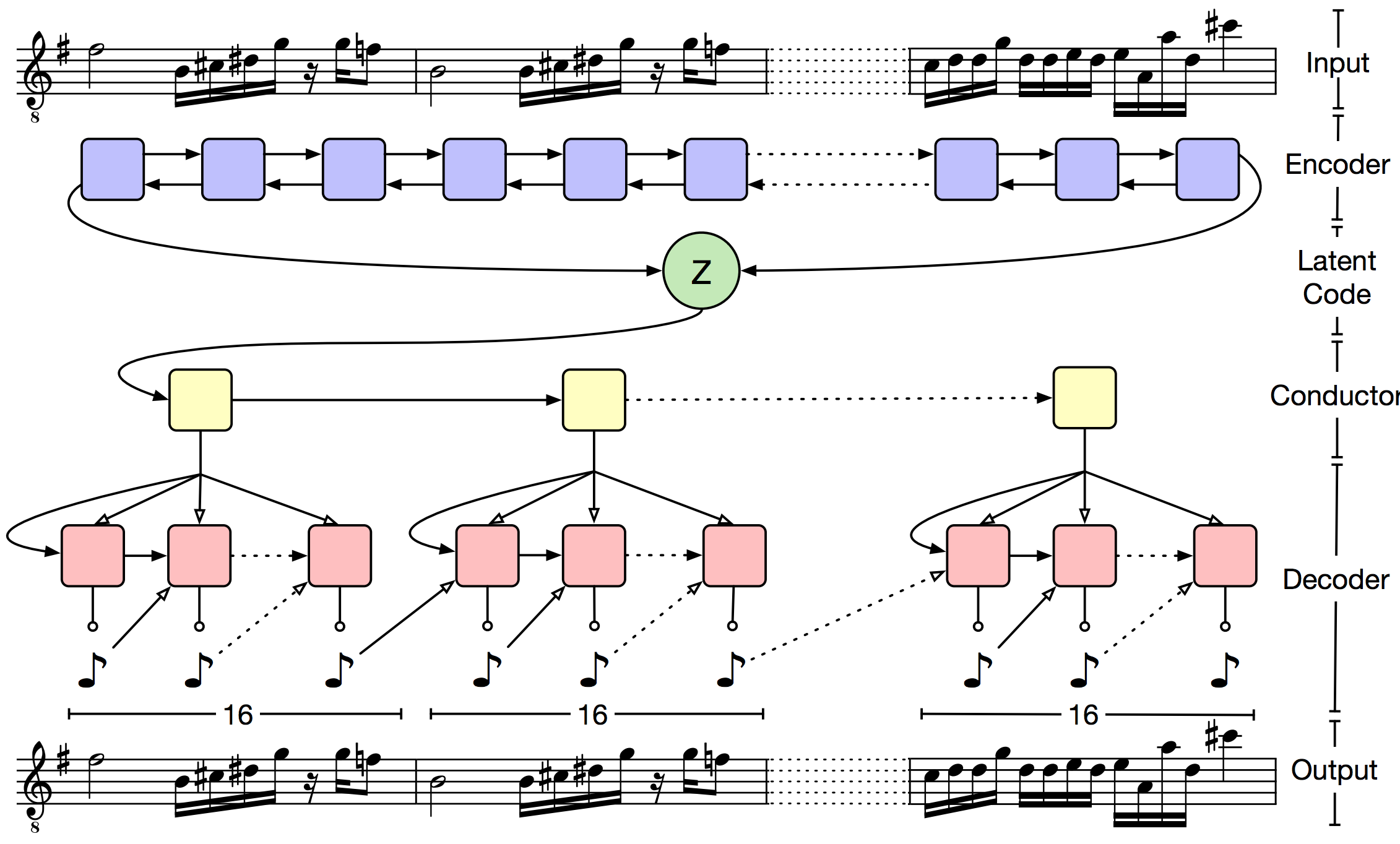
Основная проблема VAE состоит в том, что декодер очень быстро забывает «скрытый» код (latent code). Авторы предлагают бороться с этим через иерархический декодер. Выходная последовательность разбивается на небольшие кусочки (в статье музыку разбивали на такты). «Скрытый» код подается на вход верхнеуровневому декодеру, который возвращает эмбеддинг для такта. А затем LSTM нижнего уровня предсказывает ноты внутри такта. Формально такой подход не решает проблему забывания, но на практике оказывается, что полученные последовательности гораздо лучше соответствуют исходному кусочку.
Энкодер представляет собой bidirectional LSTM. Скрытые слои и конкатенируются и используются для предсказания параметров распределения :
Общая схема сети выглядит так:
Для оценки качества используется Lakh MIDI Dataset, в котором содержится примерно полтора миллиона midi-файлов. Авторы использовали только треки с размером 4/4. На коротких последовательностях (предсказание следующих двух тактов) качество MusicVAE сравнимо с классическим VAE. Однако уже на предсказании 16 тактов, доля ошибок классического VAE более 27%, а для иерархического метода в интервале 5-11%. Также показано, что иерархический метод дает более плавную интерполяцию между фрагментами музыки.
На закуску: над latent code векторами можно производить арифметические действия. Например, авторы построили вектора для 5 музыкальных характеристик (C diatonic membership, note density, average interval, 16th and 8th note syncopation). К сэмплируемым векторам можно с некоторыми весами прибавлять вектора характеристик, и итоговая последовательность, получаемая на выходе декодера, будет в зависимости от веса более или менее соответствовать заданной характеристике.
При обучении VAE важно выбрать правильную форму , поскольку от его выразительности зависит точность нижней оценки правдоподобия. Хорошее семейство должно удовлетворять следующим свойствам:
– Оно достаточно гибкое (в идеале – может аппроксимировать любое распределение).
– Из него можно быстро получать выборку.
– У полученной выборки легко посчитать правдоподобие.
– Сложность этих операций растет линейно с увеличением размерности.
Один из подходов к построению таких семейств — нормализующие потоки. Они основываются на формуле замены переменных: если случайную величину трансформировать с помощью обратимой дифференцируемой функции , плотность величины равна , где – якобиан функции . Выбрав семейство функций, у которых можно эффективно считать определитель якобиана, можно получать сложные распределения, трансформируя гауссовский шум.

В предыдущем подходе (Inverse Autoregressive Flow) каждый элемент вектора подвергается аффинному преобразованию, параметры которого задает авторегрессионная нейросеть (например, MADE или PixelCNN), смотрящая на предыдущие элементы , .
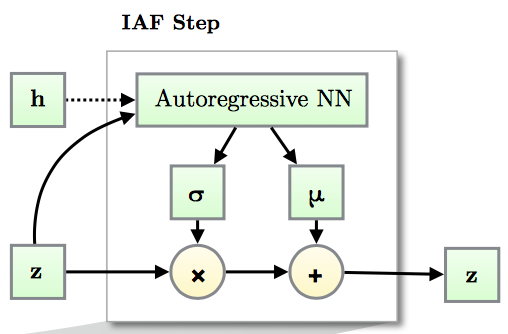
За счет авторегрессионной структуры сети, якобиан получающегося преобразования нижнетреугольный, а значит, его определитель легко посчитать как произведение диагональных элементов.
IAF – мощное семейство, но из-за того, что на каждом шаге используется аффинное преобразование, оно не способно хорошо аппроксимировать мультимодальные распределения.
Основные идеи авторов статьи
– Вместо аффинного преобразования в IAF использовать миниатюрную нейронную сеть с положительными весами и строго монотонными активациями.
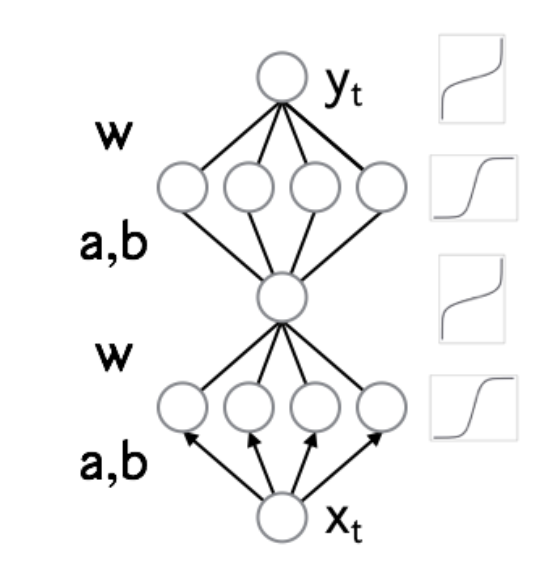
– Получившийся нормализующий поток является универсальным аппроксиматором для распределений.
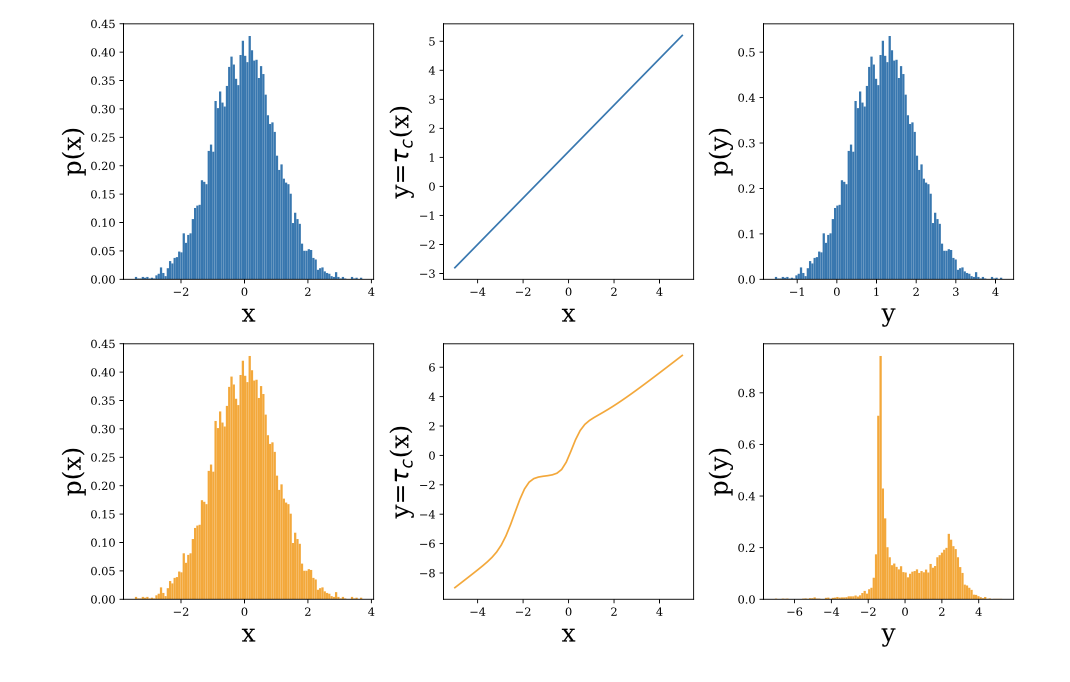
– Предложены две архитектуры трансформирующих сетей и описан механизм масштабирования на большие размерности с помощью conditional batch normalization.
– Эксперименты показывают, что NAF действительно может выучивать мультимодальные вещи.

Если одной фразой — это super-resolution без GAN'ов.
Классический подход к задаче super-resolution (получение чистой картинки из более зашумленной) заключается в том, чтобы на вход алгоритму подавать зашумленные изображения и учить предсказывать чистое изображение. Но что делать, если у нас нет чистых изображений? Это актуально для обработки фотографий с телескопов, снимков МРТ и других подобных задачах. Предложенная в статье идея – это учить сеть на зашумленных изображениях. Но нужно, чтобы шум на изображениях был в среднем нулевой. Авторы делают вывод: "...we can, in principle, corrupt the training targets of a neural network with zero-mean noise without changing what the network learns". На датасетах, которые они рассматривают, результаты не сильно хуже, а иногда и лучше, чем state of the art. К тому же скорость работы и скорость обучения намного выше.
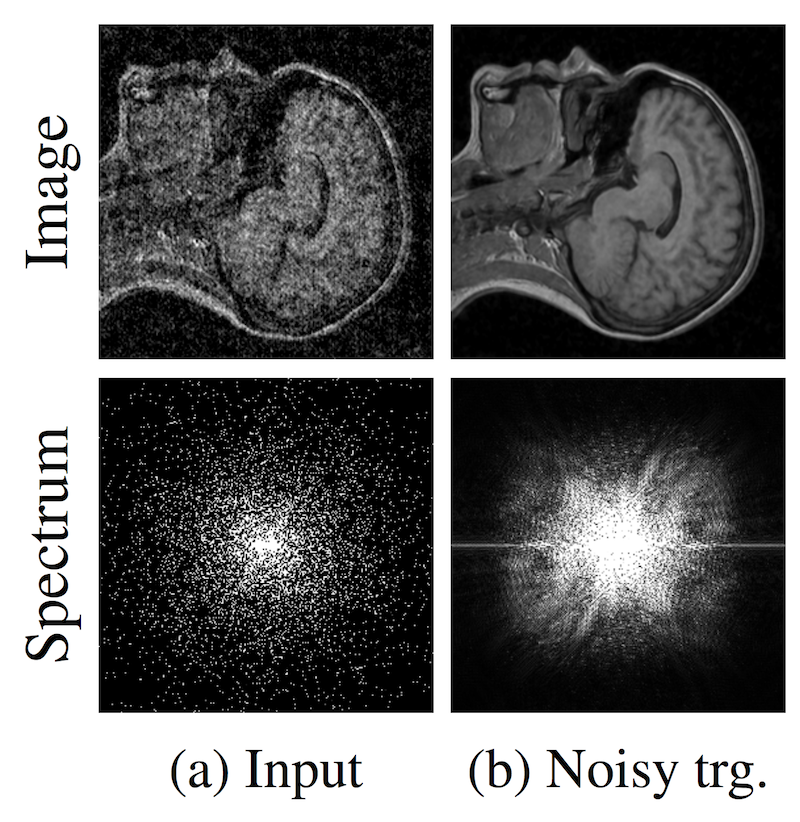
Авторы пробовали работать с кадрами из видео, однако, сделать super-resolution видео у них пока не очень получилось – восстановленное изображение «прыгает».
Несмотря на то, что ICML посвящена машинному обучению, на неи? можно встретить и много хороших докладов по смежным областям. Так, на секции, посвященнои? работе с распределенными вычислениями, был представлен интересныи? алгоритмическии? доклад по графам.
Допустим, мы хотим решить некоторую задачу на графе. Задача достаточно абстрактная, чтобы описать ее в терминах формальнои? логики. Например, нам дан граф связи пользователеи?, а мы хотим детектировать в нем аномалии (бот-сети, фрод) или выявить связи с сообществами людеи?.
Для этих и многих других задач при обучении моделеи?, связанных с графами, хорошо подои?дет выделение сущностеи?, называемых k-core.
Важно заметить, что интересует не только подход к извлечению этих k-core, но и возможность делать это эффективно, распределенно, а во возможности еще и на потоке. Именно такие реализации и были сразу же представлены в этом докладе.
Определения
Пусть – неориентированныи? граф с вершинами и ребрами, – подграф . Для каждои? вершины мы обозначим через степень этои? вершины, а для обозначим как – степени в подграфе .
-Core – максимальныи? подграф , такои? что для имеем , иными словами – степень любои? вершины не превосходит . Так же такои? граф называют называют -вырожденным.
Говорят, что вершина имеет coreness number , если она принадленжит -core, но не принадлежит -core.
Core labeling графа – граф, где каждая вершина помечена своим coreness number. Стоить отметить, что core labeling уникален и определяет иерархическое разложение .
Approximate -core – подграф в такои?, что .
На рисунке ниже примеры 3?core и -approximate 3-core.
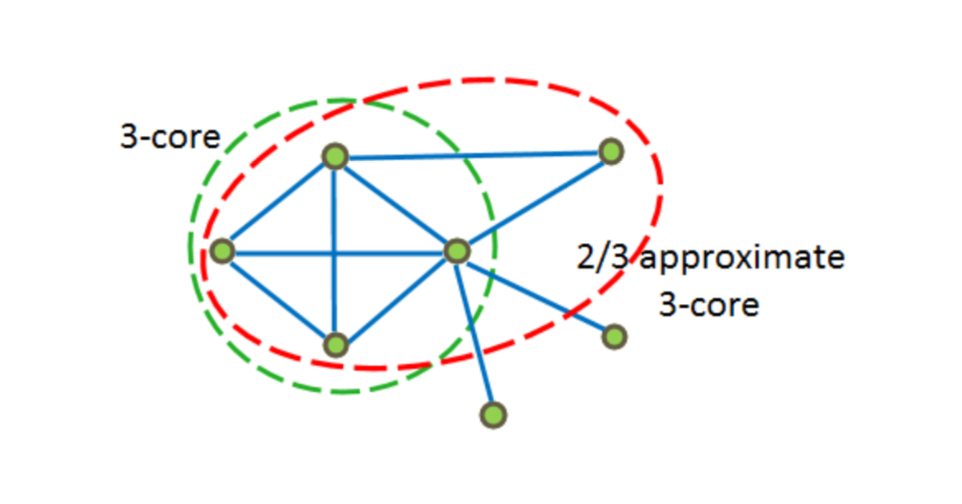
Идея алгоритма
Основная идея лежит в том, чтобы более уверенно выкидывать ребра в плотных областях и менее уверенно в разреженных.
Краткое описание алгоритма:
– выкидываем ребра из графа с вероятностью ;
– для каждои? вершины определяем ее coreness number, то есть делаем core labeling, находим максимальныи? -core, и добавляем все его вершины в множество ;
– удаляем из все ребра, оба конца которых находятся в ;
– проделываем все то же самое, увеличивая в два раза, пока возможно.
Псевдокод:

Разберем, как можно реализовать данныи? алгоритм в идеологии MapReduce для параллельных вычислении?.
Утверждается, что при стартовои? вероятности алгоритм выполняется не более итерации?. На первои? итерации путем выкидывания ребер мы получаем некоторыи? подграф . На второи? итерации на каждои? машине делаем core labeling . Сохраним вершины с наибольшим core number в некотором сете . На третьеи? итерации посылаем всем машинам сет и параллельно выкидываем из ребра, оба конца которых есть в , получаем . Далее с вероятностью проделываем то же самое раз.
Псевдокод:

Примечание
Вернемся к поиску сообществ на графе. Рассмотрим граф социальных связеи?. Например, граф, где вершины соответствуют пользовательским страницам в социальнои? сети, а ребра показывают, что пользователи добавили друг друга в друзья. Так же мы знаем о каком-то подмножестве страниц информацию о том, где данныи? пользователь учится (город, университет, факультет, специальность, группа).
В таком случае выявленную нами иерархию с -core можно интерпретировать следующим образом: ядра более высокого порядка отображают группу, в которои? учится студент, – сообщество достаточно узкое, но с высокои? плотностью связеи? в нем. Ядро порядка ниже отразит сообщество-специальность данного пользователя – связеи? в целом меньше, но они достаточно плотные. Двигаясь дальше по иерархии находим сообщества и факультета, и университета.
Эксплуатация даннои? идеи для спам аналитики выглядит менее явнои?, но похожа по сути. Если у нас есть представление, о том какие ядра считать хорошими, то использование факторов вроде «максимальныи? порядок -core, которому принадлежит пользователь», «плотность -core пользователя», а так же соотношение с ближаи?шими сущностями могут хорошо помогать при детектировании подозрительных узлов и выявлению паттерна бот-сетеи?.
Сегодня мы рассказали лишь о пяти докладах, но в рамках конференции ICML их было куда больше. Если специалистам в области машинного обучения будет интересен такой формат, то мы могли бы повторять его и в будущем.

Кстати, на фото выше шутка организаторов – это статистика по словам из писем тех, кто отправлял свой доклад на конференцию. Точнее, из писем с ответами на критику рецензентов, которые привели к приёму доклада. Тут же приведен «идеальный» ответ, с точки зрения машинного обучения. Но мы отвлеклись, переходим к обзору пяти лучших докладов (все заголовки кликабельны и ведут на работы докладчиков).
1. Fixing the broken ELBO
Один из самых интересных докладов про генеративные модели и обучение представлений на конференции.
Предыстория
Вариационные автокодировщики (VAE) пытаются моделировать распределение наблюдаемых данных следующим процессом:
1. Вначале из некоторого априорного распределения выбирают «скрытую» переменную .
2. Затем с помощью нейросети-декодера c параметрами из нее получают параметры распределения .
3. Из полученного распределения выбирают очередной объект.
Такая формулировка позволяет строить из простых кирпичиков весьма сложные модели и хорошо интерпретируемые представления. Например, если – это двумерное нормальное распределение, а – 724-мерный бернуллевский вектор, VAE удачно выучивает многообразие цифр MNIST.
Если в полученном пространстве на месте точек нарисовать матожидание соответствующих распределений , мы увидим, что модель аккуратно уложила многообразие цифр на плоскость.

А если для каждого класса цифр из тестового набора нарисовать апостериорное распределение отдельным цветом, мы увидим, что скрытые переменные выучивают очень полезные представления: на таких двухмерных признаках куда проще научить классификатор, и ему точно не понадобится много размеченных данных.

Правдоподобие наблюдаемых данных в такой модели записывается в виде:
Если задается глубокой нейросетью, у нас нет никаких шансов взять этот интеграл аналитически, поэтому прямая максимизация правдоподобия оказывается невозможной. Вместо этого используют так называемый вариационный байесовский вывод:
– Для каждого объекта обучающей выборки вводится вспомогательное распределение , описываемое параметром . Задача – как можно точнее аппроксимировать апостериорное распределение . Другими словами, оно предсказывает из каких был получен наблюдаемый объект .
– Записывается нижняя оценка на логарифм правдоподобия выборки:
Эта нижняя оценка также называется ELBO (Evidence Lower Bound) – нижняя граница обоснованности. Она в точности равна логарифму правдоподобия если .
– Полученная оценка максимизируется по и стохастическим градиентным спуском, при этом стохастический градиент внутреннего интеграла получается либо с помощью reparametrization trick, либо с помощью log-derivative trick (он же score function estimator, он же REINFORCE).
Поскольку хранить и оптимизировать параметры для каждого объекта выборки слишком дорого, вводится дополнительная нейросеть-энкодер, которая принимает на вход и возвращает . Такой подход называется амортизированным вариационным выводом. Именно использование амортизированного вывода позволило учить сложные иерархические вероятностные модели на больших данных.
Слишком умный декодер
Когда мы ограничиваем простым семейством распределений (например нормальными распределениями с диагональными матрицами ковариации), выучивает полезные представления данных. Простой арифметикой в пространстве можно менять прическу у человека на фотографии или смешивать мелодии.

Однако, простые модели, в которых все элементы вектора независимы при условии , не очень хорошо справляются со сложными данными, например с текстами или изображениями в высоком разрешении. Разумно пытаться использовать в качестве сложные «нейросетевые» распределения: авторегрессионные сети, такие как WaveNet или PixelCNN, нормализующие потоки, например, RealNVP, вложенные VAE, или даже -GAN.
При попытке обучить VAE с такими декодерами исследователи сталкиваются с большими трудностями: «слишком умный» декодер сам «съедает» всю энтропию в данных и вообще перестает смотреть на скрытую переменную. и оказываются независимыми, и получить полезные представления из скрытой переменной не получается. В разных статьях были предложены способы обойти эту проблему, но в основном они сводятся либо к упрощению декодера, либо к разным хакам при обучении. Авторы рассматриваемой статьи предлагают первое фундаментальное объяснение причин этого эффекта и способы борьбы с ним.
Главные идеи статьи
– Аппарат из Information Bottleneck Theory применяется к задаче обучения представлений. Авторы предлагают рассмотреть взаимную информацию между и . Когда взаимная информация равна , скрытая переменная сжимает данные без потерь: мы получаем идеальный автокодировщик. Когда взаимная информация равна нулю, скрытая переменная независима от данных, декодер «сожрал» всю энтропию. Для того чтобы обучить полезные представления, мы хотим получить вариант посередине: скрытая переменная должна описать важную информацию об объекте (например, форма лица, цвет глаз, ...) и выбросить детали (цвета конкретных пикселей, текстуры).
– Предлагается смотреть на VAE с альтернативной позиции: пусть теперь основная часть модели , а и – аппроксимации для и маржинального распределения .
– Для фиксированного рассматриваются нижняя и верхняя оценки на взаимную информацию, зависящие от и :
где – энтропия данных, – потери при сжатии и – KL-дивергенция между и

Каждому семейству моделей соответствует выпуклое множество точек в RD пространстве, форма этого множества зависит от «баланса сил» между энкодером и декодером.
– Показано, что оптимизация ELBO эквивалента минимизации , то есть поиску точки с коэффициентом касательной на границе множества. Если декодер достаточно гибкий и не в состоянии хорошо аппроксимировать , модели не выгодно вкладывать дополнительную информацию в латентную переменную: с точки зрения ELBO дешевле выучить ее декодером.
– Для построения наиболее полезных представлений, авторы предлагают оптимизировать , где – гиперпараметр, отвечающий за баланс между энкодером и декодером.
– Авторы экспериментально показали, что варьируя , можно выучивать представления с разным уровнем абстракции: от автоэнкодера (), который сжимает данные без потерь, до «автодекодера» (), который полностью игнорирует данные. Подобрав значение , можно получить «семантический энкодер», который кодирует только общую форму объекта, или «синтаксический энкодер», который способен восстановить мелкие детали. При этом все эксперименты проводились с супермощным авторегрессионным PixelCNN++ декодером, который до этого не удавалось применять в VAE.

2. A Hierarchical Latent Vector Model for Learning Long-Term Structure in Music
Авторы ставят перед собой задачу отображения музыки (как последовательности символов) в адекватное скрытое пространство с сохранением семантики. Это позволит решать задачу продолжения музыкальной последовательности и автоматического создания плавных «переходов» между разными фрагментами. Предлагается использовать VAE.
Основная проблема VAE состоит в том, что декодер очень быстро забывает «скрытый» код (latent code). Авторы предлагают бороться с этим через иерархический декодер. Выходная последовательность разбивается на небольшие кусочки (в статье музыку разбивали на такты). «Скрытый» код подается на вход верхнеуровневому декодеру, который возвращает эмбеддинг для такта. А затем LSTM нижнего уровня предсказывает ноты внутри такта. Формально такой подход не решает проблему забывания, но на практике оказывается, что полученные последовательности гораздо лучше соответствуют исходному кусочку.
Энкодер представляет собой bidirectional LSTM. Скрытые слои и конкатенируются и используются для предсказания параметров распределения :
Общая схема сети выглядит так:

Для оценки качества используется Lakh MIDI Dataset, в котором содержится примерно полтора миллиона midi-файлов. Авторы использовали только треки с размером 4/4. На коротких последовательностях (предсказание следующих двух тактов) качество MusicVAE сравнимо с классическим VAE. Однако уже на предсказании 16 тактов, доля ошибок классического VAE более 27%, а для иерархического метода в интервале 5-11%. Также показано, что иерархический метод дает более плавную интерполяцию между фрагментами музыки.
На закуску: над latent code векторами можно производить арифметические действия. Например, авторы построили вектора для 5 музыкальных характеристик (C diatonic membership, note density, average interval, 16th and 8th note syncopation). К сэмплируемым векторам можно с некоторыми весами прибавлять вектора характеристик, и итоговая последовательность, получаемая на выходе декодера, будет в зависимости от веса более или менее соответствовать заданной характеристике.
3. Neural Autoregressive Flows
При обучении VAE важно выбрать правильную форму , поскольку от его выразительности зависит точность нижней оценки правдоподобия. Хорошее семейство должно удовлетворять следующим свойствам:
– Оно достаточно гибкое (в идеале – может аппроксимировать любое распределение).
– Из него можно быстро получать выборку.
– У полученной выборки легко посчитать правдоподобие.
– Сложность этих операций растет линейно с увеличением размерности.
Один из подходов к построению таких семейств — нормализующие потоки. Они основываются на формуле замены переменных: если случайную величину трансформировать с помощью обратимой дифференцируемой функции , плотность величины равна , где – якобиан функции . Выбрав семейство функций, у которых можно эффективно считать определитель якобиана, можно получать сложные распределения, трансформируя гауссовский шум.

В предыдущем подходе (Inverse Autoregressive Flow) каждый элемент вектора подвергается аффинному преобразованию, параметры которого задает авторегрессионная нейросеть (например, MADE или PixelCNN), смотрящая на предыдущие элементы , .

За счет авторегрессионной структуры сети, якобиан получающегося преобразования нижнетреугольный, а значит, его определитель легко посчитать как произведение диагональных элементов.
IAF – мощное семейство, но из-за того, что на каждом шаге используется аффинное преобразование, оно не способно хорошо аппроксимировать мультимодальные распределения.
Основные идеи авторов статьи
– Вместо аффинного преобразования в IAF использовать миниатюрную нейронную сеть с положительными весами и строго монотонными активациями.

– Получившийся нормализующий поток является универсальным аппроксиматором для распределений.

– Предложены две архитектуры трансформирующих сетей и описан механизм масштабирования на большие размерности с помощью conditional batch normalization.
– Эксперименты показывают, что NAF действительно может выучивать мультимодальные вещи.

4. Noise2Noise: Learning Image Restoration without Clean Data
Если одной фразой — это super-resolution без GAN'ов.
Классический подход к задаче super-resolution (получение чистой картинки из более зашумленной) заключается в том, чтобы на вход алгоритму подавать зашумленные изображения и учить предсказывать чистое изображение. Но что делать, если у нас нет чистых изображений? Это актуально для обработки фотографий с телескопов, снимков МРТ и других подобных задачах. Предложенная в статье идея – это учить сеть на зашумленных изображениях. Но нужно, чтобы шум на изображениях был в среднем нулевой. Авторы делают вывод: "...we can, in principle, corrupt the training targets of a neural network with zero-mean noise without changing what the network learns". На датасетах, которые они рассматривают, результаты не сильно хуже, а иногда и лучше, чем state of the art. К тому же скорость работы и скорость обучения намного выше.

Авторы пробовали работать с кадрами из видео, однако, сделать super-resolution видео у них пока не очень получилось – восстановленное изображение «прыгает».
5. Approximate k-core graph decomposition
Несмотря на то, что ICML посвящена машинному обучению, на неи? можно встретить и много хороших докладов по смежным областям. Так, на секции, посвященнои? работе с распределенными вычислениями, был представлен интересныи? алгоритмическии? доклад по графам.
Допустим, мы хотим решить некоторую задачу на графе. Задача достаточно абстрактная, чтобы описать ее в терминах формальнои? логики. Например, нам дан граф связи пользователеи?, а мы хотим детектировать в нем аномалии (бот-сети, фрод) или выявить связи с сообществами людеи?.
Для этих и многих других задач при обучении моделеи?, связанных с графами, хорошо подои?дет выделение сущностеи?, называемых k-core.
Важно заметить, что интересует не только подход к извлечению этих k-core, но и возможность делать это эффективно, распределенно, а во возможности еще и на потоке. Именно такие реализации и были сразу же представлены в этом докладе.
Определения
Пусть – неориентированныи? граф с вершинами и ребрами, – подграф . Для каждои? вершины мы обозначим через степень этои? вершины, а для обозначим как – степени в подграфе .
-Core – максимальныи? подграф , такои? что для имеем , иными словами – степень любои? вершины не превосходит . Так же такои? граф называют называют -вырожденным.
Говорят, что вершина имеет coreness number , если она принадленжит -core, но не принадлежит -core.
Core labeling графа – граф, где каждая вершина помечена своим coreness number. Стоить отметить, что core labeling уникален и определяет иерархическое разложение .
Approximate -core – подграф в такои?, что .
На рисунке ниже примеры 3?core и -approximate 3-core.

Идея алгоритма
Основная идея лежит в том, чтобы более уверенно выкидывать ребра в плотных областях и менее уверенно в разреженных.
Краткое описание алгоритма:
– выкидываем ребра из графа с вероятностью ;
– для каждои? вершины определяем ее coreness number, то есть делаем core labeling, находим максимальныи? -core, и добавляем все его вершины в множество ;
– удаляем из все ребра, оба конца которых находятся в ;
– проделываем все то же самое, увеличивая в два раза, пока возможно.
Псевдокод:

Разберем, как можно реализовать данныи? алгоритм в идеологии MapReduce для параллельных вычислении?.
Утверждается, что при стартовои? вероятности алгоритм выполняется не более итерации?. На первои? итерации путем выкидывания ребер мы получаем некоторыи? подграф . На второи? итерации на каждои? машине делаем core labeling . Сохраним вершины с наибольшим core number в некотором сете . На третьеи? итерации посылаем всем машинам сет и параллельно выкидываем из ребра, оба конца которых есть в , получаем . Далее с вероятностью проделываем то же самое раз.
Псевдокод:

Примечание
Вернемся к поиску сообществ на графе. Рассмотрим граф социальных связеи?. Например, граф, где вершины соответствуют пользовательским страницам в социальнои? сети, а ребра показывают, что пользователи добавили друг друга в друзья. Так же мы знаем о каком-то подмножестве страниц информацию о том, где данныи? пользователь учится (город, университет, факультет, специальность, группа).
В таком случае выявленную нами иерархию с -core можно интерпретировать следующим образом: ядра более высокого порядка отображают группу, в которои? учится студент, – сообщество достаточно узкое, но с высокои? плотностью связеи? в нем. Ядро порядка ниже отразит сообщество-специальность данного пользователя – связеи? в целом меньше, но они достаточно плотные. Двигаясь дальше по иерархии находим сообщества и факультета, и университета.
Эксплуатация даннои? идеи для спам аналитики выглядит менее явнои?, но похожа по сути. Если у нас есть представление, о том какие ядра считать хорошими, то использование факторов вроде «максимальныи? порядок -core, которому принадлежит пользователь», «плотность -core пользователя», а так же соотношение с ближаи?шими сущностями могут хорошо помогать при детектировании подозрительных узлов и выявлению паттерна бот-сетеи?.
Вместо эпилога
Сегодня мы рассказали лишь о пяти докладах, но в рамках конференции ICML их было куда больше. Если специалистам в области машинного обучения будет интересен такой формат, то мы могли бы повторять его и в будущем.


masai
Спасибо! Да, формат интересен, было бы здорово увидеть продолжение. А то статей и докладов выходит много, что-то пропускаешь, бывает.