«1С:Предприятие» 8.3.14 будет содержать функциональность, позволяющую значительно сократить время решения систем линейных уравнений за счёт использования алгоритма, основанного на теории графов.
Он оптимизирован для использования на данных, имеющих разреженную структуру (то есть содержащие не более 10% ненулевых коэффициентов в уравнениях) и в среднем и в лучшем случаях демонстрирует асимптотику ?(n?log(n)?log(n)), где n — количество переменных, а в худшем (при заполненности системы ~100%) его асимптотика сопоставима с классическими алгоритмами ( ?(n3)). При этом на системах, имеющих ~105 неизвестных, алгоритм показывает ускорение в сотни раз по сравнению с реализованными в специализированных библиотеках линейной алгебры (например, superlu или lapack).

Важно: статья и описанный алгоритм требуют понимания линейной алгебры и теории графов на уровне первого курса университета.
Представление СЛАУ в виде графа
Рассмотрим простейшую разреженную систему линейных уравнений:

Внимание: система сгенерирована случайным образом и будет использоваться далее для демонстрации шагов работы алгоритма
При первом же взгляде на неё возникает ассоциация с другим математическим объектом — матрицей смежности графа. Так почему бы не преобразовать данные в списки смежности, сэкономив оперативную память в процессе выполнения и ускорив доступ к ненулевым коэффициентам?
Для этого нам достаточно транспонировать матрицу и установить инвариант “A[i][j]=z ? i-я переменная входит в j-е уравнение с коэффициентом z”, а после для всякого ненулевого A[i][j] построить соответствующее ребро из вершины i в вершину j.
Полученный граф будет выглядеть так:
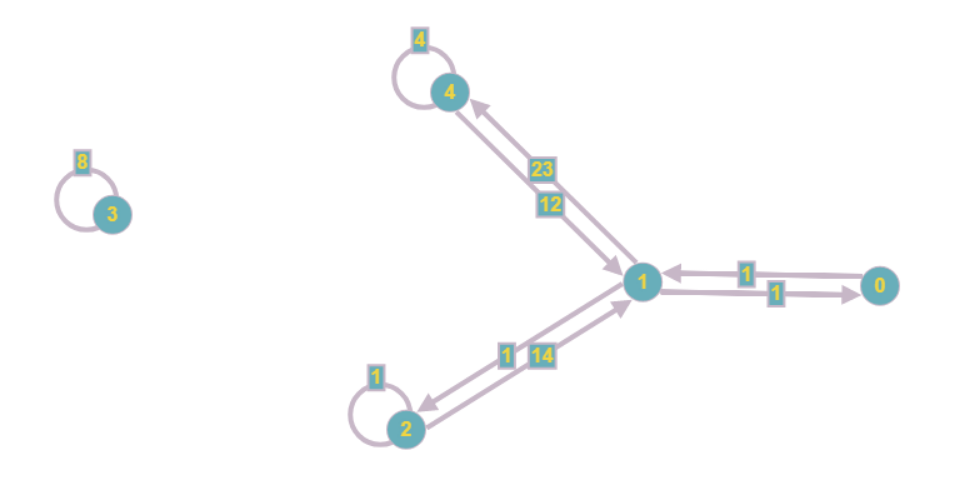
Даже визуально он оказывается менее громоздким, а асимптотические затраты оперативной памяти снижаются с O(n2) до O(n+m), где m — число коэффициентов в системе.
Выделение компонент слабой связности
Вторая алгоритмическая идея, которая приходит в голову при рассмотрении получившейся сущности: использование принципа “разделяй и властвуй”. В терминах графа это приводит к разделению множества вершин на компоненты слабой связности.
Напомню, компонента слабой связности — такое подмножество вершин, максимальное по включению, что между любыми двумя существует путь из рёбер в неориентированном графе. Неориентированный граф из исходного мы можем получить, например, добавлением к каждому ребру обратного (с последующим удалением). Тогда в одну компоненту связности будут входить все вершины, до которых мы можем дойти при обходе графа в глубину.
После разделения на компоненты слабой связности граф примет такой вид:
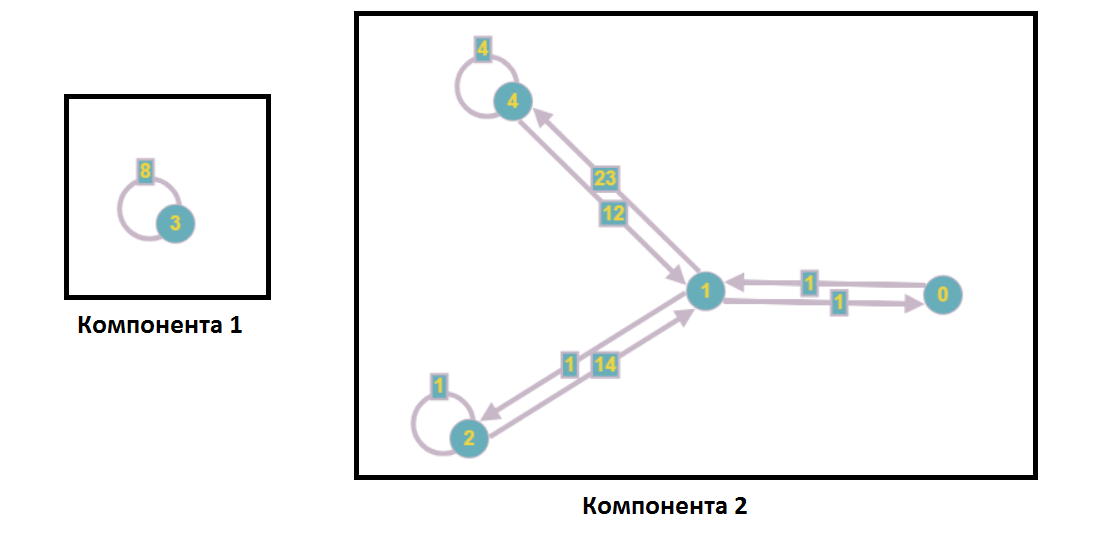
В рамках анализа системы линейных уравнений это значит, что ни одна вершина из первой компоненты не входит в уравнения с номерами второй компоненты и наоборот, то есть решать эти подсистемы мы можем независимо (например, параллельно).
Редуцирование вершин графа
Следующий шаг алгоритма — как раз то, в чём заключается оптимизация под работу с разреженными матрицами. Даже в графе из примера присутствуют “висячие” вершины, означающие, что в некоторые из уравнений входит всего одна неизвестная и, как мы знаем, значение этой неизвестной легко найти.
Чтобы определить такие уравнения, предлагается хранить массив списков, содержащих номера переменных, входящих в уравнение, имеющее номер этого элемента массива. Тогда, при достижении списком единичного размера, мы можем редуцировать ту самую “единственную” вершину, а полученное значение сообщить остальным уравнениям, в которые эта вершина входит.
Таким образом, вершину 3 из примера мы сможем редуцировать сразу, полностью обработав компоненту:
Аналогично поступим с уравнением 0, так как в него входит всего одна переменная:
Другие уравнения тоже изменятся после нахождения этого результата:
Граф принимает следующий вид:
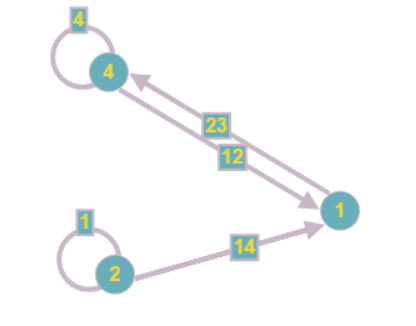
Заметим, что при редуцировании одной вершины могут возникнуть другие, тоже содержащие по одной неизвестной. Так что этот шаг алгоритма стоит повторять до тех пор, пока возможно редуцирование хотя бы одной из вершин.
Перестроение графа
Наиболее внимательные читатели могли заметить, что возможна ситуация, при которой каждая из вершин графа будет иметь степень вхождения не менее двух и продолжать последовательно редуцировать вершины будет невозможно.
Простейший пример такого графа: каждая вершина имеет степень вхождения, равную двум, ни одну из вершин нельзя редуцировать.
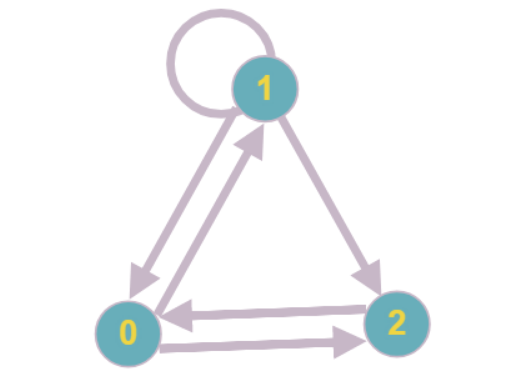
В рамках оптимизации под разреженные матрицы предполагается, что такие подграфы будут иметь малый размер, однако, работать с ними всё-таки придётся. Для расчёта значений неизвестных, входящих в подсистему уравнений, предлагается использовать классические методы решения СЛАУ (именно поэтому во введении указано, что при матрице, у которой все или почти все коэффициенты в уравнениях ненулевые, наш алгоритм будет иметь ту же асимптотическую сложность, что и стандартные).
Например, можно привести оставшееся после редуцирования множество вершин обратно в матричный вид и применить к нему метод Гаусса решения СЛАУ. Таким образом мы получим точное решение, а скорость работы алгоритма будет уменьшена за счёт обработки не всей системы, а лишь некоторой её части.
Тестирование алгоритма
Для тестирования программной реализации алгоритма мы взяли несколько реальных систем уравнений большого объёма, а также большое количество случайно сгенерированных систем.
Генерация случайной системы уравнений проходила через последовательное добавление рёбер произвольного веса между двумя случайными вершинами. Всего система заполнялась на 5-10%. Проверка корректности решений производилась через подстановку полученных ответов в исходную систему уравнений.

Системы имели размер от 1000 до 200000 неизвестных
Для сравнения быстродействия мы использовали наиболее популярные библиотеки для решения задач линейной алгебры, такие как superlu и lapack. Конечно, данные библиотеки ориентированы на решение широкого класса задач и решение СЛАУ в них никак не оптимизировано, поэтому различие в быстродействии оказалось значительным.
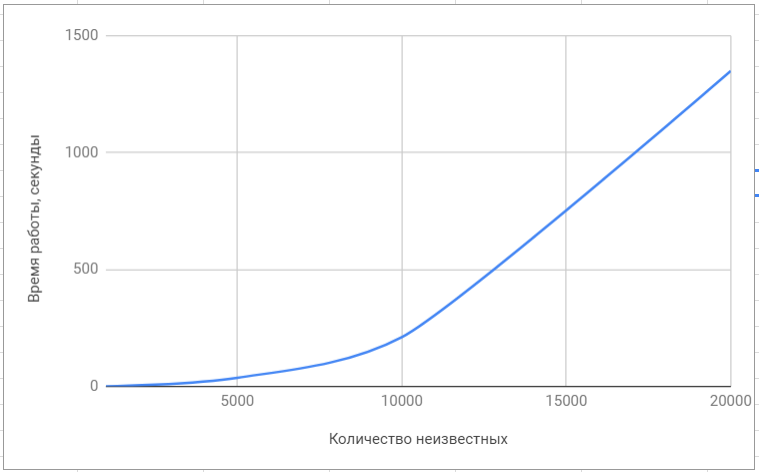
Тестирование библиотеки ‘lapack’
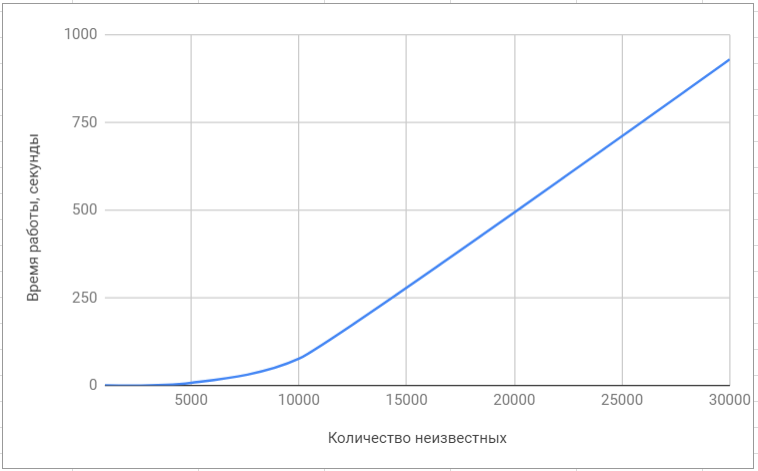
Тестирование библиотеки ‘superlu’
Приведём итоговое сравнение нашего алгоритма с алгоритмами, реализованными в популярных библиотеках:

Заключение
Даже если вы не являетесь разработчиком конфигураций «1С:Предприятие», идеи и методы оптимизации, описанные в данной статье, могут быть использованы вами не только при реализации алгоритма решения СЛАУ, но и для целого класса задач линейной алгебры, связанных с матрицами.
Для разработчиков же 1С добавим, что новая функциональность решения СЛАУ поддерживает параллельное использование вычислительных ресурсов, и можно регулировать количество используемых потоков вычисления.
Комментарии (51)

Taus
14.08.2018 12:57Какие версии superLU и LAPACK были в тесте? И какие конкретно алгоритмы решения СЛАУ в них были использованы?

PeterG Автор
14.08.2018 15:57superLU — v.5.1
lapack — v.3.8.0, использовался SGESV/SGESVX, потому что решались матрицы в общем виде (не обязательно симметричные и положительно определённые).
Библиотека использует алгоритм факторизации.
malkovsky
14.08.2018 17:08А у вас задача решить СЛАУ или найти LU факторизацию? Правда ли, что указанные солверы (supeLU, SGESV/SGESVX) делают LU факторизацию.
Вообще разреженные СЛАУ исследуют довольно давно, как минимум нужно иметь в виду упомянутые ранее в комментариях методы Крылова — для них базовая оценки не O(n^3), а O(nm), где m — количество ненулевых элементов (достигается кстати как раз в том числе за счет «списков смежности»). Уверен, Вы смогли бы ускориться за счет использования какой-нибудь разновидности метода Крылова после указанных графовых оптимизаций вместо Гаусса.
Пока что создается ощущение, что вы сравниваете «Гаусса» и «Гаусса + графовые оптимизации», и это ожидаемо, что в таком сравнении незаточенный под разреженность Гаусс будет медленней.
и в среднем и в лучшем случаях демонстрирует асимптотику ?(n?log(n)?log(n))
Откуда эта асимптотика была взята?
PeterG Автор
15.08.2018 08:431) Указанные солверы решают СЛАУ методом LU-факторизации (в частности superLU, lapack немного иначе раскладывает)
2)После графовых оптимизаций мы получаем плотные структуры, в которых применение метода Крылова не даст существенного выигрыша в асимптотике. Применение метода Крылова к исходному графу дало бы, как вы уже сказали, асимптотику в ?(nm), что, конечно, проигрывает нашей в общем случае
3) Вывод этой асимптотики — хорошая тема для отдельной большой статьи, но если вкратце — из произведения глубины орграфа, среднего количества рёбер, смежных с вершиной и n.
Andy_U
15.08.2018 13:00Интересно, вы пишите, что:
Вывод этой асимптотики —… — из произведения глубины орграфа, среднего количества рёбер, смежных с вершиной и n.
но в формуле я не вижу ни «глубины орграфа», ни «среднего количества рёбер, смежных с вершиной».
Далее, я не понимаю, как оценка ?(nm) (где m — некоторая константа) может оказаться хуже, чем ?(n?log(n)?log(n))?
PeterG Автор
15.08.2018 14:14m — не константа. А, вполне возможно, большое число. При коэффициенте заполнения 10% m=0.1*n^2
log(n) — средняя глубина орграфа при определенных допущениях. Так же log(n) — среднее число вершин, смежных с данной, при определенной структуре графа. Отсюда и оценка n*log(n)*log(n)
malkovsky
15.08.2018 14:34А почему среднее число вершин, смежных с данной — log(n)? У вас всего ребер ~ 0.1 * n^2, то средняя степень должна быть 2 * 0.1 * n.
Кроме того, ?(n?log(n)?log(n)) асимптотически меньше, чем n^2, а у вас количество ненулевых коэффициентов ~0.1 * n^2, получается, что Ваш алгоритм делает меньше операций, чем размер выходных данных.

dirkar
14.08.2018 13:40Вы бы для начала научились релизы без багов выпускать, а потом уже слау решали.
такое впечатление, что в 1с понятие тестирование продукта отсутствует полностью.
Neikist
14.08.2018 13:44Ну, справедливости ради, если сравнивать десктопную платформу с мобильной, а также с другими продуктами разных вендоров — количество багов вполне приемлимое.

Infactum
14.08.2018 14:00Только не надо смешивать в кучу платформу 1С: Предприятие и конкретные решения на этой платформе. У самой платформы все довольно-таки не плохо. Об этом даже предыдущая статья в их блоге была.

Anynickname
15.08.2018 00:00Есть мильён очевидных очень нужных и не делаемых годами вещей касаемо исключительно платформы (типа поддержки веб-клиентом хоть какого-нибудь браузера под Андроид), но нет, в очередной версии платформы мы внедряем «мегаполезную» функцию — решение СЛАУ.

EgorZanuda
15.08.2018 04:38+1Хорошо будем о платформе 8.3 от рождения как была глухой так и осталась. Когда пользователь пытается от крыть любой справочник, платформа постоянно переспрашивает вам точно открыть справочник? Такое ощущение что ты общаешься с глухим он тебя плохо слышит и постоянно уточняет или разработчики явно издеваются над пользователем.

acyp
15.08.2018 05:56или разработчики явно издеваются над пользователем
Я правильно Вас понял, что вы о работе в конфигурации в режиме пользователя? Если да, то о какой конфигурации идет речь? Только что ради любопытства открыл справочник контрагенты в БП (3.0.64.42), в рознице ((2.2.6.30, старенькая, но что нашлось на скорую руку) открыл «Склады» и «Номенклатура», ЗуП (3.1.6.6) — Сотрудники. Список я думаю можно продолжить, но уже результат — ни одного вопроса.
Второе:от крыть любой справочник, платформа постоянно переспрашивает
Не платформа, а конфигурация. Отсюда вопрос — Вы о какой конфигурации говорите? Можете указать Платформу, Конфигурацию и ее релиз? Конфигурация типовая или «дописанная»?
В целом, могу помочь разобраться «почему», но в этом ли была цель Вашего сообщения?

o4karek
15.08.2018 09:31В общем случае ваше утверждение абсолютно некорректно (мягко говоря).
Это проверяется примитивной конфигурацией, которую вы можете создать примерно за 30 секунд.
Хочется провозгласить стандартный лозунг — пруфы в студию!
В том смысле, что для начала хочется услышать полный номер версии платформы (включая разрядность), полное наименование используемой конфигурации (название, полный номер) и используемую ОС.
EgorZanuda
16.08.2018 04:32Платформа 8.3, управляемая форма на любой типовой конфигурации. К примеру создайте новый документ продажи или покупки попробуйте выбрать контрагента. По нажатию кнопки открыть форму выбора контрагента вам сначала откроется диалог выбора вариантов действий
Последние набранные
Введите строку поиска
Нажмите Показать все для выбора
Нажмите + (создать) для добавления
Вот собственно этот диалог и есть издевательство на пользователем. Зачем переспрашивать пользователя если он конкретно нажал кнопку Показать все?
И это не только на выборе контрагентов.
o4karek
16.08.2018 09:43Берем УТ 11.4.3. Открываем «Заказ клиента». Смотрим…
1. Поле «Контрагент» — в нем нет кнопки открытия формы выбора. А есть поле ввода (которое уже давно рекомендуется для ввода(!) имени) и есть кнопка «Выбрать из списка» (на ней треугольничек нарисован), по нажатию на которую открывается история ввода, где расположены 10 последних выборов оператора и возможность открыть форму выбора. При этом, если в поле «Контрагент» нажать кнопку F4 — сразу откроется форма выбора контрагента (но и история выбора останется доступной).
2. Справа от поля «Контрагент» находится поле «Склад». И вот там кнопка открытия формы выбора (на ней нарисовано ...) есть сразу. И ее нажатие открывает сразу форму выбора, без отображения истории ввода.
И это везде.
Платформа, в принципе, старается обеспечить максимально эффективную работу с документами/справочниками без использования мыши, только с клавиатуры. Практика показала, что подбор списка выбора при вводе текста — значительно эффективнее, чем копание в списках из тысяч и десятков тысяч элементов произвольной глубины вложенности.
Похоже, что вы не очень хотите изучать то, с чем приходится работать. Это печально :(
EgorZanuda
16.08.2018 11:32Платформа, в принципе, старается обеспечить максимально эффективную работу с документами/справочниками без использования мыши, только с клавиатуры.
Эффективность данного предложения очень сомнительная скорее отрицательная.
Двойной или тройной стук мышкой (даже если и клавиатурой сначала Tab потом F4) по одному реквизиту это уже не эффективно.
Новый документ — новая жизнь! Для чего эта история выпадающего списка из 10 последних? Из 100 новых документов максимум в 5 повторится контрагент причем в остальных 95 случаях в два раза больше придется выбирать нового контрагента, извините но это трата человеческого времени а не машины. Да и не каждый пользователь способен в голове держать массу команд от 1С.
Следующие пробуйте постоянно набирать тысячи разных позиций примерного наименования
ВНА-ПА-П-10/630-||-20зп УХЛ2
ПП53-16-1-149-1-УХЛ2
ПП53-25-1-045-1-УХЛ3
ОСК 10-20-Е05-3 УХЛ1
РЕ 19-45-31120 00 УХЛ3
Извините но у нас в стране не все только водкой и лицензиями для 1с торгуют.
Если пользователь попал мышкой с первого раза в треугольник, должен открыться справочник для выбора, а не пожелания от 1С.
o4karek
16.08.2018 11:57Эффективность данного предложения очень сомнительная скорее отрицательная.
Проф.операторы слышат такое утверждение с удивлением.
Для выбора нового контрагента стоит начать набирать его название. Ведь его выбирают не случайным числом, а потому, что он где указан (назван по телефону, в письме указан и т.д.)
если и клавиатурой сначала Tab потом F4
Для работы в нормально созданной форме, как правило, нужны следующие кнопки: ENTER, F4 и курсорные стрелки. Мышь нужна для выбора закладок и еще в ряде особых случаев. ENTER — великолепно обходит элементы.
Да и не каждый пользователь способен в голове держать массу команд от 1С.
Команд, которые необходимы каждый день — очень небольшой. И чтобы не запоминать — есть справка. А еще есть обучение использованию системой, где рассказывают, как пользоваться системой эффективно.
По вашему набору наименований достаточно набирать хотя-бы стартовые наименования компонентов, чтобы получать сокращенный перечень. При этом нет необходимости набирать все наименование — список адаптируется к набору. Т.е. набрав «пп53» я получу список из все переключателей, а набрав «пп53-16» — ограничу этот список переключателями на 16А. При этом можно указать, что в справочнике номенклатуры поиск при вводе будет идти не по началу строки (поведение по умолчанию), а по любому вхождению.
Также стоит помнить, что человек, долго занимающийся «своей» областью хорошо представляет себе правила формирования наименований и что они означают. Поэтому для такого человека преобразование фразы во фрагмент наименования происходит очень быстро.
Несмотря на все вышесказанное, я вполне допускаю, что предложенное поведение в используемом прикладном решении вас не устраивает. Ну так исправьте его! Для этого надо для нужных полей в документе(-ах) сделать «пару» кликов мышью и включить кнопку выбора вместо кнопки истории (а можно оставить и то и то).
Извините но у нас в стране не все только водкой и лицензиями для 1с торгуют.
Не может быть!
ЗЫ: Осталось только понять, как наша дискуссия относится к теме поста :)
EgorZanuda
17.08.2018 04:36Потому что Вы теоретики, а не практики.Это Ваша теория к сожалению на практике все намного сложнее.

moderndev
16.08.2018 12:22Затем, что это не кнопка «Показать все», а кнопка «Выбрать из списка», о чем свидетельствует иконка и контекстная подсказка. Кнопка выбора выглядит иначе: screenpresso.com/=qtSDc Также, если хочется открыть форму выбора сразу, можно нажать «F4» или правой кнопкой — «Выбрать». Лично мне и нашим пользователям такой подход, кажется логичным. Но ведь всем угодить невозможно, верно? :)

Dementor
17.08.2018 11:00Слова не специалиста, а обиженного пользователя.
(от куда вы вообще узнали такие умные слова как «платформе 8.3»?)
На практике в режиме конфигуратора для справочников выставляются настройки — «нужен ли список последних указанных в поле ввода элементов?», «можно ли разрешить создание новых элементов при вводе?». Далее разработчик прикладного решения сам решает какое поведение системы будет более удобным для пользователей его продукта.
Эффективность данного предложения очень сомнительная скорее отрицательная.
Двойной или тройной стук мышкой (даже если и клавиатурой сначала Tab потом F4) по одному реквизиту это уже не эффективно.
Новый документ — новая жизнь! Для чего эта история выпадающего списка из 10 последних?
Я поддерживаю старые конфигурации на обычных формах и меня иногда просят реализовать подобные «списки историй» — потому что это удобно и экономит людям время.

oleg-x2001
14.08.2018 15:07Приведенные выше графики были получены при решении систем на одном ядре? Если да, то как ваш алгоритм масшатбируется на большее число ядер? Я идеале, конечно, хотелось бы проверить полученные результаты (хотя код вы, наверно, в открытый доступ не выложите), а то как-то с трудом верится что ваша реализация работает намного быстрее superLU.

PeterG Автор
14.08.2018 15:56Приведенные выше графики были получены при решении систем на одном ядре?
Да, на одном.
Если да, то как ваш алгоритм масштабируется на большее число ядер?
В механизме предусмотрена возможность распараллеливания. Причём возможно как параллельное решение нескольких систем уравнений, так и распараллеливание решения каждой из систем. Использование вычислительных ресурсов можно настроить специальным свойством.
oleg-x2001
14.08.2018 16:13Даже для одного ядра ускорение по сравнению с superLU впечатляет (хотя, если честно, с трудом верится что это так на самом деле). Еще неплохо было бы сравнить с сольвером MUMPS. А вы можете привести графики ускорения расчета для нескольких ядер?

PeterG Автор
14.08.2018 16:38Графики в многопоточном режиме сейчас, к сожалению, сделать не сможем — это займет существенное время. К тому же сравнивать многопоточный режим для нашего механизма и сторонних библиотек может быть не вполне корректно, т.к. библиотеки могут работать с потоками по другому алгоритму, чем наш механизм.
Постараемся к релизу нашего механизма предоставить более полную информацию по быстродействию в многопоточном варианте.

Psychopompe
15.08.2018 09:33А где опубликован оригинал метода?

PeterG Автор
15.08.2018 10:23Нигде. Мы не реализовывали какой-либо чужой метод, а разработали свой.

Psychopompe
16.08.2018 12:36В таком случае другой вопрос: есть планы на публикацию?

PeterG Автор
17.08.2018 11:40Эта публикация как раз о том, как работает алгоритм. Какого-либо более расширенного поста не планируется, только пост про доказательство сложности работы.

kkonevets
15.08.2018 10:23К рисунку под фразой «Граф принимает следующий вид:»
А куда же делась вершина 0?
PeterG Автор
15.08.2018 10:24Вершина была редуцирована. Об этом говорится в посте, и приведённый рисунок как раз иллюстрирует это.

kkonevets
15.08.2018 10:41я извиняюсь, может я туплю, но как могла редуцироваться переменная x0, если редуцировались только x3, x1 и x2 к этому моменту? А x0 вообще равно 28 и про это ни слова.

PeterG Автор
15.08.2018 12:29как могла редуцироваться переменная x0
Цитата из статьи:
Аналогично поступим с уравнением 0, так как в него входит всего одна переменная

kkonevets
15.08.2018 12:40Так это написано про связь A[1][0], но связь A[0][1] то останется. Куда она делась?
По мне так ее нужно нарисовать стрелочкой от 0 к 1.

nadezhda_bb
15.08.2018 14:08так это не переменная x0 а уравнение 0, в которое входит одна переменная x1 она и редуцировалась!

kkonevets
15.08.2018 14:22ок, а как же переменная x0 в уравнении 1? куда делась она? на рисунке ее нет

nadezhda_bb
15.08.2018 14:33я тоже задаюсь этим вопросом ))) так как переменная x0 редуцироваться не может, это очевидно. Поэтому обратилась к PeterG в комментариях. Видимо где-то потеря произошла у автора )

kkonevets
15.08.2018 14:43ну да, там не сложно поправить, главное идея понятна

nadezhda_bb
15.08.2018 14:46ну может тогда поправить, раз указали на ошибку! идеи разные можно понаписать…

PeterG Автор
15.08.2018 17:16Переменная не редуцируется. Редуцировалось уравнение 0. Вершину с картинки убрали для явного понимания. Вообще должно исчезнуть одно ребро. Постараемся сделать картинку для иллюстрации.

kkonevets
15.08.2018 17:42нет!
вообще давайте забудем про слово «редуцируется», оно как-то уводит нас от смысла. А смысл в том что как раз должно остаться ребро к 0. А ребро от 0 должно исчезнуть. Вот и все.
PeterG Автор
16.08.2018 12:24Да, вы правы, удаление нулевой вершины — это следующий шаг, который был некорректно внесён на иллюстрацию. Схема должна выглядеть так(картинка прикреплена). Подразумевалось, что, зная значение х1, мы подставим его во все уравнения (таких у нас три, судя по рёбрам), и х0 сразу станет разрешим, тогда как для нахождения х2 и х4 потребуется ещё один шаг редукции.
Спасибо за внимательность.


kkonevets
15.08.2018 15:06В статье говорится что «шаг алгоритма стоит повторять до тех пор, пока возможно редуцирование хотя бы одной из вершин»
Поэтому вопрос — какова оценка сложности алгоритма с учетом этого цикла? Возможно ли что итеративное редуцирование приведет к долгой работе алгоритма?
Проблема в том что после того как мы редуцировали переменную мы подставляем ее в другие уравнения чтобы опять же редуцировать другие переменные. Насколько дешево это будет?
PeterG Автор
15.08.2018 17:17Подстановка как раз не сложная. Основная сложность алгоритма — в глубине редуцирования.
Думаю, сделаем еще одну статью с доказательством сложностей алгоритма, т.к. там много деталей и разных случаев. А то в комментариях есть большой риск потери нити рассуждений.
kkonevets
15.08.2018 17:38Я не имел ввиду что подстановка сложная. Да, именно глубина редуцирования.
Будем ждать.


Andy_U
Очень бы хотелось увидеть сравнение еще и с GMRES.
PeterG Автор
Вы имеете в виду реализацию GMRES в Матлабе?
Или в каком-то другом продукте?
Andy_U
Да где угодно, хоть в Python/scipy. Вот тут есть пример решения аж нелинейного интегро-дифференциального уравнения методом Крылова-Ньютона, где внутри именно что LGMRES. Оно решается при числе переменных 200x200 = 40000 на моем ультрабуке (i7-4500U) за 7 секунд. При размере сетки 400x400 = 160000 неизвестных, время решения 105 сек при включенной нелинейности и 80 сек при выключенной. И это при отсутствии прекондиционера.
Естественно, что нужно сравнивать на одних и тех же уравнениях и одном и том же компьютере…