Всем привет! В этой статье речь пойдет об одной важной части цифровой обработки сигналов — оконной фильтрации сигналов, в частности на ПЛИС. В статье будут показаны способы проектирования классических окон стандартной длины и «длинных» окон от 64K до 16M+ отсчетов. Основной язык разработки — VHDL, элементная база — современные кристаллы FPGA Xilinx последних семейств: это Ultrascale, Ultrascale+, 7-series. В статье будет показана реализация CORDIC — базового ядра для конфигурации оконных функций любой длительности, а также основных оконных функций. В статье рассмотрен метод проектирования с помощью языков высокого уровня С/C++ в Vivado HLS. Как обычно, в конце статьи вы найдете ссылку на исходные коды проекта.

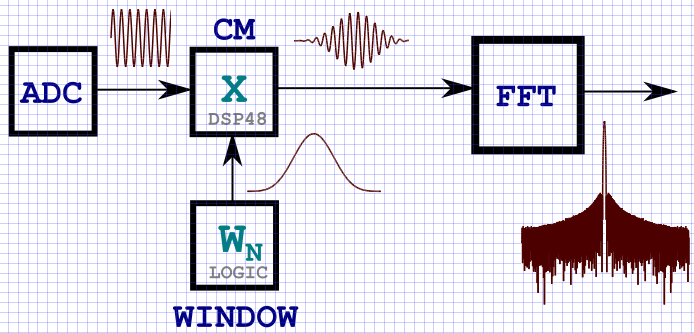
КДПВ: типичная схема прохождения сигнала через узлы ЦОС для задач анализа спектра.

Введение

Из курса «Цифровой обработки сигналов» многим известно, что для бесконечного по времени сигнала синусоидальной формы его спектр — это дельта-функция на частоте сигнала. На практике спектр реального ограниченного по времени гармонического сигнала эквивалентен функции ~sin(x)/x, а ширина главного лепестка зависит от длительности интервала анализа сигнала Т. Ограничение по времени есть ни что иное как умножение сигнала на прямоугольную огибающую. Из курса ЦОС известно, что умножение сигналов во временной области есть свертка их спектров в частотной (и наоборот), поэтому спектр ограниченного прямоугольной огибающей гармонического сигнала эквивалентен ~sinc(x). Это также связано с тем, что мы не можем интегрировать сигнал на бесконечном интервале времени, а преобразование Фурье в дискретной форме, выраженное через конечную сумму — ограничено по числу отсчетов. Как правило, длина БПФ в современных устройствах цифровой обработки на ПЛИС принимает значения NFFT от 8 до нескольких миллионов точек. Иными словами, спектр входного сигнала рассчитывается на интервале T, который во многих случаях равен NFFT. Ограничивая сигнал на интервале Т, мы тем самым накладываем «окно» прямоугольной формы, длительностью T отсчётов. Следовательно, результирующий спектр — есть спектр перемноженного гармонического сигнала и прямоугольной огибающей. В задачах ЦОС достаточно давно придуманы окна различной формы, которые при наложении на сигнал во временной области, позволяют улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Известная закономерность: чем сильнее подавление боковых лепестков, тем шире главный лепесток, и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Окна сложной формы рассчитываются путём взятия экспоненты (окно Гаусса) или модифицированной функции Бесселя (окно Кайзера), и в данной статье рассматриваться не будут. Более подробно об оконных функциях можно почитать в литературе, которую я по традиции приведу в конце статьи.

На следующем рисунке приведены типовые оконные функции и их спектральные характеристики, построенные с помощью средств САПР Matlab.

Реализация

В начале статьи я вставил КДПВ, которая показывает в общем виде структурную схему умножения входных данных на оконную функцию. Очевидно, что самый простой способ реализовать хранение оконной функции в ПЛИС — это записать её в память (блочную RAMB или распределенную Distributed — не имеет большого значения), а затем циклически извлекать данные в момент поступления входных отсчетов сигнала. Как правило, в современных ПЛИС объемы внутренней памяти позволяют хранить оконные функции относительно небольших размеров, которые затем перемножаются с поступающими входными сигналами. Под небольшими я понимаю оконные функции длиной до 64K отсчетов.

Но что делать, если длина оконной функции слишком большая? Например, 1М отсчётов. Нетрудно посчитать, что для такой оконной функции, представленной в 32-битной разрядной сетке потребуется NRAMB = 1024*1024*32/32768 = 1024 ячейки блочной памяти типа RAMB36K кристаллов FPGA Xilinx. А для 16М отсчетов? 16 тысяч ячеек памяти! Ни в одной современной ПЛИС столько памяти попросту нет. Для многих ПЛИС это слишком много, а в других случаях — это расточительное использование ресурсов ПЛИС (и, разумеется денежных средств заказчика).

В связи с этим нужно придумать метод генерации отсчетов оконной функции непосредственно в ПЛИС на лету, без записи коэффициентов с удаленного устройства в блочную память. К счастью, базовые вещи давно придуманы за нас. С помощью такого алгоритма, как CORDIC (метод "цифра за цифрой") удаётся проектировать множество оконных функций, формулы которых выражены через гармонические сигналы (Блэкмана-Харриса, Ханна, Хэмминга, Наттала и т.д.)

CORDIC

CORDIC — простой и удобный итерационный метод вычисления поворота системы координат, позволяющий вычислять сложные функции путём выполнения примитивных операций сложения и сдвига. С помощью алгоритма CORDIC можно вычислять значения гармонических сигналов sin(x), cos(x), находить фазу — atan(x) и atan2(x, y), гиперболических тригонометрических функций, поворачивать вектор, извлекать корень числа и т.д.

Сначала я хотел взять готовое ядро CORDIC и сократить объём работ, но к ядрам Xilinx у меня давняя нелюбовь. Поизучав репозитории на гитхабе, я понял, что все представленные ядра — не подходят по ряду причин (плохо документированы и нечитаемы, не универсальные, сделаны под конкретную задачу или элементную базу, написаны на verilog и т.д.). Затем я попросил товарища lazifo сделать эту работу за меня. С ней он конечно же справился, ведь реализация CORDIC — одна из простейших задач в области ЦОС. Но так как я нетерпелив, параллельно его работе я написал свой велосипед своё параметризируемое ядро. Основные особенности — конфигурируемая разрядность выходных сигналов DATA_WIDTH и входной нормированной фазы PHASE_WIDTH от -1 до 1, задание точности вычислений PRECISION. Ядро CORDIC выполнено по конвейерной параллельной схеме — на каждом такте ядро готово производить вычисления и принимать входные отсчеты. Ядро затрачивает на вычисление выходного отсчета N тактов, число которых зависит от разрядности выходных отсчетов (чем больше разрядность — тем больше итераций для вычисления выходного значения). Все вычисления происходят параллельно. Таким образом, CORDIC — базовое ядро для создания оконных функций.

Оконные функции

В рамках этой статьи я реализую только те оконные функции, которые выражены через гармонические сигналы (Ханна, Хемминга, Блэкмана-Харриса различного порядка и т.д). Что для этого нужно? В общем виде, формула для построения окна выглядит как ряд конечной длины.



Определенный набор коэффициентов a_k и членов ряда определяет название окна. Самое популярное и часто используемое — окно Блэкмана-Харриса: разного порядка (от 3 до 11). Ниже представлена таблица коэффициентов для окон Блэкмана-Харриса:



В принципе, набор окон Блэкмана-Харриса применим во многих задачах спектрального анализа, и нет нужды пытаться использовать сложные окна типа Гаусса или Кайзера. Окна Наттала или с плоской вершиной — это всего лишь разновидность окон с другими весовыми коэффициентами, но теми же базовыми принципами, что и Блэкмана-Харриса. Известно, что чем больше членов ряда — тем сильнее подавление уровня боковых лепестков (при условии разумного выбора разрядности оконной функции). Исходя из поставленной задачи, разработчику остается просто выбрать тип используемых окон.

Реализация на ПЛИС — традиционный подход

Все ядра оконных функций спроектированы с помощью классического подхода описания цифровых схем на ПЛИС и написаны на языке VHDL. Ниже представлен список сделанных компонентов:

• bh_win_7term — Блэкмана-Харриса 7 порядка, окно с максимальным подавлением боковых лепесков.
• bh_win_5term — Блэкмана-Харриса 5 порядка, включает в себя окно с плоской вершиной.
• bh_win_4term — Блэкмана-Харриса 4 порядка, включает в себя окно Наттала и Блэкмана-Наттала.
• bh_win_3term — Блэкмана-Харриса 3 порядка,
• hamming_win — окна Хемминга и Ханна.

Исходный код компонента окна Блэкмана-Харриса 3 порядка:

entity bh_win_3term is
	generic (
		TD          : time:=0.5ns;      --! Time delay
		PHI_WIDTH   : integer:=10;      --! Signal period = 2^PHI_WIDTH
		DAT_WIDTH   : integer:=16;      --! Output data width		
        XSERIES     : string:="ULTRA" --! for 6/7 series: "7SERIES"; for ULTRASCALE: "ULTRA";
	);
	port (
		RESET       : in  std_logic; --! Global reset 
		CLK         : in  std_logic; --! System clock 

		AA0         : in  std_logic_vector(DAT_WIDTH-1 downto 0); -- A0
		AA1         : in  std_logic_vector(DAT_WIDTH-1 downto 0); -- A1
		AA2         : in  std_logic_vector(DAT_WIDTH-1 downto 0); -- A2

		ENABLE      : in  std_logic; --! Clock enable
		DT_WIN      : out std_logic_vector(DAT_WIDTH-1 downto 0); --! Output	
		DT_VLD      : out std_logic --! Output data valid	
	);
end bh_win_3term;

В некоторых случаях я использовал библиотеку UNISIM для встраивания узлов DSP48E1 и DSP48E2 в проект, что в конечном счете позволяет увеличить скорость вычислений за счёт конвейеризации внутри этих блоков, но как показала практика — быстрее и проще дать волю лени и написать что-то типа P = A*B + C и указать в коде следующие директивы:

attribute USE_DSP of <signal_name>: signal is "YES";

Это отлично работает и жестко задает для синтезатора тип элемента, на котором реализуется математическая функция.

Vivado HLS

Кроме того, я реализовал все ядра с помощью средств Vivado HLS. Перечислю основные преимущества Vivado HLS — это высокая скорость проектирования (time-to-market) на языках высокого уровня С или С++, быстрое моделирование разрабатываемых узлов в связи с отсутствием понятия тактовой частоты, гибкая конфигурация решений (по ресурсам и производительности) путём внесения прагм и директив в проекте, а также низкий порог вхождения для разработчиков на языках высокого уровня. К главному недостатку можно отнести неоптимальные затраты ресурсов FPGA в сравнении с классическим подходом. Также не удается достичь тех скоростей работы, которые обеспечиваются классическими старыми RTL-методами (VHDL, Verilog, SV). Ну и самый большой недостаток — это танцы с бубном, но это свойственно всему САПР от Xilinx. (Прим.: в отладчике Vivado HLS и в реальной модели на С++ зачастую получались разные результаты, т.к. Vivado HLS криво работает при использовании преимуществ arbitrary precision).

На следующей картинке изображен лог синтезированного ядра CORDIC в Vivado HLS. Он достаточно информативен и отображает много полезной информации: количество используемых ресурсов, пользовательский интерфейс ядра, циклы и их свойства, задержку на вычисления, интервал вычисления выходного значения (важно при проектировании последовательных и параллельных схем):



Также можно посмотреть путь вычисления данных в различных компонентах (функциях). Видно, что на нулевом такте считываются данные фазы, а на 7 и 8 тактах выводится результат работы узла CORDIC.


Результат работы Vivado HLS: синтезированное RTL-ядро, созданное из C-кода. Лог показывает, что по временному анализу ядро успешно проходит все ограничения:



Еще один большой плюс Vivado HLS — для проверки полученного результата она сама делает тестбенч синтезированного RTL-кода на базе той модели, которая использовалась для проверки С-кода. Пусть это и примитивная проверка, но я считаю, что это очень круто и достаточно удобно позволяет сравнить работу алгоритма на С и на HDL. Ниже приведен скриншот из Vivado, показывающий симуляцию модели ядра оконной функции, полученного средствами Vivado HLS:



Таким образом, для всех оконных функций получились аналогичные результаты, независимо от метода проектирования — на VHDL или на C++. Однако, в первом случае достигается бОльшая частота работы и меньшее число используемых ресурсов, а во втором случае достигается максимальная скорость проектирования. Оба подхода имеют право на жизнь.

Я специально посчитал, сколько времени потрачу на разработку разными методами. Проект на C++ в Vivado HLS я реализовал в ~12 раз быстрее, чем на VHDL.

Сравнение подходов

Сравним исходные коды на HDL и С++ для ядра CORDIC. Алгоритм, как было сказано ранее, базируется на операциях сложения-вычитания и сдвига. На VHDL это выглядит следующим образом: имеется три вектора данных — один отвечает за поворот угла, а два других определяют длину вектора по осям X и Y, что эквивалентно sin и cos (см. картинку из вики):



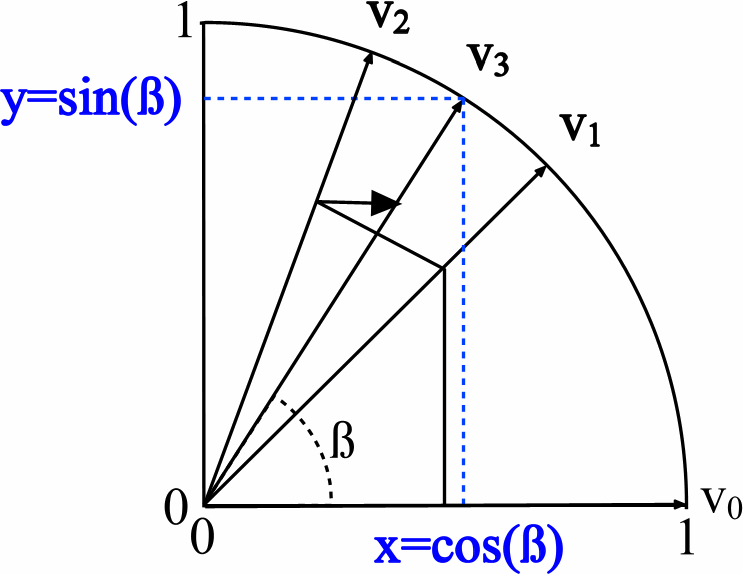
Путём итерационного вычисления значения Z, параллельно происходит вычисление значений X и Y. Процесс циклического поиска выходных значений на HDL:

constant ROM_LUT : rom_array := (
    x"400000000000", x"25C80A3B3BE6", x"13F670B6BDC7", x"0A2223A83BBB", 
    x"05161A861CB1", x"028BAFC2B209", x"0145EC3CB850", x"00A2F8AA23A9", 
    x"00517CA68DA2", x"0028BE5D7661", x"00145F300123", x"000A2F982950", 
    x"000517CC19C0", x"00028BE60D83", x"000145F306D6", x"0000A2F9836D", 
    x"0000517CC1B7", x"000028BE60DC", x"0000145F306E", x"00000A2F9837", 
    x"00000517CC1B", x"0000028BE60E", x"00000145F307", x"000000A2F983", 
    x"000000517CC2", x"00000028BE61", x"000000145F30", x"0000000A2F98", 
    x"0000000517CC", x"000000028BE6", x"0000000145F3", x"00000000A2FA", 
    x"00000000517D", x"0000000028BE", x"00000000145F", x"000000000A30", 
    x"000000000518", x"00000000028C", x"000000000146", x"0000000000A3", 
    x"000000000051", x"000000000029", x"000000000014", x"00000000000A", 
    x"000000000005", x"000000000003", x"000000000001", x"000000000000"
);

pr_crd: process(clk, reset)
begin
    if (reset = '1') then
        ---- Reset sine / cosine / angle vector ----
		sigX <= (others => (others => '0'));
		sigY <= (others => (others => '0'));
		sigZ <= (others => (others => '0'));
    elsif rising_edge(clk) then
		sigX(0) <= init_x;
		sigY(0) <= init_y; 
		sigZ(0) <= init_z;
		---- calculate sine & cosine ----
        lpXY: for ii in 0 to DATA_WIDTH-2 loop
            if (sigZ(ii)(sigZ(ii)'left) = '1') then
                sigX(ii+1) <= sigX(ii) + sigY(ii)(DATA_WIDTH+PRECISION-1 downto ii);
                sigY(ii+1) <= sigY(ii) - sigX(ii)(DATA_WIDTH+PRECISION-1 downto ii);
            else
                sigX(ii+1) <= sigX(ii) - sigY(ii)(DATA_WIDTH+PRECISION-1 downto ii);
                sigY(ii+1) <= sigY(ii) + sigX(ii)(DATA_WIDTH+PRECISION-1 downto ii);
            end if;
        end loop;
		---- calculate phase ----
        lpZ: for ii in 0 to DATA_WIDTH-2 loop
            if (sigZ(ii)(sigZ(ii)'left) = '1') then
                sigZ(ii+1) <= sigZ(ii) + ROM_TABLE(ii);
            else
                sigZ(ii+1) <= sigZ(ii) - ROM_TABLE(ii);
            end if;
        end loop;
    end if;
end process;

На языке С++ в Vivado HLS код выглядит практически аналогично, но запись в разы короче:

// Unrolled loop //
int k;
stg: for (k = 0; k < NWIDTH; k++) {
#pragma HLS UNROLL
	if (z[k] < 0) {
		x[k+1] = x[k] + (y[k] >> k);
		y[k+1] = y[k] - (x[k] >> k);

		z[k+1] = z[k] + lut_angle[k];
	} else {						
		x[k+1] = x[k] - (y[k] >> k);
		y[k+1] = y[k] + (x[k] >> k);

		z[k+1] = z[k] - lut_angle[k];
	}
} 	

Как видно, используется все тот же цикл со сдвигом и сложениями. Однако, по умолчанию все циклы в Vivado HLS «сворачиваются» и выполняются последовательно, как и задумано для языка С++. Введение прагмы HLS UNROLL или HLS PIPELINE преобразует последовательные вычисления к параллельным. Это приводит к увеличению затрачиваемых ресурсов ПЛИС, однако позволяет вычислять и подавать новые значения на ядро на каждом такте.

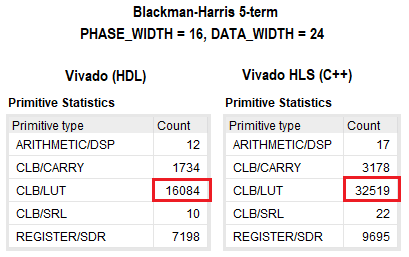
Результаты синтеза проекта на VHDL и C++ представлены на рисунке ниже. Как видно, по логике расхождение в два раза в пользу традиционного подхода. По остальным ресурсам ПЛИС расхождение незначительное. Я не сильно вдавался в оптимизацию проекта на С++, но однозначно путём задания различных директив или частичного изменения кода, количество используемых ресурсов можно сократить. В обоих случаях тайминги сошлись для заданной частоты работы ядра ~350МГц.

Особенности реализации

Поскольку вычисления производятся в формате с фиксированной точкой, то оконные функции имеют ряд особенностей, которые необходимо учитывать при проектировании систем ЦОС на ПЛИС. Например, чем больше разрядность данных оконной функции — тем лучше точность наложения окна. С другой стороны, при недостаточной разрядности оконной функции в результирующую форму сигнала будут внесены искажения, что отразится на качестве спектральных характеристик. Например, оконная функция должна иметь не менее 20 разрядов при умножении на сигнал длительностью 2^20 = 1M отсчётов.

Заключение

В данной статье показан один из способов проектирования оконных функций без использования внешней памяти или блочной памяти FPGA. Приведен метод задействования исключительно логических ресурсов ПЛИС (и в некоторых случаях DSP-блоков). Используя алгоритм CORDIC, удается получать оконные функции любой разрядности (в рамках разумного), любой длины и порядка, а следовательно — иметь набор практически любых спектральных характеристик окна.

В рамках одной из работ мне удалось получить стабильно работающее ядро оконной функции Блэкмана-Харриса 5 и 7 порядка на 1М отсчетов на частоте ~375МГц, а также сделать генератор поворачивающих коэффициентов для БПФ на базе CORDIC на частоте ~400МГц. Используемый кристалл ПЛИС: Kintex Ultrascale+ (xcku11p-ffva1156-2-e).

Ссылка на проект github здесь. В проекте содержится математическая модель в Matlab, исходные коды оконных функций и CORDIC на VHDL, а также модели перечисленных оконных функций на C++ для Vivado HLS.

Полезные статьи

• Оконные функции DSPLib
• Некоторые оконные функции DSPlib
• Развернутая статья на Wiki по оконной фильтрации
• Статья на Wiki про CORDIC
• Vivado HLS Userguide
• Статья про спектральный анализ на хабре

Также советую очень популярную книгу по ЦОС — Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход

Спасибо за внимание!