Волей случая в моих руках оказалась «все режимная покомпонентная модель авиационного двигателя» от солидного разработчика Центрального Института Авиационного Моторостроения (ЦИАМ), и конечно захотелось на ней испытать все эти регуляторы, которые рассматриваются на простых или упрощенных моделях агрегата. По своему образованию я конструктор ядерных реакторов, и про авиадвигатель, знаю только то, что он может упасть на защитную оболочку реактора вместе с самолетом и она должна выдержать. Прежде чем мучать настоящую модель, потренируемся на кошечках, до перехода на турбореактивные помучаем просту модель газотурбинного.

В этой статье мы создадим модель регулятора на базе стандартной библиотеки структурного моделирования (без использования готовой библиотеки блоков нечёткого регулирования).
В качестве объекта управления будет использована модель газотурбинного двигателя из учебника В.И. Гостева «Нечеткие регуляторы в системах автоматического управления»
Выполним сравнение с ПИД и ПДД регуляторами.

И уже в качестве наглядной демонстрации в следующей статье будем регулировать не упрощенную, а настоящую модель настоящего двигателя, которую использует ЦИАМ им. Баранова.

Постановка задачи

Отличие газотурбинного двигателя (ГТД) от турбореактивного (ТРД) в том, что у ГТД вся энергия снимается через вал. В ТРД энергия выделяемся в виде реактивной струи.

Газотурбинные двигатели (ГТД) широко применяются в газовой и авиационной промышленности, где являются основой газоперекачивающих агрегатов и авиационных силовых установок, в приводах промышленных электро-турбогенераторов пиковых и передвижных электростанций, в судовых энергетических установках и на других промышленных объектах, где требуется развитие больших единичных мощностей (от 1 до 25 МВт) в одном агрегате при его минимальной массе и габаритах.

К газотурбинным двигателям предъявляется комплекс требований, связанных с их надежностью, энергетической эффективностью, безопасностью и экологичностью в процессе эксплуатации. Наряду с этими требованиями, актуальными являются требования к качеству переходных процессов, связанных с запуском агрегата, резким изменением отбираемой нагрузки (мощности). Во многом удовлетворение этих требований возлагается на системы автоматического управления (САУ) ГТД.

Типовым ГТД, находящим применение в промышленности, является турбовальный двигатель, схема которого представлена на рисунке 1.

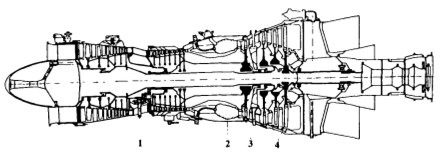
Рисунок 1. Схема типового промышленного ГТД:
1- компрессор; 2 — камера сгорания; 3 – турбина компрессора; 4 – силовая турбина.

Двигатель представляет собой роторную машину, в которой в компрессоре 1 происходит сжатие воздуха, в камере сгорания 2 осуществляется процесс горения топлива, подводимого к воздух, в турбине компрессора 3 часть энергии отбирается от горячих газов, расходуясь на привод компрессора 1, в силовой турбине 4 газы расширяясь создают мощность отбираемую от двигателя потребителем.

В подавляющем большинстве ГТД частота вращения ротора является управляемой величиной. В качестве управляющего фактора в САУ частотой вращения ротора n используется расход топлива Gт в камеру сгорания. На разных режимах работы и при различных внешних условиях параметры двигателя существенно изменяются.

Рассмотрим газотурбинный двигатель (ГТД) как нестационарный объект управления, для которого частота вращения ротора – n управляемая переменная, а расход топлива G_Т – управляющее воздействие. Линеаризуя зависимости момента турбины — М_Т и момента компрессора — М_К, от частоты вращения ротора и не учитывая влияние тепловой и массовой емкости двигателя для конкретного режима работы записывают передаточную функцию двигателя следующим образом:

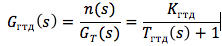
где коэффициент усиления и постоянная времени определяются как:

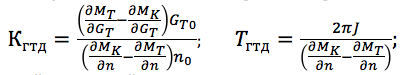
причем, входной и выходной сигналы записываются в относительных безразмерных отклонениях от установившегося режима (n = ?n/n₀; G_Т = ?G/G_TO, где базовые значения параметров выбраны для определенного режима работы двигателя, например, номинального или максимального). На разных режимах работы и при различных внешних условиях коэффициент усиления и постоянная времени двигателя существенно изменяются, поэтому для каждого режима необходимо определять свои значения K_ГТД и T_ГТД.

Заметим, что передаточная функция G _гтд (s) для нестационарного объекта управления, каким является газотурбинный двигатель, получена методом «замороженных» коэффициентов при условии достаточно медленного изменения параметров объекта.

Структурная схема аналоговой электромеханической системы автоматического управления частотой вращения ротора двигателя приведена на рисунке 2

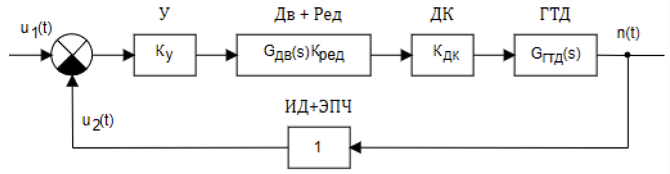
Рисунок 2. Структурная схема аналоговой САР ГТД

Частота вращения задается напряжением u₁(t) и изменяется импульсным датчиком ИД, частота выходного сигнала которого определяется выражением:

f = kmn, где n – число оборотов двигателя, m – число зубьев редуктора, k – коэффициент передачи. Переменное напряжение, снимаемое с выхода ИД с помощью электронного преобразователя частоты ЭПЧ, преобразуется в сигнал u2(t), величина которого пропорциональна числу оборотов двигателя — n. Напряжение u2(t) сравнивается с задающим напряжением и сигнал ошибки после усилителя У поступает на двухфазный асинхронный двигатель Дв, который через редуктор Ред регулирует дроссельный клапан ДК, изменяя расход топлива, поступающего в газотурбинный двигатель. Импульсный датчик вместе с электронным преобразователем частоты можно описать пропорциональным звеном с передаточной функцией, равной единице. При этом сама система имеет единичную обратную связь.

Рассматривая последовательное соединение усилителя, асинхронного двигателя, дроссельного клапана, газотурбинного агрегата и частотного датчика с электронным преобразователем частоты в качестве общего объекта управления, и применяя цифровой нечеткий регулятор, всю структурную схему с рисунка 2 можно привести к структурной схеме на рисунке 3. При этом все передаточные функции звеньев сводятся к общей передаточной функции G₀(s).

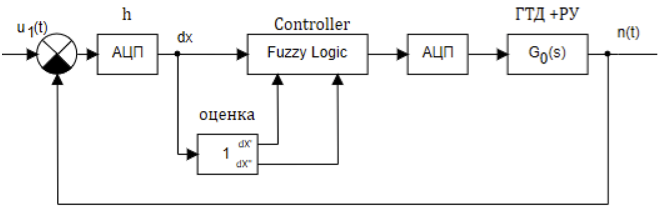
Рисунок 3. Структура системы управления с нечетким регулятором.

Общую передаточную функцию G0(s) можно записать в виде:

G₀(s) = К_УG_ДВ(s)K_РЕДК_ДКG_ГТД(s) = ?[s(s+a)(s+b)]^-1, где

? = abК_УK_ДВK_РЕДК_ДКK_ГТД,

а = 1/T_ДВ,

b =1/T_ГТД

Для примера принимаем, что зависимости передаточной функции от времени работы принимают следующие значения:

T_ГТД (t) = 0,9849 – 0,1188 ? t + 0,0063 ? t² – 0,00012 ? t³ ;

? (t) = 16,5475 – 4,4469 ? t + 0,4843 ? t² – 0,02315? t³ + 0,0004? t⁴;

T_ДВ = 0,35 c.

При исследовании системы управления предположим, что заданная функция изменения частоты вращения ротора газотурбинного двигателя задается входным напряжением u(t)

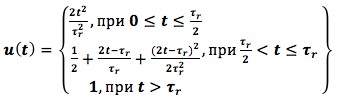
где ?_r – время разгона двигателя. Принимаем ?_r = 6 сек.

Создание динамической модели

Упрощенная модель двигателя представлена на рисунке 4. В данной модели мы используем переменные параметры типовых блоков, которые меняются в процессе моделирования зависимости, приведенной выше.

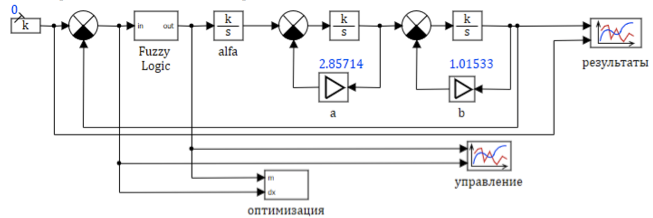
Рисунок 4. Структурная схема модели ГТД

Коэффициенты alfa, а, b усилителей рассчитываются с помощью скриптового языка, текст программы ниже:

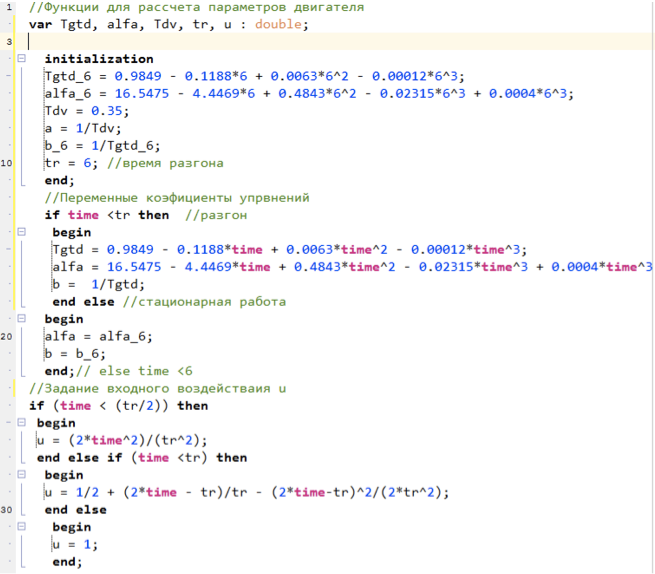
Рисунок 5. Скрипт расчета параметров модели.

Регулятор управления на базе нечеткой логики

Регулятор управления забирает на вход рассогласование между заданным значением и значением, полученным из модели, и должен вычислить управляющее воздействие.

Попробуем собрать регулятор на базе нечеткой логики, используя только стандартные математически блоки структурного моделирования, без использования специализированной библиотеки.

Описание принципов управления на базе нечеткой логики можно найти в предыдущей статье на хабре, либо в описании создания специализированной библиотеки блоков здесь (осторожно ненормативная лексика).

Любой регулятор на базе нечёткой логики выполняет следующую последовательность преобразований:

1. Фазификация входных переменных. Значение переменной заменяется набором термов.
2. Активизация заключений правил нечеткой логики.
3. Аккумуляция заключений для каждой лингвистической переменной.
4. Дефазификация выходных переменных.

Для управления двигателем будем использовать три непрерывные переменные, которые рассчитываются на основании одного сигнала:

1. отклонение;
2. производная отклонения (скорость изменения отклонение);
3. вторая производная отклонения (ускорение изменений отклонений).

Схема расчета представлена на рисунке 6:

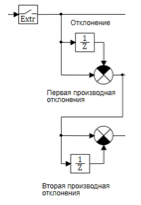
Рисунок 6. Вычисления первой и второй производной отклонения.

Блок-экстраполятор производит квантование сигнала, входящего в контроллер с периодом 0.01 сек. Первая и вторая производная вычисляется по разностным формулам:

где:

u(t) – текущее значение отклонения в момент времени t;

u(t-?t) – значение отклонения в момент времени t – ?t;

u’(t) – текущее значение производной отклонения в момент времени t;

u’(t-?t) – значение производной отклонения в момент времени t – ?t;

u’’(t) – текущее значение второй производной отклонения в момент времени t;

u’’(t-?t) – значение второй производной отклонения в момент времени t – ?t;

?t – период квантования.

Деление на ?t осуществляется в блоке сравнения.

В результате работы данного блока создаются три лингвистические переменные: отклонение, первая переменная отклонения, вторая переменная отклонения.

Для решения задачи нечеткого управления будем использовать для каждой лингвистической переменной только два терма.

Отклонение — меньше, больше;

Первая производная отклонения – уменьшается, увеличивается;

Вторая производная отклонения – замедляется, ускоряется.

Для вычисления значения функции принадлежности ? для каждого терма используем линейную функцию с насыщением. Данная функция для терма больше равна 0, когда входное значение минимально и 1 когда входное значение максимально. Для терма меньше данная функция принимает значение 1, когда переменная равна минимуму, и 0, когда переменная максимальна. (см. рис. 7)

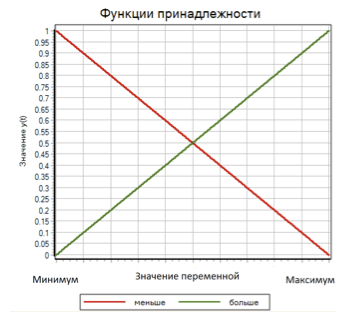
Рисунок 7. Функции принадлежности для термов меньше и больше.

Таким образом, для каждой из трех входных переменных (отклонение, 1-я производная отклонения, 2-я производная отклонения) появляются два терма больше и меньше, значение функций принадлежности ?_i у которых линейно меняются от 0, до 1 в зависимости от значения входной переменной.

В качестве выходной лингвистической переменной используем выходное воздействие у которого тоже только два терма уменьшать и увеличивать.

Из схемы модели рис. 4 очевидно, что если отклонение меньше 0, то значение больше заданного и нужно уменьшать. Если отклонение больше 0, то функция меньше заданной и нужно увеличивать.

Логические правила для двух термов будут выглядеть так:

• Если меньше и уменьшается и замедляется => уменьшать.
  
• Если больше и увеличивается и ускоряемся => увеличивать.

Для активизации правил нечеткого вывода используем функцию минимум для оператора нечеткого и. Значение функций принадлежности для термов выходной функции рассчитываются по формулам:

? _{уменьшать} = MIN (? _меньше, ? _{уменьшается}, ? _{замедляется})
? _{увеличивать} = MIN (? _больше, ? _{увеличивается}, ? _{ускоряется})

Для обеспечения пересчета термов в конкретные значения воздействия (аккумуляция и денацификация) используем алгоритм Цукамото (Tsukamoto), как центр тяжести точек.

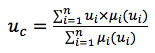где,
u_c – результирующая функция;
u_i – значение функции для терма i;
?_i– значение функции принадлежности для термов для функции.
В нашем случае результирующая функция для двух термов рассчитывается по формуле:

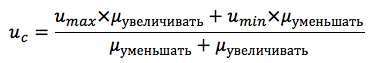
Общая схема алгоритма нечеткого вывода представлена на рисунке 8:

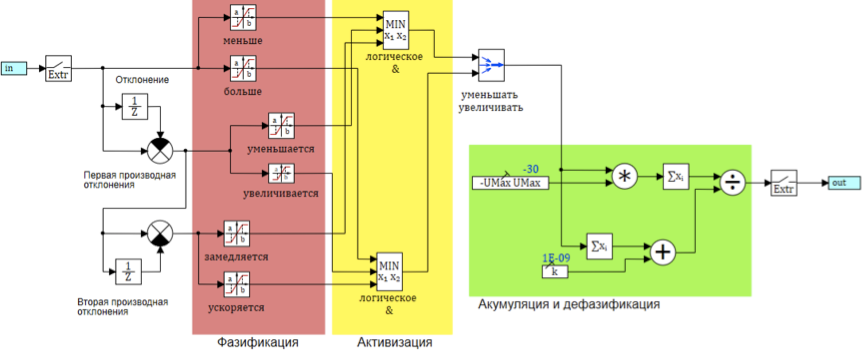
Рисунок 8. Схема алгоритма нечеткого вывода

Чтобы данный алгоритм заработал, мы должны задать минимальные и максимальные значения для 6 термов трех лингвистических переменных (отклонение, 1-я производная отклонения, 2-я производная отклонения). Для сокращения вычислений принимаем, что отклонение симметрично относительно нуля. Тогда нам достаточно найти 3 абсолютных значения, по одному для каждой переменной.

deltMaх – максимальное отклонение. Задает значения термов меньше, больше (-deltMaх, deltaMax);

divMaх – максимальная производная отклонения. Задает значения термов уменьшается, увеличивается (-divMaх, divMax);

div2Maх – максимальная вторая производная. Задает значения термов замедляется, ускоряется (-div2Maх, div2Max).

Максимальное и минимальное воздействие umin и umax определяются конструктивными особенностями и в данном примере принимаются равными +30 и -30.

Настройка регулятора оптимизацией.

Для подбора коэффициентов воспользуемся той же самой схемой оптимизации, которую мы применяли в предыдущих опытах с нечеткой логикой.

В качестве критериев оптимизации берем среднеквадратичное отклонение не более 0.001 и количество переключений в блоке управления не более 25. За переключение принимаем смену знака управляющего воздействия.

Схема блока настройки регулятора представлена на рис. 9.

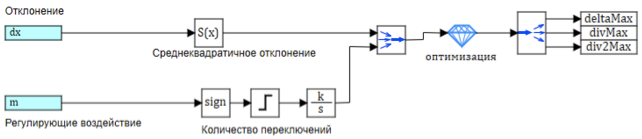
Рисунок 9. Настройка параметров нечеткого вывода.

В результате работы блока получены следующие параметры
deltMaх = 0.00746;
divMaх = 0.2657;
div2Maх = 25.13;

Результаты переходного процесса представлены рисунке 10

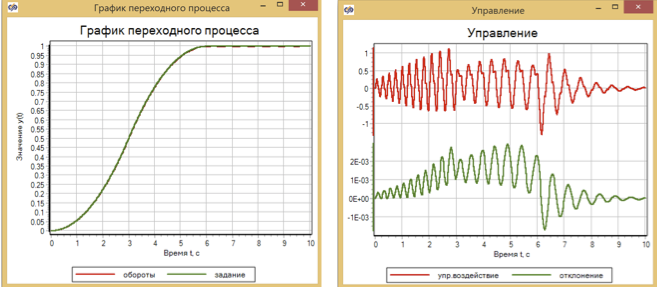
Рисунок 10. Переходный процесс и управление двигателем с помощью нечеткой логики.

Максимальное отклонение оборотов от заданных после оптимизации составило 2,5?10^-3. Что в принципе неплохо, однако в книге В.И. Гостева отклонения в модели после настроек были на два порядка меньше: максимальное составило 5?10^-5.

Для сравнения приведем результаты работы ПИД регулятора рис.11 и ПДД рис.12 для этой же модели упрощенной двигателя. Параметры данных регуляторов подбирались также методом оптимизации.

В результате для регулятора ПИД получено большее отклонение, чем для регулятора на базе нечеткой логики – примерно 6?10^-3, а для регулятора ПДД, который использует вторую производную, отклонение получилось примерно 3?10^-3 (см. 13). При этом на всех графиках видно, что при изменении заданного воздействия (изменения на участках 3 сек, 6 сек) качество регулирования меняется.

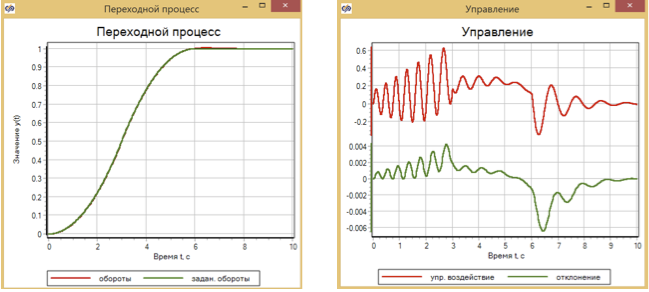
Рисунок 11. Переходный процесс и управление двигателем с помощью ПИД регулятора.

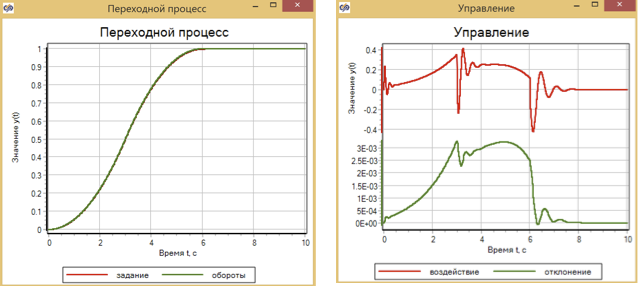
Рисунок 12. Переходный процесс и управление двигателем с помощью ПДД регулятора.

Для пуска двигателя используется задание переходной функции в виде плавного изменения оборотов. Регуляторы мы также настроили методом оптимизации на оптимальное управление именно по этому закону. Попробуем подать ступенчатое воздействие и посмотреть, как справятся регуляторы, изначально оптимизированные под плавный переходный процесс.

В качестве воздействия используем ступеньку с 0 до 1 на 3 секунде процесса.

Результаты эксперимента представлены на рисунках 13 – 15.

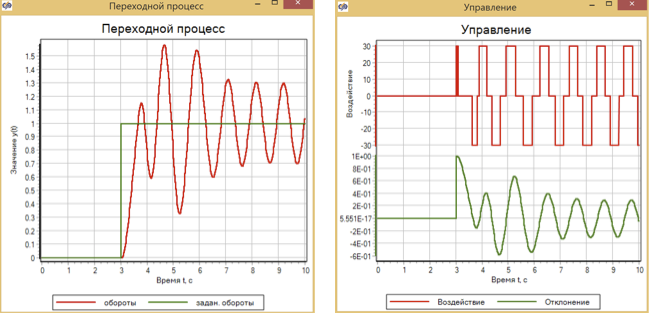
Рисунок 13. Переходный процесс и управление при ступенчатом управляющем воздействии с регулятором нечеткой логики.

Видно, что регулятор, настроенный на плавный разгон двигателя, при ступенчатом воздействии не справляется с управлением, и система выходит в режим автоколебаний.

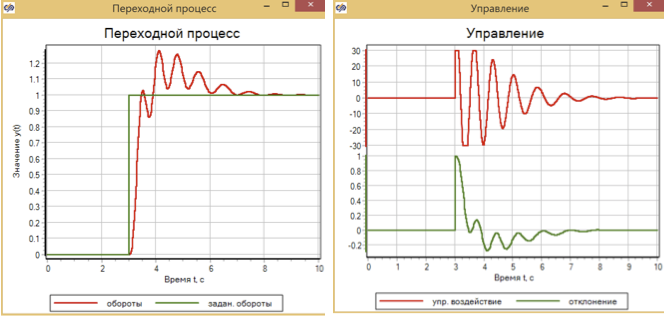
Рисунок 14. Переходный процесс и управление при ступенчатом управляющем воздействии с регулятором ПИД.

Регулятор ПИД, настроенный на плавный процесс, при ступенчатом воздействии обеспечивает переход в заданное время, но при этом происходит перерегулирование на 30% и колебательный процесс в течении 4-х секунд.

Регулятор ПДД, настроенный на плавное регулирование, при ступенчатом воздействии обеспечивает плавный переход без перерегулирования (рис. 14)

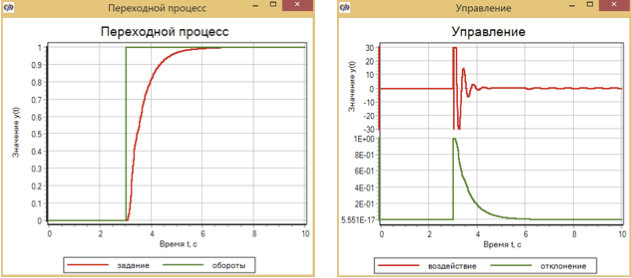
Рисунок 15. Переходный процесс и управление при ступенчатом управляющем воздействии с регулятором ПДД.

Выводы

Приведённые численные эксперименты показали, что регулятор на базе нечеткой логики обеспечивает более точное регулирование оборотов простой модели двигателя при плавном изменении заданного значения, чем ПИД и ПДД.

Однако, такая настройка, как оказалось, не гарантирует устойчивости регулятора при ступенчатом воздействии.

При этом для упрощенной модели двигателя регулятор на базе нечёткой логики в случае ступенчатого воздействия оказался хуже, чем регулятор ПИД или ПДД.

Ссылка на архив с проектам из статьи для самостоятельного изучения