«Зато мы делаем ракеты!»
В предыдущей статье я проверил, можно ли автоматически настраивать нечеткий регулятор, «стандартными методами» оптимизации. Оказалось можно и результат автоматической настройки вполне удовлетворительный. По крайней мере для ракеты, модель которой была использована.
Для нестационарных объектов управления где параметры объекта изменяются в широких диапазонах, нечеткий регулятор может не обеспечивать достаточное качество управления во всех диапазонах работы. В этом случае необходимо использовать нечёткий регулятор с «многоканальной настройкой».
Проверим возможно ли настроить такой регулятор стандартными методами оптимизации.
Рассмотрим синтез нечеткого регулятора с многоканальной настройкой для стабилизации баллистической ракеты по углу тангажа. Как подсказали в комментариях ракета будет ФАУ-2. Используем пример из той же книге Гостева В.В. «Нечеткие регуляторы в системах автоматического регулирования».
Все термины использованные в данном тексте взяты из этой книги и могут не соответствовать строгой терминологии теории автоматического управления.
Баллистическая ракета, в которой используется большое число локальных систем управления, является существенно не стационарным объектом управления. Передаточные функции, которыми описывают ракету как объект управления, отличаются от передаточных функций крылатых летательных аппаратов тем, что имеют неустойчивые звенья, поэтому движение неуправляемой ракеты по программной траектории было бы неустойчивым.
Ниже рассматривается система стабилизации баллистической ракеты по углу тангажа (каналу продольного движения). Система состоит из следующих функционально необходимых элементов:
элемента сравнения (свободного гироскопа с потенциометрическим датчиком, характеризуемым коэффициентов Кп);
усилителя с коэффициентом усиления Ку, и гидравлического рулевого механизма.
Приняв за выходную координату ракеты угол тангажа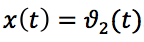
, за входную координату – угол поворота руля 
, определим передаточную функцию в виде:
(В объект управления включены аналоговые рулевой механизм и ракета) Параметры передаточной функции будут полиномами, зависящимися от времени. Математически их можно определить полиномами:
В задаче принимается, что время начала полета соответствует 6 секунде. Значения полином принимаются со сдвигом на 6 секунда.
Математическая модель нестационарного колебательного звена описывается дифференциальным уравнением:
Математическая модель нестационарного форсирующего звена описывается дифференциальным уравнением:
Ошибка рассогласования, поступающая на вход нечеткого регулятора, является разностью между заданными и требуемым углом тангажа.
Структурная схема модели представлена на рисунке 1. Чтобы был понятен принцип формирования модели, на линиях связи указаны переменные Х1, Х и их производные (Х1’’, Х1'', X') согласно уравнениям звеньев. Зеленым прямоугольником обозначена часть схемы модели, соответствующая колебательному звену, желтым – форсирующему.
Параметры a(t),b(t),c(t),r(t) задаются в виде коэффициентов усиления, в блоках типа «усилитель». Параметр
задается в коэффициенте усиления интегрирующего звена.
Рисунок 1. Структурная схема модели.
Программная траектория, заданный угол тангажа u(t) = 1+0.5sin(?t/30).
Графики изменения параметров ракеты в процессе полета представлены на рисунке 2.
В качестве начала полета принимается значение t = 6, в функции полиномов для расчета параметров используется значение (time+6), где time – текущее время моделирования.
Рисунок 2. Графики изменения параметров ракеты.
В качестве регулятора на базе нечеткой логики используем регулятор, представленный на рисунке 3. На вход подается рассогласование между заданным углом тангажа и реальным, отработанным ракетой, углом тангажа.
Блок задержка на шаг квантования обеспечивает дискретизацию преобразования непрерывного сигнала в дискретный с шагом дискретизации 0.01 сек.
Используя еще две задержки, на шаг дискретизации производится вычисление разностными методами первой и второй производной отклонения.
Блоки фазификации осуществляют расчет значений термов для отклонения, скорости изменения и ускорения. (Более подробно об этом см. предыдущей текст). На выходе из каждого блока фазифкации мы получаем вектор термов для лингвистических переменных. (см. таблицу 1)
Блоки демультиплексоры разбирают вектора на отдельные термы, которые передаются в блоки логической обработки согласно правил нечеткого вывода.
Результат работы нечеткого вывода тоже имеет три лингвистические переменные: «уменьшать», «не изменять», «увеличивать». В виде схемы записаны следующие правила логического вывода.
Рисунок 3. Схема реуглятора на базе нечеткой логики.
В качестве функции принадлежности при денацификации используются треугольные функции с общим основанием (см. рис. 4)
Рисунок 4. Треугольные функции фазификации с общим основанием.
Принимается, что функции симметричны относительно 0, в этом случае для описания трех треугольных функций достаточно одного значения Мах. Для приведенных на рисунке Мaх = 30.
Для вывода используются такие же функции принадлежности.
Для полного определения регулятора необходимо задать максимальные значения для блоков фазификации переменных:
— deltaMax – максимальное отклонение;
— divMax – максимальна производная отклонения;
— div2Max – максимальная вторая производная отклонения;
— uMaх – максимальное управляющее воздействие.
Максимальное управляющее воздействие принимаем равным uMaх — 70.
Таким образом, нам остается подобрать 3 параметра для функции фазифкации.
В данной задаче у нас рассогласование подается ступенькой в нулевой момент модельного времени, u(t) = 1+0.5.sin(?t/30).
Программная траектория, заданный угол тангажа u(t) = 1+0.5sin(?t/30), вызывает ступенчатое воздействие на первой секунде переходного процесса, как выяснилось при опытах с предыдущей задачей, регуляторы, настроенные на плавных процесс управления, при ступенчатом воздействии могут не обеспечивать требуемое качество переходного процесса.
Поэтому для оптимизации мы формируем 3 критерия:
Общая схема блока оптимизации представлена на рисунке 5.
Рисунок 5. Схема блока оптимизации.
Входные параметры блока оптимзации:
— отклонение от заданного угла тангажа.
— регулирующего воздействия.
Для вычисления времени переходного процесса используется переключатель, в котором на один из входов подается текущее модельное время. После блока стоит задержка на период квантования, значение с задержки передается на второй вход.
В качестве переключения используется модуль отклонения. Если модуль отклонения больше заданного значения переключения (0.02) то на выходе из блока подается текущее время, если модуль меньше заданного значения то на выход передается время запомненное, когда отклонение было больше. Если далее отклонение снова превысит предел, мы снова получим время. Таким образом, на выходе у нас всегда последнее время, когда отклонение превышало заданное.
В качестве единицы переключения принято изменения знака управляющего воздействия с + на -. Для вычисления количества переключений используем блок «импульс по фронту» который при изменении входа с 0 до 1 выдает импульс длительностью в шаг интегрирования, подсчет импульсов выполняется интегратором. На выходе из блока — количество переключений.
— Блок оптимизации подбирает значения оптимизируемых параметров таким образом, что бы минимизировать все три параметра:
— deltaMax – максимальное отклонение;
— divMax – максимальна производная отклонения;
— div2Max – максимальная вторая производная отклонения.
Запустив процесс оптимизации, мы получили следующие оптимальные параметры для нечеткого регулятора:
— deltaMax = 0.185– максимальное отклонение;
— divMax = 0.278 – максимальна производная отклонения;
— div2Max = 1.291 – максимальная вторая производная отклонения.
Результаты оптимизированного процесса приведены на рисунке 6.
Видно, что оптимизация, в целом, удалась, но отклонения от заданного угла тангажа есть практически на всем протяжении процесса. Укрупненный график отклонения показывает, что отклонения после оптимизации и завершения переходного процесса находятся в передела 0.015 — 0.02. (см. рис. 7)
Рисунок 7. Отклонение в процессе управления.
Попробуем улучшить процесс за счет подбора параметров нечеткого регулятора для разных участков полета ракеты.
Первый участок – это время со старта до выхода на заданную траекторию. Исходя из графика отклонения, переходной процесс, связанный с начальным ступенчатым воздействием, заканчивается где-то при 20 сек. (см. рис. 7). На этом участке происходит оптимизация по времени переходного процесса.
Установим время окончания расчета 20 сек. И выполним оптимизации, убрав из критериев среднеквадратичное отклонение. Оптимизировать будем по времени переходного процесса и количества переключений. Схема блока оптимизации приведена на рисунке 8.
Рисунок 8. Схема оптимизация на первом участке полета.
Автоматическая оптимизация для первого участка полета до 20 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.056– максимальное отклонение;
— divMax = 0.0968 – максимальна производная отклонения;
— div2Max = 0.987 – максимальная вторая производная отклонения.
Переходной процесс после оптимизации представлен на рисунке 9.
Отклонение в увеличенном масштабе представлены на рисунке 10
Рисунок 10. Отклонение в увеличенном масштабе первого участка полета.
На графиках видно, что уменьшилась величина перерегулирования и отклонение после завершения переходного процесса стало меньше 0.005.
Для оптимизации на следующем участке полета мы выполним моделирование с сохраненным состоянием, полученным на первом участке.
Моделирование происходит с 20 по 40 секунду полета баллистической ракеты, оптимизация происходит по всему процессу.
Поскольку у нас к началу второго участка переходной процесс завершён, мы осуществляем оптимизацию только по отклонению и количеству переключений. Схема блока оптимизации представлена на рисунке 11.
Рисунок 11. Схема оптимизации на втором участке полета.
Автоматическая оптимизация для второго участка полета от 20 до 40 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.056– максимальное отклонение;
— divMax = 0.0974 – максимальна производная отклонения;
— div2Max = 0.980 – максимальная вторая производная отклонения.
При заданных параметрах отклонение угла тангажа от заданного уменьшается на всем втором временном участке полета. Но если использовать полученные оптимизацией на втором участке полета параметры для управления до 66 секунды, то видно, что точность начинает снижется и отклонение начинает расти после 40 секунды (см. рис. 12).
Рисунок 12. Процесс управления баллистической ракетой с настройками, оптимизированными на 20-40 секунду полета.
Повторим оптимизацию для третьего участка полета. Сохраним результаты 40 секунды.
Используем их для старта и оптимизации на участке от 40 до 66 секунды.
Автоматическая оптимизация для последнего участка полета от 40 до 66 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.0146– максимальное отклонение;
— divMax = 0.0157– максимальна производная отклонения;
— div2Max = 0.555 – максимальная вторая производная отклонения.
График процесса управления на последнем участке полета баллистической ракеты после оптимизации представлен на рисунке 13.
Рисунок 13. Процесс управления баллистической ракетой на последнем участке полета.
Из рисунка 13 видно, что при новых настройках отклонение на временном отрезке полета 40-66 секунд не увеличивается, в отличие от настроек оптимизированных на второй участок полета (см. рис.12).
Таким образом, мы получили настройки нечеткого регулятора для трех участков полета. Давайте создадим переключатель режимов, который будет переключать настройки регулятора в процессе полета. Схема переключателя режимов изображена на рисунке 14
Рисунок 14. Переключатель режимов нечеткого регулятора баллистической ракеты.
Переключение режимов у нас будет происходить по времени, в верхней части простая логическая схема осуществляет сравнение текущего модельного времени с точками переключения. В результате в мултиплексоре формируется управляющий вектор из трех значений. В данном векторе значение 1 находится на позиции текущего временного интервала.
Рассчитанные ранее методами оптимизации параметры нечеткого регулятора упакованы в вектора из трех значений.
С помощью блока выборки из трех значений выбирается то, которому в векторе управление соответствует 1. Таким образом, при изменении времени параметры, передаваемые в нечеткий регулятор, изменяются согласно текущему участку полета.
Для наглядности значения, передаваемые по линии связи, отображены на схеме. Рисунок соответствует последнему участку полета баллистической ракеты. Время больше 40 сек. Вектор управления (0,0,1) в регулятор подается последний параметр из набора.
Результат моделирования управления углом тангажа ракеты с переключением параметров регулятора представлен на рисунке 15.
Выводы:
Регулятор на базе нечеткой логики может быть настроен методом оптимизации на работу в режим переключения параметров.
Отклонение при работе с переменными параметрами в приведённом примере уменьшились в 3 – 5 раз по сравнению с работой регулятора с постоянными параметрами.
Архив с проектами для самостоятельного изучения можено скачать здесь...
В предыдущей статье я проверил, можно ли автоматически настраивать нечеткий регулятор, «стандартными методами» оптимизации. Оказалось можно и результат автоматической настройки вполне удовлетворительный. По крайней мере для ракеты, модель которой была использована.
Для нестационарных объектов управления где параметры объекта изменяются в широких диапазонах, нечеткий регулятор может не обеспечивать достаточное качество управления во всех диапазонах работы. В этом случае необходимо использовать нечёткий регулятор с «многоканальной настройкой».
Проверим возможно ли настроить такой регулятор стандартными методами оптимизации.
Рассмотрим синтез нечеткого регулятора с многоканальной настройкой для стабилизации баллистической ракеты по углу тангажа. Как подсказали в комментариях ракета будет ФАУ-2. Используем пример из той же книге Гостева В.В. «Нечеткие регуляторы в системах автоматического регулирования».
Все термины использованные в данном тексте взяты из этой книги и могут не соответствовать строгой терминологии теории автоматического управления.
Постановка задачи
Баллистическая ракета, в которой используется большое число локальных систем управления, является существенно не стационарным объектом управления. Передаточные функции, которыми описывают ракету как объект управления, отличаются от передаточных функций крылатых летательных аппаратов тем, что имеют неустойчивые звенья, поэтому движение неуправляемой ракеты по программной траектории было бы неустойчивым.
Ниже рассматривается система стабилизации баллистической ракеты по углу тангажа (каналу продольного движения). Система состоит из следующих функционально необходимых элементов:
элемента сравнения (свободного гироскопа с потенциометрическим датчиком, характеризуемым коэффициентов Кп);
усилителя с коэффициентом усиления Ку, и гидравлического рулевого механизма.
Приняв за выходную координату ракеты угол тангажа
, за входную координату – угол поворота руля , определим передаточную функцию в виде:(В объект управления включены аналоговые рулевой механизм и ракета) Параметры передаточной функции будут полиномами, зависящимися от времени. Математически их можно определить полиномами:
В задаче принимается, что время начала полета соответствует 6 секунде. Значения полином принимаются со сдвигом на 6 секунда.
Математическая модель нестационарного колебательного звена описывается дифференциальным уравнением:
Математическая модель нестационарного форсирующего звена описывается дифференциальным уравнением:
Ошибка рассогласования, поступающая на вход нечеткого регулятора, является разностью между заданными и требуемым углом тангажа.
Структурная схема модели представлена на рисунке 1. Чтобы был понятен принцип формирования модели, на линиях связи указаны переменные Х1, Х и их производные (Х1’’, Х1'', X') согласно уравнениям звеньев. Зеленым прямоугольником обозначена часть схемы модели, соответствующая колебательному звену, желтым – форсирующему.
Параметры a(t),b(t),c(t),r(t) задаются в виде коэффициентов усиления, в блоках типа «усилитель». Параметр
задается в коэффициенте усиления интегрирующего звена.Рисунок 1. Структурная схема модели.
Программная траектория, заданный угол тангажа u(t) = 1+0.5sin(?t/30).
Графики изменения параметров ракеты в процессе полета представлены на рисунке 2.
В качестве начала полета принимается значение t = 6, в функции полиномов для расчета параметров используется значение (time+6), где time – текущее время моделирования.
Рисунок 2. Графики изменения параметров ракеты.
Регулятор на базе нечеткой логики
В качестве регулятора на базе нечеткой логики используем регулятор, представленный на рисунке 3. На вход подается рассогласование между заданным углом тангажа и реальным, отработанным ракетой, углом тангажа.
Блок задержка на шаг квантования обеспечивает дискретизацию преобразования непрерывного сигнала в дискретный с шагом дискретизации 0.01 сек.
Используя еще две задержки, на шаг дискретизации производится вычисление разностными методами первой и второй производной отклонения.
Блоки фазификации осуществляют расчет значений термов для отклонения, скорости изменения и ускорения. (Более подробно об этом см. предыдущей текст). На выходе из каждого блока фазифкации мы получаем вектор термов для лингвистических переменных. (см. таблицу 1)
| Лингвистическая переменная | Термы |
| Отклонение | Больше Норма Меньше |
| Скорость изменения | Растет Не изменяется Падает |
| Ускорение изменения | Увеличивается Постоянна Уменьшается |
Результат работы нечеткого вывода тоже имеет три лингвистические переменные: «уменьшать», «не изменять», «увеличивать». В виде схемы записаны следующие правила логического вывода.
- Если Больше и Растет и скорость роста увеличивается => уменьшаем.
- Если норма, и не изменяется и постоянна => не изменяем.
- Если Меньше и Падает и скорость падения увеличивается => увеличиваем.
Рисунок 3. Схема реуглятора на базе нечеткой логики.
В качестве функции принадлежности при денацификации используются треугольные функции с общим основанием (см. рис. 4)
Рисунок 4. Треугольные функции фазификации с общим основанием.
Принимается, что функции симметричны относительно 0, в этом случае для описания трех треугольных функций достаточно одного значения Мах. Для приведенных на рисунке Мaх = 30.
Для вывода используются такие же функции принадлежности.
Для полного определения регулятора необходимо задать максимальные значения для блоков фазификации переменных:
— deltaMax – максимальное отклонение;
— divMax – максимальна производная отклонения;
— div2Max – максимальная вторая производная отклонения;
— uMaх – максимальное управляющее воздействие.
Оптимизация по полному процессу
Максимальное управляющее воздействие принимаем равным uMaх — 70.
Таким образом, нам остается подобрать 3 параметра для функции фазифкации.
В данной задаче у нас рассогласование подается ступенькой в нулевой момент модельного времени, u(t) = 1+0.5.sin(?t/30).
Программная траектория, заданный угол тангажа u(t) = 1+0.5sin(?t/30), вызывает ступенчатое воздействие на первой секунде переходного процесса, как выяснилось при опытах с предыдущей задачей, регуляторы, настроенные на плавных процесс управления, при ступенчатом воздействии могут не обеспечивать требуемое качество переходного процесса.
Поэтому для оптимизации мы формируем 3 критерия:
- Время переходного процесса – мы должны как можно быстрее выйти на заданную программную траекторию.
- Среднеквадратичное отклонение.
- Количество переключений – в экспериментах с предыдущей задачей мы получили вариант, когда в системе управления на выходе были высокочастотные колебания управляющего воздействия.
Общая схема блока оптимизации представлена на рисунке 5.
Рисунок 5. Схема блока оптимизации.
Входные параметры блока оптимзации:
— отклонение от заданного угла тангажа.
— регулирующего воздействия.
Для вычисления времени переходного процесса используется переключатель, в котором на один из входов подается текущее модельное время. После блока стоит задержка на период квантования, значение с задержки передается на второй вход.
В качестве переключения используется модуль отклонения. Если модуль отклонения больше заданного значения переключения (0.02) то на выходе из блока подается текущее время, если модуль меньше заданного значения то на выход передается время запомненное, когда отклонение было больше. Если далее отклонение снова превысит предел, мы снова получим время. Таким образом, на выходе у нас всегда последнее время, когда отклонение превышало заданное.
В качестве единицы переключения принято изменения знака управляющего воздействия с + на -. Для вычисления количества переключений используем блок «импульс по фронту» который при изменении входа с 0 до 1 выдает импульс длительностью в шаг интегрирования, подсчет импульсов выполняется интегратором. На выходе из блока — количество переключений.
— Блок оптимизации подбирает значения оптимизируемых параметров таким образом, что бы минимизировать все три параметра:
— deltaMax – максимальное отклонение;
— divMax – максимальна производная отклонения;
— div2Max – максимальная вторая производная отклонения.
Результат оптимизация по полному переходному процессу.
Запустив процесс оптимизации, мы получили следующие оптимальные параметры для нечеткого регулятора:
— deltaMax = 0.185– максимальное отклонение;
— divMax = 0.278 – максимальна производная отклонения;
— div2Max = 1.291 – максимальная вторая производная отклонения.
Результаты оптимизированного процесса приведены на рисунке 6.
 Рисунок 6а. Переходной процесс. |
 Рисунок 6б. Параметры управления. |
Видно, что оптимизация, в целом, удалась, но отклонения от заданного угла тангажа есть практически на всем протяжении процесса. Укрупненный график отклонения показывает, что отклонения после оптимизации и завершения переходного процесса находятся в передела 0.015 — 0.02. (см. рис. 7)
Рисунок 7. Отклонение в процессе управления.
Оптимизация по участкам полета.
Попробуем улучшить процесс за счет подбора параметров нечеткого регулятора для разных участков полета ракеты.
Первый участок – это время со старта до выхода на заданную траекторию. Исходя из графика отклонения, переходной процесс, связанный с начальным ступенчатым воздействием, заканчивается где-то при 20 сек. (см. рис. 7). На этом участке происходит оптимизация по времени переходного процесса.
Установим время окончания расчета 20 сек. И выполним оптимизации, убрав из критериев среднеквадратичное отклонение. Оптимизировать будем по времени переходного процесса и количества переключений. Схема блока оптимизации приведена на рисунке 8.
Рисунок 8. Схема оптимизация на первом участке полета.
Автоматическая оптимизация для первого участка полета до 20 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.056– максимальное отклонение;
— divMax = 0.0968 – максимальна производная отклонения;
— div2Max = 0.987 – максимальная вторая производная отклонения.
Переходной процесс после оптимизации представлен на рисунке 9.
Отклонение в увеличенном масштабе представлены на рисунке 10
 Рисунок 9а. Переходной процесс. |
 Рисунок 9б. Параметры управления. |
Рисунок 10. Отклонение в увеличенном масштабе первого участка полета.
На графиках видно, что уменьшилась величина перерегулирования и отклонение после завершения переходного процесса стало меньше 0.005.
Для оптимизации на следующем участке полета мы выполним моделирование с сохраненным состоянием, полученным на первом участке.
Моделирование происходит с 20 по 40 секунду полета баллистической ракеты, оптимизация происходит по всему процессу.
Поскольку у нас к началу второго участка переходной процесс завершён, мы осуществляем оптимизацию только по отклонению и количеству переключений. Схема блока оптимизации представлена на рисунке 11.
Рисунок 11. Схема оптимизации на втором участке полета.
Автоматическая оптимизация для второго участка полета от 20 до 40 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.056– максимальное отклонение;
— divMax = 0.0974 – максимальна производная отклонения;
— div2Max = 0.980 – максимальная вторая производная отклонения.
При заданных параметрах отклонение угла тангажа от заданного уменьшается на всем втором временном участке полета. Но если использовать полученные оптимизацией на втором участке полета параметры для управления до 66 секунды, то видно, что точность начинает снижется и отклонение начинает расти после 40 секунды (см. рис. 12).
Рисунок 12. Процесс управления баллистической ракетой с настройками, оптимизированными на 20-40 секунду полета.
Повторим оптимизацию для третьего участка полета. Сохраним результаты 40 секунды.
Используем их для старта и оптимизации на участке от 40 до 66 секунды.
Автоматическая оптимизация для последнего участка полета от 40 до 66 секунд выдала такие параметры для нечеткого регулирования:
— deltaMax = 0.0146– максимальное отклонение;
— divMax = 0.0157– максимальна производная отклонения;
— div2Max = 0.555 – максимальная вторая производная отклонения.
График процесса управления на последнем участке полета баллистической ракеты после оптимизации представлен на рисунке 13.
Рисунок 13. Процесс управления баллистической ракетой на последнем участке полета.
Из рисунка 13 видно, что при новых настройках отклонение на временном отрезке полета 40-66 секунд не увеличивается, в отличие от настроек оптимизированных на второй участок полета (см. рис.12).
Таким образом, мы получили настройки нечеткого регулятора для трех участков полета. Давайте создадим переключатель режимов, который будет переключать настройки регулятора в процессе полета. Схема переключателя режимов изображена на рисунке 14
Рисунок 14. Переключатель режимов нечеткого регулятора баллистической ракеты.
Переключение режимов у нас будет происходить по времени, в верхней части простая логическая схема осуществляет сравнение текущего модельного времени с точками переключения. В результате в мултиплексоре формируется управляющий вектор из трех значений. В данном векторе значение 1 находится на позиции текущего временного интервала.
Рассчитанные ранее методами оптимизации параметры нечеткого регулятора упакованы в вектора из трех значений.
С помощью блока выборки из трех значений выбирается то, которому в векторе управление соответствует 1. Таким образом, при изменении времени параметры, передаваемые в нечеткий регулятор, изменяются согласно текущему участку полета.
Для наглядности значения, передаваемые по линии связи, отображены на схеме. Рисунок соответствует последнему участку полета баллистической ракеты. Время больше 40 сек. Вектор управления (0,0,1) в регулятор подается последний параметр из набора.
Результат моделирования управления углом тангажа ракеты с переключением параметров регулятора представлен на рисунке 15.
 Рисунок 15а. Переходной процесс. |
 Рисунок 15б. Параметры управления. |
Выводы:
Регулятор на базе нечеткой логики может быть настроен методом оптимизации на работу в режим переключения параметров.
Отклонение при работе с переменными параметрами в приведённом примере уменьшились в 3 – 5 раз по сравнению с работой регулятора с постоянными параметрами.
Архив с проектами для самостоятельного изучения можено скачать здесь...
FGV
Если я правильно понял то коэф. нестационарного объекта побили на интервалы и для каждого интервала посчитали оптимальные коэф. для нечеткого регулятора.
Собственно вопрос, а что мешает тоже самое сделать в случае классического ПИД регулятора? ну и сравнить результаты.
Arastas
Ещё стоит отметить, что фаззи, на сколько я понимаю автора, — статический регулятор, а ПИД — динамический. То есть ПИД сможет ещё и компенсацию возмущения дать.
FGV
с одной стороны интеграторов — нет, астатизм 0 порядка должен быть; с другой стороны регулятор — нелинейный, незнаю насколько к нему будет применимо определение "статический".
Arastas
Я никогда не занимался всерьёз фази системами, так что могу упускать какие-то нюансы. Но на мой взгляд, там происходит следующее. Система нечёткой логики принимает на вход три сигнала и выдаёт на выход один сигнал. У системы нет собственных внутренних состояний (нелинейность без памяти), преобразование детерминированное. То есть для одних и тех же входных сигналов мы всегда будем получать один и тот же выходной сигнал. Фактически, мы говорим о некоторой функции R^3 -> R. Это и есть статический нелинейный регулятор по состоянию. Причём, на сколько я понимаю, функция получается непрерывная.
Далее, как я понимаю, фази логика со всеми лингвистическими переменными это просто способ параметризировать нелинейную функцию. Своеобразный и типа как обладающий инженерным смыслом. Но, в конечном итоге, всё сводится к параметризации нелинейной функции обратной связи и оптимизации парамтров.
Можно взять другую параметризацию, например на нейронных сетях. Причем, так как и то и то является универсальным аппроксиматором, то должна существовать нейронная сеть, в точности повторяющая настроенную нечёткую логику. Можно даже какой-то свой функциональный базис придумать, но это всё равно останется нелинейная статическая функция состояния.
petuhoff Автор
Все верно. В Фази даже веса есть, как в нейронных сетях, для учета каждого правила в обще базе. И в данном случае это дейстивтельно статическая функция состояния.
Но нам ничего не мешает завести в качестве переменных в эту функцию например положение управляющиего элемента. Наприме ввести правило, если угол отклонения рулей большой, то уменьшаем. Тогда одним из параметров функции управления будет интегральная составляющая как в ПИД.
Arastas
Конечно никто не мешает расширить пространство состояний, введя ещё один интегратор. Просто в статье этого нет, а сравнивать предлагали с ПИД, у которого есть. Я и отметил это отличие.
petuhoff Автор
Не настраивается почему то дискретный ПИД даже на первом участке.
FGV
Очень странно. Из тех нестационарных систем, что видел, обычно делают так:
1) фиксируют характеристики объекта управления в определенных точках в зависимости от параметра (скорость, масса, время, и.т.д.) в данном случае это время, например: t=0, 2, 4, …;
2) для каждого фиксированного объекта считают регулятор (обычно ПИ);
3) коэффициенты регулятора вводят как функции от параметра.
И самое главное — можно оценить запасы устойчивости! (как это делать для нечеткой логики честно говоря не представляю).
petuhoff Автор
Зафиксировал параметры переменные (взял те которые при 10 сек) ПИД все равно не настраивается даже когда параметры постоянны.
FGV
ну да, интегратор же на входе, поэтому только пропорциональный регулятор
FGV
а, просмотрел, у Вас ведь есть неустойчивые корни. Кстати откуда? физически это что за системы?
petuhoff Автор
Это баллистическая ракета, передаточная функция по углу тангажа. Я ее готовую взял из книги.Гостев В.И. нечеткая логика в системах управленич
FGV
открыл книгу, вижу:
т.е. ни одного неустойчивого звена, вопрос, откуда у Вас взялся довесок:
W(s) = (s+r) / (s+c)
и еще с отрицательным c?
petuhoff Автор
Это предыдущий пример тут угол атаки, а многоканалный регулятор в этой книге следующий, там угол тангажа.
FGV
Разобрался. Исходная система не устойчива — как минимум имеет два неустойчивых полюса (при t=0). Собсно вместо регулятора надо ставить корректирующее звено, тогда система станет устойчивой в замкнутом виде.
p.s. кстати баллистическая ракета тут — фау-2.
FGV
система с корр. звеном для t=0:
и ее реакция на 1 скачек:
шаг сетки по времени — 1e-5.
petuhoff Автор
А как подбирать параметры коректирующего звена?
FGV
В ТАУ есть куча методов. Конкретно тут — звено подбирал исходя из устойчивости по Критерию Найквиста.
ЛАЧХ исходной, разомкнутой системы:
Т.к. разомкнутая система имеет два неустойчивых корня, то для того что бы замкнутая система была устойчивой — АФХ разомкнутой системы должна охватывать точку -1, с пересечением действительной оси против часовой стрелки один раз (синим — АФХ исходной системы, красным — желаемый АФХ):
ЛАЧХ разомкнутой системы с корр. звеном:
Arastas
Если у вас система с переменными параметрами, которая устойчива для каждого фиксированного значения параметров (объект в точке плюс ваш регулятор, посчитанный в этой точке), то отсюда, в общем случае, не следует устойчивость замкнутой системы при варьировании параметра.
FGV
Коэф. регулятора/корр. звена изменяются вместе с параметрами системы, так что должна быть устойчивой.
Arastas
Нет, я так не думаю. Даже в относительно простом случае, когда у вас варьируемый параметр может принимать только два значения, и для каждого из значений вы посчитали регулятор и получили устойчивую систему второго порядка или выше, то неудачная последовательность моментов переключения может привести к неустойчивости системы.
FGV
Тут параметры системы не меняются скачком, а плавно тихой сапой ползут (центровка по мере выработки топлива меняется, аэродинамика меняется в зависимости от маха).
Ну и зачем переключать коэф.? можно интерполировать, например линейно.
Arastas
Я пытаюсь сказать, что для системы с переменными параметрами в общем случае недостаточно показать, что для каждого момента времени система с фиксированными параметрами устойчива. Например, пусть у вас система второго порядка вида
Легко проверить, что для любого значения времени t матрица состояний Гурвицева, причем у неё постоянные собственные числа, -1 и -1. Что вы думаете про устойчивость этой системы?
Я не говорю про какой-то конкретный объект, у которого параметры меняются значительно медленнее, чем происходит управление. Я в целом о подходе.
FGV
а что ж еще требуется? хотя вобщем да, мало сказать устойчива или нет, неплохо бы еще показать запасы устойчивости по апмлитуде/фазе.
Не пойму о каком подходе речь.
Тут в статье кстати приведен занятный объект управления, аж 1942года разработки, очень сомневаюсь что тогда применяли нечеткую логику, наверняка что то аналогомеханическое было, из классического ТАУ.
Arastas
Вы посмотрели пример, который я привел? Для любого фиксированного t соответствующая система с "замороженными" параметрами устойчива. Попробуйте её промоделировать когда t это время.
FGV
чую тут дело в том что в модели параметры системы существенно меняются вместе с управляющим воздействием, короче говоря система существенно нестационарна и методы классического ТАУ к ней вероятно вообще неприменимы.
Собсно в статье приводится так называемый "квазистационарный" объект, т.е. такой для которого метод замораживания коэффициентов годится.
Arastas
Ну потому я и сказал, что в общем случае. :)
Интересно, сктати, что в самой статье вопрос устойчивости замкнутой системы с фази регулятором вообще не обсуждается (на сколько я вижу).
petuhoff Автор
Да устойчивость тут не рассматривается вообще. Никаких анализов корней и годографов по феншую. Набрали модель и вперед — управлять. Но то, что система неустойчива, видно когда работает оптимизация подбором там график разлетается очень часто.
petuhoff Автор
попробую сделать в ближайшее время.