08.11.2018 18:38
Oxoron 330 25300 Источник
В недавней статье товарищ KvanTTT поднял вопрос:
Можете пояснить что вам не нравится в современной записи (математических положений и) формул и как ее можно улучшить?
Я постарался ответить в одном комментарии, но размер текстового поля не позволил закончить выкладки. Данная статья — чрезмерно развернутый ответ.

Сразу скажу, материал холиварный. Местами слишком эмоциональный. Очень спорный. Слишком личный — часто основан на собственном опыте, небогатом, хоть и разнообразном. Пост касается школьных и университетских текстов учебников: у «профессиональной» литературы своя специфика, своя аудитория. Решения у проблемы в текущих реалиях нет. При этом, часть «моих» наблюдений задолго до меня высказывали такие авторитеты, как Кнут и Хэмминг; чуть менее популярные ребята даже запилили инструкцию "Как читать математику".

Итак, на мой взгляд, основные претензии не столько к записи формул, сколько к подаче материала. Причем, к подаче материала на практически всех уровнях образования, начиная со школы, и заканчивая передовой наукой. Начало текущей ситуации положил Евклид, заявивший про отсутствие царской дороги в математике. Царскую дорогу не проложили до сих пор. Евклид обходился, и мы сможем.

Первая проблема — значимость не показана. Еще один подарок от Евклида: «Дай вопрошающему грош, если он ищет выгоды, а не математики». Авторы начинают вводить определения, доказывать теоремы и творить прочую математику без объяснения зачем оно вообще нужно. Пример: учебник по математическому анализу от Фихтенгольца. Почитайте первую главу: «из школьного курса вы знаете про рациональные числа, но потребности математики понуждают нас ввести вещественные...» и понеслась. Какие потребности, какой математики, чем не устраивают рациональные — да пес его знает. «Очевидно».

Или другой пример из того же учебника. «Постоянное число a называется пределом варианты $x=x_n$ если для каждого положительного $\varepsilon$ сколько бы мало оно ни было, существует такой номер N, что все значения $x_n$, у которых номер n>N, удовлетворяет равенству $|x_n - a | < \varepsilon$.»

Большинство студентов не понимает определения выше, но через полгода привыкает к нему. Еще больше студентов даже к концу обучения не осознает, зачем им было нужно понятие предела последовательности. Аналогично для функций, интегралов, рядов… Фихтенгольц описывает какие-то математические объекты, иногда дает частные примеры — и все. Ну да, сейчас мне понятно, что пределы нужны, например, для корректного описания верхних/нижних сумм при введении интегралов, но до интегралов еще два семестра!

Или определитель, определяемый как кососимметрическая полилинейная функция. Ребята, вы это серьезно? Единственный адекватный ответ студента-первокурсника на такой определение «и что»? Выгода какая с этого определения? Не спорю, выгода есть, но всякий ли первокурсник может её осознать?

Ложное решение проблемы: история вопроса. Проявляется на всякого рода конференциях. «Проблему поставил Иаков, исследовал его ученик Авель, и ученик ученика Каин, и сто-пятьсот воплощений Вишны». В чем суть проблемы, почему её решал первоначальный автор, почему так важно убивать на неё профессоро-часы — опускается.

Следующая проблема — авторы не ставят реальных проблем


В принципе, схожа с предыдущей. Вспомните курс теории вероятностей. Какие там преобладают задачи? «В корзине лежат 25 черных и 10 белых шаров...». Казиношные примеры, карточные, D&D, экономические — не, не слышали. Мы будем использовать максимально политкорректные примеры, хоть теория вероятностей выросла из исследований игры в кости.

Про живые примеры недавно писала Free_Mic_RS

Я преподавала статистику и фин.анализ...
Я преподавала статистику и фин.анализ у относительно гуманитарных ребят. Это было довольно сложно — видеть 30-90 пар пустых глаз. Меня саму начинало мутить от их беспросветного непонимания индексов, показателей и формул. Но, конечно, сообразительные ребятки были, и вот однажды я услышала, как один парень объяснял что-то сокурсникам: «Да вы уловите суть! Вы пришли в клуб и думаете, что все девушки там, как Анджелина Джоли. Идёте, а там у первой ноги короткие, у второй короткая стрижка, у третьей пятый размер, у четвёртой — нулевой, у пятой есть парень и т.д. И ни одна не Джоли, но из них её собрать можно. Но в целом это молодые девушки, с которыми можно приятно провести время. И вот то, насколько они далеки от идеала, определяет качество вашей вечеринки. В этом суть дисперсии — отклонения кучи циферок от самой главной циферки». Это было прекрасно, живо и весело. Я взяла опыт на вооружение и уже через неделю у нас был проектор с интересными презентациями и примерами, а аудитория не тупо записывала под бу-бу-бу и стук мела по доске, а искала примеры. Это была лучшая сессия за 2 года.

Математика начинается с задачи. И мертвые, однобокие задачи оставляют впечатление, что теор-вер только с ними и работает. Намерение авторов благое: дать пример, а потом перейти к общему. Абстрагировать от примера. Но несколько «живых» примеров сделали бы переход к абстракции гораздо полезнее. По крайней мере, я свято верю, что обратный процесс (переход от абстрактного к частному) проходил бы гораздо проще.

Проблема: излишняя краткость и непоследовательность


Помните школу? А формулу дискриминанта? А как она доказывается/выводится? Один из способов: чисто алгебраический. Берем уравнение $ax^2 + bx = -c$, «Умножаем каждую часть на $4a$ и прибавляем $b^2$» (почему именно на эти значения?), еще немного трансформаций — и готово. После дискриминанта ученикам дают дискриминант-для-четного-b. А потом формулы Виета. А ещё полные квадраты. И кучу примеров. И далеко не всегда объясняется, зачем нужны все эти методы.

А теперь представьте ситуацию, ученику говорят: «сегодня мы научимся решать уравнения с $x^2$. Любые.» И начинается серия примеров с усложнением.

$x^2 = 4\\ x^ 2 = 9\\ x^2 + 2x + 1 = 1\\ x^2 + 2x + 1 = 4\\ x^2 + 2x + 1 = 9\\ 4x^2 + 4x + 1 = 9\\ 4x^2 + 4x + 5 = 13$



Очень много примеров, которые органично приводят к решению уравнения через полные квадраты. Потом уже можно вводить дискриминант (как простой алгоритм для решения уравнений, когда ученики устанут выделять полные квадраты), и Виет с четным дискриминантом как «ноу-хау».

Схожий подход используется в учебниках. Увы, не во всех. И не везде видна четкая последовательность. По слухам, некоторые авторы теряли листы черновиков в трамваях, а потом заменяли утерянные куски выражениями вроде «легко показать, что...». В итоге, вместо спокойных прыжков с примера на пример, студенты были вынуждены перепрыгивать через пропасть. Сколько людей сорвалось и еще сорвется за 10+6 лет обучения в школе/ВУЗе?

Личный пример (просили в оригинальном посте). На первом курсе матана я страдал. Спокойно решая примеры, совершенно не усваивал теорию. Попросил однокурсника о помощи с вычислением длины кривой через интеграл. Тот взял бутылку пива, нарисовал рандомную кривую, спрямил бесконечно малыми отрезками, выделил один такой отрезок, достроил его до треугольника dl, dx, dy, и спросил: «Теорему Пифагора помнишь»? Дальше все было просто.



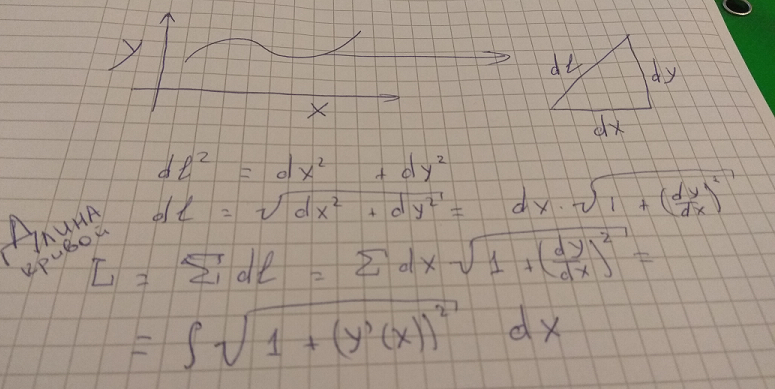
Я его спросил: а почему такое не показывают на парах/в учебниках? Он показал пару контрпримеров, объяснил зачем нужен формализм в матане — и у меня попёрло. Я просто читал теорему, выделял главное, писал/решал тривиальные примеры, потом разбирался с формализмом — и реально понимал, о чем идет речь.

Я не знаю, можно ли массово использовать подход общий обзор => контрпримеры => формализм. Не знаю, сколько и какой теории/практики нужно набрать студенту до «прорыва», с трудом представляю себе, как ставить педагогические эксперименты на эту тему, и сколько труда придется вложить в исследования. Но память о том объяснении живет уже 10 лет. И спустя все эти годы я стараюсь слушателям сначала дать общую картину, потом показать проблемы, и потом уже погружаться в детали.

Вы скажете, мои персональные ощущения могут быть ошибочными. Помимо них у меня есть только аналогичные идеи от Хэмминга:
… я мог изучать, какие методы были эффективны, а какие нет. Посещая встречи, я уже изучал, почему некоторые работы запоминают, а большинство – нет. Технический человек хочет дать очень ограниченную техническую лекцию. Как правило, аудитория хочет широкую лекцию общего характера и хочет гораздо больше общего обзора и введений, чем желает дать спикер. В результате многие лекции неэффективны. Лектор называет тему и внезапно ныряет в детали. Мало кто может уследить. Вы должны нарисовать общую картину, чтобы рассказать, почему это важно, и затем медленно развернуть эскиз того, что было сделано. Тогда большее число людей скажут: «Да, Джо сделал это» или «Мэри сделала то, я действительно вижу, о чём это. Да, Мэри дала по-настоящему хорошую лекцию, я понимаю, что она сделала». Как правило же, люди дают очень ограниченную, безопасную лекцию; это обычно неэффективно. Кроме того, многие лекции переполнены информацией…

Идеи россыпью

Должен заметить, мой опыт в преподавании крайне ограничен. Возможно, вы заметили, что я ограничился школьной программой и матанализом. Увы, это те области, где у меня была возможность соприкоснуть теорию с практикой. Я до сих пор не понимаю сути определителя в алгебре, не осознаю проективную геометрию, и лишь полгода назад начал проникаться матрицами (сразу после практики, ага). Неплохая иллюстрация поговорки «теория без практики мертва».

Как мне рассказывали, в НМУ новый концепт всегда вводился с десятком вопросов. А что если так? А если этот пункт условия не выполнен? Что нужно, чтоб дополнить наш концепт до полугруппы? Слушателям давали поиграть с предметом. Привыкнуть. Думаю, над опытом НМУ стоит хорошенько задуматься.

Наверняка в высших разделах математики подход «сначала пример, потом абстракция» не сработает. Так, примеры «на бумажке» никак не помогают осознать RSA. Зато растущее время работы программы с увеличением длины ключа помогает прочувствовать чисто практические аспекты.

Есть опасение, что «идеальные/тепличные» школьные учебники приведут к шоку при работе с «вышкой». Вроде как, «хардкорщика надо воспитывать смолоду».

Довольно сложно разрабатывать курсы, надеясь что студенты уже что-то знают. Чем больше требуемая база, тем больше вероятность, что что-то из базы студентом недопонято.

Говорят, пик формы математиков — 30 лет. После 30 уже можно нагружать их писать учебники, дав в напарники спеца методиста.

Текущие технологии позволяют писать тексты командой, используя git. На хабре недавно проскакивала статья про компиляцию TeXa в pdf в процессе CI. Уверен, авторский коллектив с хорошим инструментарием может писать гораздо более качественные учебники.

Помимо профессоров, учителей, студентов и школьников в математике есть государства. И регламенты. И требования. И сертификации. Все это влияет на учебники, авторов, преподавателей, и качество подачи материала.

Как можно улучшить подачу материала в математических текстах


В текущих (российских) реалиях — никак. Энтузиасты есть, профессионалы есть, мотивации нет.

У профессоров математики хватает своих задач, чтобы писать учебники. Иногда не хватает чисто гуманитарных скиллов, писать книги в университетах не учат. Плюс, профессиональная деформация: «очевидное» для профессора может быть неподъёмно для студентов. Учителя математики загружены текучкой. И бумагами. И репетиторством. Про государство промолчу. Почти не сталкивался с его представителями, так что говорить нечего. Разве что, упомяну политику замену учебников каждые три года. После школы я хотел сдать свои учебники в библиотеку, мне сказали «они старые, нельзя их хранить». Мотивации писать хорошие учебники такой подход не добавляет.

Иными словами, от системы образования лично я позитивных подвижек не жду. Надеюсь, конечно, но не жду. Что выручает — проблески ИТ и прочей инженерии. На одной из математических конференций я получил от одного из участников книгу по компьютерной графике. Автор работал в конторе, разрабатывающей графическое ядро какой-то чертежной системы, и материал был вполне неплох. Математика была не «чистая», прикладная, но сам факт существования хорошего учебного материала безусловно радует.

Еще один подход: преподаватели от компаний, работающие в ВУЗах. Математических текстов от этих ребят ждать не приходится, специфика не та. Разве что, геймдевщики соберутся написать мануал по теорверу, или графики напишут про алгебру/геометрию необходимую для разработки тех же САПРов (если такие проекты есть — зовите).

Наконец, есть различные негосударственные образовательные платформы, вроде той же Coursera. Эти ребята могут все, ибо работают за деньги, конкурируют, быстро получают обратную связь. Но у них свой недостаток: формат подачи данных иной. Непосредственно текстов они не пишут.

И к чему все придет в будущем?


Самому интересно. Может, всё останется как есть. Может, будет уход от текстов в математике. А может, авторы проникнутся идеей "продукт текст должен быть удобным для клиента читателя", и силами первопроходцев удастся таки переломить традицию. Тогда лет через 30-50-100 у нас появятся учебники, понятные большинству читателей.

Upd1. Вставил фото с вычислением длины участка кривой.

Upd2. В комментариях часто упоминают, что текст посвящен проблемам преподавания, а не профессиональной математике. Причина проста: большая часть виденных мною «профессиональных» работ в плане подачи материала не отличается от учебников. При этом, школьная\университетская литература известна большинству на хабре, а «профессиональная» — процентам.

Комментарии (330)


  1. basilbasilbasil
    08.11.2018 21:53
    #19341818
    +6

    Или каждый интересующийся возьмёт одну тему и аналогично согласно схеме опишет. Сначала неидеально, потом доточат


    1. DSolodukhin
      09.11.2018 00:59
      #19342476
      +4

      И получится Википедия.


      1. Mladolaborant
        09.11.2018 01:36
        #19342578
        +17

        Не получится.
        На википедии вначале выпилят то что вы запостите за ОРИСС, а потом заменят на цитату из Брокгауза-Эфрона, разбавив вставками из БСЭ о том, как хорошо предмет статьи влияет на удои озимых и подтверждает верность учения Ленина-Сталина.


        1. Aingis
          09.11.2018 12:45
          #19344154

          Вы путаете ОРИСС и научно-популярную подачу материала. Первое вне правил, а последнее приветствуется и рекомендуется. Если у вас в результате подачи не получается внезапных результатов, которые не подтверждаются источниками, то это не орисс. Но писать надо грамотно и со ссылками, да.


          1. tangro
            09.11.2018 13:07
            #19344292
            +4

            последнее приветствуется и рекомендуется

            У Вас какая-то своя особенная википедия? Потому что в обычной пока ты текст не приведёшь к виду неудобочитаемого нудного бубнения — его не примут.


            1. Aingis
              09.11.2018 13:45
              #19344454
              -3

              А вы правила читали?

              «…Статья должна быть написана в научном, но доступном (т. н. научно-популярном) стиле. Следует избегать канцелярита и подобных ему искусственных словесных построений. Писать следует просто и внятно…»
              И да, в Википедии никто не «принимает» текст. Как написали — так и будет висеть, если правки не откатят по каким-то весомым причинам (вандализм, явные противоречия и тому подобное), или не отредактирует другой участник. Максимум есть «проверенные версии».

              И, что характерно, вы не привели ссылок на требования «приведения к виду неудобочитаемого нудного бубнения». Не удивлюсь, если окажется что вы что-то недопоняли, написали что-то не совсем корректно, или что-нибудь в таком роде. В конце концов Википедия — это сообщество. Надо договариваться. Содержание энциклопедии — результат консенсуса.


              1. gremlin244
                09.11.2018 15:12
                #19344954
                +5

                Вы конечно извините, но научно-популярным на вики и не пахнет. В моем понимании, по всей видимости отличном от вашего, научно-популярное означает, что рандомный человек с минимальной теоретической подготовкой зайдя на страницу сможет хотя бы чуть-чуть понять смысл термина, а не утонуть в других терминах и гиперссылках. Да собственно по вашей ссылке примерно это и написано. Но стоит чуть дальше какого-нибудь умножения зайти, и вики уже предполагает что ты знаешь кучу всего остального. Это понятная проблема, точнее я даже не уверен что это проблема, все же максимально полно изложить суть на мой взгляд чуть более важно, но говорить что вики пишется в научно-популярном стиле такое себе.


                1. khim
                  09.11.2018 16:47
                  #19345492
                  +1

                  Дурацкий вопрос — а вы английскую Википедию пробовали читать?

                  Там всё гораздо удобнее: неформальное описание, понятное человеку с улицы — в первой паре абзацев, дальше содержание, а уж под ним — подробный текст, который уже может требовать специальных знаний.

                  Русская тоже потихоньку от стиля «всё очень точно, но неподготовленный человек может застрелиться при попытке это понять» отходить начинает. Хоть и мееедленно-мееедленно.


                  1. 0xd34df00d
                    09.11.2018 17:32
                    #19345692

                    Дурацкий вопрос — а вы английскую Википедию пробовали читать?

                    Зашёл сходу на https://en.wikipedia.org/wiki/Parametricity. Ну так себе. https://en.wikipedia.org/wiki/System_F. Неформально, ага.


                    Да что там эта ерунда ненужная. Давайте возьмём что-то более распространённое, например, https://en.wikipedia.org/wiki/Cholesky_decomposition. Тоже всё интуитивно и неформально?


                    1. mao_zvezdun
                      09.11.2018 19:02
                      #19346118

                      Даже среди этих статей две не хуже русской версии, а третью вообще на русский не перевели еще. Но ведь в целом английские варианты действительно более удобочитаемые. У меня вот немного другой «сходу» получился, я ткнул в «Дискриминант», раз уж он поминался в постинге. В английский статье самые первые строчки мне показались понятнее. Там ведь правда сначала в первом же предложении в двух словах дается и понятное определение и пример какая от дискриминанта может быть польза.


                    1. khim
                      09.11.2018 19:38
                      #19346244

                      Давайте возьмём что-то более распространённое, например, en.wikipedia.org/wiki/Cholesky_decomposition. Тоже всё интуитивно и неформально?
                      На все «сложные» термины есть ссылки, там же написано — зачем это нужно, есть ссылка на первооткрывателя, то есть фактически прочитав один этот абзац — вы можете удовлетворить своё любопытство.

                      То, что не всего понятия вырадаются через совсем уж интуитувно понятные… ну тут уж так математика устроена.

                      Сравните с тем, что в русской версии: теста в преамбуле, до «содержания», больше, но при этом полезной информации меньше. Написано как это понятие можно ещё больше обобщить, а нафига так делать — вообще непонятно.

                      Понятно только вы дочитаете-таки статью до конца и доберётесь до раздела «приложения» и там, где-то посреди этого раздела увидите-таки ответ свой жгучий вопрос «а на&&я?».

                      По-момему вполне хорошее подтверждение и моего тезиса и всего того, что топикстартер написал.


                1. Aingis
                  10.11.2018 11:14
                  #19347880

                  «Вы конечно извините, но научно-популярным на вики и не пахнет.»
                  Так потому и не пахнет, что никто не пишет, распространяя чушь про то, что «признают ориссом», не удосужившись понять даже, что такое «орисс». Критиковать все могут, но хоть бы кто из таких критиков свой сколь-либо значимый вклад сделал.

                  Как-то нелогично сначала отпугивать потенциальных участников от написания, а потом ныть, что никто толком не написал, не находите?


                  1. Aingis
                    10.11.2018 12:19
                    #19348024

                    Стоит ещё добавить, что у фонда «Викимедиа РУ» не всё так просто с финансированием. По закону об «иностранных агентах» они не могут получать деньги из-за рубежа (то есть от международного фонда, куда идут пожертвования), и живут на то, что соберут внутри страны. А ведь именно фонд занимается привлечением новых авторов, обучением и т.п. Поэтому, кстати, и в русской Википедии больше нет баннеров с Джимми Уэйлсом.


            1. nafgne
              09.11.2018 21:17
              #19346564
              -4

              Ну идите на лурк и там читайте, если скучно.


              1. saboteur_kiev
                10.11.2018 01:51
                #19347316
                +1

                Зря вы так про лурк. Некоторые статьи там раскрывают суть гораздо лучше, чем Вики. Я имею ввиду именно статьи про некоторые термины и научные теории. Просто их там слишком мало.


          1. ganqqwerty
            09.11.2018 17:17
            #19345632
            +5

            Совершенно ужасающие в нашей Википедии тексты по математике.


            1. IvanTamerlan
              09.11.2018 22:30
              #19346840
              +1

              Как кто-то шутил про один учебник в техникуме(!):
              «Один профессор создал напоминание для другого профессора, который немного подзабыл»
              Этот неловкий момент, когда раздобыл советский учебник и там понятнее изложено, чем в десятках современных и местами даже актуальнее(sic!). Актуальность достигается тем, что понятия до сих пор не устарели и более полно развернуты. У современных авторов — пропали целые разделы, зато вместо них — вода, идентичная натуральной. Максимум, что из современного учебника полезного — обзор новейших технологий.
              Если что — учебник, связанный с прикладной математикой. Утерян сразу после сессии.
              Еще можно упомянуть в качестве образца Детскую энциклопедию, эдакая доступная версия Википедии на десятилетия раньше.


      1. c0f04
        09.11.2018 07:30
        #19343062

        Викиучебники:
        ru.wikibooks.org/wiki/Заглавная_страница

        Это один из проектов википедии. Сама Википедия — это энциклопедия, а не обучающие материалы. Например, из викиучебника про квадратные уравнения:
        ru.wikibooks.org/wiki/Основы_алгебры/Квадратные_уравнения


        1. namikiri
          09.11.2018 11:52
          #19343860
          +1

          Есть ещё MathProfi, который действительно понятно всё расписывает, человеческим языком, но без потери смысла.


        1. tangro
          09.11.2018 13:06
          #19344282
          +1

          И что, хороший учебник типа? Всё то же самое о чём пишет автор: отсутствие введения, цели, основы, примеров.


          1. ganqqwerty
            09.11.2018 17:20
            #19345646
            +2

            там меньше народа, поэтому если вы напишите что-то понятное и по делу меньше вероятности будет, что набежит куча коллег-викоидов и все попортит


  1. akhalat
    08.11.2018 22:00
    #19341852
    +7

    Какие потребности, какой математики, чем не устраивают рациональные — да пес его знает

    зачём вы вводите в заблуждение с самого начала, уж и Фихтенгольца (в отличие от многих других) всё это разжевывается на первой странице — невозможность извлечения квадратных корней, и как пример: ненаходимость диагонали единичного квадрата

    на самом деле, единственная проблема в том, что «матан» ставят в учебные планы тех специальностей, которым он на таком уровне не нужен. это действительно проблема наших реалий, на западе это решается наличием курсов на выбор и совсем упрощенными курсами типа calculus где всё объясняется на пальцах

    P.S.:
    По слухам, некоторые авторы теряли листы черновиков в трамваях, а потом заменяли утерянные куски выражениями вроде «легко показать, что...»

    не некоторые авторы, а Лифшиц (ибо, как известно, Ландау ничего сам не писал). но это вообще про физиков-теоретиков, к математике этот фольклор приплетать не надо, у них там была «своя атмсофера»


    1. Oxoron Автор
      08.11.2018 22:29
      #19341994
      +3

      уж и фихтенгольца (в отличие от многих других) всё это разжевывается на первой странице

      Мой косяк, спасибо, что указали. Вы абсолютно правы, разжевывается и про корень, и про корни.
      К сожалению, пример с пределами по-прежнему актуален. Сам предел вводится, его назначение непонятно.


      1. akhalat
        08.11.2018 22:37
        #19342028
        +5

        с глобальной точки зрения пределы нужны потому что весь «матан» — это учение о бесконечно малых, строго и корректно это понятие можно определить лишь с помощью предела

        с практической точки зрения, фихтенгольц в том же параграфе извернулся и уже придумал для вас примеры как с помощью пределов можно считать площади и объемы

        вообще, фихтенгольц — это простейшая книга по матану, где всё разжёвывается до мелочей и читателя просто закидывают разнообразными примерами, настолько приближенными к практике, насколько это возможно


        1. Oxoron Автор
          08.11.2018 23:23
          #19342182
          +3

          Увы. При подготовке статьи я выкинул из нее пару абзацев критики примеров к тому же пределу последовательности. Если желаете — можем обсудить в личке.

          Я не спорю, Фихтенгольц хорош, но вы взгляните на учебник глазами рядового студента. На одной странице выделены курсивом понятия величина, переменная, постоянная, множество, направленная переменная, предел, последовательность, и еще пару незначительных. Примеры только в конце главы, до них еще дочитать надо. Приходится или вдумываться, или пролистывать с мыслью «да вроде все ясно». Мотивации введения термина Предел — сноска на дополнение.

          Можно же было перестроить порядок подачи материала, дать несколько примеров последовательности с самого начала. Потом уже пояснить, зачем нужен предел, или просто указать на его существование, вычислить предел для последовательностей из примеров.

          Что самое интересное, Фихтенгольц приблизительно это и делает: упоминает прогрессии, окружности, корни — что-то уже знакомое читателю. Верные вещи делаются в неверном порядке.


          1. akhalat
            08.11.2018 23:50
            #19342294
            +6

            по вашему выходит, вас автор постоянно должен уговаривать прочитать очередную главу его учебника, притом ещё и (ужас!) до конца. в то, что автор неспроста вставил в книгу какие-то определения и понятия с пониманием своего дела, и их важность откроется по ходу дальнейшего изучения — вы верить отказываетесь упорно, вам нужны «подтверждения» здесь и сразу, причём непременно сразу после каждого вновь вводимого определения. эдакая «морковка», которой надо постоянно завлекать

            вот здесь постоянно звучит слово «мотивация» — это на самом деле какое-то детсадовское требование. предполагается, что если человек решил изучать анализ, то пресловутая мотивация у него уже есть. если это делается из под палки, то настоящая проблема в том, зачем человека насилуют этим «матаном», а не в том, что современная математическая запись «неправильная» или учебники «плохие».

            Приходится или вдумываться

            действительно, какой ужас, читая серьезную научную литературу приходится обдумывать прочитанное

            Мотивации введения термина Предел — сноска на дополнение.

            в дополнении излагается «Общая точка зрения» на предел, как там написано, а не какая-то «мотивация». как вы можете предположить «общая точка зрения» будет ещё более абстрактней, чем простейшее школьное определение предела, данное в начальной главе


            1. Oxoron Автор
              09.11.2018 01:09
              #19342514
              +3

              Именно морковка. Именно подтверждения здесь и сейчас. В идеале — зацепки на уже изученные кусочки. Для читателя — идеальные условия.

              Упростились тексты — сэкономилось время читателей. Больше читателей дочитало книгу. Больше читателей поняло книгу. В случае матана больше студентов не восприняло матан как насилие.

              Да, не всегда у автора есть ресурсы на упрощение. Но если имеется возможность упростить материал — стоит ли ею пренебрегать?


              1. akhalat
                09.11.2018 01:16
                #19342528
                +3

                Вы понимаете, что если перед каждым определением давать список каких-то «мотиваций», то это НЕ упростит понимание — это просто замусорит текст, неоправданно удлинит книгу, а действительно важные вещи просто потонут в «воде». Если что-то непонятно, то надо перечитывать и обдумывать прочитанное — по другому, к сожалению, процесс обучения не работает. Всё равно непонятно — задавать вопросы лектору. Если лектор не хочет идти на контакт и объяснять — это плохо, это уже другая проблема. Вы подошли к одногруппнику и он вам объяснил — тоже отличный способ.

                И, уж придётся вам мне на слово поверить, но из всех курсов матанализа — Фихтенгольц самый простой и самый доступный, и содержит больше всего наглядных примеров и приложений. Этим объясняется, кстати, его довольно внушительный объем (2000 страниц трех томов). Правда, есть ещё Пискунов, но он больше позиционируется как для втузов, но на самом деле не для углубленного изучения — это отличный выбор.


                1. saboteur_kiev
                  09.11.2018 01:48
                  #19342604
                  +6

                  По-другому процесс обучения работает.

                  Очень часто ситуация, когда нужно просто понять смысл определения. И в попытках понять ты читаешь определение, состоящее из кучи формальных слов, из которых тебе непонятно примерно 50%.

                  При этом, когда ты продолбился головой об стену, порешал практические задачи, потратил на это месяц-другой и наконец понял, ты сам можешь выдать определение, состоящее из обычных народных слов, которых тебе не хватало месяца два назад.

                  Тратить каждый раз по месяцу на каждый новый математический термин — могут себе позволить только математики. В жизни не всегда нужно знать всю математику, очень много айтишников работают в смежных темах, когда нужно немного копнуть.
                  К сожалению именно с математикой «немного» практически никогда не выходит.


                  1. akhalat
                    09.11.2018 02:04
                    #19342630
                    +3

                    По-другому процесс обучения работает.

                    обучения чему: науке или ремеслу? если науке, а конкретно матанализу, то он работает именно как я описал. учитывая, конечно, что у вас ещё будут лекции и семинары, где можно и надо задавать вопросы

                    В жизни не всегда нужно знать всю математику, очень много айтишников работают в смежных темах

                    так не зря здесь есть комментарии, что проблема больше в самой организации процесса высшего образования как целого у нас. в других странах, например, насильно матаном никто не пичкает: вы сами выбираете какие предметы слушать (но если не прослушан матан, то предметы, требующие его брать нельзя, и естественно он всё равно будет обязателен если вы поступили на математика или естественника), для не-математиков есть облегченные варианты, называемые calculus («вычисления») гдё всё просто и наглядно, «обычным народным» языком, и где вас научат решать типовые задачи. но сделать шаг в сторону после такого вы всё равно не сможете, т.к. вас просто «натаскают» на типовые примеры, без понимания самой сути теории

                    Тратить каждый раз по месяцу на каждый новый математический термин — могут себе позволить только математики

                    не надо преувеличивать. если учить матан последовательно и постепенно, то каждый термин будет вам уже знаком, останется понять как они сочетаются вместе для генерации нового определения
                    К сожалению именно с математикой «немного» практически никогда не выходит.

                    вот вы точно отобразили суть математики. там всё последовательно и строго, каждый следующий шаг должен вытекать из предыдущего, если отсутствует хоть одно промежуточное звено — рушится вся логическая цепочка, так что брать «с наскока» не получится


                    1. Shtucer
                      09.11.2018 09:06
                      #19343222
                      +2

                      У меня такое ощущение, что вы обсуждаете разное. Один говорит: учебник хорош. А второй: а мне хотелось бы самоучитель!
                      Все эти "морковки", "тычинки" и "пестики", вполне могут быть выданы преподавателем. У меня так было. Учебник был скорее как справочник и дополнительные материалы. Интересная лекция мотивирует раз в M, а то и в N, раз лучше любого учебника, даже если он с картинками и "разговорами".
                      Но, тут я соглашусь: хороших лекторов наплодить, наверное, я не уверен, сложнее, чем написать один сферический всем понятный учебник.


                      1. DaneSoul
                        09.11.2018 19:14
                        #19346172

                        УЧЕБНИК и должен работать как самоучитель, роль преподавателя помочь освоить учебник и если без преподавателя его освоить не возможно — это очень плохой учебник! Это я Вам говорю как человек, который очень много занимался именно самообразованием.
                        А справочник — это справочник, у него совсем другая структура и задачи, вот он именно дополнительные материалы.


                        1. Shtucer
                          09.11.2018 19:24
                          #19346208
                          +1

                          УЧЕБНИК не обязан работать как самоучитель, для самообразования он, как бы, в том числе. По определению. В то время, как самоучитель — это УЧЕБНИК для самостоятельного обучения. И нет, я не отрицаю, что кому-то лекции дополняют учебник, а кому-то наоборот. Самообразование же не отрицает возможность слушать лекции?


                          1. IvanTamerlan
                            09.11.2018 22:37
                            #19346870

                            самоучитель — это УЧЕБНИК для самостоятельного обучения

                            Следует ли из этого определение:
                            учебник — это книга для несамостоятельного обучения

                            ?
                            И воображение рисует инвалидов, которые не способны все делать самостоятельно и должны полагаться на постороннюю помощь, причем эта помощь будет очень дорогой в современном мире. В данном случае — расходы на репетиторов или преподавателей.


                            1. Shtucer
                              09.11.2018 22:59
                              #19346936

                              Попробуйте напрячь своё воображение ещё немного, и представить систему образования всю. Целиком. И подумайте над тем, что это вообще такое "система образования" и для чего вообще нужно это, якобы никому ненужное, наставничество.


                              1. IvanTamerlan
                                09.11.2018 23:49
                                #19347092

                                Это несложно, т.к. ответ был заранее готов. «Древо технологий» аналогичная игровым, хотя такая структура в реальности больше похожа на сеть и очень сложную. Но сети две — система знаний (обычный ориентированный граф) и система образования (граф, имеющий направления и начальную точку). Система знаний — такая сеть, работа с которой требует уже наличие знаний. Система образования — это такая сеть, у которой есть некоторый «вход», который не требует знаний.
                                У современной системы образования есть недостаток — она не представлена в таком виде, отсюда проблема в виде «потерь входов» и прочие проблемы, затронутые в статье. А вот простые системы знаний иногда даже можно увидеть — хотя бы граф связей станиц Википедии, но более сложные системы знаний все таки разрознены.


                            1. Shtucer
                              09.11.2018 23:16
                              #19346990

                              Следует ли из этого определение:

                              Нет, не следует:
                              Учебник — это книга для обучения, в том числе самостоятельного.


                        1. Druu
                          09.11.2018 21:22
                          #19346586

                          УЧЕБНИК и должен работать как самоучитель, роль преподавателя помочь освоить учебник и если без преподавателя его освоить не возможно — это очень плохой учебник!

                          Так учебник надо осваивать, а не прочитал и "ой, чот непонятно".


                        1. saboteur_kiev
                          10.11.2018 01:52
                          #19347318
                          +1

                          А тут где-то в камментах говорят, что препод, вместо того, чтобы объяснить, говорит «иди читай учебники».


                    1. Hardcoin
                      09.11.2018 12:34
                      #19344090
                      +5

                      он работает именно как я описал

                      Да, как вы описали, он работает. Но вы никак не обосновали, что этот способ лучший. Последовательность и строгость никак не противоречат учёту особенностей человеческого мышления. И понять от частного (от примеров и потребностей) к общему намного проще, чем от определения к частностям.


                      Кстати, это результат исследований, что люди строят абстракции по примерам намного проще, чем факты по абстракциям.


                      1. akhalat
                        09.11.2018 15:02
                        #19344880

                        учёту особенностей человеческого мышления.


                        это хорошо, что вы отметили, что принятый в математике способ мышления отличается от обыденного. и одной из задач курса матана, как элементарнейшего введения в математику, в том числе и состоит в обучении этому способу мышления. так как если не понять его на простом курсе матана, где для каждого понятия можно подобрать осязаемый пример, то с воспритие дальнейших более продвинутых разделов станет и вовсе невозможным, ибо там уровень абстракции будет уже другой


                        1. Hardcoin
                          09.11.2018 15:10
                          #19344934
                          +2

                          вы отметили, что принятый в математике способ мышления отличается от обыденного

                          Не приписывайте, пожалуйста. Это вообще никакого отношения к моему комментарию не имеет.


                          Сожалею, что не смог донести мысль. Нужно отделять результат (например, понимание математики) и способ получения результата. Ваша неявная позиция, что текущий способ — единственно верный для получения нужного результата, а при других способах результат не будет достигнут — не имеет под собой оснований.


                          Я говорил именно про способ достижения. Способ должен лучше учитывать особенности мышления. Он и сейчас немного учитывает — и у Фихтенгольца есть примеры — но можно учитывать лучше.


                          1. akhalat
                            10.11.2018 04:19
                            #19347456

                            потому что в математике важно понимать формулировки исходя только из внутренней логики теории. это важно, т.к. в более продвинутых разделах многие понятия уже будет не так просто соотнести с простыми физическими или геометрическими приложениями «на пальцах». та же теорема Ферма (великая) формулируется элементарно, но доказывается через сверх-абстрактные конструкции

                            вы читаете определение, пытаетесь его обдумать в рамках уже известных вам определений и формализма, затем переходите к примерах (которые у Фихтенгольца зачастую идут сразу после того, как дано определение — буквально несколькими строчками ниже), на которых наглядно показывается как определение работает и почему оно сформулированно именно так. и, да, это нормально — читать и перечитывать материал несколько раз и вдумываться в него, пока путём тренировки не придёт понимание формализма и соответствующего способа мышления

                            понимание формализма вам в любом случае нужно, если вы собираетесь быть математиком или профессионально использовать математику в своей работе. если — нет, то как я уже неоднократно говорил, именно для таких целей были придуманы курсы на выбор и облегченные варианты типа calculus — то, что у нас такого нет, это уже разговор о недостатках системы образования в целом. но Фихтенгольц — это именно учебник по анализу с математической степенью строгости

                            Забавно, если так учили бы плаванию. Расскажут немного теории, а потом столкнут с обрыва и вперед

                            так было бы, если бы вам в институте преподаватель прочитал вводную лекцию, потом сказал — всё, встречаемся на экзамене в конце года, сидите читайте учебник, что не поняли — это ваши проблемы, спрашивать буду по всей строгости, не сдадите — вылетаете из института. так нет же, вам минимум раз в неделю читают лекции и проводят семинары, на каждом из которых можно и нужно задавать вопросы


                        1. IvanTamerlan
                          09.11.2018 22:42
                          #19346892

                          Забавно, если так учили бы плаванию. Расскажут немного теории, а потом столкнут с обрыва и вперед

                          в обучении этому способу мышления

                          Никто не умирает на уроках матана, поэтому и попыток что-то поменять не предпринимают в лучших традициях «Пока гром не грянет — стиль преподавания не изменится».


                  1. Druu
                    09.11.2018 09:56
                    #19343364
                    +4

                    Очень часто ситуация, когда нужно просто понять смысл определения.

                    Невозможно понять смысл определения для абстрактного объекта, просто его прочитав, как бы он ни был записан и разъяснен.


                    Представьте себе человека, который никогда не видел жидкостей и не представляет, что это такое. Как бы вы ему ни объясняли, как она себя ведет, и что представляет — он все равно не поймет. Это невозможно. У него нет соответствующего житейского опыта, который позволяет вам с легкостью, даже не задумываясь, ответить на вопрос: "в стакане налита вода, стакан переворачиваем, что будет?". Точно так же не существует житейского опыта, который бы вам помог понять, что такое кольцо или поле (а это совершенно базовые объекты, чего уж о том, что сложнее, говорить). Единственный способ — нарабатывать этот опыт в мысленных экспериментах.


                    Или на это можете взглянуть с другой стороны — вот тот же е-д формализм, это просто определенный язык, который вам позволяет рассуждать о бесконечно малых величинах и непрерывности. Можно ли изучить язык, просто почитав какие-то объяснения? Конечно, нет! Нужна полноценная речевая практика и никак иначе. Без практики вы понимать язык не начнете, не бывает так.


                    По-этому в учебниках никто не ставит себе целью "объяснить так, чтобы стало понятно" — это было бы просто глупостью, подобная задача неразрешима. Учебник должен предоставить достаточно точное и полное объяснение, чтобы студент потом мог по нему ставить мысленные эксперименты и, с-но, показать, как эти эксперименты следует ставить (на примере доказываемых теорем, например). А дальше дело за практикой. Именно по-этому у вас "через пару месяцев решения задачек", после наработки ассоциативных связей, и появляется понимание.


                  1. mayorovp
                    09.11.2018 10:19
                    #19343412

                    И в попытках понять ты читаешь определение, состоящее из кучи формальных слов, из которых тебе непонятно примерно 50%.

                    Это всего лишь означает, что нужно сначала понять эти самые непонятные слова, а потом возвращаться к определению.


                    1. IvanTamerlan
                      09.11.2018 22:50
                      #19346918

                      математика — куча заимствований и куча непонятных слов. По сути — это больше иностранный язык (специализированный, профильный). Но никто не учит его как иностранный язык, в том числе с созданием словарей. Особенно, когда некоторые понятия могут встречаться единожды, тогда смысл запоминать и понимать, если достаточно словаря с разъяснением конкретного термина. Без разъяснения мы упускаем всё то, где этот термин встречается, а в университете таких текстов огромное количество и студенты пользуются заглушками или пустышками для этих терминов, что иногда нарушает всю логику, приводя не к пониманию, а к зубрежке.


                      1. khim
                        09.11.2018 23:32
                        #19347036

                        Но никто не учит его как иностранный язык, в том числе с созданием словарей
                        Вы никогда не видели Бронштейнa и Семендяева? Мне достался от отца. Не помню какое издаение, но знаю что давно. Всё очень понятно и подробно написано.

                        Без разъяснения мы упускаем всё то, где этот термин встречается, а в университете таких текстов огромное количество и студенты пользуются заглушками или пустышками для этих терминов, что иногда нарушает всю логику, приводя не к пониманию, а к зубрежке.
                        А тут больше вина школьного образования. Которое приучает людей думать, что у учителей есть задача их чему-то там научить. Нету. Учителя — помогают вам научиться, но если вы хотите потратить пять-шесть лет впостую и уйти с пустой головой… это ваше личное дело.

                        Самая большая проблема нашего образования не в том, как устроены учебники, а в банальном отсуствии двоек в школе и большими проблемами с ними в ВУЗе. В результате людей приучают к тому, что знания не нужны, нужно как-нибудь троечку выциганить…


                        1. IvanTamerlan
                          10.11.2018 00:09
                          #19347156

                          К сожалению, не был знаком с «Бронштейнa и Семендяева».

                          Про школьное образование — тут очень много проблем:
                          — подбор коллектива (случайны процесс, причем с негативным отбором, т.к. успехи не поощряются и иногда ставятся даже в вину, типа "не спеши, коллектив не успевает")
                          — мотивации в виде «зачем учимся?»
                          — школьное образование запрещает самостоятельно думать, т.е. не пытайся сам делать, а делай как учитель и думай как учитель

                          Замечания: в ВУЗе нет учителей, 5-6 лет относится скорее к ВУЗу, но школьные 9-11 лет тоже могут потратить время в пустую и человек уйдет с пустой головой. Это еще в лучшем случае!

                          Отсутствие двоек? Вы серьезно? Даже в советском образовании были двойки и люди выцыганивали тройки, хоть это было тогда и сложнее. Тогда приучали к нужности образования! В результате работал на гос.предприятии и люди с советским образованием были иной раз очень большой проблемой — трудности в переквалификации и «всегда так делал» (даже если это не правильно). При кривизну рук советских сантехников и даже инженеров (особенно из автопрома) — ходили легенды.

                          Также из недостатков советского образования (современного и подавно):
                          — проблема мотивации, особенно зачем учить, если можно зазубрить в ночь перед экзаменом
                          — социализация людей и сексуальное воспитание (правильный подбор партнера, психология, курсы для родителей, организация групп и т.д.) — поставлено на самотек и «авось»
                          — финансовый менеджмент (как распоряжаться деньгами — накопление, инвестирование и т.д.) — в советское время табу, сейчас — просто игнор. И многие придумывают варианты на тему «Надо пропить!»
                          — скорость обучения. У всех разная, но всех под одну скорость, в итоге медлительные отстают, а быстросхватывающим — унижения
                          и т.д.
                          Я привел лишь часть проблем. Может, не в двойках дело? Перечисленные проблемы в большинстве случаев даже другие действующие и старые системы не решают.


                          1. khim
                            10.11.2018 02:03
                            #19347328

                            Отсутствие двоек? Вы серьезно? Даже в советском образовании были двойки и люди выцыганивали тройки, хоть это было тогда и сложнее.
                            Даже в советском образовании люди получали диплом об окончании 8го (а кто и 10го класса) с пометками «удовлетворительно» (и выше) во всех графах обладая при этом знаниями на уровне начальной школы.

                            Я ровно это и имею в виду. Нет двоек — это не обозначает, что их не ставят. Это обозначает, что есть целая система, которая заставляет учащихся и учителей ставить, в конце-концов, тройку «за красивые глаза». За годы обучения в школе человек сознательно или не сознательно подводится к выводу о том, что его задача — не научиться что-то делать, а «выцыганить» тройку.

                            Перечисленные проблемы в большинстве случаев даже другие действующие и старые системы не решают.
                            Проблема мотивации, как минимум, напрямую зависит от феномена отсуствия двоек. Если система, так или иначе, не допускает появления людей, которые получили неуд (за то, что у них реально нет знаний), то отсюда и получается зубрёжка в ночь перед экзаменом и прочее. То же самое со скоростью обучения: если у вас нет возможности разделить людей на быстро обучаемых и медленно обучаемых, а главное, нельзя вынести «за скобки» совсем необучаемых (неважно — не могут они обучаться или не хотят), то отсюда возникают запреты за самостоятельное мышление и прочее — потому что для педагага не очеь важно, сколько людей научатся что-то делать хорошо — зато черезвычайно важно не допустить, чтобы кто-то «отпал совсем».

                            Ну это всё равно как если бы вас заставили мясо варить, не давая снять пену и выкинуть её. В результате будет получен большой котёл… «мутной хрени». Вместо прозрачного бульона.


                            1. IvanTamerlan
                              10.11.2018 13:03
                              #19348142
                              -1

                              Тут скорее проблема отсутствия реального и осознаваемого наказания, нежели эфемерные двойки, которые сами по себе наказанием не являются.
                              Под осознаваемым наказанием — здесь и сейчас, а не когда-нибудь с кучей условностей.

                              Проще на RPG объяснить. Если персонажу поставить дебаф (метка об получении со временем отрицательного урона), то в зависимости от свойств дебафа:
                              1) дебаф не наносит урон. Или нанесет через 1-6 месяцев и более. Обычно игнорируется из-за свойств человеческой памяти и психологии.
                              2) дебаф наносит урон сразу и немного. Также может быть проигнорирован, если урон терпимый
                              3) дебаф наносит случайный урон несколько раз в случайное время. По бихевиоризму — самый идеальный вариант, но обычно не реализуется из-за сложности.

                              Но в школе ни дебафы, ни бафы (положительные бонусы) не наносятся. Вариант применения бафа — еда в столовой, билеты в кино и т.д.
                              Максимальный дебаф — двойка. Максимальный баф — пятерка. И они абсолютно ничего не значат и в школе, и в реальном мире, т.к. не делают человека успешным или неудачником. Полно историй, как отличники становились неудачниками и гораздо больше, как двоечники-троечники становились успешными людьми.


                              1. khim
                                10.11.2018 19:11
                                #19349192

                                Вы опять не поняли, что я имею в виду под «отсутствием двоек».

                                Двойка — это не наказание. Двойка — это констатация факта: материал не усвоен, рассказывать что-то дальше — бессмысленно.

                                Ну вот посмотрите куда-нибудь, где диплома нет, а дают реальные знания. Скажем курсы иностранного языка. Там есть уровни и если вы не пройдёте тест — то вас не допустят в группу рассчитанную на соотвествующий уровень. Это не наказание и не поощрение — это просто способ учить только людей, которые обладают, примерно, одинаковым уровнем знаний.

                                Вот этот механизм в школе и в огромном количестве ВУЗов выключен нафиг.


                1. Oxoron Автор
                  09.11.2018 02:07
                  #19342640
                  +2

                  Ок, я поверил вам, Фихтенгольц самый простой. В том числе, благодаря примерам и приложениям. И 2000 страниц вы не считаете «водой», не так ли?

                  Я уверен, что можно добавить примеров и «мотиваций» еще на 100 страниц. Немного перемешать существующие абзацы. И тогда моментов, когда что-то непонятно, станет в два раза меньше. Как итог, скорость чтения «средним» студентом вырастет в полтора раза.

                  Работы — на несколько человеко-лет, плюс еще 5 лет экспериментов. Признаюсь, лично я не смогу выполнить эту работу в ближайшее десятилетие, но такой «апдейт» Фихтенгольца вполне возможен силами «среднего» университета (один математик, два методиста, пара аспирантов, плюс преподаватели для экспериментов). Надеюсь, вы поверите мне на слово.


                  1. akhalat
                    10.11.2018 04:40
                    #19347464

                    я написал, что фихтенгольц самый простой, наверное, потому что я сравнивал с другими учебниками, но я вас ни к чему не принуждаю. вы можете открыть любой другой, например, Зорича, Никольского, Кудрявцева, или курсы НМУ (упоминание которого весьма забавно в вашей статье, по соседству с жалобами на «сложноту» понятия предела) и сравнить наглядно. вы же предлагаете «поверить вам на слово» исходя из умозрительного эксперимента

                    теперь, вы пишите про добавление примеров и мотиваций на «100 страниц». это заниженная оценка. одних параграфов у фихтенгольца 762 штуки. добавление хотя бы одной страницы к каждому, добавит минимум 762 страницы. но ведь там бывает в одном параграфе вводится и по несколько определений

                    но такой «апдейт» Фихтенгольца вполне возможен силами «среднего» университета

                    ну во-первых, «апдейтить» таким образом Фихтенгольца вам, к счастью, не дадут, просто из-за авторских прав. проводить подобные эксперименты с лекционным курсом, основываясь на «апдейте», просто бессмысленно, по той простой причине, что целиком Фихтенгольца на лекциях не дают никогда — он просто слишком объемный — энциклопедичный, как сказано в предисловии. стандартный трехсеместровый курс анализа покрывает в лучшем случае всего лишь 30, а то и только 20 процентов всего материала. Фихтенгольц — как вам справедливо и неоднократно отмечали здесь в комментариях, всего лишь часть учебного процесса, в который входят и лекции, и семинары, и возможность непосредственного общения с преподавателями

                    а теперь представьте, сколько удастся изложить, если ещё и тратить время на «мотивирование» каждого термина. фактически, вы требуете, чтобы вам читали не анализ, а историю математики — какие задачи привели к пределу, какие к производной, к дифференциалам и т.д. и самое забавное, что в начале своего развития анализ как раз не имел точных формулировок, все понятия формулировались очень туммано и пространно, зато «простым народным языком». читать тексты и какие-то доказательства того времени — затруднительно, из-за обилия воды и непонятных рассуждений ни о чём, т.к. без отсутсвия строгих формулировок каждый был волен обращаться с пределами как ему хотелось. естественно, что куча полученных результатов тех времен оказывалась либо ошибочной, либо имела ограниченную область применимости


                    1. Oxoron Автор
                      10.11.2018 10:20
                      #19347792
                      +1

                      я написал, что фихтенгольц самый простой, наверное, потому что
                      Друг, я не спорю, что он простой. Я лишь утверждаю, что его можно сделать проще.

                      НМУ (упоминание которого весьма забавно в вашей статье, по соседству с жалобами на «сложноту» понятия предела)
                      Сложность материала, и сложность подачи материала — это разные вещи. Можно сложение 2+3 запутать коммутативностью (см Арнольда). В НМУ (в том числе судя по комментариям) умели хорошо подавать сложный материал.

                      целиком Фихтенгольца на лекциях не дают никогда
                      Без проблем. Можно поработать над теми частями, которые дают чаще всего.

                      Фихтенгольц — как вам справедливо и неоднократно отмечали здесь в комментариях, всего лишь часть учебного процесса, в который входят и лекции, и семинары, и возможность непосредственного общения с преподавателями
                      Как отмечали здесь же в комментариях, далеко не всегда можно положиться на преподавателей.

                      одних параграфов у фихтенгольца 762 штуки. добавление хотя бы одной страницы к каждому, добавит минимум 762 страницы.
                      О, понял вас. Мы по разному трактуем понятие «мотивация». Не нужно писать длинных мотивирующих постов. Часто можно просто перестроить уже имеющийся материал, с добавлением буквально пары приложений. Пример.


                      1. akhalat
                        10.11.2018 13:08
                        #19348158

                        В НМУ (в том числе судя по комментариям) умели хорошо подавать сложный материал

                        А можно пример такого комментария? Пока что, выходит совсем наоборот и НМУ это лучший пример принципа «учить плавать — скинув в воду с обрыва». Оттуда выпускается максимум 2-3 человека со всего набора на первый курс, при том что поступают туда уже сверхмотивированные люди с отличной школьной подготовкой (которые материал Фихетнгольца или его эквивалент освоили уже в школе, наряду с введением в несколько других разделов математики на уровне как минимум одгого семестра обычного ун-та). Это просто потому, что математика развита уже настолько, что материал уже некуда впихнуть. И именно поэтому сейчас новые доказательства каких-нибудь знаменитых теорем понимает лишь десяток человек во всем мире, и они годами разбирают и выверяют доказательство, параллельно делая его доступным для других математиков.

                        Я лишь утверждаю, что его можно сделать проще.

                        Я не спорю, что можно проще, но не путём добавления «мотиваций». Ну и про сами мотивации вам внизу написали несколько отличных комментариев, не вижу смысла повторяться. Добавлю лишь, что примеры в Фихтенгольце идут после определений, т.к. они их демонстрируют — невозможно демонстрировать примером определение, которого ещё нет.

                        Пример.

                        В вашем примере используется слово «сходится» которое не имеет смысла, пока оно не сформулировано чётким определением. и эти же самые примеры идут в оригинальной книге, сразу после самого определения предела, а не где-то там в конце параграфа
                        Как отмечали здесь же в комментариях, далеко не всегда можно положиться на преподавателей.

                        А вот здесь мы опять возвращаемся к уже сформулированному многими другими людьми замечанию, что ваша статья касается проблем преподавания и проблем высшего образования, чем вопросам непосредственно математики.


                      1. Druu
                        10.11.2018 13:10
                        #19348166

                        Часто можно просто перестроить уже имеющийся материал, с добавлением буквально пары приложений. Пример.

                        Так ваш пример не работает. Ваша "перестройка" ничем не лучше оригинала абсолютно.


              1. 0xd34df00d
                09.11.2018 04:11
                #19342868
                -1

                морковка

                Вы там чего-то говорили про интегралы в самом посте. А зачем эти интегралы нужны? Их даже на хлеб не намажешь, в конце концов.


                А что до методологии — ну, меня тоже в своё время очень бесила линейная алгебра, даваемая в вузе. Правда, потом я понял, что это был скорее матричный анализ, и поэтому многие вещи вроде правил перемножения матриц просто постулировались, хотя их можно вывести из нижележащей алгебраической сути линейных отображений и их композиции. И вот собственно это постулирование убивало всякое понимание.


                А потом, уже выпустившись из вуза, в поисках того, чем занять вечера, я проботал Шелдона Акслера и полюбил линал. Наверное, мозги у меня алгебраичные.


                1. SergeyMax
                  09.11.2018 13:46
                  #19344474
                  -2

                  А зачем эти интегралы нужны?
                  Интеграл — это просто перемножение двух величин, например умножение скорости на время для нахождения пройденного расстояния. Только теперь скорость может меняться.


                  1. 0xd34df00d
                    09.11.2018 17:37
                    #19345732

                    Спасибо, теперь понятно!


                    А если серьёзно, я просто немножко удивился, что автору было непонятно, зачем все эти пределы нужны, ведь интегральные суммы снизу и сверху вводятся после пределов, и без пределов их не вычислишь. И звучит всё это так, как будто полезность пределов автору неочевидна, а интегралов — очевидна, что меня несколько удивило.


                    Не, я не спорю, у меня у самого очень часто бывают вопросы «а зачем мы формулируем это определение или понятие именно так, а не иначе», но это скорее вопрос внутренней логической консистентности теории, а не её дальнейших применений.


                    1. Oxoron Автор
                      09.11.2018 17:55
                      #19345836

                      Видимо, я не совсем четко сформулировал. Сейчас я знаю, зачем нужны интегралы. Знаю, что они выводятся через верхние\нижние суммы, и пониманию назначение пределов.

                      Первокурсники не знают про интегралы, верхние и нижние суммы и прочие ништяки. Соответственно, само понятие предела им не особо и нужно. Необходимость этого понятия желательно обосновать, хоть как-то.


                      1. Druu
                        09.11.2018 21:24
                        #19346594

                        Первокурсники не знают про интегралы, верхние и нижние суммы и прочие ништяки. Соответственно, само понятие предела им не особо и нужно.

                        Так извините, а что вы предлагаете? Дать сперва какое-то определение через пределы, когда люди еще совсем не знают, что такое пределы, и сказать: "вот вам нужны пределы чтобы понять это определение"? Так это определение для них будет полный hurrdurr.


                        1. Oxoron Автор
                          09.11.2018 22:31
                          #19346844

                          Так извините, а что вы предлагаете?
                          Конкретно Фихтенгольц приводит примеры иррационального числа, и периметр вписанного правильного многоугольника. Соответственно, можно заявить: у некоторых последовательностей значения x_n «приближаются» к некоторому числу с ростом n.
                          1, 1.4, 1.41,… приближается («сходится») к корню их двух (этот пример у Фихта есть). Последовательности периметров правильных вписанных\описанных многоугольников (тут должны быть формула и рисунок) «сходятся» к длине окружности, приближая число Pi. Последовательность 1
                          1 -1/2
                          1 -1/2 + 1/3
                          1 -1/2 + 1/3 -1/4 сходится к…
                          Сходящиеся последовательности являются необходимой базой для дальнейших тем (эти темы могут быть указаны в оглавлении) и обладают собственными любопытными свойствами.

                          Далее вводим предел, даем примеры и контрпримеры типа (-1)^n, поясняем определение...

                          Собственно, я добавил буквально пару предложений к материалам Фихтенгольца. При этом минимальные изменения в порядке абзацев дают более плавный ввод терминов, простейшие примеры перекинуты ближе к определению, не заставляя читателя переворачивать страницы туда-обратно. На лекции можно мельком упомянуть «условно-сходящийся ряд», при изучении рядов студенты его «вспомнят» как нечто смутно знакомое.


                          1. Druu
                            09.11.2018 22:36
                            #19346866

                            Конкретно Фихтенгольц приводит примеры иррационального числа, и периметр вписанного правильного многоугольника.

                            Это все совершенно примитивные вещи, которые возможны исключительно на уровне введения в дисциплину. Дальше не получится. Не будет у вас просто таких вот житейских "приближается", которые достаточно близко описывают происходящее.


                            Ну и да, то что вы описали особо никакого профита не дает, вся та же самая информация содержится просто в самих словах: "предел", "стремится", "сходится" — и так понятно что что-то там к чему-то там как-то приближается, без отдельных пояснений. Проблема исключительно в том, чтобы набить руку на самом формализме — так, чтобы интуитивно думать на языке е-д, в определенных терминах, определенным способом.


                    1. ganqqwerty
                      09.11.2018 18:06
                      #19345898

                      с интегралом вроде ж оно попроще? Вот есть у тебя длина, есть площадь, есть объем — это же все очень похожие штуки в нашем чудесном евклидовом пространстве точек. Если студент понимает, что кроме него бывают другие пространства и они тоже очень полезны — ему можно объяснить, что в них понятие объема/площади тоже может пригодиться.


                      1. Ndochp
                        09.11.2018 18:59
                        #19346110

                        Угу. Площадь. Почему тогда интеграл от 0 до +бесконечности от 1/х не считается в школьных рамках, при том площадь очевидно (из симметрии графика) равна 1+(интеграл от 1 до бесконечности)*2 ( а вот выражение в скобках уже считается легко)


                        1. MikailBag
                          09.11.2018 21:30
                          #19346620
                          +3

                          Он же расходится, разве нет?


                        1. longclaps
                          09.11.2018 22:13
                          #19346804

                          Ваше утверждение фактически неверно, ввиду того, что сей график симметричен относительно прямой Y=X, а вовсе не вертикали X=1.


                      1. Druu
                        09.11.2018 21:26
                        #19346602

                        Вот есть у тебя длина, есть площадь, есть объем

                        А что такое длина, площадь и объем? Если вы попробуете это определить, то окажется что можно, с-но, многими способами неэквивалентными это сделать, единственность получается только при совпадении нескольких условий, причем для объема искомой меры не существует в принципе и надо пожертвовать либо геометрической инвариантностью, либо "всюду определенностью".


                        1. ganqqwerty
                          09.11.2018 23:05
                          #19346960

                          это все так, но я не на этом делаю акцент, а на том, что площадь, длина и объем студенту точно известны, и он явно нутром догадывается, что они очень похожи — вот от этого и надо отталкиваться


                          1. khim
                            09.11.2018 23:37
                            #19347052

                            А вот в том-то и дело, что они не «очень похожи». Или вы про сапог Шварца ничего не слышали?


                            1. ganqqwerty
                              10.11.2018 01:01
                              #19347250

                              ваши предложения?


                              1. khim
                                10.11.2018 02:06
                                #19347332

                                Перед тем, как что-то предлагать нужно вначале понять чего мы хотим получить. Если специалистов — то нужно прежде всего дать преподавателям возможность отсеивать тех, кто ни фига не знает и не умеет. Что создаст главное: мотивацию. Желание учиться.

                                А дальше — уже можно думать на тему: как сделать, чтобы человек, который хочет учиться смог бы более просто разобраться с пределами и интегралами.


                                1. akryukov
                                  10.11.2018 06:56
                                  #19347570
                                  +1

                                  Почему вы думаете, что отчисление неуспевающих будет кого-то мотивировать?
                                  По моему опыту, желание учиться появляется тогда, когда человек понимает зачем применять изучаемый материал и у него получается его осваивать.


                                  1. Druu
                                    10.11.2018 09:24
                                    #19347698
                                    +1

                                    Почему вы думаете, что отчисление неуспевающих будет кого-то мотивировать?

                                    Никого мотивировать и не надо не надо, надо просто отчислить немотивированных и работать с оставшимися. Не хочет человек учится — пусть не учится. Почему его кто-то заставлять должен?
                                    Сперва его в школе мотивируют, потом в институте мотивируют, потом на работе мотивируют: "ну давай, ну поработай немного".
                                    Прекратите этот инфантилизм уже. Дайте людям возможность быть взрослыми и нести ответственность.


                                    1. zartarn
                                      10.11.2018 10:45
                                      #19347826

                                      У нас бы на матфаке тогда осталось бы со всемго потока человека 3-4, староста, профорг и пара людей которые учить не хотят но им это дается. После чего возникли бы вопросы к факультету, уменьшили бы финансирование и т.д.


                                      1. Druu
                                        10.11.2018 13:12
                                        #19348178

                                        У нас бы на матфаке тогда осталось бы со всемго потока человека 3-4, староста, профорг и пара людей которые учить не хотят но им это дается.

                                        И в чем тут проблема?


                                        После чего возникли бы вопросы к факультету, уменьшили бы финансирование и т.д.

                                        Это отдельный вопрос, который к теме обсуждения уже не относится.


                                        1. zartarn
                                          10.11.2018 15:35
                                          #19348596

                                          И в чем тут проблема?

                                          Проблемы нет. Только скорее вопросы к преподу неже ли к ученикам.


                    1. Druu
                      09.11.2018 21:23
                      #19346588

                      зачем все эти пределы нужны, ведь интегральные суммы снизу и сверху вводятся после пределов

                      Вообще интегралы это уже следующий семестр. Непосредственно после теории пределов идут производные, которые без пределов как-то тоже не особо.


                1. kagamin
                  09.11.2018 16:15
                  #19345274
                  +1

                  Ну, это вот кстати вопрос подачи материала. В НГУ, к примеру, было принято сначала рассказать о линейных операторах, потом ввести для них матричное представление, и оттуда же вытащить умножение матриц.
                  В результате всё довольно сильно зависит от преподавателей. и пока преподавание (на всех уровнях) не станет профессией востребованной, хорошие преподаватели (а следовательно и хорошие учебники) так и будут скорее случайностью, чем закономерностью.


                  1. 0xd34df00d
                    09.11.2018 17:39
                    #19345742
                    -1

                    Ну, у нас был широко известный в узких кругах Беклемишев. Ещё были лекции другого чувака, которые были более алгебраическими, но так как Бек — физтеховский бренд, разговоров о том, чтобы ходить на те лекции и переводиться к семинаристам, идущим по тому курсу, не ходило, а я был слишком глупым и малознающим первокурсником, чтобы делать выводы самостоятельно.


            1. 3aicheg
              09.11.2018 03:51
              #19342840
              +7

              в то, что автор неспроста вставил в книгу какие-то определения и понятия с пониманием своего дела, и их важность откроется по ходу дальнейшего изучения — вы верить отказываетесь упорно, вам нужны «подтверждения» здесь и сразу, причём непременно сразу после каждого вновь вводимого определения. эдакая «морковка»


              Да не так, не в «вере» дело — просто вот читаешь текст, настолько перегруженный новыми для тебя и глубоко абстрактными понятиями — и ты его не то что не понимаешь, ты даже не понимаешь, понимаешь ты его или не понимаешь. Особенно заметно, когда читаешь с целью немедленной практической реализации: прочитал раз — не понял. Перечитал — не понял. Медленно, вдумчиво прожевал каждый параграф, пропустил через себя, актуализировал и абсорбировал материал — во, вроде, понял. Начинаешь программу писать, сразу становится ясно, что «понял» ты какой-то бред, не имеющий отношения к реальности. И это ещё хорошо, что ты хотя бы понял, что не понял — а если материал не предполагает незамедлительной практической реализации, так даже этого не поймёшь, уйдёшь дальше в жизнь с иллюзией понимания.


            1. hardmodebitch
              09.11.2018 09:44
              #19343330
              +8

              Человеческий мозг не запоминает вещи просто потому что «надо и всё тут».
              Он запоминает вещи потому, что ему это надо зачем-то.
              И чтобы человек какую-то вещь своим мозгом понял и запомнил, ему нужно сначала понять, а как эта вещь ему поможет лучше выживать.

              И если я хочу моделировать физические процессы на компьютере, а мне на первом курсе суют гору матана и говорят «нада!», не объясняя, как мне это поможет научиться моделировать эти самые процессы, я ничего не запомню.
              Я сдам сессию и забуду всё к чертям.
              А через несколько лет, изучив кучу других дисциплин, я пойму, зачем мне может понадобиться матан, но будет уже поздно.

              Такие дела.


              1. ankh1989
                09.11.2018 12:16
                #19344012

                Иногда мозг запоминает совершенно бесполезные вещи. Например нафига я до сих пор помню формулу этил-с2-диизопропиламиноэтилметилфосфонотиолата? Видел один раз лет 15 назад. Запомнилось железно.


              1. klvov
                09.11.2018 13:27
                #19344374
                +5

                Воистину, по современным представлениям психологической науки, все именно так. Почему это до академической среды так медленно доходит, не знаю, наверное из-за инертности системы.

                Вспомнилось, как в какой-то книге Фейнман описывал, как он приехал в Бразилию, что ли, и увидел, что студенты там совершенно не понимают смысла формул, которые они заучили и кое-как применяют в стандартных кейсах (которые они тоже заучили), но чуть шаг в сторону, и они впадают в ступор. Это когда его попросили высказать мнение, что не так в системе образования в этой стране. Он потом отвечал на это, что главное не формулы заучивать, а создавать понимание, что эти формулы означают (а также как их получить и почему они именно такие).

                Оставлю вот еще ссылку на сайт, который понравился: BetterExplained — Math lessons that click. Например, там есть статья про формулу Эйлера


                1. Druu
                  09.11.2018 15:12
                  #19344952

                  Например, там есть статья про формулу Эйлера

                  Это не формула Эйлера, это ее частный случай.


            1. hardmodebitch
              09.11.2018 10:36
              #19343462

              Забавно, что в соседнем посте про комплексные числа вы же сами пишете:

              гораздо полезнее было бы, если бы автор написал какую-то задачу из своего практического опыта, где возникла потребность прибегнуть к этим числам, или хотя бы рассмотрел какой-то алгоритм (уверен, в кормене можно откопать) на их основе, и уже по ходу дела объяснил что они и зачём


              1. mayorovp
                09.11.2018 10:53
                #19343546

                Так пост же не является главой из учебника. Формат разный...


          1. sergeperovsky
            10.11.2018 10:08
            #19347760

            «выделены курсивом понятия величина, переменная, постоянная, множество, направленная переменная, предел, последовательность».
            Хоть для школьников, хоть для студентов начинаю объяснения с одной идеи: математика это сказка. Любая математическая теория неявно начинается со слов: «Представим себе мир, в котором существуют такие-то объекты с такими-то свойствами и действуют такие-то законы. И посмотрим, что в таком мире возможно, а что нет». Когда-то математики заботились о том, чтобы придумываемый мир напоминал реальный. Потом поняли, что это абсолютно не важно. Удастся ли поставить в соответствие математической теории какие-то явления реального мира — дело физиков и прочих естественников.
            В школьной программе этот подход не приветствуется, считается, что на примерах из реального мира разбирать математику проще. В вузе для физиков или инженеров тоже полезны примеры. И их стараются приводить. Но при подготовке профессиональных математиков это уже не обязательно. А может быть и вредно.


            1. Dr_Faksov
              10.11.2018 18:08
              #19349022

              Математикам НЕЛЬЗЯ давать ПРИДУМЫВАТЬ примеры из жизни. Задачу про бассейн и трубы через которые втекает и вытекает помните? Для начальных класов вроде…
              А ничего что скорость вытекания зависит от высоты столба жидкости? Да еще там зависимость степенная, сколько помню. Там интеграл брать самый раз, я так думаю.


              1. Maxim_Andreev
                10.11.2018 18:45
                #19349146

                Вы очень трудную тему затронули) Такая ошибка была даже у авторов задачи для международной (СНГшной) олимпиады по гидравлике. Там предлагалось посчитать (с интегралом) за сколько жидкость выливается из одного и другого отверстия вращающегося сосуда по отдельности, а потом определить время опорожнения из двух отверстий по школьной формуле для общей работы (не учитывая, что там вообще-то будет взаимовлияние).


                1. akhalat
                  10.11.2018 19:03
                  #19349176

                  а что за задачка, можно ссылки?


                  1. Maxim_Andreev
                    10.11.2018 19:27
                    #19349216

                    В интернетах, к сожалению, не нашёл, а оригинал утрачен при переездах. Речь об олимпиаде по гидравлике в Одессе при Институте холода в 2008-м году, если мне не изменяет память.
                    Суть задачи заключается в том, что есть вращающийся сосуд, в дне которого на разном расстоянии от центра просверлены отверстия, через которые выливается жидкость. Нужно определить время максимального опорожнения для каждого из отверстий и для двух отверстий вместе. Ну и по-моему, сколько жидкости останется в каждом из этих случаев.
                    В случае отдельных отверстий всё просто: строится поверхность жидкости (парабола) и через интеграл считается время, когда парабола коснётся отверстия. А для двух отверстий интеграл аналитически не берётся. Авторами задачи в «правильном» решении предлагалось посчитать время по общей работе. Уже после олимпиады наша кафедра (гидравлики, МГТУ им. Баумана) повозмущалась, но, понятное дело, ни к чему это не привело. Через пару лет вообще разругались с организаторами, и вроде до сих пор МГТУ им. Баумана в этих олимпиадах не участвует)


                    1. akhalat
                      10.11.2018 19:49
                      #19349258

                      хех, помню само мгту проводило олимпиаду по физике (как раз вроде в 2008) где в условиях механической задачи предполагалось не учитывать трение, хотя это делало условие физически некорректным (без трения указанный процесс просто не мог осуществиться). при этом, решение с учетом трения было элементарным, пусть и немного хитрым — но его организаторы не засчитывали, настаивая на своем неправильном (притом ответы совпадали)
                      так что такое сплошь и рядом


                      1. Maxim_Andreev
                        10.11.2018 20:31
                        #19349348

                        Ну я о том и говорю, что когда сплошь и рядом встречаешь такие косяки авторов задач на университетских всероссийских олимпиадах, школьные задачки с трубами и бассейном уже и не кажутся такими уж бредовыми)
                        В конце концов, все задачки с «правильным ответом» призваны продемонстрировать владение конкретным методом и умением действовать в определённой ситуации по определённому лекалу. Это тоже в целом неплохой навык, а уж тренировать креативность лучше в рамках какой-то проектной работы.


              1. sergeperovsky
                11.11.2018 03:12
                #19350232

                Математики всегда будут рассматривать сферического коня в вакууме. Особенно, если речь идет о примерах для школьников.
                Велосипедист из пункта А в пункт Б не будет ехать с постоянной скоростью. Землекоп не выкопает за 8-й час работы столько же, сколько за первый.
                Все примеры из задачника по математике имеют к жизни косвенное отношение.
                Это просто способ представить условия задачи наглядно.
                Даже яблоки подсчитать можно только условно — они же разные.
                -У тебя было шесть яблок, половину отдал другу, сколько осталось?
                -Пять с половиной.
                Первая фраза из парижской лекции известного математика «математические основы конструирования одежды»: для простоты представим, что человеческое тело имеет форму шара.


        1. 0xd34df00d
          09.11.2018 04:06
          #19342858
          -1

          весь «матан» — это учение о бесконечно малых, строго и корректно это понятие можно определить лишь с помощью предела

          Я тоже когда-то так думал, а потом… Ну, в общем, строго и корректно это можно определить ещё и при помощи логики первого порядка и теории моделей (см. неклассический анализ). Меня прям вштырило с этого вот.


          Правда, я бы сказал, что матлогика и теория моделей чуть более требовательны к математической дисциплине, абстрактному мышлению и умению не задавать вопросы «а нахрена это надо в глобальном плане» (или просто любви к предмету, чтобы оно было самоцелью?), чем какие-то там пределы.


        1. WinPooh73
          09.11.2018 13:14
          #19344318
          +7

          Популярный в СССР учебник теорвера Елены Вентцель тоже переполнен практическими примерами. В основном они затрагивают теорию бомбометания, баллистические задачи, системы распознавания "свой-чужой" и прочие, не менее актуальные прикладные вопросы.


          1. Zenitchik
            09.11.2018 14:14
            #19344614
            +2

            Это же замечательно!


        1. roman_kashitsyn
          09.11.2018 13:31
          #19344388
          +3

          вообще, фихтенгольц — это простейшая книга по матану, где всё разжёвывается до мелочей и читателя просто закидывают разнообразными примерами, настолько приближенными к практике, насколько это возможно

          Подтверждаю. Я на втором курсе перечитывал этот учебник (начались диффуры, хотелось ещё раз подтянуть матчасть). Он читается как художественная литература. У меня до сих пор дома тома стоят, так и тянет ещё раз почитать.


          Но часть критики в статье я всё же считаю верной. Например, зачастую в учебниках не хватает бэкграунда, процесса становления. Математику в учебниках описывают от общего к частному, а ведь развивается она в обратном направлении: есть конкретные задачи, люди придумывают методы их решения, а потом потихоньку обобщают. Если показываешь сразу готовое комплекстное решение, понять его гораздо сложнее, потому что непонятно, как ко всему этому пришли.


          Особенно полезно самому выводить формулы, после этого их уже не нужно помнить, можно помнить только ключевую идею. Более того, вывод формул может приносить огромное удовольствие, ведь каждый раз это как маленькое открытие.


          1. Druu
            09.11.2018 15:14
            #19344958

            Он читается как художественная литература.

            Кстати, да. Фихтенгольца можно читать просто как сказку на ночь, и сама манера письма у него соответствующая, с прикольными атмосферными оборотами. По-этому Фихтенгольц обычно либо очень нравится, либо его ненавидят :)


        1. ganqqwerty
          09.11.2018 17:22
          #19345656
          +1

          Давайте глубже копнем. «Это учение о бесконечно малых». А зачем нам бесконечно малые, почему они полезны или интересны?


          1. Druu
            09.11.2018 21:28
            #19346610

            А зачем нам бесконечно малые, почему они полезны или интересны?

            Чтобы это нормально объяснить придется заходить еще с апорий Зенона. И самое печальное, что даже если все это студенту объяснить — пониманию это никак способствовать не будет. Наоборот, он скажет — нахрена вы еще какой-то лишней хренью мне мозг грузите.


            1. akryukov
              09.11.2018 21:54
              #19346710

              Нельзя ли начать с аналогии про молекулы и атомы? Ну вот есть у нас какие-то крайне малые сущности, которые мы не видим, но которые формируют окружающий мир и влияют на свойства вещей.


              1. Druu
                09.11.2018 22:08
                #19346776
                +1

                Нельзя ли начать с аналогии про молекулы и атомы?

                Вообще не вижу, каким образом можно молекулы и атомы притянуть к бесконечно малым.


              1. khim
                09.11.2018 23:43
                #19347072

                Ну если вы хотите человека полностью и окончательно запутать — тогда вперёд.

                Ибо если использовать классическую физику и начать с молекул и атомов — то вы получите мир, который и близко не похож на реальный (именно поэтому его так сложно моделировать на компьютерах… они ж у нас классические — нолики и единички).

                Чтобы физику и молекулы/атомы сдружить вам нужна квантовая механика и Уравнение Шрёдингера. Как вы это вообще собрались рассказывать человеку, которые ни о пределех, ни о производной понятия не имеет?


                1. akryukov
                  10.11.2018 07:01
                  #19347574
                  -1

                  Почему вы думаете, что молекулы, атомы нам нужны для формулирования непротиворечивых теорий?
                  Я же предлагаю такую аналогию только для того, чтобы донести до студентов ответ "Почему нам важно обращать внимание на бесконечно малые значения?".


                  1. Druu
                    10.11.2018 09:27
                    #19347702
                    +1

                    Извините, но вот я уже знаю матан, работа с пределами и е-д формализмом мне не доставляет проблем, кроме того я могу работать с бм при помощи нестандартного анализа (альтернативный вариант).
                    И мне ваша аналогия ну совсем непонятна и ничего до меня не доносит. Искренне сомневаюсь, что она что-то в принципе до кого-то могла бы донести.


                    1. akryukov
                      10.11.2018 16:50
                      #19348794

                      Было бы странно ожидать, что аналогия, предназначенная для ничего не понимающих студентов, донесла бы вам что-то новое.
                      Что, впрочем, не исключает негодности аналогии. Мне еще не приходилось объяснять пределы.


            1. ganqqwerty
              09.11.2018 23:07
              #19346968

              ну, можно с зенона, а я уверен, что можно еще как-нибудь. Вот например через те же самые треугольнички из статьи — ведь чем они меньше по размеру, тем вычисление у нас точнее.


            1. saboteur_kiev
              10.11.2018 01:57
              #19347320

              Знаете, вот именно так и получается в википедии. Вместо того, чтобы подумать и пояснить на простых примерах, зачем нам вечно малые, начинают рассказывать что это очень сложно.

              Ну вот проблему бесконечно малого отрезка времени объяснить очень легко — когда тебе нужно засечь время, ты нажимаешь кнопку на секундомере, а потом нажимаешь второй раз и все.
              А если тебе нужно засечь гораздо меньший отрезок, чем ты можешь нажать — у тебя возникают проблемы. И есть промежутки, которые не успевает засечь даже процессор.

              Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона, ты его физически увидеть не можешь, как бы ты не увеличивал.

              Видите как в физике все просто.

              Почему же в математике начинают эту лишнюю хрень?


              1. khim
                10.11.2018 02:23
                #19347360

                Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона
                У фотона нет размера. Возможно вы имеете в виду длину волны?

                ты его физически увидеть не можешь, как бы ты не увеличивал.
                И наоборот, нельзя «нарисовать» картинку, с характерным размером меньше, чем длина волны, да? А ничего, что вы вот этим вот строки набираете на «невозможном» компьютере, в котором используется «невозможный» процессор? Напомню, что в современной литограции используется 193нм лазер, а техпроцессы с такими огромными транзисторами — это «прошлый век». Буквально.

                Почему же в математике начинают эту лишнюю хрень?
                Потому что для физика нормально сказать «если A и B, то C, мамой клянусь»… а потом, оп-па, взять — и забрать свои слова обратно. Как в ваших рассказах про «размеры фотона» и «предменты».

                А в математике — нет. Если теорема верна и в доказательстве нет ошибок — то она таки верна.


                1. saboteur_kiev
                  10.11.2018 15:02
                  #19348488

                  У фотона нет размера. Возможно вы имеете в виду длину волны?

                  Вот именно в этом заключается проблема.

                  Мы сейчас не обсуждаем что такое фотон, я пытался привести пример простым языком, почему нельзя сделать оптический микроскоп, который увидит бесконечно малое.
                  Любой школьник, примерно слышавший о фотоне, поймет.

                  А вы тут же хотите все усложнить, довести до формального, то есть сделать собственно то о чем речь в статье.


              1. akhalat
                10.11.2018 04:56
                #19347478

                > Почему же в математике начинают эту лишнюю хрень?

                вы, наверное, просто не знаете как в физике определяют фотон — не для популярных обзоров, а именно для того чтобы реально с ним работать и выдавать какие-то результаты для применения на практике или в экспериментах. эта «хрень» будет в сто раз сложнее курса матана


              1. Druu
                10.11.2018 09:28
                #19347706

                Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона, ты его физически увидеть не можешь, как бы ты не увеличивал.

                Нет, проблема не в этом.


    1. Centimo
      09.11.2018 14:12
      #19344606

      на самом деле, единственная проблема в том, что «матан» ставят в учебные планы тех специальностей, которым он на таком уровне не нужен. это действительно проблема наших реалий, на западе это решается наличием курсов на выбор и совсем упрощенными курсами типа calculus где всё объясняется на пальцах


      Позвольте не согласиться с «ненужностью» матана. Считаю, что в текущих реалиях первые пару курсов технического универа (пусть и обрезанные) необходимы всем. Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять, владел каким-то базовым пониманием теории вероятностей и статистики. С текущей модой на демократию каждый человек должен иметь возможность критически воспринимать информацию, иначе мы получим то, что имеем.


      1. Druu
        09.11.2018 15:16
        #19344976
        -1

        Чтобы даже самый гуманитарный

        Нет, гуманитарию не надо ни интегралы, ни матрицы, ни индукции. Математику у гуманитариев надо выкинуть, а вместо нее добавить историю математики, с кратким обзором направлений, парадоксами "на пальцах", и прочими интересными вещами. Ну это как на уроках литературы вас не учат писать стихи, вам рассказывают про тех, кто их писал и приводят примеры стихов. Аналогичная ситуация, не надо учить гуманитариев заниматься математикой, надо просто рассказывать — про математику и людей, которые ей занимаются.


        1. Centimo
          09.11.2018 16:17
          #19345288
          +3

          с кратким обзором направлений, парадоксами «на пальцах», и прочими интересными вещами

          Потом это «на пальцах» легко превращается в непонимание, а то и в лженауку. Поэтому-то и воду заряжали (и заряжают) от телевизора — людей научили, что есть какие-то лучи, а что это и на каких принципах оно работает не объяснили.
          Ну это как на уроках литературы вас не учат писать стихи

          Я думаю, если бы можно было научить писать стихи, то этому бы учили. Это то же самое, что обучить рисовать картины. Можно обучиться технике, но нельзя (на данный момент) научиться быть хорошим художником.
          Я и предлагаю учить не решать проблемы тысячелетия (рисовать картины), а учить базовым вещам (технике рисования).


          1. Zenitchik
            09.11.2018 18:22
            #19345970

            Можно обучиться технике, но нельзя (на данный момент) научиться быть хорошим художником.

            Если бы учили хотя бы технике — глядишь и хороших художников было бы побольше. Из-за того, что не учат — кто-то просто не попробовал…


          1. Druu
            09.11.2018 21:30
            #19346624

            Потом это «на пальцах» легко превращается в непонимание, а то и в лженауку.

            Конечно же не превращается, есть вещи, которые можно достаточно строго изложить, не предполагая у слушателя математической подготовки выше самой базовой (основы алгебры, арифметики, геометрии). Штука в том что это именно отдельные примеры — что и нужно гуманитариям.


            Я и предлагаю учить не решать проблемы тысячелетия (рисовать картины), а учить базовым вещам (технике рисования).

            Технике надо учить того, кто потом ей будет пользоваться. Учительница английского будущая — не будет. Ей нужна не техника, а культура.
            Зачем учить меня каким-то хитрым мазкам или способам смешивания краски, если я рисовать картины не хочу и вообще это дело ненавижу? А вот рассказать об истории живописи, дать обзор существующих направлений, рассмотреть конкретные картины и дать их анализ — это вполне ок.


            Есть разница между писателем и читателем, понимаете? Учить писать надо того, кто будет писать.


            1. Centimo
              09.11.2018 21:50
              #19346700

              Только разница между рисованием и математикой в том, что технику мазков может нигде больше и не получится использоваться, а вот на основах математики построен мир. Может учительнице английского никогда и не пригодится непосредственно понимание определения предела, но уж точно лишним не может и строгости мысли добавит.


              1. Druu
                09.11.2018 22:09
                #19346782

                Только разница между рисованием и математикой в том, что технику мазков может нигде больше и не получится использоваться, а вот на основах математики построен мир.

                Это все замечательно, но, еще раз, техника математики (и вообще чего угодно) нужна тем и только тем кто потом будет заниматься математикой (или чем угодно). Вот и все.


                Может учительнице английского никогда и не пригодится непосредственно понимание определения предела, но уж точно лишним не может и строгости мысли добавит.

                Ничего оно ей не добавит кроме головной боли.


            1. Zenitchik
              09.11.2018 22:17
              #19346818

              Учительница английского будущая — не будет.

              А может будет? Вы сперва научите.


              1. Druu
                09.11.2018 22:21
                #19346822

                А может будет? Вы сперва научите.

                А она того хочет? Вы ее спросили? Она же решила стать учительницей английского. Если бы она хотела быть математиком — она бы пошла учиться на математика, а не на учительницу английского.
                Давайте мб вас силой заставим учиться писать картины, петь, играть на балалайке, танцевать твист и играть в го?


        1. Zenitchik
          09.11.2018 16:18
          #19345296
          +1

          Нет, гуманитарию не надо ни интегралы, ни матрицы, ни индукции.

          И чем же он сможет заниматься без всего этого? Я сегодня утром задумался: придумал две профессии с высшим образованием, но без математики: переводчик и врач (и то не всякий).
          Сможете ещё придумать?
          не надо учить гуманитариев заниматься математикой

          Пока не заставишь человека попробовать заниматься математикой — не поймёшь, гуманитарий он или нет.


          1. 0xd34df00d
            09.11.2018 17:49
            #19345792

            Программировать можно, например (с точностью до математики в предметной области, веб-странички, наверное, можно и без интегралов и индукций делать). Сейлзом быть. Эйчаром. Проджекты манаджерить. Или людей.


            Можно быть юристом. Переводчиком. Архитектором — у моего знакомого была девушка, училась на архитектора, доучивалась в США, математики у неё было полгода примерно так же, как у меня на Физтехе было полгода риторики или апологетики христианства, которые я взял just for lulz как гумкурсы по выбору, а весь сопромат и утечки тепла программа на комплюктере у них там считает. Да мало ли.


            Мне было сложнее вспомнить, кто ещё бывает, кроме всяких программистов и математиков, чем отфильтровать этот список по требованию матана.


            1. Zenitchik
              09.11.2018 21:37
              #19346642

              Я специально сказал «с высшим образованием». Вот я — учился на инженера, работаю программистом. Пригождается мне высшее образование? Как бы не так! Занимаюсь ремеслом! А чтобы почувствовать себя программистом — академической математики не хватает.
              Менеджер, юрист. Согласен. Переводчика — сам назвал, это моя жена. Её сестра — архитектор, если бы ей не давали сопромат, то что бы тогда осталось?
              Ещё одна моя знакомая — инженер-конструктор изделий из кожи. У них была настоящая теплотехника, я даже удивился (сам с ужасом вспоминаю тройные интегралы от гауссинады).


            1. khim
              09.11.2018 23:45
              #19347080

              а весь сопромат и утечки тепла программа на комплюктере у них там считает
              А потом мосты рушатся, так как «архитекторы с дипломом» не понимают, когда выходят за рамки применимости заложенных в эти программы моделей.


              1. akryukov
                10.11.2018 07:04
                #19347576

                Есть конкретные примеры мостов, которые разрушились от того, что архитекторы с дипломом вышли за рамки применимости моделей?


                1. khim
                  10.11.2018 18:23
                  #19349078

                  Разумеется. Вот мостик. Вот домик. Вот школа.

                  Это то, что навскидку нашлось. А так — это, увы, типичное явление.


          1. Druu
            09.11.2018 21:33
            #19346632

            И чем же он сможет заниматься без всего этого?

            ДА практически чем угодно, в 99% профессий ни интегралы ни матрицы вам не понадобятся.


            1. Zenitchik
              09.11.2018 21:48
              #19346684
              +2

              в 99% профессий ни интегралы ни матрицы вам не понадобятся.

              И высшее образование тоже. Ну, разве что «для галочки».


              1. Druu
                09.11.2018 22:11
                #19346796

                И высшее образование тоже.

                окей
                в 99% профессий где нужно высшее образование игтегралы тоже не понадобятся. С-но, кому понадобятся интегралы:


                1. математики, физики, прочие ученые-технари и их обслуживающие
                2. инженеры
                3. конец списка


                1. Zenitchik
                  09.11.2018 22:23
                  #19346828

                  математики, физики, прочие ученые-технари и их обслуживающие
                  инженеры

                  Забыли учёных-естественников, которым математика год от года всё нужнее.

                  Ну, вероятно, вы сумеете доказать, что всё это вместе — процент от числа профессий, где нужно высшее образование.
                  Потому что если считать по моим знакомым с высшим образованием — одних только инженеров процентов 20%.


                  1. Druu
                    09.11.2018 22:28
                    #19346834

                    Забыли учёных-естественников

                    Ну я сказал — ученые технари


                    Ну, вероятно, вы сумеете доказать, что всё это вместе — процент от числа профессий, где нужно высшее образование.

                    Это фактически две профессии.


                    Потому что если считать по моим знакомым с высшим образованием — одних только инженеров процентов 20%.

                    Вы кого именно подразумеваете под инженерами? Давайте сразу оговоримся — программисты и прочие итшники это не инженеры. Инженеры — это которые строят самолеты, проектируют двигатели и атомные электростанции.


                1. IvanTamerlan
                  09.11.2018 23:13
                  #19346984

                  К сожалению, математику надо еще подружить с физикой.
                  Учусь на один из подвидов экономиста и тут изучают математику без физики, поэтому иногда математически верные расчеты при физическом сопоставлении с задачей превращается в непроходимый бред. А еще у нас(экономистов) математика преподается слабее и в учебниках по экономики даются входные данные, диф.ур. и сразу результат без вывода и преобразований, в стиле «поверьте на слово». Дали математикам пересчитать — их результат с результатом из учебника не сошелся.

                  Вроде экономист должен быть ближе к инженерам по подготовке, т.к. от экономиста зависит проект иной раз больше, чем от инженера. Например, инженер сообщает: — мы может сделать такую деталь в 4-х вариантах, в каждом упор на такие-то свойства.
                  И уже экономист считает альтернативные расходы, экономическую эффективность и прочие показатели, на базе которых находит сбалансированное решение. Но современные экономисты ищут не сбалансированное решение, а «правильное», которое в реальном мире может не существовать. Я молчу про привычку экономистов все переводить в деньги, что приводит к «эффективному менеджменту»: «деньги за каждую строчку кода» и стилю кода «индусский код».


      1. 0xd34df00d
        09.11.2018 17:44
        #19345768

        Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять

        Как бы вы объясняли математическую индукцию для гуманитариев?


        Рассказывали бы вы про вполне упорядоченные множества, про аксиому выбора с леммой Цорна? Или так, чё-то там на Nat фигак-фигак и доказали?


  1. kkirsanov2
    08.11.2018 22:33
    #19342014
    +15

    Статья называется «Проблемы современной записи математических текстов» но весь текст посвящен проблеме преподавания. Это сбивает с толку.

    1) Хочу защитить Фихтенгольца. Его учебник, один из выдающихся, является частью образовательного процесса в котором должны быть и лекции и семинары, и тут талант автора учебника вполне может быть испорчен безаталанностью лектора.

    2) Про «реальные проблемы». В рамках семинара или лекции с небольшим числом слушающих можно прощупывать почву и подгонять материал под аудиторию. При написании учебника для широкой аудитории это невозможно и лучше как раз оставлять стерильные формулировки, которые на местах уже адаптируют.

    Вот например лет десять назад Питер издали классную Дискретную Математику для программистов (это я как программист с преподавательским опытом оцениваю). Но для не программистов я бы рекомендовал другой учебник.

    3) «У профессоров математики хватает своих задач, чтобы писать учебники.»
    Не достаточно быть талантом в своей профессии что бы писать хорошие учебники.

    Нужно что бы талант в математике совпал с талантом в педагогике и писательстве. Это на столько редкое явление что даже слабые приближения к идеалу не сходят с полок годами.

    Но всё это меркнет с общей проблемой ВО в России — многим было бы достаточно для счастливой жизни и училища но традиция, общество и военкомат влекут всех в стены ВУЗов, где боль, страдания и скрежет зубовный.


    1. Oxoron Автор
      08.11.2018 23:00
      #19342126
      +3

      Статья называется «Проблемы современной записи математических текстов» но весь текст посвящен проблеме преподавания. Это сбивает с толку.
      Вы во многом правы. Увы, большая часть виденных мною «профессиональных» работ по понятности была хуже учебников. Плюс, школьная\университетская литература известна большинству на хабре, а «профессиональная» — процентам.

      Хочу защитить Фихтенгольца. Его учебник, один из выдающихся, является частью образовательного процесса в котором должны быть и лекции и семинары
      Фихт крут, не спорю. Но учебный процесс предполагает наличие лектора, который, скорее всего, не обладает талантом\подготовкой педагога. Плюс, в наше время хайпится самообразование, и рассчитывать на помощь лектора не приходится.
      Уверен, Фихтенгольц написал один из лучших учебников своего времени, но времена меняются.

      При написании учебника для широкой аудитории… лучше как раз оставлять стерильные формулировки, которые на местах уже адаптируют.
      Опять-таки, мы живем во времена стартапов. Одно из сопутствующих поверий: лучше удовлетворить потребности одной группы пользователей на 100%, чем потребности трех групп на 80%. Дискретная Математика Для Программистов зайдет одной группе, Дискретная Математика Для Лириков — другой. В идеале, хотелось бы иметь большой учебник, из которого относительно легко вырывались бы куски для целевых групп. Вопрос цены и усилий на несколько учебников вместо одного остается открытым, да.

      Нужно что бы талант в математике совпал с талантом в педагогике и писательстве. Это на столько редкое явление
      Полностью и абсолютно согласен. Поэтому и упомянул про командную работу. Лучше иметь отличный учебник от трех авторов, чем три посредственных от каждого.


      1. third112
        09.11.2018 02:38
        #19342724
        +2

        Уверен, Фихтенгольц написал один из лучших учебников своего времени, но времена меняются.
        Я с матаном после второго курса (давно это было) очень мало сталкивался — много больше с «линейкой», комбинаторикой, графами. Поэтому любопытно: есть сегодня современный учебник по матану, который сильно превосходит Фихтенгольца? (Дайте, пожалуйста, ссылку — полистаю из интереса).


    1. khim
      09.11.2018 17:05
      #19345584
      +4

      Нужно что бы талант в математике совпал с талантом в педагогике и писательстве.
      Совершенно необязательно. Более того — человек, которому «хорошо даётся» что-то скорее всего напишет хреновый учебник. Он напишет «очевидно» не потому, что потеряет две страницы выкладок в трамвае, а потому, что ему — действительно очевидно!

      Есть профессионалы, которые умеют ещё и объяснять (Фейнман, к примеру), но вообще — для написания хорошего учебника нужно быть скорее хорошим педагогом, чем хорошим математиком…


  1. Daddy_Cool
    08.11.2018 22:59
    #19342118
    +7

    О, да!
    С преподаванием математики — проблем куча. Вставлю пять копеек.
    1. Обычно это преподавание математики для… математиков. Физическая, экономическая, жизненная, философская подоплека остается за кадром. В результате мотивация страдает дичайшим образом. Но… чтобы всё донести нужно время и заинтересованность преподавателя и студентов. По наблюдениям — какому-то проценту умненьких студентов понятно и так, а оставшимся — бесполезно и не пригодится.
    2. Обучение решению стандартных задач стандартными методами. Т.е. увы — математика не очень-то учит думать. Разные курсы физики в этом смысле у нас лучше — там надо все же модели строить.
    3. Обратная связь — в школе есть ежедневная проверка тетрадей. В институте — нет. Реально хорошую работу со студентами — с въедливыми правками в каждом пункте студенческих поползновений наблюдал только на семинарах мехмата МГУ.
    4. Наверное могли бы помочь книги типа «Высшая математика для гиперчайников», или «Высшая математика человеческим языком» — и в принципе не так сложно это сделать — просто по тому же Фихтенгольцу пройтись и переписать в забавном виде. Хотя может оно уже и есть.
    5. Но не всё просто — те же математические определения они СТРОГИЕ — это архиважно. И после понимания смысла на пальцах, надо расшифровывать строгое определение и соотносить его с реальностью.
    6-я копейка.
    Кто не читал «Плач математика» Пола Локхарда — стоит прочитать.


    1. Oxoron Автор
      08.11.2018 23:28
      #19342194

      Согласен со всеми пятью копейками. По поводу четвертой: есть книги для чайников. В моем случае для меня одного экзамена зашли конспекты Письменного (дополняемые Фихтенгольцем). Для следующего экзамена, правда, уже не зашли.


      1. ganqqwerty
        09.11.2018 17:33
        #19345708

        Письменный реально спасал меня, выпускника школы с углубленным изучением русской литературы.


    1. 0xd34df00d
      09.11.2018 06:54
      #19343018

      Обучение решению стандартных задач стандартными методами. Т.е. увы — математика не очень-то учит думать.

      Математика разная бывает. Какие-нибудь урматы — да, именно так, просто учимся решать задачки. Что-то более абстрактно-изящное — неа, вполне себе учит, ИМХО.


    1. Mikihiso
      09.11.2018 13:07
      #19344294

      4. Наверное могли бы помочь книги типа «Высшая математика для гиперчайников», или «Высшая математика человеческим языком» — и в принципе не так сложно это сделать — просто по тому же Фихтенгольцу пройтись и переписать в забавном виде. Хотя может оно уже и есть.

      Видел матан в комиксах.


      1. dee3mon
        09.11.2018 16:02
        #19345204
        +4

        Ха, вот вам отдельные математические манги
        1. Син, Т. Занимательная статистика. Факторный анализ. Манга
        2. Митио, С. Занимательная математика. Анализ Фурье. Манга
        3. Син, Т. Занимательная статистика. Регрессионный анализ.
        4. Тахакаси, С. Занимательная статистика. Манга
        5. Хироюки Кодзима, Cин Тогами, Занимательная математика. Производные и интегралы. Манга
        6. Минору С., Занимательная математика. Дифференциальные уравнения. Манга
        7. Син Такахаси, Иноуэ Ироха, Занимательная математика. Линейная алгебра. Манга
        Кому надо по физике?
        1. Нитта, Х. Занимательная физика. Механика. Манга
        2. Томохиро, Х. Занимательная физика. Термодинамика. Манга
        3. Ёсикадзу, И. Занимательная физика. Электрические цепи. Манга
        4. Фудзитаки, К. Занимательная физика. Электричество. Манга
        5. Такэи, М. Занимательная физика. Гидродинамика. Манга
        6. Исикава, К. Занимательная физика. Квантовая механика. Манга
        7. Ямамото, М. Занимательная физика. Теория относительности. Манга
        8. Суэмасу, Х. Занимательная физика. Сопротивление материалов. Манга
        Кому чуть-чуть информатики и программирования?
        1. Мана, Т. Занимательное программирование. Базы данных. Манга
        2. Сибуя, М. Занимательная информатика. Центральный процессор. Манга
        3. Митани Масааки, Сато Синъити, Хиноки Идэро, Занимательная информатика. Криптография. Манга
        И это далеко не все…


        1. ganqqwerty
          09.11.2018 17:35
          #19345722

          я по нейронауке читал эту мангу и по биохимии. Мне показалось, что фигня — просто куски учебника вставляются в баблы над головами героев повествования.


    1. Ingref
      10.11.2018 17:43
      #19348926

      Кстати, у того же Пола Локхарта есть, собственно, та самая «Математика для гиперчайников» — ru.b-ok.org/book/2474364/ab5400

      Русского перевода пока нет, к сожалению. Но она написана настолько простым языком, что и Google Translate хватает.


  1. denisart
    08.11.2018 23:00
    #19342132

    Просто вы читаете плохие книги.

    Наверняка в высших разделах математики подход «сначала пример, потом абстракция» не сработает.


    Сработает. Редко, когда в математике что-то появляется совсем с потолка. А даже если и появляется, то попадает на всеобщее обозрение не просто так.


    1. Zenitchik
      09.11.2018 14:21
      #19344644

      Меня этот подход в любых разделах любых наук бесит неописуемо. Нахрена мне пример, если я его понять не могу? На третьем подобном «примере» отпадает желание читать дальше.


  1. firk
    08.11.2018 23:37
    #19342228
    +3

    Во-первых, название статьи совершенно не связано с её содержанием.
    Во-вторых, касательно претензий образованию.
    По-моему, в школьном курсе действительно есть места, где следовало, во-первых, дать понимание того, откуда это взялось (пример с формулой дискриминанта) а во-вторых — доходчивее объяснить зачем это нужно (конкретный пример привести затрудняюсь, но такое точно было).
    Но вот в вузовском курсе подобные претензии, по-моему, уже совершенно необоснованы. Он, с одной стороны, и так хорошо структурирован (потому как нет необходимости уместить кучу разнородных мелочей в один краткий курс), а, с другой, предназначен для уже сформировавшихся интеллектуально личностей, и тащить туда объяснения для, грубо говоря, идиотов — лишняя потеря времени и места в учебнике.
    Ну и с фразой, вами упомянутой


    Дай вопрошающему грош, если он ищет выгоды, а не математики

    полностью согласен.
    Дай вопрошающему грош, если он ищет выгоды, а не математики


    1. ganqqwerty
      09.11.2018 17:37
      #19345734
      +1

      для уже сформировавшихся интеллектуально личностей

      Вы слишком высокого мнения о нас. Говорить о каком-то формировании лично в моем случае можно было ну где-то после лет 26-ти.


  1. geisha
    08.11.2018 23:54
    #19342308
    +4

    Как отметили выше, вы описали проблемы преподавания матана, а не проблемы с записью математических выражений. Прошу прощения за высокомерный снобизм, но у вас просто нет достаточного опыта судить об удобстве записи в математике. Проблемы с записью особо громоздких конструкций есть, и они вполне себе решаются. К примеру, в ML вполне себе рисуют картинки вместо явной записи свёртки десятка тензоров с двадцатью индексами. В физике та же фигня: используют бра-кет запись, диаграммы и тому прочее наравне с обычной записью. Это всё есть (правильные и вполне рабочие) уровни абстракций.

    Ну а проблемы преподования — да, они есть. Универсального курса матана, идельного и понятного всем не существует. Преподователь, лектор или автор учебника обязан делать допущения относительно интересов аудитории. Во время курса он должен решать проблемы, знакомые его слушателям/читателям. А проблемы у всех нас разные. Поэтому и учебники и курсы разные: для математиков, для физиков, для химиков, для экономистов и т.п.


    1. akhalat
      09.11.2018 00:43
      #19342444

      Ну а проблемы преподования — да, они есть. Универсального курса матана, идельного и понятного всем не существует. Преподователь, лектор или автор учебника обязан делать допущения относительно интересов аудитории. Во время курса он должен решать проблемы, знакомые его слушателям/читателям

      всё-таки дело обстоит с точностью до наоборот. матан читают на самом первом курсе, когда у потенциальнах химиков, физиков, экономистов и прочих ещё нет никакого конструктивного понимания о проблемах своих наук (ну, кроме школьных представлений). кроме того, читают его на первом курсе не просто так. матан — по сути элементарный раздел математики, введение в математический язык. естественно, необходимо как можно скорее научить студентов этому языку, чтобы те как можно быстрее смогли понимать его внутри своих областей и пользоваться им для решения специализированных задач. это можно сравнить с элементарной азбукой, которой нужно овладеть, чтобы научиться читать, и как-то странно полагать, что для физиков, химиков или экономистов нужно каждому по специализированному букварю


      1. geisha
        09.11.2018 01:36
        #19342574

        всё-таки дело обстоит с точностью до наоборот. матан читают на самом первом курсе, когда у потенциальнах химиков, физиков, экономистов и прочих ещё нет никакого конструктивного понимания о проблемах своих наук (ну, кроме школьных представлений)
        Почему бы не предположить обратное: если юное дарование специально выбрало ту или иную науку, то оно имеет хоть какое-то представление о проблемах в области. Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.
        это можно сравнить с элементарной азбукой, которой нужно овладеть, чтобы научиться читать, и как-то странно полагать, что для физиков, химиков или экономистов нужно каждому по специализированному букварю
        ИМХО сравнение с изучением языка особенно точное (и мне оно нравится). Есть английские курсы для детей, для взрослых, для технарей, для китайцев и т.п. — каждому нужен свой подход, не смотря на то, что предмет один и тот же.


        1. akhalat
          09.11.2018 01:44
          #19342598

          Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.

          это нормально, но до того как приступить непосредственно к решению задачи, вам нужно изучить основы — которые абсолютно одинаковые для всего, они более элементарны и находятся над (или «под») этими задачами — отличная аналогия с кирпичиками выше
          потому что более-менее реальные задачи — это как минимум дифференциальные уравнения, которые идут далеко после курса матана
          каждому нужен свой подход, не смотря на то, что предмет один и тот же.

          да, язык может специализироваться потом, но база — она одинаковая во всех курсах: алфавит, произношение, времена (прошлое, настоящее и т.п.), основной набор начальных слов, формы глагола «to be» и т.д. когда база получена, начинается специализация с разучиванием конкретных тем и конкретных наборов слов для них, но базовая грамматика — везде одна
          также и с матаном, он даёт элементарную базу, которую потом уже используют в курсах физики, химии и прочего для решения конкретных задач


          1. geisha
            09.11.2018 02:36
            #19342714

            Я перестал вас понимать. Задача — это, к примеру, почему планеты движутся по почти замкнутым орбитам в плоскости. В формулировке нет никаких кирпичиков от матана в том смысле, что даже семиклассник сможет понять в чём вообще проблема. Ну а препод по матану может взять эту задачу на вооружение и рассказать о бесконечно малых, о рядах, о пределах, о производных и их разновидностях (что есть азбука матана) на примере этой задачи.

            Относительно языков — у вас явно нет положительного опыта. Я пытаюсь учить свой четвёртый язык и, на текущий момент, я ещё не знаю всех тонкостей алфавита, но могу спросить почём велик в магазине или какая сегодня погода. Да и всех форм «to be» я тоже не знаю. Заставить всё это учить до базовых фраз — это всё равно, что давать определение пределов по Коши и определение производной на первой лекции, а потом сказать, что tan' = 1/cos^2 следует очевидным образом, попутно заставив студентов заполнять таблицу производных дома. Да, это — последовательно и строго, но не имеет никакого отношения к обучению.


            1. akhalat
              09.11.2018 03:45
              #19342834

              ну смотрите, движение планет — второй закон ньютона. а что там у нас в правой части, dp/dt — производная. и — всё. чтобы дойти до этого надо начинать с последовательностей (на самом деле с вещественных чисел, ну ладно, их введем аксиоматически), потом пределы, обобщить пределы на функцию, ввести производные, потом дифференциалы, и наконец доказать теорему о постоянной функции (и то, это будет такой лайфхак, чтобы получить постоянную для движения, а по чесноку уравнения надо интегрировать, а это — пилить ещё больше семестра до определенных интегралов и формулы Ньютона-Лейбница) — итого больше чем полсеместра чистого матана. но на самом деле прикол в том, что параллельно матану у вас уже будет идти физика, где вы будете решать эту и много других замечательных задач и где от вас уже будут требовать в полной мере владения дифференциальным и интегральным аппаратом, только посмеиваясь над попытками школьных оправданий вроде «а по матану мы ещё до этого не дошли». на самом деле в этом нет ничего страшного, ибо дифференцировать и интегрировать учат в школе, но там именно натаскивают на решение типовых задач и ставят технику, а вот полного понимая теории и всех ньюансов у вас до курса матана не будет. так что приложением матана к задачам физики вы будете заниматься непосредственно в курсе физики, так как сама физика внезапно целиком и полностью написана на языке матана, а вот учить матан и восполнять школьные пробелы будет именно на парах матана.

              Я пытаюсь учить свой четвёртый язык и, на текущий момент

              не знаю какой язык, в изначальном сообщении вы упомянули английский вот давайте на нем и остановимся. «я ещё не знаю всех тонкостей алфавита» — серьёзно, какие тонкости алфавита? алфавит просто надо знать, 26 букв
              «Да и всех форм «to be» я тоже не знаю» — серьёзно, I am, he is, we are?
              «базовые фразы» — это My name is Vasya и London is the capital of Great Britain
              вы серьезно полагаете, что в какой-то методике изучения языка можно избежать знания такой элементарщины?
              хотя, конечно могут быть разные, в том числе и экзотические методы изучения языков — всё таки там простор для творчества почти не ограничен и аналогия с матаном всё-таки условная. в нём же широко не разгуляешь, т.к. есть очень жёсткая и последовательная логическая структура


              1. geisha
                09.11.2018 03:58
                #19342846

                Вы написали много, мягко говоря, противоречивых вещей. Я безоговорочно капитулирую в этом «споре». На вопросы отвечаю.

                какие тонкости алфавита?
                Я имел ввиду конкретно диактрику, которой в английском языке нет.
                вы серьезно полагаете, что в какой-то методике изучения языка можно избежать знания такой элементарщины?
                Нет.


        1. DaneSoul
          09.11.2018 19:52
          #19346296
          +1

          Почему бы не предположить обратное: если юное дарование специально выбрало ту или иную науку, то оно имеет хоть какое-то представление о проблемах в области. Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.
          Будущему инженеру или физику применение математики в его сфере вполне очевидно еще в школе. А вот даже олимпиаднику биологу места применения математики в его науке станут видны только ближе к концу обучения. Вот где химию применять в биологии да, понятно еще в школе, а вот то что многие процессы описываются сложными мат.моделями — это далеко не так очевидно даже очень увлеченному биологией школьнику.


          1. geisha
            10.11.2018 00:27
            #19347190

            Вы-то за всех биологов-олимпиадников не говорите. К примеру, можно сделать проект на конкурс, собрать данные, скажем, о распространении тли, обработать их, смоделировать что-то там и в процессе познакомиться с элементами из матана. Даже чтобы просто представить какой-то объем данных по любой дисциплине на красивом слайде может понадобиться матан. А статистика, которую в СНГ вообще не учат, на Западе (да и на Востоке) вообще считается маст-хэв для всех и учится в школе.

            Конечно, не имеет смысла говорить что прямо все школьники должны этим интересоваться. Но если интересуются — то это нормально, что я и написал.


            1. DaneSoul
              10.11.2018 00:44
              #19347212

              Вы-то за всех биологов-олимпиадников не говорите.
              А я за всех и не говорю, но знал реальные примеры реальных людей очень увлеченных биологией и с нулевой математикой и непониманием ее необходимости.
              Я тоже считаю статистику и основы теор.вера маст хевом и даже считаю что именно их надо изучать в школе для понимания очень многих жизненных вещей вместо интегрирования с диференцированием, которые все равно большинству из тех кто не пойдет в ВУЗ вообще никак в жизни не пригодятся.
              Но, из необходимости статистики необходимость матана кстати для многих совсем не очевидна до глубокого погружения в тему.


              1. geisha
                10.11.2018 01:42
                #19347308

                Вот эта фраза:

                А вот даже олимпиаднику биологу места применения математики в его науке станут видны только ближе к концу обучения
                звучит именно так, как будто вы говорите за всех. В любом случае, я не агитировал заставлять всех учить матан и не пойму, зачем вы вообще оставили ваш комментарий под моим. Речь шла о том, учить раньше или позже, ну так вот: я не вижу смысла откладывать тот или иной предмет по той причине, что некоторым он может не понадобиться. Это абсолютно неконструктивно. Так можно откладывать всё. Предметы идут по повышению сложности и матан — один из самых легких. Поэтому, его изучают на первом курсе. Всё.

                Вопросы о том, нужно ли его изучать в принципе можете обсудить с противниками высшего образования как такового. Я считаю, что высшее образование — вещь, по большому счёту, статусная (= необязательная), и если тебе этот статус не нужен — можешь самостоятельно учить то, что интересно и в любом порядке. Это как купить Феррари: ты же не будешь просить сделать салон из кожзама просто потому, что он дешевле? Если нужно дешевле — есть другие автомобили, а если хочешь Феррари — будь добр брать то, что продают и по той цене, которой продают. Так и с высшим образованием: либо иди и соответствуй, не задавая лишних вопросов, либо учи сам. При этом никто не исключает, что покупая фордик или штудируя онлайн курсы ты будешь счастливее, умнее, быстрее или успешнее чем если бы вбухал своё время/деньги в статусную вещь. Утрирую совсем чуть-чуть.


      1. Dr_Faksov
        09.11.2018 11:21
        #19343674
        +1

        Не математик. Читал недавно книжку, название (по памяти) «Идеи (или теории) которые должны умереть». Это сборник статетей участников некоего научного сообшества (не рускоязычного). В этой книге запомнилась статья про матан. Там два вывода: 1) Матан реально нужен ОЧЕНЬ маленькому числу учёных -ИССЛЕДОВАТЕЛЕЙ. 2) Бесконечная глупость читать матан на первом курсе.


        1. geisha
          09.11.2018 13:05
          #19344278
          +1

          Можно бесконечно растягивать и, соответственно, удорожать образование отодвигая предметы на потом. Не удивлюсь, если некое научное сообщество в этом прямо заинтересовано.


        1. msububble
          09.11.2018 13:43
          #19344438

          Посмотрите, пожалуйста, оно? www.labirint.ru/books/605779
          Если да, про ученых-исследователей в каких областях идет речь в соответствующем эссе?
          Чем ближе наука к практике, чем нужнее там математический аппарат, тем преступнее продавать такую книгу за деньги.


          1. Dr_Faksov
            10.11.2018 17:11
            #19348834

            Это оно. Мне очень понравилась. Кругозор развивет очень здорово.
            Я извиняюсь, сказано это было про подготовку програмистов. Основная идея — матан на первом курсе отсеивает кучу народа, убивая уверенность в собственных силах и отвращает от професии


            1. Maxim_Andreev
              10.11.2018 18:35
              #19349112

              Что характерно, книга написана учёными из США и Канады, где (как и в России) какая-то зашкаливающая доля людей с высшим образованием (т.н. Grade inflation). Если в стране «высшее образование» у 50% населения, этот уровень можно смело принимать за средний, а «высший» уровень присваивать тому меньшинству, которому для работы требуются сложные для освоения большинством методы (например, математика в случае технического образования).
              Тогда не будет таких проблем, что программиста пичкают матаном, потому что программиста будут учить в образовательных учреждениях среднего специального образования (как например, в немецкоязычных странах), и он будет справляться с большинством задач, которые сегодня решает средний программист.
              В ВУЗах же должны учить математиков, физиков и инженеров, для которых программирование является лишь одним из инструментов, который облегчает использование в своей работе математических методов.


              1. Dr_Faksov
                11.11.2018 06:17
                #19350342

                Не помню, кто сказал, что в ближайшие годы страны мира НАВСЕГДА поделятся на развитые и неразвитые. «Развивающихся» не будет. И перейти из неразвитых в развитые будет НЕВОЗМОЖНО (обратно — запросто). Те правительства, которые серьёзно относятся к будущему своих стран, прилагают все усилия чтобы мотивировать людей учится. За Штаты не скажу, а в Канаде в последние годы, во многих провинциях, для людей с низким доходом, высшее образование практически бесплатно. Правительство выделяет гранты на образование. Именно гранты а не ссуды.


  1. 0serg
    09.11.2018 00:26
    #19342400
    +4

    На мой взгляд математика — это наука о том как из отдельных «кирпичиков» складывать по определенным правилам большие «здания» доказательств. Математика принципиально «конструктивна» — мы не «разбираем» здание на кирпичики а строим его из них. При этом практическую пользу обычно несет именно «здание» а не «кирпичик» что и порождает нежелание возиться с «бесполезными кирпичами» которое Вы описываете. Поверх этого идет необходимость строить здание по строго определенным правилам. Что тоже порождает протест — почему это я не могу построить здание которое я хочу и как я хочу? Зачем мне эти дурацкие правила? Но вот без правил этих ничего толкового построить на практике, увы, не удастся. И хотя «общий обзор» возможных зданий куда интереснее, но, увы, толком не приближает нас к пониманию того как же эти здания надо строить.

    Демонстрация «общего» — это неплохой способ а) заинтересовать слушателя («о, какую классную вещь можно сделать») и б) дать ему в руки «кирпичик» большего размера (давайте будем собирать типовые хрущовки из панелей вместо того чтобы возиться с кирпичами"). Но и только. Вот писал я, к примеру, на Хабр статью про преобразование Фурье. Именно с позиций «рассказать об общей картине». И все бы хорошо — но это не математика. И если человек захочет серьезно разобраться в ПФ то ему все равно придется нырять в (зверски непростой и далеко не очевидный) матан. Моя же статья никак, увы, этому не учит. В лучшем случае — показывает как пользоваться ПФ в «бытовых» целях.

    Возвращаясь к вопросу «как учить математику»: у нас есть два компонента которым следует научить. Показать «кирпичики» и показать «правила» по которым они складываются а затем натренировать человека чтобы у него в памяти отложились а) список наиболее полезных кирпичиков, б) доведенные до автоматизма правила их складывания и в) типовые полезные чертежи которые легко можно адаптировать под конкретный частный проект дабы не делать его с нуля. Для чего мы берем студента и заставляем его а) учить список кирпичиков и правил и б) строить, строить, строить и еще раз строить на практике из них разнообразные дома. От простых к сложным — пока руку не набьет. Но это, собственно, ровно то как процесс преподавания математике сейчас и организован. По крайней мере в ФМШ и на мехмате МГУ где я учился. При этом простые задачи часто будут не интересные и скучные — условно говоря, «сложите из кирпичей колонну в два кирпича на два высотою 3 метра». Но это — работает. А вот попытавшись разок разобрать здание на кирпичики Вы вряд ли научитесь как его строить. Особенно при попытках разобрать здание сложное (а именно такие представляют наибольший практический интерес) — просто завязните в деталях или упустите массу важных моментов. Интересных задач в математике вообще не так уж много и руку только на них одних набить, увы, не получится.


    1. Oxoron Автор
      09.11.2018 01:45
      #19342600
      +4

      О, хорошая аналогия. Несколько риторических вопросов: сможет ли такой строитель разработать принципиально новый кирпич, если текущих не хватает? Насколько часто возникают ситуации, что текущих кирпичей не хватает? Кого запоминают больше: разработчиков новых кирпичей? Кто нужен чаще, укладчик стандартных кирпичей, или разработчик новых?

      Вопросы актуальные: если обзор каждого кирпичика позволит быстрее довести до автоматизма «правила складывания» — есть ли резон обозревать каждый кирпичик? Если обзор каждого кирпичика упростит процесс обновления знаний в будущем — есть ли резон обозревать каждый кирпичик?


      1. 0serg
        09.11.2018 11:09
        #19343606
        +5

        «Новые кирпичи» появляются исключительно редко, это по сути рождение целых новых областей в математике. Обычное математическое образование даже не ставит перед собой задачи создать людей способных на это. Но сила математики в том что сравнительно небольшого числа существующих кирпичиков хватает на громадный пласт практических и теоретических построений.


    1. third112
      09.11.2018 03:03
      #19342768

      Математика принципиально «конструктивна»
      Опасное утверждение в случае математики:
      Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения. Согласно критерию конструктивности — «существовать — значит быть построенным».[17] Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.[18] (Вики)

      (Мне показалось, что «Конструктивная математика» не имелась в виду? — Уточнил на всякий случай.)


      1. 0serg
        09.11.2018 11:05
        #19343588

        В любой математике доказательства конструктивны.
        Конструктивная же математика о которой Вы пишете (более правильное название — «математический конструктивизм») — это попытка обобщить эту идею дальше, потребовав чтобы не только доказательства но и объекты с которыми они оперируют строились конструктивно.


        1. Druu
          09.11.2018 11:14
          #19343642

          Ну вообще можно доказать, что доказательство существует, но само его не предъявлять :)


          1. 0xd34df00d
            09.11.2018 18:02
            #19345866

            Будет ли это формализуемым доказательством?


            1. Druu
              09.11.2018 21:42
              #19346656

              Это неоднозначный вопрос.
              Смотрите, если у вас есть конкретный вывод, то утверждение "вывод существует" (= "теорема доказана") не просто выводимо — оно явно истинно.
              Если же вы вывели утверждение о существовании вывода, не предъявляя самого вывода, то вопрос истинности, вообще говоря, еще открыт. Да, обычно у нас soundness и выводимое утверждение истинно в любой интерпретации, но что если нет? Допустим, метатеория противоречива — в этом случае утверждение о существовании вывода в теории может оказаться ложным. Ложной будет и теорема. Если же вы доказали теорему предоставив вывод — то теорема доказана вне зависимости от противоречивости любой метатеории.
              Так что, по логике, явно эти случаи должны быть разделены.


        1. ankh1989
          09.11.2018 12:26
          #19344052

          Готовое доказательство конструктивно в том смысле, что к выводу доказательства есть конечный путь из логических следствий начиная от определения «вещественное число это ...» Однако придумывание доказательства штука очень неконструктивная. Это скорее прохождение бесконечномерного лабирита в темноте. Конструкнивность это скорее про программирование: там именно собирают кирпичи вместе и делают конструкции совершенно офигительной высоты. Интуиция там как правило не участвует.


          1. 0serg
            09.11.2018 12:41
            #19344122

            Не, в программировании все примерно так же. Есть простые задачи, есть сложные. Путь решения к простым задачам находится легко и интуиции не требует (вплоть до возможности автоматизации поиска решения). Путь решения к сложным — нет.


            1. Druu
              09.11.2018 15:25
              #19345026
              +1

              Не, в программировании все примерно так же.

              И даже не примерно, а в точности в силу изоморфизма Карри-Говарда (типы — утверждения, термы соответствующих типов — доказательства).


    1. khim
      09.11.2018 17:29
      #19345678
      +1

      На мой взгляд математика — это наука
      Математика — это не наука. крите?рий По?ппера она проваливает с треском. Математика — это инструмент, которым пользуется наука. Любая. Много вы видели программистов, которым никогда не требовалось складывать строки? А ведь там нас ждёт Маляр Шлемиэль, пределы и O большое. Потому идея «не преподавать матан» заставляет задумать о том, являются ли авторы этой идеи вообще учёными или нет.

      Сила и слабость математики вообще (и матана в частности) — ровно в том, что это не наука, и стало быть, с реальными миром она никак не связана.

      А вот желания конкретного индувидуума — с реальным миров очень даже связаны… но у разных людей — разные цели. Потому очень сложно сделать самоучитель математики, которй был бы интересен всем.


      1. ganqqwerty
        09.11.2018 17:45
        #19345772

        Критерий фальсификации Поппера, на который начали молиться в постсоветское время — не единственный критерий научности в философии науки, и тем более, не самый лучший. Вы посмотрите на этот абсурд — математика по нему не является наукой, разве это не лучшая демонстрация несостоятельности самого термина «науки-по-попперу»?


        1. khim
          09.11.2018 18:24
          #19345980
          +2

          Вы посмотрите на этот абсурд — математика по нему не является наукой, разве это не лучшая демонстрация несостоятельности самого термина «науки-по-попперу»?
          Нет. Я хорошо помню курс «философия математики» и хорошо помню как там у самых разных философов были самые разные подходы — и у большинства математика «выпадала».

          Именно потому, что математика — не наука. Там невозможны эксперименты, там новые знания не могут ограничить область применимости старых и т.д. и т.п.

          Как тут уже писали: математика — это язык, на котором написана «книга природы», но к самой этой книге математика — отнощения не имеет.

          Это одновременно и самое сильное и самое ужасное свойство математики…


          1. Moskus
            09.11.2018 21:46
            #19346678
            +1

            Математика — способ описания явлений и связей между явлениями. Способ со внутренней структурой, которую можно проверять на целостность только относительно себя самой. Верность самой реальной связи между явлениями, например, не может быть подтверждена внутренней верностью описания этой связи. Скажем, математическая формула из ньютоновской механики не дает никакого намёка на более общую формулу из релятивистской механики, хотя и является ее вырожденным случаем.


            1. saboteur_kiev
              10.11.2018 01:59
              #19347322

              IMHO не явлений, а догм и аксиом.
              Явления это уже больше к физике.


              1. Moskus
                10.11.2018 12:47
                #19348102

                Вы, совершенно случайно, последнее предложение из моего комментария не пропустили? Похоже, что пропустили.


      1. 0xd34df00d
        09.11.2018 18:04
        #19345886
        -1

        Почему? Если относиться к эксперименту в математике как к синтаксической проверке абсолютно формального вывода искомого утверждения, например.


        1. khim
          09.11.2018 18:27
          #19345990
          +1

          Потому что эксперимент, в науке, предназначен для проверки наших знаний об окружающем мире. Математика ничего «не знает» об окружающем мире: аксиомы истинны по определению, а любые, сделанные на их основе выводы, либо абсолютно верны (если нет ошибок), либо, так же абсолютно неверны (если ошибки есть).


      1. Zenitchik
        09.11.2018 18:31
        #19346012
        +3

        Критерий Поппера предназначен для ЕСТЕСТВЕННЫХ наук.
        А общего критерия для всех наук — не существует.


        1. ganqqwerty
          10.11.2018 01:06
          #19347266

          Помню я спрашивал у нашего философа, является ли «Наука Логики» Гегеля наукой по Попперу. Только недавно понял, насколько неправильным был этот вопрос и насколько сильно мы инфицированы религиозным попперианством.


          1. khim
            10.11.2018 02:32
            #19347372

            Причём тут религоизность? Наука — это просто такая область деятельности, где мы строим часть картины мира на основе опытов. Всё. Это просто определение, не больше, не меньше. Вот прямо в первом абзаце: Нау?ка — область человеческой деятельности, направленная на выработку и систематизацию объективных знаний о действительности. А математика никаких знаний о действительности нам не даёт — ни объективных, ни субъективных, никаких! Какая ж это, нафиг, наука?

            Заметьте: это не означает что всем, что не наука, не нужно заниматься! Написание каких-нибудь романов и написания поэм, скажем, ни разу не наука ни по какому критерию — но жить в мире, где нет ни писателей, ни поэтов будет невыносимо скучно.


      1. Druu
        09.11.2018 21:50
        #19346696

        Математика — это инструмент, которым пользуется наука.

        Мы, вроде, с вами уже это обсуждали. В математике ученые формулируют утверждения вида: "из последовательности символов А при помощи последовательного применения правил преобразования Х можно получить последовательность символов В". Это вполне фальсифицируемо — просто берешь А, выполняешь указанные преобразования и смотришь, что получилось. Если получилось не В — утверждение сфальсифицировано.
        Никаких нефальсифицируемых утверждений в математике не формулируется.
        Вы, конечно, можете какие-то последовательности символов интерпретировать как некие утверждения, и эти утверждения, действительно, могут оказаться нефалльсифицируемыми. Только математика тут уже не при чем, это же вы интерпретациями занимались.


        1. roman_kashitsyn
          09.11.2018 22:17
          #19346816

          В математике ученые формулируют утверждения вида: "из последовательности символов А при помощи последовательного применения правил преобразования Х можно получить последовательность символов В".

          Это только в конструктивной математике. Вообще говоря, много утверждений вида "существует объект, обладающий свойством P" или, выражаясь вашими словами "как не крути правила X, последовательность B из A ты получить не сможешь" (обычно эти теоремы самые важные и сложные).


          Примеры:


          • У любого полинома n-степени с комплексными коэффициентами (n?1) существует хотя бы один комплексный корень (ни слова про то, как его найти).
          • Для любого n ? 5 не существует формулы, которая бы выражала корни любого полинома степени n в радикалах.
          • Всякое n-мерное многообразие гомотопически эквивалентно n-мерной сфере тогда и только тогда, когда оно гомеоморфно ей (когда я наконец понял разницу между гомотопиями и гомеоморфизмами, мне это крышу снесло).


          1. Druu
            09.11.2018 22:24
            #19346830

            Это только в конструктивной математике.

            Нет, это абсолютно в любой.


            Вообще говоря, много утверждений вида "существует объект, обладающий свойством P"

            Так это утверждение является просто последовательностью символов. Которую нам надо получить из другой последовательности символов (условий теоремы). В качестве доказательства теоремы — у вас конечная последовательность правил вывода, которые из последовательности символов, описывающей условия теоремы, делают последовательность символов, описывающих результат теоремы.


            Примеры:

            Ну и все ваши примеры — это те самые пары последовательностей А и В. А доказательства этих теорем — конечные последовательности правил, которые путем своего применения А превращают в В.


            1. roman_kashitsyn
              09.11.2018 22:35
              #19346858

              А доказательства этих теорем — конечные последовательности правил

              Нет, правила — это логика + набор аксиом. Доказательства — это последовательные применения законов логики к аксиомам для получения требуемого результата.


              Только вот в современной математике док-ва стали настолько сложными, что проверить их абы кто не может, нужны другие супер-математики. И даже если всё проверили, не исключена вероятность, что где-нибудь ошибка сидит. Воеводский не от хорошей жизни гомотопической теорией типов занялся.


              Когда-нибудь всё везде будет строго доказываться на аналоге Coq, вот тогда ваш тезис будет совсем верным.


              1. Druu
                09.11.2018 22:41
                #19346884

                Нет, правила — это логика + набор аксиом.

                Вы забыли про правила вывода. С-но аксиомы можно рассматривать как частный случай правил вывода с пустой левой частью. Законы логики — тоже состоят из аксиом и правил вывода.


                Только вот в современной математике док-ва стали настолько сложными, что проверить их абы кто не может, нужны другие супер-математики.

                А это ничего не меняет, фальсифицирующий эксперимент не перестает им быть от того, что его сложно провести. В итоге все равно у вас есть вывод, который можно формально проверить на валидность.


                1. roman_kashitsyn
                  09.11.2018 23:04
                  #19346958

                  Вы забыли про правила вывода.

                  Под "законами логики" я имел ввиду исчисление предикатов и логика высших порядков, о каких именно "правилах вывода" вы говорите? Мат. индукция? Это частный случай исчисления предикатов.


                  1. khim
                    10.11.2018 02:36
                    #19347378

                    Мат. индукция? Это частный случай исчисления предикатов.
                    Не совсем так. Исчисление предикатов может «покрыть» лишь счётный набор множеств. А в реальной науке часто приходится рассуждать о несчётных наборах.

                    То есть когда вы вот в том самом матане написали ?х?? — всё, вы вылетели за рамки «исчисления предикатов». Потому что оных ? — несчётное множество.


                    1. Druu
                      10.11.2018 09:35
                      #19347718

                      Не совсем так. Исчисление предикатов может «покрыть» лишь счётный набор множеств. А в реальной науке часто приходится рассуждать о несчётных наборах.

                      Нет, вы вполне можете рассуждать о несчетных наборах, проблема в том, что вы, неформального говоря, не сможете в явном виде "пощупать" более чем счетное подмножество этого набора. То есть вы можете говорить об R, можете говорить об элементах R, но если вы попытаетесь говорить об отдельных конкретных элементах R, как об отдельных числах, явно их обозначая — вот тогда и возникнет проблема.
                      Еще вы можете в теорию явно насовать все требуемые константы, но тогда у вас будет несчетная сигнатура.


                      1. khim
                        10.11.2018 18:36
                        #19349114

                        Нет, вы вполне можете рассуждать о несчетных наборах, проблема в том, что вы, неформального говоря, не сможете в явном виде «пощупать» более чем счетное подмножество этого набора.
                        Я — могу. А «исчисление предикатов» (вернее логика первого порядка) — не может.

                        Она оперирует с формулами, коих, как несложно понять, счётное число, а не с множествами — которых несчётно. Отсюда и знаменитая теорема.


                  1. Druu
                    10.11.2018 09:33
                    #19347716

                    Под "законами логики" я имел ввиду исчисление предикатов и логика высших порядков, о каких именно "правилах вывода" вы говорите?

                    И я говорю про исчисление предикатов (логика первого порядка). В ней два правила вывода — modus ponens и обобщение. Индукция (когда она содержится в аксиоматике) — это обычно аксиома (или схема).


                    логика высших порядков

                    Ну ей де-факто никто не пользуется (исключения есть, в пределах стат. погрешности).


    1. Dr_Faksov
      10.11.2018 17:14
      #19348846

      И тем не менее, проэктирования здания начинается с общего вида. Чертежи кладки кирпичей — много позже.


  1. Moskus
    09.11.2018 00:54
    #19342462
    +4

    Вопрос с «реальными проблемами» (прикладными, на самом деле) не так очевиден, как вам кажется.
    Если человек пытается вникнуть в суть абстракции, но у него никак не получается, и он ищет практический пример (являющийся, как это чаще всего бывает, в той или иной степени вырожденным случаем), а найдя его — удовлетворяется, у этого человека, вероятнее всего, просто недостаточно развиты навыки абстрактного мышления. Потому что вырожденный пример хоть и может иллюстрировать абстракцию, но не может ее полностью описывать (просто по определению). Уверенность в понимании, которая возникает после знакомства с такими примерами — ложная. Решение частных задач помогает укрепить понимание абстрактной концепции, на которой они основаны, то есть является хорошим упражнением, но не может заменить само понимание. Понимание возникает при анализе связей между частями абстракции, при попытках группировать фрагменты абстракции на основе этих связей, при попытках поиска связей. А не при мысленном сравнении и установлении тождества (операции конкретно-предметного мышления, а не абстрактного).


    1. ankh1989
      09.11.2018 12:32
      #19344074

      Это кстати интересный вопрос, о том как разные люди себе представляют математику. Вот например когда вы читаете про «компактное множество», что вы предствляете? Или например пространство интегрируемых по лебегу фукнций? Если в первом случае я вижу такую кучу непонятно чего с «чёткими» границами, то во втором случае это такая непонятная каша и честнее будет сказать, что я на самом деле никак это пространство не представляю.


      1. Zenitchik
        09.11.2018 14:30
        #19344700

        Хотел ответить, что я лично ничего не представляю. Но нет. Я представляю себе что-то вроде псевдокода. Каждая математическая сущность — это либо объект либо интерфейс (выражаясь в терминах ООП).


      1. Moskus
        09.11.2018 21:50
        #19346694

        В контексте владения абстрактным мышлением, это совершенно не важно, какой визуальный, слуховой или иной образ вызывает у человека упоминание той или иной концепции. Более того, этот образ может быть просто побочным продуктом мыслительного процесса.


    1. ganqqwerty
      09.11.2018 17:47
      #19345786

      Но если этих примеров он изучает много-премного, то он начинает замечать общее в них, что и приводит его к более глубокому понимаю самой абстракции.


      1. Moskus
        09.11.2018 21:20
        #19346574

        Вы проецируете математические операции на мыслительные. Это так, на самом деле, работает крайне редко. В смысле, это может так работать, но если человек способен проанализировать множество частных случаев и сделать верный вывод о механизме, он способен понять и абстрактное описание механизма. Если неспособен — ему ни то, ни другое не подходит.


        1. ganqqwerty
          09.11.2018 23:10
          #19346976

          Ну это вы как-то очень быстро сдались. Что значит неспособен? Неспособен — это значит, что преподаватель с неправильной стороны подошел.


          1. Moskus
            10.11.2018 12:45
            #19348098

            Вот тут я объясняю, что сходу винить только способ преподавания, исходя из того, что дисциплине, требующей высоко развитого абстрактного мышления — безосновательно. Не существует подтверждения, что высшую математику может успешно освоить и применять вне учебных условий каждый.


          1. Druu
            10.11.2018 13:14
            #19348186

            Неспособен — это значит, что преподаватель с неправильной стороны подошел.

            При чем тут вообще преподаватель? Учится-то не он, а студент. Если студент не научился, то это вина студента, у него же были абсолютно все возможности. Почему преподаватель виноват в том, что студент из-за своей лини не стал ими пользоваться?


            1. ganqqwerty
              10.11.2018 14:15
              #19348350

              Зависит от того, с какой вы стороны баррикад. Я вот со стороны преподавателей в основном и вижу, что образование работает на десятую часть своей возможной мощности. Раз я с этой стороны, я и фокусируюсь на том, что могу изменить.


              1. Moskus
                10.11.2018 22:39
                #19349694

                Это может прозвучать смешно в контексте этой дискуссии, но ваша точка зрения — по большому счету — марксизм, который делит всё на классы «угнетателей» и «угнетаемых». На самом деле, если даже точно известно, что преподаватель — идиот, это вовсе не означает, что все его студенты не понимают материал только из-за этого, а изменив подачу материала, можно их всех или даже просто какую-то часть вдруг сделать понимающими материал. Это ложная дихотомия уровня детского сада.


                1. ganqqwerty
                  10.11.2018 23:39
                  #19349868

                  Я не понял, где вы нашли это в моих рассуждениях. Конечно, факторов, по которым студенты не понимают материал много. Однако они отлично делятся на две группы — факторы, на которые я, преподаватель, повлиять могу, и те, на которые повлиять не могу. Подача материала и повышения качества преподавания — в первой группе, поэтому на них и надо лично мне сосредотачиваться.


  1. saboteur_kiev
    09.11.2018 00:56
    #19342468
    -5

    Миллион плюсов автору.


    1. ankh1989
      09.11.2018 12:32
      #19344078
      +5

      Тогда уж счётное множество плюсов.


  1. BugM
    09.11.2018 00:59
    #19342474
    +3

    Особенно за тервер обидно. Ну самая жизненная математика. От покера до рулетки с блекджеком.
    А на лекциях треш какой-то рассказывают. И люди потом не могут простейшие вещи на пальцах прикинуть.


    1. 0serg
      09.11.2018 09:33
      #19343302
      +2

      «Тервер на пальцах» дает опасно ошибочные построения. Там как раз очень легко ошибиться действуя исходя из здравого смысла и аналогий. Отсюда крайняя важность осознания там фундаментальных основ тервера и способности аккуратно их применять. Так что без трэша обойтись, увы, не получится.


      1. BugM
        09.11.2018 10:23
        #19343424
        +1

        Так из-за треша средний студент и не осваивает. Его пичкают непонятной теорией, вместо интереснейшего практичного знания.


        Нормальный студент такое забывает на следующий день после сдачи экзамена.


        1. 0serg
          09.11.2018 18:56
          #19346102
          +1

          Тервер имеет практическую ценность только когда он посчитан верно. От неверно посчитанного тервера как бы вреда не было больше чем пользы. А «без трэша» Вы в тервере черта с два что посчитаете правильно. Прикладной (да и не только прикладной) тервер вообще на мой взгляд печально славится уныло-скучными и порою зубодробительными выкладками которые надо проделывать правильно и аккуратно.

          Естественно это совершенно не означает что интересных задач на тервере не надо давать. Надо. Просто решать их как ни крути придется используя «трэш».


          1. BugM
            09.11.2018 19:05
            #19346138

            Я ровно про это и говорю. Сейчас начинают с очень сложно воспринимаемого, но зато точного определения. Продолжают еще более плохо воспринимаемой формулой. И заканчивают зубодробительными выкладками. А зачем и почему это все могут даже не сказать. Студенты все это забывают на утро после экзамена.

            А можно начать с объяснения и расчета кто из 3 игроков в русскую рулетку скорее всего умрет и каким игроком быть выгоднее всего. И уже продолжить формулами и строгими определениями используемыми для этих расчетов. Студенты все это скорее всего запомнят и поймут как и зачем применять.


            1. khim
              09.11.2018 19:18
              #19346184
              +1

              Студенты все это скорее всего запомнят и поймут как и зачем применять.
              Полезнее всего привести несколько примеров, где правильный ответ резко отличается от интуитивного (типа парадокса Монти Холла), показать что там всё отлично считается (если правильно считать) — и таки практика совпадает с теорией, а не со «здравым смыслом».

              Вот только точно ли всё это нужно пихать в учебник?


              1. BugM
                09.11.2018 19:25
                #19346214

                Да про те задачи что я говорю интуитивно тоже сложно сказать решение. На пальцах это не интуитивно, а посчитать примерно. На уровне больше-меньше и порядок разницы.

                Классические задачи? Конечно надо.
                Реальные задачи для которых все это и было придумано? Конечно надо.

                Учебники пишутся для живых людей. Живому человеку очень сложно воспринимать формальный текст. Лекторы бывают разные. Лучше подстраховаться и написать.


                1. Moskus
                  09.11.2018 22:00
                  #19346738

                  А тут уместен вопрос к методу.
                  Действительно ли все те, кто не понимают абстрактное объяснение, способны вообще понять эту концепцию до уровня свободного ее применения? Может так быть, что какие методы обучения не применяй, только те, кто особенно способен к абстрактному мышлению (меньшинство) способны это понять и использовать. А остальным стоит ограничиться эмпирическим применением прикладных шаблонных решений и умением верно выбирать из этих шаблонов. Вместо того, чтобы всех пытаться тянуть к высшему уровню, а когда они плохо тянутся — винить лектора, а не их самих за неверный выбор программы обучения, например.

                  Никого же не удивляет, что одни люди идут заниматься наукой и становятся учеными, а другие ограничиваются инженерией, то есть чисто прикладным применением. Это нормально, и для этого, в общем случае, есть все средства. Основная проблема — в том, чтобы как можно раньше понять, что больше подходит тому или иному индивидууму и концентрировать на этом усилия. А не растрачивать их на одних, тормозя других.


                  1. ganqqwerty
                    10.11.2018 14:30
                    #19348388
                    +1

                    Это разделение людей на сорта очень преждевременно. Давайте мыслить как исследователи. Попался вам такой ученик у которого «плохо с абстрактным мышлением». Мы ведь можем если не измерить, то хотя бы прикинуть, в каких местах у него возникают проблемы в абстрагировании? По-моему, можем.

                    • Он не понимает, что общего у трех сосен, трех лисиц и трех тюбиков зубной пасты? Ему неясно понятие числа? Ничего страшного, многие этого не понимали много лет, но сейчас большинство людей это освоило.
                    • Он не понимает, что общего у футбольного мячика и купола церкви, ему неясно понятие формы? Это тоже лечится.
                    • Он не понимает определение предела или неподвижной точки или компактного множества? А вы, как учитель, способны положа руку на сердце утверждать, что если вас с ним запереть на неделю в комнате, он все еще его не поймет?
                    • он не способен держать в голове длинные цепочки рассуждений? Ну дык, а какой его предел — два звена цепочки, пять? Можно ли помочь ему дорасти с пяти звеньев до шести?

                    Моя задача как учителя — понять, в какой момент ученик не справляется с тем, чтобы отбросить ненужное, сосредоточившись на общем. В какой момент его мыслительная машина заклинивает? В каком месте в ее механизме лежит камушек, как его вытащить? Очень часто бывает, что после преодоления затыка ученик начинает прямо-таки блистать — оказывается, что у него не общий «уровень абстрактного мышления» (ох уж и заносчивое словосочетание!) был низок, а просто была одна конкретная проблема с пониманием одной конкретной важной штуки.


                    1. Moskus
                      10.11.2018 22:47
                      #19349724

                      Все ваши утверждения о «это все поправимо» — о сферическом коне в вакууме. То есть ваше стремление все поправить — необходимо. Но не существует никакого, ни практического, ни теоретического доказательства или объяснения, как и почему это возможно в отношении каждого конкретного индивидуума, да еще и уже практически взрослого. Существуют системы образования, где индивидуальным особенностям уделяется на порядок больше внимания, чем в других системах (например, это финская система). Но даже в них основная часть проходящих через эту систему все равно остаются на довольно среднем уровне. Основной результат применения таких систем — уменьшение левой части распределения (сдвиг в среднюю, сведение к минимуму тех, кто раньше считался вообще неспособным к обучению), а не уменьшение средней в пользу правой. Правая остается практически столь же мала, как была.

                      В констатации факта, что не каждый может стать ученым, нет абсолютно ничего оскорбительного. Люди не рождены и не вырастают равными. Утверждение обратного — идеология, которая не основана ни на каких реальных научных фактах.


                      1. BugM
                        11.11.2018 00:19
                        #19350004
                        +1

                        Вузовская математика нужна не только ученым. Она нужна инженерам (в самом широком понимании этого слова), экономистам, биологам, химикам. Да в общем всем негуманитариям.

                        Система образования плохо выполняет эту функцию. И это точно можно улучшить. Как минимум сняв барьер «Я не понимаю зачем все это вообще нужно?»

                        Исходные данные у нас неплохие. Приходят люди неплохо сдавшие достаточно сложный ЕГЭ по математике. То есть они как минимум не тупые и мотивированные на обучение. Надо им помогать, а не ставить стену из непробиваемых определений.


  1. Arris
    09.11.2018 01:08
    #19342506
    +8

    До сих пор страдаю. Интеграл. Не умею. До сих пор.

    Матмех СПбГу, 97 год.

    — Совершенно очевидно, что… <.....> Ч
    Через 20 слов я уже совершенно перестаю понимать о чем речь и переспрашиваю:
    — Вы не могли бы объяснить…
    — Не мог бы. Это вам должны были рассказывать на алгебре. Что, не рассказали? Спросите преподавателя. Кто у вас препод? Имярёк? Ааа… — глубокомысленно, — понятно.
    Прихожу к преподу по алгебре.
    — Вы не могли бы объяснить…
    Препод поднимает на меня больные усталые похмельные глаза и сипло отвечает:
    — Не мог бы. Читайте учебник, там все есть.
    — Но я не понимаю, объясните пожалуйста.
    — Если вы не понимаете учебник, зачем вы поступали?


    Стыдно сказать, но в аналитическом виде я брать интегралы не умею до сих пор. В цифровом виде — столбиками, трапециями, кривыми — сколько угодно (еще в 8 классе умел). Ну ок, 20 лет этого не делал, но там же просто все…

    Но в аналитическом виде — для меня это реально тёмный лес. Какие-то фундаментальные основы, какой-то кирпичик выпал — и здание математики держится на честном слове.

    :(


    1. mayorovp
      09.11.2018 10:52
      #19343536
      +8

      Взятие интеграла в аналитическом виде — это набор трюков, а не теория. Тут надо не понимать, а практиковаться.


    1. Whuthering
      09.11.2018 11:44
      #19343806
      +1

      Жизненно. Очень жизненно. Прям слово-в-слово как у нас было.


    1. ankh1989
      09.11.2018 12:38
      #19344110
      +4

      Там всё просто как раз. Первое что надо знать: никто не знает как считать интегралы в аналитическом виде. Есть несколкьо известных приёмов: ну там «взять интеграл по частям», «угадать первообразную» и т.д. Интеграл берётся так: пробуем применить приём 1 — не работает, приём 2 — не работает, приём 3 — работает, применяем, повторяем. Это как собирать кубик рубика: никто (ну кроме тех кто постиг дзен) не знает как его собирать, но есть 5-6 известных трюков и их более-менее методом тыка применяют пока кубик не соберётся. Я бы ещё сравнил это с прохождением лабиринта: вы примерно предствляете куда хотите попасть, но не знаете как. У вас каждый раз есть несколько вариантов: идти вправо, влево и т.д. Вы эти варианты перебираете пока не найдёте выход или пока не надоест (возможно выхода нет — это «неберущийся» интеграл, и таких большинство).


    1. Druu
      09.11.2018 15:30
      #19345044
      -1

      Препод поднимает на меня больные усталые похмельные глаза и сипло отвечает:
      — Не мог бы. Читайте учебник, там все есть.

      Так все верно говорит. Вот возьмем человека, который на гитаре играет — вас же не удивляет, что нельзя просто прочитать какой-то хитрый самоучитель и стать хорошим гитаристом? Надо практиковаться, ежедневно, на протяжении многих лет. И если что-то не получается — значит, надо идти и заниматься соответствующими упражнениями. Тут все то же самое, вы когда к преподавателю приходите и говорите "я учебник прочитал и не понял", то тут вывод один — вы хреново читали, значит, надо читать еще. Один раз, второй, пятидесятый. Почитайте с недельку, рано или поздно дойдет.


      1. Arris
        09.11.2018 21:21
        #19346578
        +1

        вас же не удивляет, что нельзя просто прочитать какой-то хитрый самоучитель и стать хорошим гитаристом


        Не удивляет. Но, по вашей логике, получается так:

        Вы приходите в музыкальную школу на класс гитары и говорите преподавателю:
        — У меня не получается играть, помогите мне.
        А он вам в ответ:
        — Читайте учебник, там все есть. Если вы не понимаете, что там написано — зачем вы сюда поступали.


        И это хреновый преподаватель. Потому что хороший скажет:

        — Бери гитару и показывай, как ты играешь. Нет, пальцы не так ставишь. Смотри как надо. Держи. Попробуй сам. Вот так. Нет, не так, левее, крепче держи, ага. Теперь другая рука. Теперь давай еще раз повторим. Видишь, начало же получаться?


        К сожалению, методика «кинь его в воду и пускай пытается выплыть, а утонет — да хер бы с ним» крайне плохо работает, особенно для ментальных дисциплин.


        1. Druu
          09.11.2018 21:55
          #19346714

          Не удивляет. Но, по вашей логике, получается так:

          Нет, не так. В математике чтение учебника — это и есть выполнение упражнений (в том числе). По-этому отправить читать учебник — это равносильно тому, что преподаватель по гитаре покажет набор упражнений и отправит вас домой их выполнять.


          Нет, пальцы не так ставишь. Смотри как надо. Держи.

          И, опять же, в учебнике в виде доказательств теорем вам как раз и дана идеальная расстановка. Смотрите и учитесь сколько угодно.


          Потом вы придете на практическое занятие, попробуете там что-то подоказывать — и вам как раз расскажут, что вы "руки ставите неправильно" (если неправильно).


          К сожалению, методика «кинь его в воду и пускай пытается выплыть, а утонет — да хер бы с ним» крайне плохо работает, особенно для ментальных дисциплин.

          Ментальные дисциплины изучаются точно так же как нементальные — путем тренировки.
          Просто люди ленивы и трудиться не хотят, а хотят серебряной пули, какого-то фантастического текста, который прочитал — и все понял!
          Нет, в математике "понял" — это результат той самой тренировки. Понимание — это не знания, это навык. А с навыками все просто: no pain — no gain. Никакого способа считерить нет, как бы лентяям ни хотелось.


          1. roman_kashitsyn
            09.11.2018 22:26
            #19346832

            В математике чтение учебника — это и есть выполнение упражнений

            Нет.


            Я прочитал много книжек по математике и программированию, и совершенно уверен, что просто чтение не работает, в голове не остаётся совершенно ничего.


            Кмк, лучше всего начинать сразу с задач, и читать учебник, чтобы понять в чём заключается проблема и как её решить.
            Недавно пробовал такой подход с топологией. Берёшь задачи-теоремы, которые нужно доказать, и читаешь ровно столько учебника, сколько нужно, чтобы всё доказать/решить.


            Вот тогда реально хорошо понимаешь материал.


            1. Druu
              09.11.2018 22:31
              #19346846

              Я прочитал много книжек по математике и программированию, и совершенно уверен, что просто чтение не работает, в голове не остаётся совершенно ничего.

              Так надо не просто читать а разбирать текст. Естественно, по принципу "смотрю в книгу — вижу фигу" результат будет нулевой. Надо усилия прикладывать. Чтобы мышцы росли, надо брать вес, который даст стресс вашим мышцам. Иначе они расти не будут. Тут то же самое.


              Кмк, лучше всего начинать сразу с задач, и читать учебник, чтобы понять в чём заключается проблема и как её решить.

              Как именно вы будете работать с текстом — это уже ваше дело. Как удобно — так и работаете, это личное.


              Берёшь задачи-теоремы, которые нужно доказать, и читаешь ровно столько учебника, сколько нужно, чтобы всё доказать/решить.

              Только обычно до чтения соответствующей главы даже формулировка этих задач будет вам непонятна. Т.к. в них будут входить неизвестные термины. Смысл тогда эти задачи читать?


    1. ganqqwerty
      09.11.2018 17:51
      #19345806

      этот ваш махмет — это ж вроде игра на выживание, совершенно адские условия естественного отбора, чтобы из миллиона прошедших его дятлов, выпустились один-два Колмогорова.


    1. Arris
      09.11.2018 21:26
      #19346604

      Мда, только час ночи может быть мне оправданием за это:

      больные усталые похмельные глаза

      взгляд, конечно же взгляд! Больной, усталый и похмельный взгляд.


  1. samsergey
    09.11.2018 02:52
    #19342752
    +1

    Тут, мне кажется, всё просто: непонятно на лекции — спрашивайте преподавателя, непонятно после лекции — идите в библиотеку, непонятно в книжке — меняйте книжку, ищите статьи и первоисточники. Читайте зарубежные учебники (не потому что они лучше, а потому что они все разные). Сами устраивайте семинары среди студентов. Ставьте собственные задачи. И очень скоро вы поймёте: это вам вообще надо? У вас не будет потребительского отношения к математике, если она часть вашей жизни. Люди творили математику в войну, в голод, в юности и в старости, даже в психушке. И вовсе не из-за пользы, а потому что это была их жизнь, их понимание прекрасного. Таких всегда немного. Эйлеры, Гильберты, Фихтенгольцы, Фейнманы и Савватеевы всегда дефицит. И наконец, математика никому ничего не должна. Она не должна быть полезной. Не должна быть понятной. Только непротиворечивой. Её результатами можно пользоваться, и опыт показывает, что практически всё от абстрактных алгебр до теории кос, паркетов или категорий находит своё применение. Причём, не по отдельности, а в совокупности. Забавно наблюдать, как народ, ожидая год от года появления новых технологий, усиления мощности смартфонов, развития интеллектуальных сервисов, капризно возмущается: "Зачем нам все эти сложности с функциональным программированием — оно не практично, с коллайдерами — они дорогие и бесполезные, с теорией категорий и гомологической теорией типов — очередная фигня, которую понимает полторы сотни человек… эллиптические кривые, abc-гипотеза, вы что серьёзно считаете, что на них можно потратить жизнь?" Так что, по-моему, нет какой-то "проблемы современных математических текстов", которую можно было бы решить., как нет, скажем, "проблемы современного театра (потому что я в нём ничерта не смыслю)".


    1. third112
      09.11.2018 03:36
      #19342826
      +1

      Так что, по-моему, нет какой-то «проблемы современных математических текстов»
      ИМХО есть принципиальные проблемы. Кратко для примера можно назвать 3:
      1) Многие авторы отмечают тенденцию к усложнению доказательств новых теорем — есть опасение, что скоро появятся задачи, которые будут нерешаемы по причине сложности для любого человека (слишком сложные тексты);
      2) Системы ИИ автоматического доказательства теорем пока справляются только с тривиальными задачами. Ни одному математику не удается научить (сделать текст для) ИИ делать нетривиальные доказательства. Есть опасение, что не удастся.
      3) Машинное решение задачи 4х красок (текст) остается непонятным для математиков. Это методологическая проблема: можно ли в принципе признавать такое решение?


      1. samsergey
        09.11.2018 03:43
        #19342832

        Перечисленные вами проблемы, действительно реальны, важны и интересны, но обсуждаемая статья, к сожалению, не про них.


        1. third112
          09.11.2018 03:53
          #19342842

          ИМХО заголовок про них, а в статье сказано:

          размер текстового поля не позволил закончить выкладки

          т.о. полагаю, что автор до них просто не добрался, написав только о проблемах студентов младших курсов.


      1. ankh1989
        09.11.2018 12:57
        #19344204

        2) И не надо. Точно также у нас нет ИИ который бы мог написать программу, однако есть методы написания программ которые позволяют глупым человекам собирать необозримые по сложности программы. Например линукс можно было бы сравнить с библиотекой томов того самого Тейхмюллера, т.е. никто даже близко не пытается разобраться во сём досконально, как это делают с проверкой доказательств. Однако ни у кого не возникает вопросов работает линукс и есть ли там фундаментальные ошибки которые делают его неработоспособным. Когда я учился в универе, я попробовал записать доказательство простой теоремы в виде программы: ну там каждая лемма это функция и т.д. Не получилось потому что все «строгие» математические определения на самом деле не такие уж строгие. Типичный пример: «Рассмотрим множество функций A.» Нормальная фраза для математика, но совершенно бессмысленная для программиста. Какое множество? Конечное? Открытое? Счётное? Какие функции? Любые? Интегрируемые? Непрерывные? Сколько аргументов у них? Какого типа аргументы? Математики такие подробности всегда пропускают, потому что подразумевают контекст. По этой же причине «теорию тейхмюллера» проверяют уже много лет: автор подразумевает контекст, а другие математики пытаются догадаться, что там подразумевалось.


        1. khim
          09.11.2018 17:39
          #19345740

          Точно также у нас нет ИИ который бы мог написать программу, однако есть методы написания программ которые позволяют глупым человекам собирать необозримые по сложности программы.
          К сожалению все эти методы работают только если мы миримся с тем, что результирующая программа будет с ошибками и иногда будет делать не то, что нужно.

          Для математики такое не подходит.

          Однако ни у кого не возникает вопросов работает линукс
          Именно так. Ни у кого никаких вопросов не возникает ибо всем прекрасно известно: не работает. Вопрос только в том, что некоторые люди могут «завалить его» за пару дней, а некоторым потребуется неделя.

          Но завалить его могут все — тут даже вопросов нету.

          Математики такие подробности всегда пропускают, потому что подразумевают контекст.
          Да — это известная беда.

          Какое множество? Конечное? Открытое? Счётное? Какие функции? Любые? Интегрируемые? Непрерывные? Сколько аргументов у них? Какого типа аргументы?
          Это всё вопросы, на которые для каждой теоремы можно ответить. И, более того, сложность многих теорем варьируется от тривиальных до многотомно-доказываемых в зависимости от ответа на эти вопросы.


        1. 0xd34df00d
          09.11.2018 18:06
          #19345894

          Когда я учился в универе, я попробовал записать доказательство простой теоремы в виде программы: ну там каждая лемма это функция и т.д.

          Ну, математики однако ровно так и делают на всяких там коках-агдах.


        1. Druu
          09.11.2018 22:03
          #19346758
          +1

          Типичный пример: «Рассмотрим множество функций A.» Нормальная фраза для математика

          Какие-то у вас странные математики и странная математика. В моей математике всегда указывается, что это конкретно за множество.


  1. Tyusha
    09.11.2018 02:55
    #19342756
    -3

    Ужасный текст. Какие-то обрывочные мысли. Случайные примеры. Ничего не понятно. Неужели вы преподаёте?!


  1. basilbasilbasil
    09.11.2018 03:25
    #19342808
    +3

    Ну, набежали…
    Вот обьяснили предел на пальцах, бОльшее количество студентов быстрее поняло. Кому от этого стало хуже? При этом строгое определение никуда не делось.


    1. Druu
      09.11.2018 10:59
      #19343568
      +2

      Так на пальцах определение очевидное, его все сразу понимают. Проблема именно в использовании формализма, который довольно искусственен.


  1. LonerD
    09.11.2018 04:09
    #19342862

    А у нас на матанализе было всё просто. Пришёл преподаватель — и давай строчить на доске формулы. Понимание, примеры — не, не слышали. Да чего ж тут непонятного? всё очевидно… С трудом удавалось поспевать за ним хотя бы переписывать хотя бы текст (то есть мне удавалось поспевать… многие и на этом сдувались), а дома уже строчка за строчкой нужно было разбираться (конспекты получались удобные — сама суть без лишних слов). Мужик молодой был и невероятно головатый (сейчас он уже зав.кафедры стал), ещё и брат у него такой же… Ему всё казалось очевидным и даже не представлял, что кому-то что-то может быть непонятно. И требовал на экзаменах неплохо так (причём не денег, а именно знаний). Хотя итоговую оценку на третьем курсе (которая пошла в диплом) всем поставил автоматом.


    1. Dr_Faksov
      10.11.2018 17:23
      #19348866
      +1

      Самый класс, когда препод-математик в конце пары отходит в конец аудитории, задумчиво смотрит на исписанную доску и говорит: «А знаете, все что я сегодня расказал -неправильно. А как правильно — расскажу на следующем занятии.» В моей жизни такое было


  1. bodya
    09.11.2018 05:30
    #19342938

    «Математика. Утрата определённости» (англ. Mathematics: The Loss of Certainty) — Мо?рис Клайн (англ. Morris Kline)
    https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0._%D0%A3%D1%82%D1%80%D0%B0%D1%82%D0%B0_%D0%BE%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D1%91%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D0%B8


    1. bodya
      09.11.2018 05:47
      #19342948
      +2

      «Книга природы открыта перед нами, но написана она на языке, который мы понимаем не сразу, а лишь после того, как ценой немалых усилий и страданий с любовью выучим его. Язык этот — математика»


  1. alex103
    09.11.2018 07:22
    #19343054
    +3

    (немного юмора)

    Попросил однокурсника о помощи с вычислением длины кривой через интеграл. Тот взял бутылку пива, нарисовал рандомную кривую, спрямил бесконечно малыми отрезками...


    и всё это — бутылкой пива!
    :)


  1. maisvendoo
    09.11.2018 07:36
    #19343080
    +2

    Я не знаю, можно ли массово использовать подход общий обзор => контрпримеры => формализм.

    Можно. В своих дисциплинах я так и делаю. Но коллеги, преподающие смежные области и обеспечивающие мои дисциплины базой — в большинстве своем так не делают. К сожалению


  1. Refridgerator
    09.11.2018 08:07
    #19343114
    +4

    Добавлю нытья. Очень часто кажется, что некоторые математики специально запутывают свои тексты, чтобы менее сведущему в математике человеку было сложнее разобраться.

    Приведу конкретный пример. Пишу библиотеку для вычислений с повышенной точностью и дошла очередь до вычисления логарифмов. Поиск в интернете вывел на статью «A New Method for Approximating Logarithms with k-th Order» (pdf) — но даже после 20 прочтений так и не смог ничего понять. Там вводятся леммы, доказываются неравенства, даже есть глава с названием «The Algorithm», но вот самого алгоритма с формулой, где слева — логарифм, а справа — вычисления, обнаружить не смог. В конце там есть таблица с результатами и упоминается MATLAB, посредством которого сделаны вычисления, но самого кода — нет. Им что, жалко? Мне попадались работы, где код на фортране занимал больше места, чем математическое описание, и за такие работы отдельное спасибо авторам (хотя код у математиков обычно получается не очень) — как минимум его можно отдебажить и понять суть хотя бы алгоритмически.

    И ладно если бы я был дебил — но в итоге, плюнув на всё, смог вывести алгоритм вычисления логарифма самостоятельно (и это не метод Ньютона). И даже после этого я не смог до конца понять ту работу — в частности, откуда ограничение в r??, и почему m должно быть обязательно целым — т.к. у меня и с нецелым всё прекрасно считается.


    1. serkuznec
      09.11.2018 16:44
      #19345468

      некоторые математики специально запутывают свои тексты, чтобы менее сведущему в математике человеку было сложнее разобраться


      В ходе изучения нескольких математических дисциплин пришёл к тому же выводу. К сожалению, в реальной жизни, гений и злодейство — вещи вполне совместимые.
      1) Некоторые искренне не понимают — что тут такого может быть непонятного.
      2) Некоторыми движет некоторый «научный» снобизм: Я в свое время поломал над этим голову, постиг, так сказать, всю глубину наших глубин, а теперь поломайте голову вы. Этакая математическая «дедовщина».
      3) Случай описанный вами самый щепетильный: вопрос научного первенства и признания. Когда человек намеренно запутывает свой текст, не даёт всех выкладок, это говорит о том что он боится так называемой «кражи идеи», когда основываясь на его научном материале посторонние создают себе имя в научном мире («забывая» при этом упомянуть того кто проделал первоначальную черновую работу).

      PS Вообще было отвратительно узнать, что среди математиков были склоки не хуже чем травля генетиков во времена лысенковщины.
      http://cyclowiki.org/wiki/Пощёчина_Колмогорова_Лузину


      1. da0c
        09.11.2018 19:43
        #19346266
        +1

        Вставлю пять копеек про научные статьи в ответ на комментарии выше, и на утверждения ТС в конце публикации о том, что

        большая часть виденных мною «профессиональных» работ в плане подачи материала не отличается от учебников.

        Приведу выдержку о том, как принято доносить информацию до читателя в высокорейтинговых статьях.
        Treat the reader as you would a guest in your house. Anticipate their needs: would you like something to drink? Something to eat? Perhaps now, after eating, you’d like to rest?

        — Относитесь к читателю вашей работы как к гостю в вашем доме. Спросите, чего угодно гостю, может быть что-то выпить или перекусить? Не угодно ли гостю отдохнуть?
        Вот источник целиком — billf.mit.edu/sites/default/files/documents/cvprPapers.pdf
        Мне он в свое время очень помог начать писать хорошие статьи.


  1. DS28
    09.11.2018 08:13
    #19343128

    Нам препод по диффурам рекомендовал попробовать Уолтера Рудина читать, если Фихтенгольц не идёт. Кое-что действительно становилось понятнее…


  1. AlexMal
    09.11.2018 08:56
    #19343190
    +11

    Как вы думаете, стоит ли на хабр написать цикл статей, что-то типо «Курс Математического Анализа для программистов» с использованием примеров и практики?


    1. DelphiCowboy
      09.11.2018 09:05
      #19343220
      +1

      Да, было бы отлично!


    1. Whuthering
      09.11.2018 11:45
      #19343820
      +1

      Да. Подобного очень не хватает.


    1. gohan
      09.11.2018 23:13
      #19346986
      -2

      Можно, только если они будут грамотно написаны (без несуществующих в языке слов типа «типо»).


  1. andyudol
    09.11.2018 09:26
    #19343282
    +1

    Предствьте себе, что у вас есть СУБД. Вы хотите понять, как она работает. Но в вашем распоряжении только содержимое базы данных. Возможно, основываясь только на них, понять, как работает СУБД, как взаимодействует с другими программами, зачем вообще нужно всё это хозяйство? Нет.
    Так и с преподаванием математики. Это попытка скопировать данные из головы лектора в головы студентов. А у них и структура-то совсем другая, несовместимая.


  1. akryukov
    09.11.2018 09:33
    #19343300
    +1

    Когда я изучал высшую математику в универе, то активно пользовался сайтом mathprofi. Изложение довольно доступное и примеры понятные.


  1. AAngstrom
    09.11.2018 09:38
    #19343314
    +4

    Не отрицая наличие проблем в российской системе образования, хочется заметить следующее. У подхода с разжёвыванием материала по математике до мелкодисперсной массы, которую можно вводить через трубочку, есть проблема: для абстрактных и сложных понятий можно придумать десятки объяснений «на пальцах» и десятки примеров. И то, которое покажется ясным одному студенту, другого может поставить в тупик. Суть в том, что любой пример описывет только один какой-то аспект рассматриваемого понятия, и никто не знает, какой именно аспект будет непонятен очередному студенту. Это не говорит о том, что приводить примеры и давать упрощённые объяснения бесмысленно. Да и не вспомню я ни одного курса, где бы препы не давали бы примеров. Это говорит о том, что без обратной интерактивной связи со стороны студентов (которая вообще отсутствует, если речь идёт о книге) преподаватель может даже не знать, чего именно им не понятно.

    Тут мы подходим к другой проблеме. Человека невозможно научить. Но человеку можно помочь научиться. Иными словами, никакого другого обучения, кроме самообучения, не бывает. Универ, просто, сильно упрощает этот процесс тем, что там есть программа, которая, если выстроена разумно, даёт представление о том, в какой последовательности надо изучать предметы. И там есть люди, которые (предположительно) являются специалистами в своих областях и могут ответить на большинство вопросов. Но если студент сам не будет продумывать материал, хотя бы для того, чтобы сформулировать конкретные вопросы (примеры, контрпримеры и т.п.), то можно какие угодно суперучебники писать, какие угодно суперпедагогичные лекции читать — всё будет бестолку. В России, к сожалению, школьное образование построено так, что он приучает к тотальному контролю сверху, когда за тебя уже всё решили, тебе надо только как попугаю всё повторить. Это, естественно, мало способствует формированию правильных навыков самообучения. Однако, в хороших вузах как раз и пытаются эти навыки привить. Хороших вузов, только вот, мало…


    1. ganqqwerty
      09.11.2018 20:45
      #19346478

      Вы упускаете момент доверия к авторитету. Университетское образование рассчитано на то, что всякий приходящий в институт сознательно и подсознательно верит в авторитет университета и его преподавателей — именно это склонение перед авторитетом может позволить ему, скажем, не сильно задумываться о том, а действительно ли нужно интегральное исчисление будущему программисту. «Это не мое дело — подвергать сомнению программу, ее писали очень умные люди, а мое дело — прилежно ее изучать. Чем лучше изучу, тем лучшим я буду специалистом».

      В современном мире я очень сомневаюсь, что у нас есть такой высокий уровень доверия.


      1. Zenitchik
        09.11.2018 21:14
        #19346544
        +2

        Ну, это проблемы отдельно взятых студентов. Разумный подход (который, к сожалению, возникает после): учи пока преподают, всё, что изучишь — можешь когда-нибудь применить, или не применить, а то, что не изучишь — точно никогда не применишь.
        Я, вот, очень жалею, что слаб в математике.


        1. ganqqwerty
          09.11.2018 23:21
          #19347012
          +1

          Вот у меня была такая проблема — я всегда старался распределять свои силы разумно, всегда задавал себе вопрос «а зачем тебе заниматься вот этой дисциплиной?», и в свои 18 лет уж точно знал, что могу себе расставить приоритеты. Понимаете, я чувствовал себя сознательным индивидом, а не наивным ботаном!

          Каково же было мое удивление через семь лет после выпуска из института, когда я понял, что был я тупым кретином, который не доверял программе обучения из идиотского нон-конформизма замешанного на мутных суждениях типа «раз это государственный институт — то все там неэффективно и устарело», «мы живем в эпоху перемен, и что было верно вчера не будет верным даже сегодня» и коронное «я пришел программировать зергов, а вы мне тут показываете каких-то дурацких ферзей». За эти семь лет мне успела пригодиться почти каждая из дисциплин, и каждую пришлось заново самостоятельно изучать. Оказывается, тупые ботаны, положившиеся на авторитет зарабатывающих три копейки преподов (господи, какой там мог быть авторитет для пупа земли?!) были гораздо более умными чем я, думавший, что расставляю приоритеты!

          Вопрос дня — как донести эту мысль до сегодняшнего студента, похожего на меня из прошлого?


          1. Maxim_Andreev
            09.11.2018 23:37
            #19347054
            +1

            За эти семь лет мне успела пригодиться почти каждая из дисциплин, и каждую пришлось заново самостоятельно изучать.

            Присоединяюсь. Тоже во время учёбы смело отметал матан как что-то ненужное, а в итоге просто потратил на его усвоение больше времени уже во время работы.
            Вопрос дня — как донести эту мысль до сегодняшнего студента, похожего на меня из прошлого?

            Думаю, доносить что-то вовсе необязательно. В худшем случае усвоение произойдёт методом последовательных приближений по мере надобности. В лучшем случае человек так ничего и не поймёт, устроится работать по рабочей специальности, будет рассказывать всем, что он разработчик, матан ему вообще ни разу не пригодился и будет при этом абсолютно счастлив и уверен в себе.


            1. ganqqwerty
              10.11.2018 00:56
              #19347240

              Думаю, доносить что-то вовсе необязательно.

              Ну тут у нас с вами целеполагание разное — я все же к коммунистическому идеалу «всестороннего развития всех членов общества» склонен, чтобы каждый ребенок смог раскрыться настолько, насколько возможно.


              1. Maxim_Andreev
                10.11.2018 15:11
                #19348520

                А по-моему, у нас почти одинаковое целеполагание. Нужно дать возможность каждому освоить любую специальность, но заставлять ни к чему. И обманом заманивать тоже никого не нужно. А то люди будут поступать в университет ради непрекращающихся развлечений, а потом в лекционном зале вместо клоуна с медведями столкнутся с предельно абстрактными задачами и формулами.
                Для мотивации я бы добавил разве, что крепкая математическая подготовка — это то, за что очень ценят специалистов из бСССР на Западе (где как раз распространена манера преподавать матан любой сложности посредством шоу и примитивных шуточных задачек).


            1. saboteur_kiev
              10.11.2018 02:06
              #19347330

              А никто и не утверждал, что матан и другие дисциплины не нужны.

              В статье говорится, что при обучении преподы, учебники, и многие доступные материалы (википедия), приводит объяснения без привязки к реальным практическим задачам.
              Слишком часто объяснения идут излишне формальным языком, который перегружен другими формальными определениями.

              Возможно в энциклопедиях и справочниках для продвинутых математиков и полезно использовать полный формализм, чтобы учесть все нюансы, но не в общедоступных википедии и школьных учебниках.

              Особенно часто встречаются резкие переходы типа «берем один апельсин и одно яблоко, как вы видите все несложно, теперь очевидно что из этого получается )@K$&%H@#JK$H#@$*@#%$HJ@#%(@#JK» выглядит как-то так.


              1. Maxim_Andreev
                10.11.2018 15:23
                #19348550

                Я тоже не утверждал, что кто-то утверждал) Просто ответил на комментарий выше.
                По поводу школьников, я вообще не понимаю, зачем им нужен матан. Детей как раз важно просто заинтересовать какой-то специальностью. Даже в случае с техническими специальностями, на мой взгляд, для этой цели больше подходит обществознание, чем математика или физика. А уж как запускать ракеты посредством матана их научат уже в ВУЗах.
                А Википедию вообще можно править самостоятельно, насколько я понимаю.

                По поводу практических примеров, я тоже очень этого хотел на младших курсах. Но сейчас я понимаю, что если бы вместо абстрактных задачек мне на 2-м, 3-м курсе стали бы объяснять как рассчитать при помощи комплексных чисел гидравлический четвертьволновой газитель пульсаций, я бы точно психанул или ушёл в глубокую депрессию.


      1. AAngstrom
        09.11.2018 22:49
        #19346912

        Доверие, безусловно нужно, иначе вообще непонятно, зачем идти в универ. Но честно говоря, не очень понятно, какое это отношение имеет к проблеме качества университетского образования. Университетские программы составляются в расчёте на определённую специальность. Например, специальность прикладная математика будет подразумевать, сюрприз, много разной математики.

        Не знаю, кого Вы подразумеваете под «программистом». Сейчас это понятие размылось настолько, что это может означать и как человека, разрабатывающего с нуля ОС реального времени для новой архитектуры, так и мальчика, меняющего катриджи в принтерах. Если смотреть в официальные документы, то есть специальность 09.02.03 «Программирование в компьютерных системах». Она относится к среднему профобразованию, по ней готовят 2 года в ПТУ (или, как они сейчас себя называют, в «коллЕджах»). Там, действительно, вряд ли нужно интегральное исчисление, но его там вряд ли и преподают.

        С другой стороны, то, что в России компании от любого эникейщика ожидают чуть ли не кандидатской степени, относится к ещё одной проблеме, связанной с девальвацией высшего образования как такового. «Если уж у нас даже уборщица факультет машиностроения с красным дипломом закончила, то Вы, товарищ системный администратор, не можете у нас со своим среднеспециальным дипломом работать.»

        Но всё это — совершенно другая тема, и к делу преподавания математики никак не относится.


        1. ganqqwerty
          09.11.2018 23:26
          #19347020

          Вы просто отмахнулись от проблемы доверия. А я думаю, что доверия к институтам, во-первых, сегодня крайне мало, во-вторых, его отсутствие вызвано объективными социоэкономическими причинами, в-третьих, оно подрывает образование и самообразование со страшной силой.


  1. fierce-katie
    09.11.2018 09:40
    #19343316
    +6

    Получив профильное образование, вспоминая свои лекции на первых курсах, заметила, что у многих преподавателей как будто психологический барьер: категорически не хотят объяснять на пальцах. Как будто студенты подумают, что перед ними не очень продвинутый математик или это как-то ещё погубит их самооценку. Классический сценарий повествования на лекциях: сразу вводятся определения, появляющиеся из неоткуда, потом формулируется теорема с огромным количеством ограничений, а доказательство пишется исключительно языком формул, с минимумом рисунков и пояснений. И ни в коем случае нельзя упустить ни одну мелочь, даже если в прикладных задачах все замысловатые условия теоремы выполняются всегда. Обычно это дословно (точнее, доформульно или даже досимвольно) повторяет учебник. Но, пожалуй, больше всего мне не хватало примеров прикладных задач или хотя бы областей.

    И только лектор по матанализу на первом курсе (что было очень к стати) сначала рассказывал доказательства очень неформально, «размахивая руками», как говорится. И когда уже основные шаги в общих чертах были понятны, формализовал всё сказанное, делая акцент на том, где какое ограничение из условий используется, можно ли без него обойтись и в каких случаях.

    На лекциях по линейной алгебре и теорверу творился мрак: ни одного слова на доске, чистое повторение формул без дополнительных объяснений. Ну нельзя так читать первокурсникам! А потом на старших курсах часто звучала фраза «это должно быть вам известно из курса линейной алгебры», а ты сидишь и смутно вспоминаешь, что такие слова где-то слышал, но сути объекта не понимаешь. Пробелы пришлось самостоятельно восполнять, используя альтернативные ресурсы.

    При этом я не уверена, что неформальным объяснениям место в учебниках. Конечно, там должны быть примеры, чем больше, тем лучше, но степень формальности должна оставаться высокой. Идеально было бы, если бы на лекциях рассказывали всё неформально и на пальцах, больше уделяя внимание вопросам «откуда это взялось, зачем нужно и где используется?». А за формальной записью того же самого уже нужно лезть в учебник, и после человеческих объяснений оно воспримется куда лучше. Но это тоже субъективное мнение, основанное на собственных ощущениях. Конечно, классические учебники не должны быть единственной литературой по предмету. Книжки «для чайников» пригодятся и тем же студентам, которые пропустили объяснения на лекциях, и желающим освоить предмет самостоятельно вне ВУЗа.

    Дополнительные проблемы возникают, когда учебников несколько, и все авторы читают лекции по предмету по-своему. Отличия могут быть минимальны: один в определении пишет знак «больше», а другой — «больше или равно», или изложение идёт в разном порядке. Из-за этого разгорается методическая гражданская война. А потом на экзамене только попробуй сказать определение из учебника профессора Х, отвечая билет профессору У.

    Сначала думала, что пост будет про нотацию математических выражений. Там хоть и есть свои сложности, без неё было бы гораздо хуже :)


  1. dmagin
    09.11.2018 09:43
    #19343322

    Перед математиками стоят такие же проблемы, как и перед программистами.
    Три основных проблемы — и все сложные.
    1. Разобраться в какой-либо области (вопросе, проблеме).
    2. Зафиксировать понимание, описав эту область (вопрос, проблему) так, чтоб тебя поняли другие.
    3. Реализовать область (вопрос, проблему) в виде набора инструментов (программ), чтобы можно было «руками пощупать».


  1. dim2r
    09.11.2018 09:49
    #19343342
    +1

    Встречался с таким заблуждением — сначала будем строить простую модель, потом будем дополнять её деталями и все больше приближаться к реальности. В реальности, так можно делать с линейными зависимостями. Когда есть нелинейные зависимости, то простое добавление деталей приводит к тому, что модель сильно уходит в сторону от реальности.

    Когда моделировал поведение плазмы встречался с таким. Добавляешь в программу обработку еще одного физического эффекта и модель просто рушится и программа производит какую-то ерунду. Поэтому простые модели рулят, а добавление параметров и адаптация к реальности — это особое искусство.


  1. martin_wanderer
    09.11.2018 11:10
    #19343618
    +2

    Спасибо за длину кривой. Это прекрасно!


    1. Akon32
      09.11.2018 22:13
      #19346800
      +1

      Если спустя n лет после выпуска пролистать учебник по матану, можно найти много прекрасного, особенно если не нужно готовиться к экзаменам. Во всяком случае, мне показалось так.


    1. akhalat
      10.11.2018 06:00
      #19347520

      картинка хорошая, но она есть, пожалуй, в каждом первом учебнике, в том числе, конечно, и в Фихтенгольце:


  1. mikhailian
    09.11.2018 11:28
    #19343718

    А мне вот нравятся книги Халида Азад по математике. Иррациональные числа он очень легко объясняет через геометрические примеры в Math, Better Explained.


  1. Stormwalker
    09.11.2018 11:46
    #19343824
    +1

    Раз уж зашла речь о математике в массы — порекомендую всем серию лекций Алексея Савватеева — математика для гуманитариев. Человек на пальцах объясняет важные математические понятия, приводит конкретные примеры, и учит людей думать. Он преподает математику в школах, но не уверен, воспримут ли таких людей в обычной школе.
    На первом занятии, например, на пальцах доказал, что невозможно собрать пятнашки, если поменять местами 14 и 15.


    1. Eugney
      09.11.2018 18:49
      #19346084

      У Владимира Итенберга хорошие беседы о математике, для начинающих самое то.


    1. Ingref
      10.11.2018 17:57
      #19348976

      Кстати, по этим лекциям Савватеев выпустил книгу. Так вот — она абсолютно нечитаемая! Если сравнивать книгу и сами лекции (видео) — это день и ночь в плане понятности. Это я к тому, что писать «учебники» действительно надо уметь, и это не зависит от умения объяснять…


  1. speshuric
    09.11.2018 11:53
    #19343870

    Дубль


    1. Oxoron Автор
      09.11.2018 12:10
      #19343956

      При подсчете на бумажке слишком много внимания\времени уходит непосредственно на вычисления. Даже если берутся малые числа вроде (13, 19).

      Плюс, если кто-то считает на доске — часть внимания слушателей уходит на проверку арифметики. Если же аудитория считает раздельно: кто-то заканчивает сильно быстрее, а кто-то сильно медленнее, и разброс достаточно серьезен.

      С другой стороны, при самообучении таких проблем не возникает, так ручной счет может быть актуальным.


  1. speshuric
    09.11.2018 11:55
    #19343886

    Так, примеры «на бумажке» никак не помогают осознать RSA
    Вот как раз наоборот. RSA идеален для обьяснения на пальцах, а замороченные поточные типа AES — нет, хотя в AES идеи более интуитивное и менее "математичные"


    1. mikhailian
      09.11.2018 12:03
      #19343934

      Diffie-Hellman легко объяснить на пальцах, RSA уже сложнее.


  1. ankh1989
    09.11.2018 12:06
    #19343942

    Мне эта статья напомнила картинку с какими то американскими тестами где всё предельно практично: на счету 100 денег, процент в банке такой то, сколько будет через 5 лет. Вообще если вам нужны такие кондовые примеры для понимания картины и если определение предела вызывает у вас трудности, то математика не для вас и в этом нет ничего плохого: кто то не видит смысла общаться с людьми, а кого то от этого прёт. Как только вступление с определением предела пройдёт и начнётся настоящая математика с псевдогильбертовыми бесконечномерными компактными подмножествами конечномерных многообразий, примеры из реальной жизни не помогут. математикой занимаются как мне кажется ради достижения такого состояния «ощущения полноты картины» — кто то курит косят ради особых ощущений, монах медитирует свою медитацию для такого ощущения, а математик дотошно разбирается в особо абстрактной и такой же бесполезной теореме и тащится от ощущения понимания всей картины. Проблема математики вовсе не в том, что её мало кто может осилить, а в том язык математики застрял в эпохе античности: одни почтенные старцы пишут доказательство теоремы руками на пергаменте, а другие не менее почтенные старцы потом это 10 лет проверяют.


  1. Whuthering
    09.11.2018 12:07
    #19343944
    +4

    чуть менее популярные ребята даже запилили инструкцию «Как читать математику».

    Там, кстати, с самого начала прекрасный пример, иллюстрирующий этот пост:

    «Когда вы складываете последовательные числа, начиная с 1, и количество слагаемых нечётное, то результат равен произведению среднего числа на последнее. Для современной математики естественно будет записать теорему следующим образом:
    image
    Читателю понадобится примерно столько же времени, чтобы распутать эту небольшую формулу, сколько ему нужно на понимание двух строчек текстовой версии теоремы. Пример теоремы Леви:
    image    »


  1. poxvuibr
    09.11.2018 12:42
    #19344134
    -2

    Вот этот пример с баром, Анжелиной Джоли и девушками очень жизненный и понятный, да. Вообще математики это такие люди, которые известны своей способностью зажигать в барах и отрываться на вечеринках а также клеить моделей. Да что там математикам, вообще большинству молодёжи это близко и знакомо.


    В отличие от примеров, допустим, с компьютерными играми, где у танка есть какая-то вероятность пробить броню другого танка, зависящая от многих параметров. Ну, или в Старкрафте где так-то тоже есть что поанализировать или там ещё огромная куча MMO, где надо уметь собрать экипировнку и команду. Это всё, конечно, не очень примеры, они молодёжи не близки.


    1. BugM
      09.11.2018 13:16
      #19344322

      Есть HS с его случайными целями и случайными заклинаниями.
      2 простых параметра и готовы близкие студентам примеры на любые случаи теории.


  1. TimsTims
    09.11.2018 13:01
    #19344250
    +2

    Да что там ВУЗ! Вы давно открывали школьный учебник? Вспоминаю, как у сестры началось деление. Так там сразу с порога что-то вроде: «частное это результат деления делимого на делитель». И всё. Только цитата была посложнее, на уровне очень правильной формальной математики учитывающей деление на 0. И разбирайся дальше как хочешь, решай задачи. Честно говоря я сам сразу с порога не понял, и был просто в шоке, что так сложно объясняется деление…

    Вместо того, чтобы просто написать что-то вроде этого:

    Сколько раз 3 содержится в 14?
    Повторяя операцию вычитания 3 из 14, мы находим, что 3 содержится в 14 четыре раза, и ещё «остаётся» число 2.


    1. Druu
      09.11.2018 15:36
      #19345070
      +4

      Вспоминаю, как у сестры началось деление. Так там сразу с порога что-то вроде: «частное это результат деления делимого на делитель»

      Действительно, следовало написать: "деление — это умножение на обратный элемент". И про ноль тогда ничего пояснять не надо — для нуля обратного нет.


  1. Newm
    09.11.2018 13:04
    #19344266
    +1

    Полагаю, что в соответствии с научным подходом автору было бы не плохо ознакомиться с предшественниками, которые критиковали современные подходы к преподаванию математики. Начать можно с www.google.ru/search?newwindow=1&ei=u1DlW-zwB8SOmgXq-YuADA&q=%D0%B0%D1%80%D0%BD%D0%BE%D0%BB%D1%8C%D0%B4+%D0%BE+%D0%BF%D1%80%D0%B5%D0%BF%D0%BE%D0%B4%D0%B0%D0%B2%D0%B0%D0%BD%D0%B8%D0%B8+%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8&oq=%D0%B0%D1%80%D0%BD%D0%BE%D0%BB%D1%8C%D0%B4+%D0%BF%D1%80%D0%B5%D0%BF%D0%BE%D0%B4%D0%B0%D0%B2%D0%B0&gs_l=psy-ab.3.0.0i22i30k1.48957.53779.0.55124.17.16.0.1.1.0.70.973.16.16.0....0...1c.1.64.psy-ab..0.17.976...0j0i131k1j0i67k1j0i10i67k1.0.MOcRmurZlw4

    В свое время я офигел от учебника 50-х годов по уравнениям в частных производных, который читался почти как художественная литература. Там было ВСЕ понятно. На фоне всех остальных учебников он смотрелся дико:).


    1. Oxoron Автор
      09.11.2018 13:18
      #19344336

      Если я не указал список литературы, это еще не значит, что я не читал Арнольда. Предлагаю обмен: я вам ссылку на Фейнмана (читайте про образование в Бразилии, поиск по "Что касается образования в Бразилии, то у меня был очень интересный опыт."), в вы ссылку на УрЧаПы. Тогда у нас будет по две ссылки.


      1. Newm
        09.11.2018 14:32
        #19344716

        В сети не могу найти. По моим воспоминаниям (25+ лет уже прошло) это была книжка Петровский И.Г. «Уравнения в частных производных» (возможно дифференциальные). Точно помню, что за нее дана Сталинская премия, о чем было в ней упоминание. Умопомрачительная полиграфия. За 40 лет, сколько было на момент моего знакомства с этой книжкой, она практически не истрепалась.


        1. zartarn
          10.11.2018 00:15
          #19347168

          Может вы про

          Заголовок спойлера
          этот
          ссылка намек где искать
          или этот
          image


  1. amarao
    09.11.2018 13:55
    #19344520
    +6

    Я про математику могу сказать одно — 1Blue3Brown.

    www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw

    Более зажигающего видео про линейную алгебру (и матанализ) я не видел.


    1. fierce-katie
      09.11.2018 14:33
      #19344718
      +2

      Могла бы плюсануть, обязательно бы это сделала! Только они «3Blue1Brown», но не суть. По линейной алгебре из видео поняла больше, чем после годового курса в университете. Тоже кидала этот канал в комменты к недавнему посту с советами первокурсникам. ИМХО, вот примерно так и нужно рассказывать на лекциях.


    1. Keyten
      09.11.2018 20:31
      #19346436

      Добавлю Welch Labs.
      youtu.be/T647CGsuOVU?list=PLiaHhY2iBX9g6KIvZ_703G3KJXapKkNaF

      За весь ТФКП нам не рассказывали, что график f(x) = x^2 + 1 можно нарисовать так (заодно и видно, что i это корень уравнения x^2 + 1).


      1. ganqqwerty
        09.11.2018 23:29
        #19347030
        +1

        Мне не видно. Где это видно? Почему график объемный? Что означает цветовое кодирование? Что у нас по оси z вообще? Почему все перевернуто? Помогите, я хочу проникнуться прекрасностью этого примера.


        1. akhalat
          10.11.2018 06:43
          #19347556

          заодно и видно, что i это корень уравнения x^2 + 1

          вся шутка в том, что на самом деле на картинке этого НЕ видно, т.к. пересечение поверхности с плоскостью $z=0$ даёт кривую $y^2-x^2=1$, содержащую бесконечно много точек вида $(x,\pm\sqrt{1+x^2})$. чтобы найти на этой кривой точки, которые будут соответствовать решению исходного уравнения, надо дополнительно учитывать условие $xy=0$, получаемое из равенства для мнимой части


  1. SomaTayron
    09.11.2018 14:09
    #19344596
    +2

    Примеры хорошие, но по сути это приводится именно рафинированный прикладной подход, а не фундаментальный. Не скажу, что такая система плоха, но она просто иная — ей мы готовим инженера, но не готовим ученого, даже выжигаем зачатки склонности. Это аналог тестовых ЕГЭ по литературе — проверить, что человек читал материал, это поможет, но не покажет, анализировал ли он его. В идеале конечно хорошо бы знать возможности ребенка и при отсутствии склонности к умозрительному подходу обучать чисто эмпирически, но это только мечта. Поэтому в советской школе давали всем фундаментальных вариант (насколько хороша давали — это уже другой вопрос), а далее или переобучали на прикладника или уже развитие продолжалось в университете. В западной же системе почти всем дают прикладную бузу, а элиту сразу учат по фундаментальной методике.

    Кстати, слова Евклида можно трактовать по-разному. Александрийская школа объединяла вавилонскую (после аккадского завоевания) и египетскую систему счета, поэтому совмещала полупозиционное счисление в совокупности с рядами. В итоге часть расчетов велось пропорциями (фактическая тригонометрия), а часть — взаимными переводами между рядами и системой вавилонских дробей (дробь первого порядка со знаменателем 60, второго — со знаменателем 602).
    Для текста, формул и чисел использовались одни и те же буквы (тогда еще 29 было символов — первыми 9 буквами алфавита греки обозначали первые девять чисел; вторые девять букв обозначали первые девяти целым кратным числа десять; и последние девять символов — первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 те же первые 9 букв снабжались штрихами слева).
    Так что говоря о царской дороге он все де подразумевал систему обозначений чисел, отличную от букв, но не связанную с аттической фигурной записью, без этого действительно в научных текстах разобраться было довольно сложно


    1. darthslider
      09.11.2018 16:12
      #19345254

      А насколько передовая теоретическая математика сейчас оторвана хоть от каких-то прикладных областей?
      Я к тому, что даже самые передовые вещи же наверное доказывают не «потому что мы смогли», а еще и потому что это как-то можно будет использовать в вычислениях чего-то прикладного?


      1. SomaTayron
        09.11.2018 17:46
        #19345780

        по правде говоря — когда как.
        Кеплер ведь изначально строил модель солнечной системы по принципу вложения правильных многоугольников. Теория не подтвердилась, но сейчас об этом мало кто помнит. Однако тот же Субботин реинкарнировал эту теорию немного с другой стороны, приняв, что система является соединением 2 систем — классической (от Юпитера) и аномальной (до Земли). И теория видимо достаточно близка к истине. Хотя есть и неприятный момент — приход в равновесие (согласование) этих систем станет концом нашей солнечной системы.
        За базу взята реальная модель, но абсолютно оторванная от практической применимости- тут скорее спортивный интерес )


      1. Druu
        09.11.2018 22:05
        #19346766

        Я к тому, что даже самые передовые вещи же наверное доказывают не «потому что мы смогли», а еще и потому что это как-то можно будет использовать в вычислениях чего-то прикладного?

        Именно "потому что мы смогли", математикой ведь занимаются по фану, а не ради какой-то пользы. Естественно, есть исключения.


  1. nmrulin
    09.11.2018 15:38
    #19345086
    +2

    «Я просто читал теорему, выделял главное, писал/решал тривиальные примеры, потом разбирался с формализмом — и реально понимал, о чем идет речь. » -кстати да, сам так делал.
    А учебники действительно так себе. Ради 1% случае, запудривают объяснение так, чтобы никому не было понятно. Зато да, математические выверено.


    1. GeMir
      09.11.2018 17:58
      #19345848

      кстати да, сам так делал
      Открою вам «страшную» тайну: все так делают. Потому что так и задумывалось :)
      А учебники действительно так себе.
      То, что вам попадались не лучшие (для вас) учебники, говорит скорее о неудачном выборе литературы (а её много разной, не стоит останавливаться на одном учебнике даже самого популярного автора).

      Математическая нотация создана с целью достижения максимально однозначной «читаемости», а не для того, чтобы её можно было как художественную литературу или музыку читать и понимать «с листа».


  1. darthslider
    09.11.2018 16:09
    #19345236
    +2

    У меня схожие проблемы были с русским языком в школе.
    Тебе просто говорят «жи/ши пиши через и» и всё. Просто набор догм.
    А потом я почитал, например, «Слово о словах» и узнал, что у всех правил есть история и какие-то причины и стало как-то гораздо интереснее.

    Сейчас сам немного преподаю и всегда при подготовке материала готовлюсь ответить на вопросы вида «а нафига это вообще?» и, что немаловажно, регулярно этот вопрос задают. И вижу у студентов интерес к предмету, что чертовски приятно.


    1. Zenitchik
      09.11.2018 16:30
      #19345378

      Русский язык в школе — это технология. Там нет причин. Вернее, есть, но они исторические, а не рациональные.


      1. darthslider
        09.11.2018 16:35
        #19345414

        Но даже с историческими причинами гораздо интереснее. Не потому что так сказал учитель, а потому что так сложилось исторически, вот занимательная история и примеры.


  1. FlameArt
    09.11.2018 17:34
    #19345714

    Как можно улучшить подачу материала в математических текстах

    В текущих (российских) реалиях — никак. Энтузиасты есть, профессионалы есть, мотивации нет.


    Надо просто поднимать время от времени хайп по поводу того, что математик — уважаемый человек, аналогично и к учёному. Когда учёные поймут, что их могут полюбить массы за то, что те доступным языком описали какие-то сложные вещи, или даже выложили такое описание на ютуб, мотивация сразу появится, я гарантирую.

    Но пока у нас прививается только любовь к западным учёным, к западным космическим агенствам, а любые отечественные начинания несправедливо охаяны и высмеяны с ног до головы, мало какому учёному или профессору захочется после этого ради этих людей что-то нормальное писать. И поделом. Так что сам факт этой статьи — это уже хайп в правильном направлении, надо просто немного оптимизма и уважения добавить.


  1. GeMir
    09.11.2018 17:42
    #19345758

    Помните школу? А формулу дискриминанта? А как она доказывается/выводится?
    Дискриминант в школах Германии не в ходу. Школьники знают «pq-формулу», которая подходит для решения приведённых квадратных уравнений. Выводится при помощи дополнения квадрата, формул сокращённого умножения и эквивалентных преобразований.
    …
    image


  1. ganqqwerty
    09.11.2018 18:03
    #19345878
    +1

    Я вот еще один аспект затрону — слабая техническая составляющая современных учебников. Большинство электронных учебников 21-го века ничем не отличаются от таковых 17-го века. Почему я не могу кликнуть по абсолютно каждому слову во фразе или по буковке в формуле и хотя бы перейти по гиперссылке или увидеть попап с кратким пояснением того? Особенно для тех разделов математики, где у нас вводится очень много определений, понятий и дополнительных буковок.

    В итоге читаешь-читаешь книжку — и внезапно появляется перевернутый треугольничек, с двумя индексом — и ты начинаешь листать и листать книжку назад, находишь, где автор ввел треугольничек, через пять страниц — где он записал эти индексы. А проблема простая, на написание электрических учебников у нас распиливается невероятное количество денег, мааленькую порцию которых можно было бы выделить на то, чтобы скажем html-изировать Фихтенгольца.


    1. khim
      09.11.2018 18:36
      #19346026
      +2

      Это вообще совсем отдельная история. И в США и в России и, похоже, во всём мире выпуск учебников — это очень доходный бизнес. Которому не нужны хорошие учебники. Ему нужны новые учебники!

      Помните у Фейнмана?

      Очередь дошла до книги, которая была частью трехтомного сборника, выпускаемого одним издательством, и меня спросили, что я о ней думаю.
      Я сказал: «Эту книгу мне не прислали со склада, но две другие были хорошие».
      Кто-то попытался повторить вопрос «Что Вы думаете об этой книге?». — Я уже сказал, что мне ее не прислали. Так что я не могу о ней судить. Работник книжного склада был здесь же и сказал: «Извините, я могу все объяснить. Я не прислал Вам эту книгу, так как она не была еще закончена. По правилам мы должны иметь каждую книгу к определенному сроку, а издатель задержался с ней на несколько дней. Поэтому нам прислали макет книги с обложкой и пустыми страницами внутри. Компания приносит свои извинения и надеется, что трехтомник будет обсужден, несмотря на задержку третьего тома».
      Оказалось, что этот пустой макет был оценен некоторыми членами комиссии! Они не могли поверить, что книги не было, ведь оценки-то были. Более того, оценки у несуществующей книжки были выше, чем у двух других. То обстоятельство, что книги не было, ничуть не помешало ее оценке.
      Это, правда, по подходам в США — но я сильно что-то сомневаюсь, что в России ситуация сильно лучше.


      1. ganqqwerty
        10.11.2018 01:07
        #19347268

        ну блин, неужели нигде ничего нет? Нормальный гипертекстовый calculus или там алгебра.


        1. zartarn
          10.11.2018 01:23
          #19347284

          Некоторые учебные заведения делают для внутреннего пользования учебники на SunRav. Там и гиперссылки, и видео, и тесты, и чего только нет. Всё на что хватит фантазии того кто делает. Но все равно это уровня методичек, а не полноценных учебников.


  1. WinPooh73
    09.11.2018 18:49
    #19346082

    «Я могу научить дифференцировать любого. Дайте только розгу. Дайте розгу, и вот этот… нет, лучше — этот, будет дифференцировать. Дайте только розгу. И свяжите ему руки. А потом руки развяжут, и он будет дифференцировать.»
    © И.А.Борачинский, МФТИ


    1. ganqqwerty
      09.11.2018 19:32
      #19346232

      наш препод говорил, что научить дифференцировать можно даже козу. А вот интегрировать козу научить нельзя.


      1. GeMir
        10.11.2018 00:42
        #19347206
        +3

        научить дифференцировать можно даже козу
        Дифференцирование — это как выдавить зубную пасту из тюбика. Интегрирование — попытка вернуть оную обратно в тюбик :)


  1. Keyten
    09.11.2018 20:25
    #19346418
    +1

    Очень крутая статья.

    Вспомнился мой матан первого курса. Предел по эпсилон-дельта. Никто не понимал, все просто зубрили, и всё. Я сам несколько дней (то ли в ноябре, то ли уже в декабре) ходил и думал, и в какой-то миг внезапное озарение: а давай считать эпсилон каким-то очень маленьким числом! Тогда всё неожиданно встаёт на свои места.
    Потом уже узнал, что похожим подходом (с очень маленькими числами) руководствовались Ньютон и Лейбниц, изобретая анализ, а потом пришёл Коши, наприводил контрпримеров и усложнил, чтоб всё формально и логично.

    Потом уже не так сложно: определение производной (как delta_y / delta_x, delta_x -> 0) быстро понялось само, интеграл Римана интуитивно понятен из гифки в Википедии (благо, аппроксимировать площади я умел ещё в 8 классе как минимум), а через какое-то время ещё и узнал, что ? это просто запись для lim sum(...), а dx для delta_x внутри суммы.

    Пример из статьи с интегралом по контуру я узнал во втором семестре на вариационном исчислении. Очень крутой препод, очень классно рассказывал, походя проливая свет и на другие предметы. Даже жаль, что не хватало знаний, чтобы понимать, о чём он говорит, полностью, хотя логику рассуждений вроде бы прослеживали. Но звучало всё равно как магия. Горестно взмахивал руками, узнавая, что мы не умеем в дифуры и ТФКП, и зачем нам вообще вариационное исчисление и функан на 1 курсе.
    Он же и сказал, что dx это просто очень маленький кусочек x, и по теореме Пифагора получается интеграл по контуру. Тогда не полностью это получилось понять и осознать, и только физика в следующем семестре, где подход типа «порежем тело на маленькие кусочки dx» является совершенно обычным, наконец сделала нас хоть что-то понимать.


    1. Zenitchik
      09.11.2018 21:20
      #19346572

      а давай считать эпсилон каким-то очень маленьким числом

      Эээ… А разве теорема Коши не звучит как "… для сколь угодно малого эпсилон ..."?
      В суть теоремы я тоже тяжело врубался, и врубился только после экзамена (каким чудом я его сдал?..)


  1. Akon32
    09.11.2018 21:34
    #19346634

    Есть разные мнения, чем занимается и чем является математика. Изложу (в вольном виде) немного мыслей из книги "Апология математика" Г. Харди, с которыми, впрочем, я не вполне согласен.


    Есть 2 (как минимум) реальности — наша и математическая. В "нашей" находимся мы, атомы, физические законы — то, чем занимается физика, то, что мы видим и ощущаем. В "математической" находятся абстрактные математические объекты — числа, отношения, структуры и т.д. Когда математик описывает новый объект (например, кватернион, или тензор, или теорему), он не придумывает и не конструирует его, а открывает существующий в математической реальности объект. Настоящая математика — она про изучение другой, математической реальности, а не нашей.
    Иногда случается, что абстрактные математические объекты находят применение в описании нашей реальности. Бывает, что от математика даже требуется, чтобы он описал математические объекты "на заказ", под нужды например физиков. Поэтому другое, более прикладное и "приземлённое" толкование сущности математики — математик конструирует, придумывает математические объекты. Но эта "инженерная" математика (в частности, интегралы), хотя и несёт в себе огромную пользу, не настоящая. Настоящая, абстрактная математика полностью бесполезна.

    Какого толкования придерживаться — вопрос веры. Вот тут и начинаются срачи, нашедшие отражение даже в рассказах WH40k.
    По одну сторону "чистые" математики, которые обитают в своём мире и которым плевать, нужно ли студентам то, что они рассказывают.
    По другую — студенты, школьники, которые пытаются понять то, что рассказывают математики, но за неимением практического применения абстрактных вещей рассказанное понять не могут. Потом они говорят "Зачем мне в жизни синусы?" и "Я на следующий день после экзамена всё забыл, и за 20 лет ничего не пригодилось".
    Где-то между полюсами находятся инженеры (+ экономисты и прочие), которые поняли матан и имеют с этого наибольший профит; и прикладные математики, которые объяснили инженерам.


    Основная проблема обучения (инженеров) математике в том, что проще и эффективнее обучать их именно абстрактным вещам — это даёт им возможность гибко применять абстрактные вещи, если сами осилят найти применение. Другой полюс — обучение чисто на примерах, без теории, показал свою неэффективность где-то пару веков назад.
    Но учить абстрактные вещи сложно и часто ненужно, поэтому соблюдают некоторый баланс между абстрактной математикой и прикладной, например дают абстрактное определение матрицы и определителя матрицы, а о применениях студенты узнают сильно позже (совсем же абстрактные вещи инженерам вовсе не дают). Вот в эти моменты и бывает непонятно, зачем нужна математика и почему её объясняют так ненаглядно. Конечно, хороший преподаватель и/или хорошая программа обучения могут сгладить эти моменты, но так бывает не всегда.
    Вот и получается, что учат абстрактным вещам, не говоря заранее о применениях. И это как-то работает.


  1. McAaron
    09.11.2018 21:42
    #19346660
    -5

    Если тебе не понятно, иди гоняй танчики или еще какие безделицы.


  1. mikeus
    09.11.2018 23:53
    #19347106
    +1

    Если говорить о преподавании математики, то характер проблемы на мой взгляд точно сформулировал в своё время (1981) В.А.Рохлин:

    В наше время можно окончить среднюю школу и не решить, в действительности, ни одной математической задачи. Даются шаблоны, примеры, подражая которым дети и справляются со своими школьными обязанностями.
    Я бы то же самое добавил и про физику. И собственно, тем же макаром большинство успешно продолжают учиться в институтах. (И мне вспоминаются ещё слова В.И. Арнольда о том, что математика — это та часть физики, в которой эксперименты дёшевы.)


  1. F376
    10.11.2018 09:32
    #19347710

    Автору, да и всем очень рекомендую прочесть книгу
    М.Клайн «Математика Утрата определенности» Москва «Мир» 1984