На данный момент я предполагаю разбить текст на три статьи:
- 1. Ликбез по теории вероятностей и как она связана с методами наименьших квадратов
- 2. Наименьшие квадраты, простейший случай, и как их программировать
- 3. Нелинейные задачи
Я зайду к наименьшим квадратам чуть сбоку, через принцип максимума правдоподобия, а он требует минимального ориентирования в теории вероятностей. Данный текст рассчитан на третий курс нашего факультета геологии, что означает, (с точки зрения задействованного матаппарата!) что заинтересованный старшеклассник при соответствующем усердии должен суметь в нём разобраться.
Насколько обоснован теорвер или верите ли вы в теорию эволюции?
Однажды мне задали вопрос, верю ли я в теорию эволюции. Прямо сейчас сделайте паузу, подумайте, как вы на него ответите.

Лично я, опешив, ответил, что нахожу её правдоподобной, и что вопрос веры тут вообще не встаёт. Научная теория имеет мало общего с верой. Если кратко, то теория лишь строит модель окружающего нас мира, нет необходимости в неё верить. Более того, критерий Поппера требует от научной теории иметь возможность опровержения. А ещё состоятельная теория должна обладать, в первую очередь, предсказательной силой. Например, если вы генетически модифицируете сельскохозяйственные культуры таким образом, что они сами будут производить пестициды, то вполне логично, что будут появляться устойчивые к ним насекомые. Однако существенно менее очевидно, что этот процесс может быть замедлен благодаря выращиванию обычных растений бок о бок с генномодифицированными. Основываясь на теории эволюции, соответствующее моделирование сделало такой прогноз, и он, похоже, подтвердился.
А при чём тут наименьшие квадраты?
Как я упомянул ранее, я зайду к наименьшим квадратам через принцип максимального правдоподобия. Давайте проиллюстрируем на примере. Предположим, что нам интересны данные о росте пингвинов, но мы можем измерить лишь несколько этих прекрасных птиц. Вполне логично ввести в задачу модель распределения роста — чаще всего она нормальная. Нормальное распределение характеризуется двумя параметрами — средним значением и среднеквадратичным отклонением. Для каждого фиксированного значения параметров мы можем посчитать вероятность того, что будут сгенерированы именно те измерения, что мы произвели. Дальше, варьируя параметры, найдём те, что максимизируют вероятность.
Таким образом, для работы с максимальным правдоподобием нам нужно оперировать в понятиях теории вероятностей. Чуть ниже мы «на пальцах» определим понятие вероятности и правдоподобия, но сначала я хотел бы заострить внимание на другом аспекте. Я на удивление редко вижу людей, которые задумываются над словом «теория» в словосочетании «теория вероятностей».
Что изучает теорвер?
По поводу того, каковы истоки, значения и область применимости вероятностных оценок, уже не первую сотню лет идут яростные споры. Например, Брюно Де Финетти заявил, что вероятность есть не что иное, как субъективный анализ вероятности того, что что-то произойдёт, и что эта вероятность не существует вне ума. Это готовность человека делать ставки на что-то происходящее. Это мнение прямо противоположно взгляду классиков / фреквентистов на вероятность конкретного результата события, в котором предполагается, что одно и то же событие может повторяться многократно, а «вероятность» конкретного результата связана с частотой выпадения конкретного результата во время повторных испытаний. Помимо субъективистов и фреквентистов есть ещё и объективисты, утверждающие, что вероятности — это реальные аспекты универсума, а не просто описания степени уверенности наблюдателя.
Как бы то ни было, но все три научные школы на практике используют один и тот же аппарат, основанный на аксиомах Колмогорова. Давайте приведём косвенный аргумент, с субъективистской точки зрения, в пользу теории вероятностей, построенной на аксиомах Колмогорова. Приведём сами аксиомы чуть позже, а для начала предположим, что у нас есть букмекер, который принимает ставки на следующий чемпионат мира по футболу. Пусть у нас будут два события: a = чемпионом станет команда Уругвая, b = чемпионом станет команда Германии. Букмекер оценивает шансы команды Уругвая победить в 40%, шансы команды Германии в 30%. Очевидно, что и Германия, и Уругвай победить одновременно не могут, поэтому шанс a?b нулевой. Ну и заодно букмекер считает, что вероятность того, что победит либо Уругвай, либо Германия (а не Аргентина или Австралия) составляет 80%. Давайте это запишем в следующем виде:

Если букмекер утверждает, что его степень уверенности в событии а равняется 0.4, то есть, P(a) = 0.4, то игрок может выбрать, будет ли он делать ставку за или против высказывания а, ставя суммы, которые совместимы со степенью уверенности букмекера. Это значит, что игрок может сделать ставку на то, что событие а произойдёт, поставив четыре рубля против шести рублей букмекера. Или же игрок может поставить шесть рублей вместо четырёх рублей букмекера на то, что событие а не произойдёт.
Если степень уверенности букмекера неточно отражает состояние мира, то можно рассчитывать на то, что в долговременной перспективе он будет проигрывать деньги игрокам, чьи убеждения более точны. Более того, в данном конкретном примере у игрока есть стратегия, при которой букмекер всегда теряет деньги. Давайте её проиллюстрируем:

Игрок делает три ставки, и какой бы ни был исход чемпионата, он всегда в выигрыше. Обратите внимание, что в рассмотрение суммы выигрыша в принципе не входит то, являются ли Уругвай или Германия фаворитами чемпионата, проигрыш букмекера обеспечен! К этой ситуации привело то, что букмекер не руководствовался азами теории вероятностей, нарушив третью аксиому Колмогорова, давайте приведём их все три:
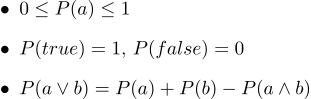
В текстовом виде они выглядят так:
- 1. Все вероятности находятся в пределах от 0 до 1
- 2. Безусловно истинные высказывания имеют вероятность 1, а безусловно ложные вероятность 0.
- 3. Третья аксиома — это аксиома дизъюнкции, её легко интуитивно понять, отметив, что те случаи, когда высказывание a является истинным, вместе с теми случаями, когда b является истинным, безусловно охватывает все те случаи, когда истинно высказывание a?b; но в сумме двух множеств случаев их пересечение встречается дважды, поэтому небходимо вычесть P(a?b).
В 1931 году де Финетти доказал очень сильное утверждение:
Если букмекер руководствуется множеством степеней уверенности, которое нарушает аксиомы теории вероятностей, то существует такая комбинация ставок игрока, которая гарантирует проигрыш букмекера (выигрыш игрока) при каждой ставке.
Аксиомы вероятностей могут рассматриваться как ограничивающее множество вероятностных убеждений, которых может придерживаться некоторый агент. Обратите внимание, что из следования букмекера аксиомам Колмогорова не вытекает то, что он будет выигрывать (оставим в стороне вопросы комиссионных), но если им не следовать, то он будет гарантированно проигрывать. Отметим, что в пользу применения вероятностей были выдвинуты и другие аргументы; но именно практический успех систем формирования рассуждений, основанных на теории вероятностей, оказался привлекательным стимулом, вызвавшим пересмотр многих взглядов.
Итак, мы чуть-чуть приоткрыли завесу того, почему теорвер может иметь смысл, но какими именно объектами он манипулирует? Весь теорвер построен лишь на трёх аксиомах; во всех трёх участвует некая магическая функция P. Более того, глядя на эти аксиомы, мне это очень напоминает функцию площади фигуры. Давайте попробуем посмотреть, работает ли площадь для определения вероятности.
Определим слово «событие» как «подмножество единичного квадрата». Определим слово «вероятность события» как «площадь соответствующего подмножества». Грубо говоря, у нас есть большая картонная мишень, и мы, закрыв глаза, в неё стреляем. Шансы того, что пуля попадёт в данное множество, прямо пропорциональны площади множества. Достоверное событие в данном случае — весь квадрат, а заведомо ложное, например, любая точка квадрата. Из нашего определения вероятности следует, что идеально попасть в точку невозможно (наша пуля — это материальная точка). Я очень люблю картинки, и рисую их много, и теорвер не является исключением! Давайте проиллюстрируем все три аксиомы:
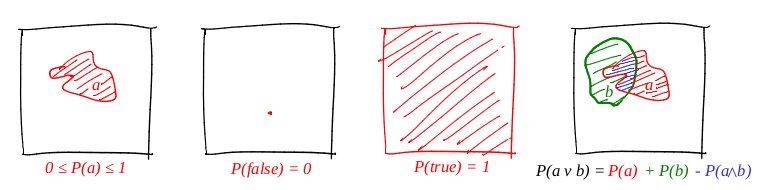
Итак, первая аксиома выполнена: площадь неотрицательна, и не может превысить единицы. Достоверное событие — это весь квадрат, а заведомо ложное — любое множество нулевой площади. И с дизъюнкицей работает отлично!
Максимальное правдоподобие на примерах
Пример первый: подбрасывание монетки
Давайте рассмотрим простейший пример с подбрасыванием монеты, он же схема Бернулли. Проводится n опытов, в каждом из которых может произойти одно из двух событий («успех» или «неудача»), одно с вероятностью p, второе с вероятностью 1-p. Наша задача состоит в том, чтобы найти вероятность получения ровно k успехов в этих n опытах. Эту вероятность нам даёт формула Бернулли:
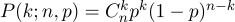
Возьмём обычную монету (p=0.5), подбрасываем её десять раз (n=10), и считаем, сколько раз выпадает решка:
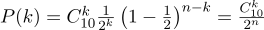
Вот так выглядит график плотности вероятности:
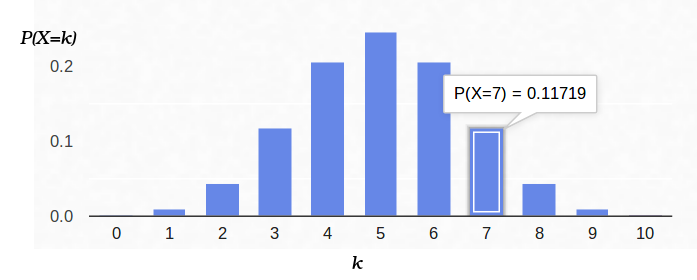
Таким образом, если мы зафиксировали вероятность наступления «успеха» (0.5), и также зафиксировали количество экспериментов (10), то возможное количество «успехов» может быть любым целым числом между 0 и 10, однако эти исходы не являются равновероятными. Вполне очевидно, что получить пять «успехов» гораздо вероятнее, нежели ни одного. Например, вероятность насчитать семь решек составляет примерно 12%.
А теперь давайте посмотрим на эту же задачу с другой стороны. У нас есть реальная монетка, но её распределение априорной вероятности «успех»/«неудача» мы не знаем. Однако мы можем её подкинуть десять раз и посчитать количество «успехов». Например, у нас выпало семь решек. Как нам это поможет оценить p?
Мы можем попробовать зафиксировать в формуле Бернулли n=10 и k=7, оставив p свободным параметром:

Тогда формула Бернулли может быть интерпретирована как правдоподобие оцениваемого параметра, (в данном случае p). Я даже буковку сменил у функции, теперь это L (от англ. likehood). То есть, правдоподобие — это вероятность сгенерировать данные наблюдения (7 решек из 10 опытов) для заданного значения параметра(-ов).
Например, правдоподобие сбалансированной монеты (p=0.5) при условии выпадения семи решек из десяти бросков примерно равняется 12%. Можно построить график функции L:
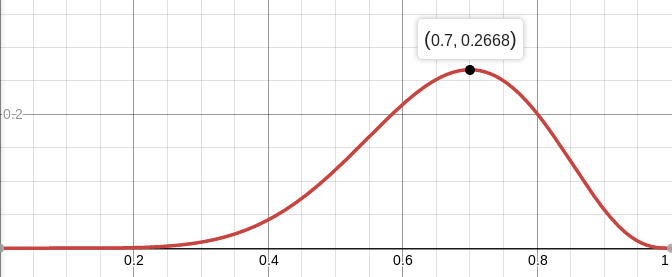
Итак, мы ищем такое значение параметров, которое максимизирует правдоподобие получения тех наблюдений, что у нас есть. В данном конкретном случае у нас функция одной переменной, мы ищем её максимум. Для того, чтобы было проще искать, я буду искать максимум не L, а log L. Логарифм — функция строго монотонная, так что максимизация одного и другого — это строго одно и то же. А логарифм нам разбивает произведение на сумму, которую сильно удобнее дифференцировать. Итак, мы ищем максимум вот этой функции:

Для этого приравняем нулю её производную:
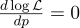
Производная log x = 1/x, получаем:

То есть, максимум правдоподобия (примерно 27%) достигается в точке

На всякий случай посчитаем вторую производную:
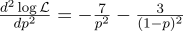
В точке p=0.7 она отрицательна, так что эта точка действительно является максимумом функции L.
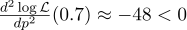
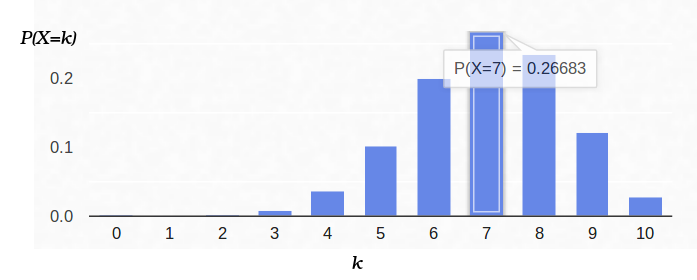
А вот так выглядит плотность вероятности для схемы Бернулли с p = 0.7:
Пример второй: АЦП
Давайте представим, что у нас есть некая постоянная физическая величина, которую мы хотим измерить, будь то длину линейкой или напряжение вольтметром. Любое измерение даёт приближение этой величины, но не саму величину. Методы, которые я тут описываю, разработаны Гауссом в конце 18го века, когда он измерял орбиты небесных тел.
Например, если мы измерим напряжение на батарейке N раз, то получим N разных измерений. Какое из них брать? Все! Итак, пусть у нас будет N величин Uj:
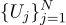
Предположим, что каждое измерение Uj равно идеальной величине, плюс гауссов шум, который характеризуется двумя параметрами — положение гауссова колокола и его «ширина». Вот так выглядит плотность вероятности:
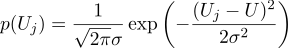
То есть, имея N заданных величин Uj, наша задача найти такой параметр, U который максимизирует значение правдоподобия. Правдоподобие (я сразу беру от него логарифм) можно записать следующим образом:
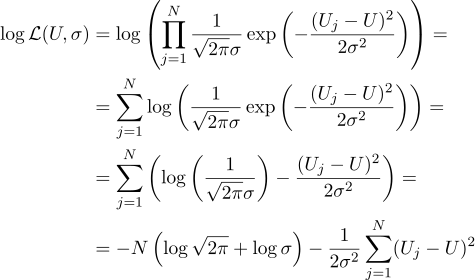
Ну а дальше всё строго как раньше, приравняем нулю частные производные по параметрам, которые мы ищем:
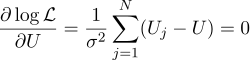
Получим, что наиболее вероятная оценка неизвестной величины U может быть найдена как среднее от всех измерений:
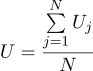
Ну а наиболее вероятный параметр сигма это обычное среднеквадратичное отклонение:
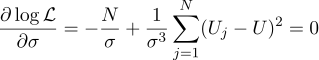

Стоило ли заморачиваться, чтобы получить в ответе простое среднее от всех измерений? На мой вкус, стоило. Кстати, усреднение многократных измерений постоянной величины с целью увеличения точности измерений — это вполне стандартная практика. Например, усреднение АЦП. К слову сказать, для этого гауссовости шума не нужно, достаточно того, что шум несмещённый.
Пример третий, и снова одномерный
Продолжаем разговор, давайте возьмём тот же самый пример, но чуть его усложним. Мы хотим измерить сопротивление некоего резистора. При помощи лабораторного блока питания мы умеем пропустить через него некоторое эталонное количество ампер, и измерить напряжение, которое для этого понадобится. То есть, у нас на вход нашего оценщика сопротивления будет N пар чисел (Ij, Uj).
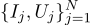
Нарисуем эти точки на графике; закон Ома нам говорит о том, что мы ищем наклон синей прямой.
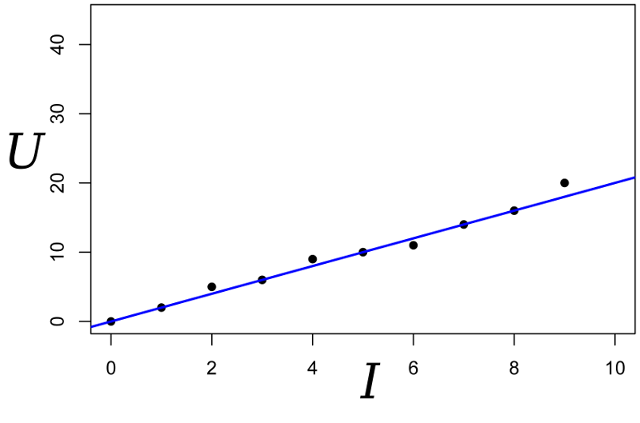
Запишем выражение для правдоподобия параметра R:
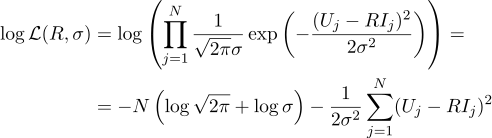
И опять приравняем нулю соответствующую частную производную:
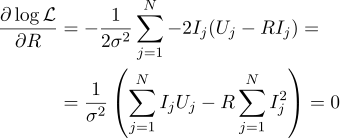
Тогда наиболее правдоподобное сопротивление R может быть найдено по следующей формуле:
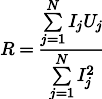
Этот результат уже несколько менее очевидный, нежели простое среднее всех измерений. Обратите внимание, что если мы сделаем сто измерений в районе одного ампера, и одно измерение в районе килоампера, то предыдущие сто измерений практически не повлияют на результат. Давайте запомним этот факт, он нам пригодится в следующей статье.
Четвёртый пример: назад к наименьшим квадратам
Наверняка вы уже обратили внимание, что в последних двух примерах максимизация логарифма правдоподобия эквивалентна минимизации суммы квадратов ошибки оценивания. Давайте рассмотрим ещё один пример. Возьмём калибровку безмена при помощи эталонных грузов. Пусть у нас есть N эталонных грузов массой xj, повесим их на безмен и измерим длину пружины, получим N длин пружины yj:

Закон Гука нам говорит, что растяжение пружины линейно зависит от приложенной силы, а в эту силу у нас входит вес грузов и вес самой пружины. Пусть жёсткость пружины — это параметр a, ну а растяжение пружины под собственным весом — это параметр b. Тогда мы можем вот таким образом записать выражение правдоподобия наших измерений (по-прежнему под гипотезой гауссового шума измерений):
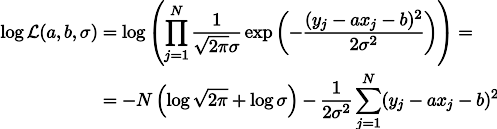
Максимизация правдоподобия L эквивалентна минимизации суммы квадратов ошибок оценивания, то есть, мы можем искать минимум функции S, определённой следующим образом:
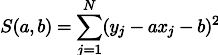
Иными словами, мы ищем такую прямую, которая минимизирует сумму квадратов длин зелёных отрезков:
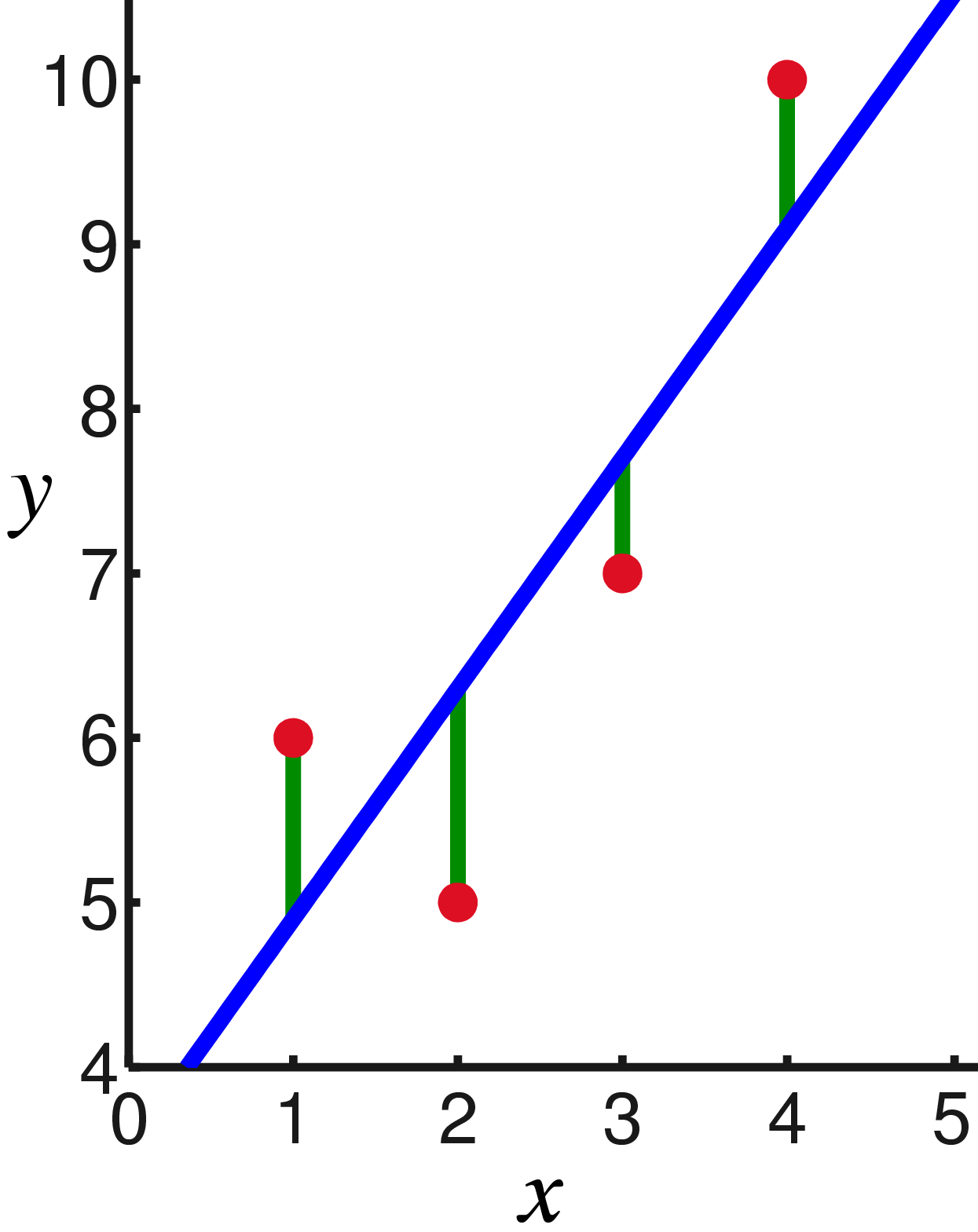
Ну а дальше никаких сюрпризов, приравниваем к нулю частные производные:
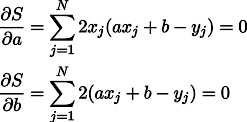
Получаем систему из двух линейных уравнений с двумя неизвестными:
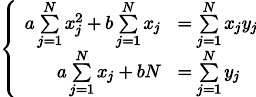
Вспоминаем седьмой класс школы и выписываем решение:

Заключение
Методы наименьших квадратов являются частным случаем максимизации правдоподобия для тех случаев, когда плотность вероятности является гауссовой. В случае же когда плотность (совсем) не гауссова, МНК дают оценку, отличающуюся от оценки MLE (maximum likehood estimation). Кстати, в своё время Гаусс выдвигал гипотезу, что распределение не играет роли, важна только независимость испытаний.
Как видно из этой статьи, чем дальше в лес, тем более громоздкими становятся аналитические решения этой проблемы. Ну да мы не в восемнадцатом веке, у нас есть компьютеры! В следующий раз мы увидим геометрический и, затем, программистский подход к проблеме МНК, оставайтесь на линии.
Комментарии (18)

mao_zvezdun
13.11.2018 11:55+2Про монетку и семь решек (или орлов) я однажды услышал другую задачку, которую потом сам распробовал «на пальцах». Проводился следующий эксперимент — две группы студентов посадили в разные аудитории и первую попросили подбросить сто раз монетку, записав последовательность результатов. А вторую попросили, не подбрасывая, придумать случайную последовательность из ста орлов и решек. Ведущий, посмотрев на результаты, определил где монетку бросали, а где рисовали из головы. Честная случайная последовательность выдавала себя длинными сериями одинаковых значений, в частности там было семь орлов (или решек, не помню уже) подряд. Товарищи, которые последовательность придумывали, старались, чтобы она выглядела послучайней, поэтому избегали длинных повторов. Максимальная серия одинаковых значений у них была всего в четыре монетки длиной. Но при ста подбрасываниях монетки вероятность получить семь или больше одинаковых значений подряд гораздо больше, чем иметь максимальную серию в четыре или меньше повторяющихся исходов.
Я сразу взялся за карандаш и клавиатуру, чтоб подсчитать эти вероятности. Вероятность в ста подбрасываниях монетки получить серию в семь или больше одинаковых значений подряд равна 54%, а вероятность получить максимальную серию в четыре или меньше всего лишь 2.83%
aknew
13.11.2018 15:53А с генератором случайных чисел такую штуку не пробовали повторить? Там ведь псевдослучайные числа и, возможно, тоже всплывет эффект как с написанными студентами подбрасываниями

mao_zvezdun
13.11.2018 16:20+1Конечно, я написал пару скриптов и погонял их. Генераторы ПСЧ не настолько уж плохи, чтобы всплывали такие эффекты. Нет, все вполне соответствует расчетам. Я потом еще, специально для друзей, кто не доверяет формулам и моделированию, сделал «натурный» эксперимент. Ну реально взял мешок монеток и подбрасывал их. Мне не пришлось даже сотню раз подкидывать. У меня седьмой решкой подряд вверх упала сорок четвертая монетка. Хотя тут повезло, конечно. Под спойлером пара картинок
теория и практика
С накоплением

Вот как-то так:


S_A
13.11.2018 15:36Интересно пишете! Но кроме максимального правдоподобия часто используют максимум апостериори. Если далее упомянете, думаю будет полнее картина вопроса. Правда это уже не совсем про МНК…

haqreu Автор
13.11.2018 18:00Ну, в принципе, MAP и MLE это практически одно и то же…

S_A
14.11.2018 04:05С точностью до одного проворота ручки Байеса. В машинном обучении максимизация апостериорной вероятности позволяет получать параметры, которые лучше позволяют обобщить (и выходит экстрапллировать) данные. Лучше, значит что выбирается одна из более вероятных гипотез. MAP технически же это MLE со штрафом на параметры.
Навскидку, R-квадрат для квартета энскомба одинаковый, то и MLE тоже будет, а MAP — разный.

gapel
13.11.2018 15:51Спасибо за статью. Чтобы вспомнить о освежить в голове тервер прекрасное чтение.
Чуть-чуть попридираюсь — данная статья относится к C++, так же как и к Python, так же и к другим языкам программирования ))

ser-mk
15.11.2018 01:46В случае же когда плотность (совсем) не гауссова, МНК дают оценку, отличающуюся от оценки MLE (maximum likehood estimation)
Если по простому не для математиков… Как в случае такой плотности быть?!
haqreu Автор
15.11.2018 09:35Если распределение известно, то хоть оно и не гауссово, ничто не мешает максимизировать правдоподобие. Это будут не МНК, а другая оптимизация, но вполне делается.


lryzhik
прошу прощения, подпись в картинке в конце главы "что изучает теорвер" — неправильная в последнем квадратике, дважды P(a) вместо P(a) + P(b)
haqreu Автор
поправил, спасибо