Почему теории Витгенштейна остаются основой всего современного NLP

Векторное представление слов — пожалуй, одна из самых красивых и романтичных идей в истории искусственного интеллекта. Философия языка — это раздел философии, исследующий связь между языком и реальностью и как сделать сделать речь осмысленной и понятной. А векторное представление слов — очень специфический метод в современной обработке естественного языка (Natural Language Processing, NLP). В некотором смысле он представляет собой эмпирическое доказательство теорий Людвига Витгенштейна, одного из самых актуальных философов прошлого века. Для Витгенштейна использование слов — это ход в социальной языковой игре, в которую играют члены сообщества, понимающие друг друга. Значение слова зависит только от его полезности в контексте, оно не соотносится один к одному с объектом из реального мира.

Для большого класса случаев, в которых мы используем слово «значение», его можно определить как значение слова есть его использование в языке.

Конечно, понять точное значение слова очень сложно. Следует учесть множество аспектов:

• к какому объекту слово, возможно, относится;
• какая это часть речи;
• является ли оно идиоматическим выражением;
• все оттенки смыслов;
• и так далее.

Все эти аспекты, в конце концов, сводятся к одному: знать, как использовать слово.

Концепция значения и почему упорядоченный набор символов имеет определённую коннотацию в языке — это не только философский вопрос, но и, вероятно, самая большая проблема, с которой приходится сталкиваться специалистам по ИИ, работающим с NLP. Русскоязычному человеку вполне очевидно, что «собака» — это «животное», и она больше похожа на «кошку», чем на «дельфина», но эта задача далеко не проста для систематического решения.

Немного подкорректировав теории Витгенштейна, можно сказать, что собаки похожи на кошек, потому что они часто появляются в одних и тех же контекстах: скорее можно найти собак и кошек, связанных со словами «дом» и «сад», чем со словами «море» и «океан». Именно эта интуиция заложена в основу Word2Vec, одной из самых известных и успешных реализаций векторного представления слов. Сегодня машины далеки от действительного понимания длинных текстов и отрывков, но векторное представление слов — бесспорно, единственный метод, который позволил сделать самый большой шаг в этом направлении за последнее десятилетие.

От BoW к Word2Vec

Во многих компьютерных задачах первая проблема — представить данные в числовой форме; слова и предложения, вероятно, сложнее всего представить в таком виде. В нашей настройке из словаря выбирается D слов, а каждому слову может быть присвоен числовой индекс i.

В течение многих десятилетий был принят классический подход представлять каждое слово как числовой D-мерный вектор из всех нулей, кроме единицы в позиции i. В качестве примера рассмотрим словарь из трёх слов: «собака», «кошка» и «дельфин» (D=3). Каждое слово может быть представлено в виде трёхмерного вектора: «собака» соответствует [1,0,0], «кошка» — [0,1,0], а «дельфин», очевидно, [0,0,1]. Документ можно представить в виде D-мерного вектора, где каждый элемент считает вхождения i-го слова в документе. Эта модель называется Bag-of-words (BoW), и она использовалась десятилетиями.

Несмотря на свой успех в 90-е годы, у BoW отсутствовала единственная интересная функция слов: их смысл. Мы знаем, что два очень разных слова могут иметь схожие значения, даже если они полностью отличаются с орфографической точки зрения. «Кошка» и «собака» оба представляют собой домашних животных, «король» и «королева» близки друг к другу, «яблоко» и «сигарета» совершенно не связаны. Мы это знаем, но в модели BoW все эти слова находятся на одинаковом расстоянии в векторном пространстве: 1.

Та же проблема распространяется на документы: с помощью BoW можно сделать вывод о схожести документов только в том случае, если они содержат одно и то же слово определённое количество раз. И вот тут приходит Word2Vec, привнося в термины машинного обучения много философских вопросов, над которыми рассуждал Витгенштейн в своих «Философских исследованиях» 60 лет назад.

В словаре размером D, где слово идентифицируется по его индексу, цель состоит в вычислении N-мерного векторного представления каждого слова при N<<D. В идеале мы хотим, чтобы это был плотный вектор, представляющий некоторые семантически-специфические аспекты значения. Например, мы в идеале хотим, чтобы «собака» и «кошка» имели схожие представления, а «яблоко» и «сигарета» — очень далёкие в векторном пространстве.

Мы хотим выполнять некоторые основные алгебраические операции над векторами, такие как король+женщина?мужчина=королева. Хочется, чтобы расстояние между векторами «актёр» и «актриса» в значительной степени совпадало с расстоянием между «принцем» и «принцессой». Несмотря на то, что эти результаты довольно утопичны, эксперименты показывают, что векторы Word2Vec проявляют свойства, очень близкие к этим.

Word2Vec не обучается этим представления напрямую, но получает их как побочный результат классификации без учителя. Средний набор данных корпуса слов NLP состоит из набора предложений; каждое слово из предложения появляется в контексте окружающих слов. Цель классификатора состоит в том, чтобы предсказать целевое слово, учитывая контекстные слова в качестве входных данных. Для предложения «коричневый пёс играет в саду» слова [коричневый, играет, в, саду] предоставляются модели в качестве входных данных, и она должна предсказать слово «пёс». Эта задача рассматривается как обучение без учителя, поскольку корпус не нужно маркировать внешним источником истины: при наличии набора предложений всегда можно автоматически создавать положительные и отрицательные примеры. Рассматривая «коричневый пёс играет в саду» в качестве положительного примера, мы можем создать множество отрицательных образцов, таких как «коричневый самолёт играет в саду» или «коричневый виноград играет в саду», заменив целевое слово «пёс» случайными словами из набора данных.

И теперь совершенно ясно применение теорий Витгенштейна: контекст имеет решающее значение для векторного представления слов, поскольку в его теориях важно прикрепить смысл к слову. Если два слова имеют схожие значения, они будут иметь схожие представления (небольшое расстояние в N-мерном пространстве) только потому, что часто появляются в похожих контекстах. Таким образом, «кошка» и «собака» в конечном итоге будут иметь близкие векторы, потому что часто появляются в одних и тех же контекстах: для модели полезно использовать для них аналогичные векторные представления, потому что это самое удобное, что она может сделать, чтобы получить лучшие результаты в прогнозировании двух слов с учётом их контекстов.

В оригинальной статье предлагаются две различные архитектуры: CBOW и Skip-gram. В обоих случаях словесные представления обучаются вместе с конкретной задачей классификации, обеспечивая наилучшие возможные векторные представления слов, которые максимизируют производительность модели.


Рисунок 1. Сравнение архитектур CBOW и Skip-gram

CBOW означает Continuous Bag of Words, и её задача — угадать слово с учётом контекста в качестве входных данных. Входы и выходы представлены как D-мерные векторы, которые проецируются в N-мерном пространстве с общими весами. Мы ищем только веса для проецирования. По сути, векторное представление слов — это матрицы D?N, где каждая строка представляет слово словаря. Все слова контекста проецируются в одну позицию, а их векторные представления усредняются; поэтому порядок слов не влияет на результат.

Skip-gram делает то же самое, но наоборот: пытается предсказать контекстные слова C, принимая в качестве входных данных целевое слово. Задача прогнозирования нескольких контекстных слов может быть переформулирована в набор независимых задач бинарной классификации, и теперь цель состоит в том, чтобы предсказать наличие (или отсутствие) контекстных слов.

Как правило, Skip-gram требует больше времени для обучения и часто даёт немного лучшие результаты, но, как обычно, у разных приложений разные требования, и трудно заранее предсказать, какие из них покажут лучший результат. Несмотря на простоту концепции, обучение архитектур такого рода — настоящий кошмар из-за количества данных и вычислительной мощности, необходимой для оптимизации весов. К счастью, в интернете можно найти некоторые предварительно обученные векторные представления слов, и можно изучать векторное пространство — самое интересное — всего несколькими строчками кода на Python.

Возможные улучшения: GloVe и fastText

Поверх классического Word2Vec в последние годы предложено множество возможных улучшений. Два наиболее интересных и часто используемых — это GloVe (Стэнфордский университет) и fastText (разработанный Facebook). Они пытаются выявить и преодолеть ограничения оригинального алгоритма.

В оригинальной научной статье авторы GloVe подчёркивают, что обучение модели на отдельном локальном контексте плохо использует глобальную статистику корпуса. Первый шаг для преодоления этого ограничения — создание глобальной матрицы X, где каждый элемент i,j подсчитывает количество упоминаний слова j в контексте слова i. Вторая важная идея этого документа — понимание, что только одних вероятностей недостаточно для надёжного предсказания значений, а требуется ещё матрица совместного вхождения, откуда можно напрямую извлекать определённые аспекты значений.

Рассмотрим два слова i и j, которые представляют особый интерес. Для конкретности предположим, что нас интересует понятие термодинамического состояния, для которого можно взять i = лёд и j = пар. Связь этих слов можно исследовать, изучая соотношение их вероятностей совместного появления с помощью разных зондирующих словами, k. Для слов k, связанных со льдом, но не паром, скажем k = тело [твёрдое тело, состояние вещества], мы ожидаем, что отношение Pik/Pjk окажется больше. Аналогично, для слов k, связанных с паром, но не со льдом, скажем k = газ, отношение должно быть небольшим. Для слов вроде «вода» или «мода», которые или одинаково связаны со льдом и паром, или не имеют к ним отношения, это отношение должно быть близко к единице.

Такое соотношение вероятностей становится отправной точкой для изучения векторного представления слов. Мы хотим иметь возможность вычислять векторы, которые в сочетании с конкретной функцией F поддерживают это соотношение постоянным в пространстве векторного представления.


Рисунок 2. Наиболее общая формула для векторного представления слов в модели GloVe

Функцию F и зависимость от слова k можно упростить, заменив экспонентами и фиксированными смещениями, что даёт в результате функцию минимизации ошибок по методу наименьших квадратов J:


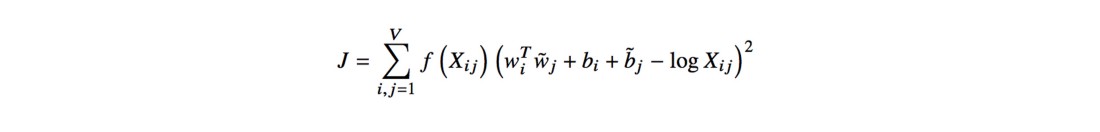
Рисунок 3. Итоговая функция вычисления векторного представления слов в модели GloVe

Функция f — это функция подсчёта, которая пытается не утяжелять очень частые и редкие совпадения, в то время как bi и bj представляют собой смещения для восстановления симметрии функции. В последних абзацах статьи показано, что обучение этой модели в итоге не сильно отличается от обучения классической модели Skip-gram, хотя в эмпирических тестах GloVe превосходит обе реализации Word2Vec.

С другой стороны, fastText исправляет совершенно другой недостаток Word2Vec: если обучение модели начинается с прямого кодирования одного D-мерного вектора, то игнорируется внутренняя структура слов. Вместо прямого кодирования кодирования слов, изучающих словесные представления, fastText предлагает изучать N-граммы символов и представлять слова как сумму векторов N-грамм. Например, при N=3 слово «flower» кодируется как 6 различных 3-грамм [<fl, flo, low, Debt, wer, er>] плюс специальная последовательность <flower>. Обратите внимание, как угловые скобки используются для обозначения начала и конца слова. Таким образом, слово представлено его индексом в словаре слов и набором N-грамм, которые оно содержит, сопоставленных целым числам с помощью функции хэширования. Это простое улучшение позволяет разделить N-граммовые представления между словами и вычислить векторные представления слов, которых не было в корпусе обучения.

Эксперименты и возможные применения

Как мы уже говорили, для использования этих векторные представления нужно всего несколько строк кода на Python. Я провёл несколько экспериментов с 50-мерной моделью GloVe, обученной на 6 миллиардах слов из предложений Википедии, а также с 300-мерной моделью fastText, обученной на Common Crawl (что дало 600 миллиардов токенов). В этом параграфе указаны ссылки на результаты обоих экспериментов только для того, чтобы доказать концепции и дать общее понимание темы.

Прежде всего, я хотел проверить некоторые основные сходства слов, простейшую, но важную особенность их векторного представления. Как и ожидалось, наиболее схожими словами со словом «собака» оказались «кошка» (0.92), «собаки» (0.85), «лошадь» (0.79), «щенок» (0.78) и «домашнее животное» (0.77). Обратите внимание, что форма множественного числа имеет почти то же значение, что и единственное число. Опять же, для нас довольно тривиально так говорить, но для машины это совершенно не факт. Теперь еда: самые похожие слова для «пиццы» это «сэндвич» (0.87), «сэндвичи» (0.86), «закуска» (0.81), «выпечка» (0.79), «фри» (0.79) и «бургеры» (0.78). Имеет смысл, результаты удовлетворительные, и модель ведёт себя довольно хорошо.

Следующий шаг — выполнить в векторном пространстве некоторые базовые вычисления и проверить, насколько правильно модель усвоила некоторые важные свойства. И действительно, в результате вычисления векторов женщина+актер-мужчина получается результат «актриса» (0.94), а в результате вычисления мужчина+королева-женщина — слово «король» (0.86). Вообще говоря, если значение a:b=c:d, слово d должно быть получено как d=b-a+c. Переходя на следующий уровень, невозможно представить, как эти векторные операции описывают даже географические аспекты: мы знаем, что Рим является столицей Италии, так как Берлин является столицей Германии, на самом деле Берлин+Италия-Рим=Германия (0.88), а Лондон+Германия-Англия=Берлин (0.83).

А теперь самое интересное. Следуя той же идее, попробуем складывать и вычитать понятия. Например, Что такое американский эквивалент пиццы для итальянцев? пицца+Америка-Италия=бургеры (0.60), затем чизбургеры (0.59). С тех пор как я переехал в Голландию, я всегда говорю, что эта страна — смесь трёх вещей: немного американского капитализма, шведского холода и качества жизни, и, наконец, щепотка неаполитанского изобилия. Немного изменив первоначальную теорему, удалив немного швейцарской точности, мы получаем Голландию (0.68) как результат США+Швеция+Неаполь-Швейцария: довольно впечатляюще, если честно.


Рисунок 4. Всем голландским читателям: примите это как комплимент, ладно?

Для использования этих предварительно обученных векторных представлений хорошие практические ресурсы можно найти здесь и здесь. Gensim — простая и полная библиотека на Python с некоторыми готовыми к использованию алгебраическими функциями и функциями подобия. Эти предварительно обученные векторные представления можно использовать различными (и полезными) способами, например для улучшения производительности анализаторов настроения или языковых моделей. Какова бы ни была задача, использование N-мерных векторов значительно улучшит эффективность модели по сравнению с прямым кодированием. Конечно, обучение на векторных представлениях в специфической области ещё больше улучшит результат, но для этого могут потребоваться, пожалуй, чрезмерные усилия и время.