Введение

Умножение матриц — это один из базовых алгоритмов, который широко применяется в различных численных методах, и в частности в алгоритмах машинного обучения. Многие реализации прямого и обратного распространения сигнала в сверточных слоях неронной сети базируются на этой операции. Так порой до 90-95% всего времени, затрачиваемого на машинное обучение, приходится именно на эту операцию. Почему так происходит? Ответ кроется в очень эффективной реализации этого алгоритма для процессоров, графических ускорителей (а в последнее время и специальных ускорителей матричного умножения). Матричное умножение — один из немногих алгоритмов, которые позволяет эффективно задействовать все вычислительные ресурсы современных процессоров и графических ускорителей. Поэтому не удивительно, что многие алгоритмы стараются свести к матричному умножению — дополнительная расходы, связанные с подготовкой данных, как правило с лихвой окупаются общим ускорением алгоритмов.

Так как реализован алгоритм матричного умножения? Хотя сейчас существуют множество реализаций данного алгоритма, в том числе и в открытых исходных кодах. Но к сожалению, код данных реализаций (большей частью на ассемблере) весьма сложен. Существует хорошая англоязычная статья, подробно описывающая эти алгоритмы. К моему удивлению, я не обнаружил аналогов на Хабре. Как по мне, этого повода вполне достаточно, чтобы написать собственную статью. С целью ограничить объем изложения, я ограничился описанием однопоточного алгоритма для обычных процессоров. Тема многопоточности и алгоритмов для графических ускорителей явно заслуживает отдельной статьи.

Процесс изложения будет вестись ввиде шагов с примерами по последовательному ускорению алгоритма. Я старался писать максимально упрощая задачу, но не более того. Надеюсь у меня получилось…

Постановка задачи (0-й шаг)

В общем случае функция матричного умножения описывается как:

C[i,j] = a*C[i,j] + b*Sum(A[i,k]*B[k,j]);

Где матрица A имеет размер M х K, матрица B — K х N, и матрица C — M х N.



Мы без ущерба для изложения, можем считать, что a = 0 и b = 1:

C[i,j] = Sum(A[i,k]*B[k,j]);

Ее реализация на С++ «в лоб» по формуле будет выглядеть следующим образом:

void gemm_v0(int M, int N, int K, const float * A, const float * B, float * C)
{
    for (int i = 0; i < M; ++i)
    {
        for (int j = 0; j < N; ++j)
        {
            C[i*N + j] = 0;
            for (int k = 0; k < K; ++k)
                C[i*N + j] += A[i*K + k] * B[k*N + j];
        }
    }
}

Глупо было бы ожидать от нее какой-либо производительности, и действительно тестовые замеры показывают, что при (M=N=K=1152) она выполняется почти 1.8 секунды (тестовая машина — i9-7900X@3.30GHz, ОС — Ubuntu 16.04.6 LTS, компилятор — g++-6.5.0б опции компилятора — "-fPIC -O3 -march=haswell"). Минимальное количество операций для матричного умножения — 2*M*N*K = 2*10^9. Иначего говоря, производительность составляет 1.6 GFLOPS, что очень далеко от теоретического предела однопоточной производительности для данного процессора (~120 GFLOPS (float-32) если ограничится использованием AVX2/FMA и ~200 GFLOPS при использовании AVX-512). Так, что нужно предпринять, чтобы приблизится к теоретическому пределу? Далее мы в ходе ряда последовательных оптимизаций придем к решению, которое во многом воспроизводит то, что используется во многих стандартных библиотеках. В процессе оптимизации, я буду задействовать только AVX2/FMA, AVX-512 я касаться не буду, так как их распостраненность пока невелика.

Устраняем очевидные недостатки (1-й шаг)

Сначала устраним самые очевидные недостатки алгоритма:

1. Вычисление адресов элементов массивов можно упростить — вынести постоянную часть из внутреннего цикла.
2. В оригинальной версии доступ к элементам массива B производится не последовательно. Его можно упорядочить, если поменять порядок вычисления таким образом, чтобы внутренним циклом был последовательный обход по строчкам для всех трех матриц.

void gemm_v1(int M, int N, int K, const float * A, const float * B, float * C)
{
    for (int i = 0; i < M; ++i)
    {
        float * c = C + i * N;
        for (int j = 0; j < N; ++j)
            c[j] = 0;
        for (int k = 0; k < K; ++k)
        {
            const float * b = B + k * N;
            float a = A[i*K + k];
            for (int j = 0; j < N; ++j)
                c[j] += a * b[j];
        }
    }
}

Результат тестовых замеров показывает время выполнения в 250 мс, или 11.4 GFLOPS. Т.е. такими небольшими правками мы получили ускорение в 8 раз!

Векторизуем внутренний цикл (2-й шаг)

Если внимательно посмотреть на внутренний цикл (по переменной j), то видно, что вычисления можно проводить блоками (векторами). Практически все современные процессоры позволяют проводить вычисления над такими векторами. В частности набор инструкций AVX оперирует с векторами размерностью 256 бит. Что позволяет выполнить 8 операций для вещественных чисел с одинарной точностью за такт. AVX2/FMA делает еще один шаг вперед — он позволяет выполнить слитную операцию умножения и сложения (d = a*b + c) над вектором. Настольные процессоры Интел начиная с 4-го поколения имеют 2 256-bit FMA модуля, что позволяет им теоретически выполнять 2*2*8 = 32 операции (float-32) за такт. К счастью, инструкции AVX2/FMA достаточно легко задействовать напрямую из С/С++ при помощи встроенных функций (intrinsics). Для AVX2/FMA они объявлены в заголовочном файле <immintrin.h>.

void gemm_v2(int M, int N, int K, const float * A, const float * B, float * C)
{
    for (int i = 0; i < M; ++i)
    {
        float * c = C + i * N;
        for (int j = 0; j < N; j += 8)
            _mm256_storeu_ps(c + j + 0, _mm256_setzero_ps());
        for (int k = 0; k < K; ++k)
        {
            const float * b = B + k * N;
            __m256 a = _mm256_set1_ps(A[i*K + k]);
            for (int j = 0; j < N; j += 16)
            {
                _mm256_storeu_ps(c + j + 0, _mm256_fmadd_ps(a, 
                    _mm256_loadu_ps(b + j + 0), _mm256_loadu_ps(c + j + 0)));
                _mm256_storeu_ps(c + j + 8, _mm256_fmadd_ps(a, 
                    _mm256_loadu_ps(b + j + 8), _mm256_loadu_ps(c + j + 8)));
            }
        }
    }
}

Запускаем тесты, получаем время 217 мс или 13.1 GFLOPS. Упс! Ускорение всего на 15%. Какже так? Тут нужно учитывать, два фактора:

1. Компиляторы нынче умные пошли (не все!), и вполне справляются с задачей автовекторизации простых циклов. Уже в 1-м варианте компилятор фактически задействовал инструкции AVX2/FMA, потому ручная оптимизация не дала нам практически никаких преимуществ.
2. Скорость расчетов в данном случае упирается не в вычислителные возможности процессора, а в скорость загрузки и выгрузки данных. В данном случае процессору для задействования 2 256-bit FMA блоков требуется загрузить 4 и выгрузить 2 256-bit вектора за такт. Это в два раза превышает даже пропускную способность L1 кеша процессора (512/256 bit), не говоря уже о пропускной способности памяти, которая еще на порядок меньше (64-bit на канал)).

Итак, основная проблема в ограниченной пропускной способности памяти в современных процессорах. Процессор фактически простаивает 90% времени, ожидая, когда данные загрузятся и сохранятся в памяти.

Дальнейшие наши шаги по оптимизации алгоритма будут направлены на минимизацию доступа в память.

Пишем микроядро (3-й шаг)

В предыдущей версии на 1 FMA операцию приходится 2 загрузки и 1 выгрузка.
Больше всего загрузок и выгрузок происходит с результирующей матрицей С: данные из нее нужно загрузить, прибавить к ним произведение C[i][j] += A[i][k]*B[k][j], а потом сохранить. И так много раз. Наиболее быстрая память, с которой может работать процессор — это его собственные регистры. Если мы будем хранить результирующее значение матрицы С в регистре процессора, то в процессе расчета нужно будет подгружать только значение матриц A и B. Теперь у нас на 1 FMA операцию приходится только 2 загрузки.

Если мы будем хранить в регистрах значения двух соседних столбцов матрицы C[i][j] и C[i][j+1], то сможем повторно использовать загруженное значение матрицы A[i][k]. И на 1 FMA операцию потребуется только 1.5 загрузки. Кроме того, сохраняя результат в 2 независимых регистра, мы позволим процессору выполнять 2 FMA операции за такт. Аналогично можно хранить в регистрах значения двух соседних строк — тогда будет осуществляться экономия на загрузке значений матрицы B.



Всего настольные процессоры Интел начиная с 2-го поколения имеют 16 256-bit векторных регистров (справедливо для 64-bit режима процессора). 12 из них можно использовать для хранения кусочка результирующей матрицы С размером 6x16. В итоге мы сможем выполнить 12*8 = 96 FMA операций загрузив из памяти только 16 + 6 = 22 значений. И того нам удалось сократить доступ к памяти с 2.0 до 0.23 загрузки на 1 FMA операцию — почти в 10 раз!

Функция которая осуществляет вычисление такого маленького кусочка матрицы С, обычно называется микроядром, ниже приведен пример такой функции:

void micro_6x16(int K, const float * A, int lda, int step, 
    const float * B, int ldb, float * C, int ldc)
{
    __m256 c00 = _mm256_setzero_ps();
    __m256 c10 = _mm256_setzero_ps();
    __m256 c20 = _mm256_setzero_ps();
    __m256 c30 = _mm256_setzero_ps();
    __m256 c40 = _mm256_setzero_ps();
    __m256 c50 = _mm256_setzero_ps();
    __m256 c01 = _mm256_setzero_ps();
    __m256 c11 = _mm256_setzero_ps();
    __m256 c21 = _mm256_setzero_ps();
    __m256 c31 = _mm256_setzero_ps();
    __m256 c41 = _mm256_setzero_ps();
    __m256 c51 = _mm256_setzero_ps();
    const int offset0 = lda * 0;
    const int offset1 = lda * 1;
    const int offset2 = lda * 2;
    const int offset3 = lda * 3;
    const int offset4 = lda * 4;
    const int offset5 = lda * 5;
    __m256 b0, b1, a0, a1;
    for (int k = 0; k < K; k++)
    {
        b0 = _mm256_loadu_ps(B + 0);
        b1 = _mm256_loadu_ps(B + 8);
        a0 = _mm256_set1_ps(A[offset0]);
        a1 = _mm256_set1_ps(A[offset1]);
        c00 = _mm256_fmadd_ps(a0, b0, c00);
        c01 = _mm256_fmadd_ps(a0, b1, c01);
        c10 = _mm256_fmadd_ps(a1, b0, c10);
        c11 = _mm256_fmadd_ps(a1, b1, c11);
        a0 = _mm256_set1_ps(A[offset2]);
        a1 = _mm256_set1_ps(A[offset3]);
        c20 = _mm256_fmadd_ps(a0, b0, c20);
        c21 = _mm256_fmadd_ps(a0, b1, c21);
        c30 = _mm256_fmadd_ps(a1, b0, c30);
        c31 = _mm256_fmadd_ps(a1, b1, c31);
        a0 = _mm256_set1_ps(A[offset4]);
        a1 = _mm256_set1_ps(A[offset5]);
        c40 = _mm256_fmadd_ps(a0, b0, c40);
        c41 = _mm256_fmadd_ps(a0, b1, c41);
        c50 = _mm256_fmadd_ps(a1, b0, c50);
        c51 = _mm256_fmadd_ps(a1, b1, c51);
        B += ldb; A += step;
    }
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c00, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c01, _mm256_loadu_ps(C + 8)));
    C += ldc;
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c10, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c11, _mm256_loadu_ps(C + 8)));
    C += ldc;
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c20, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c21, _mm256_loadu_ps(C + 8)));
    C += ldc;
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c30, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c31, _mm256_loadu_ps(C + 8)));
    C += ldc;
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c40, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c41, _mm256_loadu_ps(C + 8)));
    C += ldc;
    _mm256_storeu_ps(C + 0, _mm256_add_ps(c50, _mm256_loadu_ps(C + 0)));
    _mm256_storeu_ps(C + 8, _mm256_add_ps(c51, _mm256_loadu_ps(C + 8)));
}

Введем небольшую вспомогательную функцию для инициализации начального значения матрицы С:

void init_c(int M, int N, float * C, int ldc)
{
    for (int i = 0; i < M; ++i, C += ldc)
        for (int j = 0; j < N; j += 8)
            _mm256_storeu_ps(C + j, _mm256_setzero_ps());
}

Здесь lda, ldb, ldc — длина строчки (Leading Dimension в общем случае) соответсвующей матрицы.

Тогда функция умножения примет следующий вид:

void gemm_v3(int M, int N, int K, const float * A, const float * B, float * C)
{
    for (int i = 0; i < M; i += 6)
    {
        for (int j = 0; j < N; j += 16)
        {
            init_c(6, 16, C + i*N + j, N);
            micro_6x16(K, A + i*K, K, 1, B + j, N, C + i*N + j, N);
        }
    }
}

Запускаем ее и получаем время исполнения 78.5 мс или 36.2 GFLOPS. Т.е. использование микроядра позволило ускорить матричное умножение почти в 3 раза. Но полученное быстродействие все еще далеко от максимального. Где теперь узкое место?

Переупорядочиваем матрицу B (4-й шаг)

Микроядро за каждую итерацию загружает два 256-bit вектора из матрицы B.



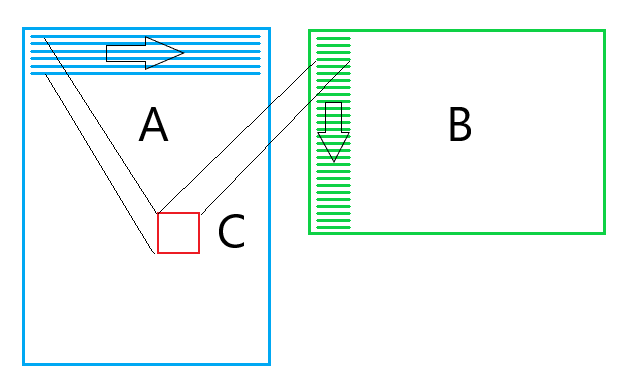
Причем каждый раз из новой строчки. Это делает невозможным для процессора эффективное кеширование этих данных. Для исправления этой ситуации сделаем два изменения:

1. Скопируем данные матрицы B во временный буфер таким образом, чтобы данные, необходимые одному микроядру лежали рядом.
2. Изменим порядок обхода матрицы С: сначала будем ходить по столбцам и только потом по строкам. Это позволит эффективнее использовать переупорядоченные значения матрицы B.

Для хранения буфера заведем небольшую структуру:

struct buf_t
{
    float * p;
    int n;

    buf_t(int size) : n(size), p((float*)_mm_malloc(size * 4, 64)) {}
    ~buf_t() { _mm_free(p); }
};

Здесь стоит отметить, что загрузка и выгрузка AVX векторов оптимально работает при выровненных данных, потому используются специальные функции для выделения памяти.

Функция переупорядочивания матрицы B:

void reorder_b_16(int K, const float * B, int ldb, float * bufB)
{
    for (int k = 0; k < K; ++k, B += ldb, bufB += 16)
    {
        _mm256_storeu_ps(bufB + 0, _mm256_loadu_ps(B + 0));
        _mm256_storeu_ps(bufB + 8, _mm256_loadu_ps(B + 8));
    }
}

Ну и собственно 4-я версия функции gemm:

void gemm_v4(int M, int N, int K, const float * A, const float * B, float * C)
{
    for (int j = 0; j < N; j += 16)
    {
        buf_t bufB(16*K);
        reorder_b_16(K, B + j, N, bufB.p);
        for (int i = 0; i < M; i += 6)
        {
            init_c(6, 16, C + i*N + j, N);
            micro_6x16(K, A + i*K, K, 1, bufB.p, 16, C + i*N + j, N);
        }
    }
}

Результаты тестирования (29.5 мс или 96.5 GFLOPS) показывают, что мы на правильном пути. Фактически достигнуто около 80% от теоретически возможного максимума.

Победа? К сожалению нет. Просто размер матриц, который мы использовали для тестирования (M=N=K=1152) оказался удобным для данной версии алгоритма. Если увеличить К в 100 раз (M=1152, N=1152, K=115200), то эффективность алгоритма упадет до 39.5 GFLOPS — почти в 2.5 раза.

Локализуем данные в кэше L1 (5-й шаг)

Так почему же с ростом параметра K, падает эффективность алгоритма? Ответ кроется в величине буфера, который мы использовали для хранения переупорядоченных значений B. При больших значениях K он просто не влазит в кэш процессора. Решением проблемы будет ограничение его величины до размера кэша данных L1. Для процессоров Интел размер кэша данных L1 составляет 32 kb. C ограничением размера буфера, микроядро будет пробегать не по всем значениям K, а только по диапазону, который влазит в L1 кэш. Результаты промежуточных расчетов матрицы С будут храниться в основной памяти.

Введем макроядро — вспомогательную функцию, которая производит расчеты над областью данных, которые влазят в кэш:

void macro_v5(int M, int N, int K, const float * A, int lda, 
    const float * B, int ldb, float * bufB, float * C, int ldc)
{
    for (int j = 0; j < N; j += 16)
    {
        reorder_b_16(K, B + j, ldb, bufB);
        for (int i = 0; i < M; i += 6)
            micro_6x16(K, A + i*lda, lda, 1, bufB, 16, C + i*ldc + j, ldc);
    }
}

В главной функции у нас добавится цикл по K, в котором мы будем вызывать макроядро:

void gemm_v5(int M, int N, int K, const float * A, const float * B, float * C)
{
    const int L1 = 32 * 1024;
    int mK = std::min(L1 / 4 / 16, K);
    buf_t bufB(16 * mK);
    for(int k = 0; k < K; k += mK)
    {
        int dK = std::min(K, k + mK) - k;
        if(k == 0)
            init_c(M, N, C, N);
        macro_v5(M, N, dK, A + k, K, B + k*N, N, bufB.p, C, N);
    }
}

Результаты замеров показывают, что мы движемся в правильном направлении: для (M=1152, N=1152, K=115200) производительность алгоритма составила 78.1 GFLOPS. Это значительно лучше, чем в прошлой версии, но все еще хуже, чем для матрицы средних размеров.

Переупорядочиваем матрицу A и локализуем в кэше L2 (6-й шаг)

Ограничив размер K, который обрабатывается за один проход микроядра, мы сумели локализовать данные матрицы B в кэше L1. Данных, которые подгружаются из матрицы A почти в три раза меньше. Но давайте попробуем локализовать и их, заодно переупорядочив данные, чтобы они лежали последовательно. Напишем для этого специальную функцию:

void reorder_a_6(const float * A, int lda, int M, int K, float * bufA)
{
    for (int i = 0; i < M; i += 6)
    {
        for (int k = 0; k < K; k += 4)
        {
            const float * pA = A + k;
            __m128 a0 = _mm_loadu_ps(pA + 0 * lda);
            __m128 a1 = _mm_loadu_ps(pA + 1 * lda);
            __m128 a2 = _mm_loadu_ps(pA + 2 * lda);
            __m128 a3 = _mm_loadu_ps(pA + 3 * lda);
            __m128 a4 = _mm_loadu_ps(pA + 4 * lda);
            __m128 a5 = _mm_loadu_ps(pA + 5 * lda);
            __m128 a00 = _mm_unpacklo_ps(a0, a2);
            __m128 a01 = _mm_unpacklo_ps(a1, a3);
            __m128 a10 = _mm_unpackhi_ps(a0, a2);
            __m128 a11 = _mm_unpackhi_ps(a1, a3);
            __m128 a20 = _mm_unpacklo_ps(a4, a5);
            __m128 a21 = _mm_unpackhi_ps(a4, a5);
            _mm_storeu_ps(bufA + 0, _mm_unpacklo_ps(a00, a01));
            _mm_storel_pi((__m64*)(bufA + 4), a20);
            _mm_storeu_ps(bufA + 6, _mm_unpackhi_ps(a00, a01));
            _mm_storeh_pi((__m64*)(bufA + 10), a20);
            _mm_storeu_ps(bufA + 12, _mm_unpacklo_ps(a10, a11));
            _mm_storel_pi((__m64*)(bufA + 16), a21);
            _mm_storeu_ps(bufA + 18, _mm_unpackhi_ps(a10, a11));
            _mm_storeh_pi((__m64*)(bufA + 22), a21);
            bufA += 24;
        }
        A += 6 * lda;
    }
}

Так как, данные матрицы A теперь идут последовательно, то параметр lda в макроядре нам больше не нужен. Также поменялись параметры вызова микроядра:

void macro_v6(int M, int N, int K, const float * A, 
    const float * B, int ldb, float * bufB, float * C, int ldc)
{
    for (int j = 0; j < N; j += 16)
    {
        reorder_b_16(K, B + j, ldb, bufB);
        for (int i = 0; i < M; i += 6)
            micro_6x16(K, A + i*K, 1, 6, bufB, 16, C + i*ldc + j, ldc);
    }
}

Размер буфера для переупорядоченной матрицы A ограничиваем размером L2 кэша процессора (он обычно составляет от 256 до 1024 kb для разных типов процессоров). В главной функции добавляется дополнительный цикл по переменной M:

void gemm_v6(int M, int N, int K, const float * A, const float * B, float * C)
{
    const int L1 = 32 * 1024, L2 = 256*1024;
    int mK = std::min(L1 / 4 / 16, K) / 4 * 4;
    int mM = std::min(L2 / 4 / mK, M) / 6 * 6;
    buf_t bufB(16 * mK);
    buf_t bufA(mK * mM);
    for(int k = 0; k < K; k += mK)
    {
        int dK = std::min(K, k + mK) - k;
        for (int i = 0; i < M; i += mM)
        {
            int dM = std::min(M, i + mM) - i;
            if (k == 0)
                init_c(dM, N, C + i * N, N);
            reorder_a_6(A + i * K + k, K, dM, dK, bufA.p);
            macro_v6(dM, N, dK, bufA.p, B + k * N, N, bufB.p, C + i * N, N);
        }
    }
}

Результаты тестовых замеров для (M=1152, N=1152, K=115200) — 88.9 GFLOPS — приблизились еще на один шаг к результату для матриц среднего размера.

Задействуем кэш L3 (7-й шаг)

В процессорах помимо кэша L1 и L2 еще часто бывает кэш L3 (обычно его размер составляет 1-2 MB на ядро). Попробуем задействовать и его, например, для хранения переупорядоченных значений матриц B, чтобы избежать лишних вызовов функции reorder_b_16. В функции макроядра появится дополнительные параметр reorderB, который будет сообщать о том, что данныe матрицы B уже упорядочены:

void macro_v7(int M, int N, int K, const float * A, 
    const float * B, int ldb, float * bufB, bool reorderB, float * C, int ldc)
{
    for (int j = 0; j < N; j += 16)
    {
        if(reorderB)
            reorder_b_16(K, B + j, ldb, bufB + K*j);
        for (int i = 0; i < M; i += 6)
            micro_6x16(K, A + i*K, 1, 6, bufB + K*j, 16, C + i*ldc + j, ldc);
    }
}

В основной функции добавится цикл по N:

void gemm_v7(int M, int N, int K, const float * A, const float * B, float * C)
{
    const int L1 = 32 * 1024, L2 = 256*1024, L3 = 2*1024*1024;
    int mK = std::min(L1 / 4 / 16, K) / 4 * 4;
    int mM = std::min(L2 / 4 / mK, M) / 6 * 6;
    int mN = std::min(L3 / 4 / mK, N) / 16 * 16;
    buf_t bufB(mN * mK);
    buf_t bufA(mK * mM);
    for (int j = 0; j < N; j += mN)
    {
        int dN = std::min(N, j + mN) - j;
        for (int k = 0; k < K; k += mK)
        {
            int dK = std::min(K, k + mK) - k;
            for (int i = 0; i < M; i += mM)
            {
                int dM = std::min(M, i + mM) - i;
                if (k == 0)
                    init_c(dM, dN, C + i * N + j, N);
                reorder_a_6(A + i * K + k, K, dM, dK, bufA.p);
                macro_v7(dM, dN, dK, bufA.p, B + k * N + j, N, 
                    bufB.p, i == 0, C + i * N + j, N);
            }
        }
    }
}

Результаты замеров для (M=1152, N=1152, K=115200) дают результат в 97.3 GFLOPS. Т.е. мы даже немного превысили результат для матриц среднего размера. Фактически мы получили универсальный алгоритм (на самом деле нет, про ограничения в следующем разделе), который практически одинаково эффективно (порядка 80% от теоретически достижимого макимума) работает для любого размера матриц. На этом предлагаю остановиться и описать, что у нас в итоге получилось.

Общая схема алгоритма

На рисунке ниже приведена схема получившегося алгоритма:

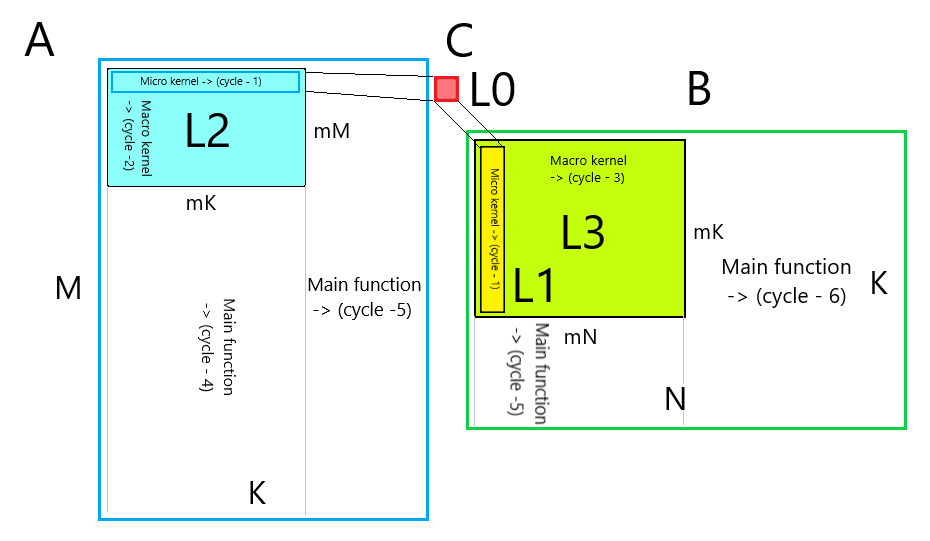
Микро ядро

• Цикл-1 по переменной k. Переупорядоченные данные из матрицы B лежат в кэше L1, переупорядоченные данные из матрицы A лежат в кэше L2. Сумма аккумулируется в регистрах (кэше L0). Результат записывается в основную память. Размеры микроядра определяются длиной SIMD вектора и количеством векторных регистров. Длина цикла определяется размером кэша L1, где хранится B.

Макро ядро

• Цикл-2 по переменной i. Пробегает микроядром по переупорядоченным данным матрицы A, которые лежат в кэше L2.
• Цикл-3 по переменной j. Пробегает микроядром по переупорядоченным данным матрицы B, которые лежат в кэше L3. Опционально переупорядочивает недостающие данные в B.

Размеры макроядра определяются величиной кэша.

Основная функция

• Цикл-4 по переменной i. Пробегает макроядром по матрице A. На каждой итерации переупорядочивает значения A. Опционально инициализирует значения матрицы С.
• Цикл-5 по переменной k. Пробегает макроядром по матрицам A и B.
• Цикл-6 по переменной j. Пробегает макроядром по матрице B.

Что осталось за кадром?

В процессе изложения основных принципов, которые используются в алгоритме матричного умножения, я сознательно упростил задачу, иначе она бы не влезла ни в одну статью. Ниже я опишу некоторые вопросы, которые неважны для понимания основной сути алгоритма, но очень важны для практической их реализации:

1. В реальности, к сожалению, размер матриц не всегда кратен размерам микроядра, потому края матриц приходится обрабатывать особым образом. Для чего приходится реализовывать микроядра разных размеров.
2. Для разных типов процессоров реализуются разные наборы микроядер и функций переупорядочивания. Также свои микроядра будет для чисел с двойной точностью и для комплексных чисел. К счастью, зоопарк микроядер ограничен только ими и на верхнем уровне код достаточно универсальный.
3. Микроядра часто пишут прямо на ассемблере. Также проводят дополнительное разворачивание циклов. Но это не приводит к существенному ускорению — основные оптимизации заключаются в эффективном использовании кэшевой иерархии памяти процессора.
4. Для матриц малого размера (по любому измерению) применяют особые алгоритмы — иногда переупорядочивание не эффективно, иногда нужно применять другой порядок обхода матриц. А иногда и реализовывать особые микроядра.
5. В обобщенном алгоритме матричного умножения все три матрицы могут быть транспонированы. Казалось бы число возможных алгоритмов возрастает в 8 раз! К счастью применение переупорядочивания входных данных, позволяет для всех случаев обойтись унивесальными микроядрами.
6. Практически все современные процессоры — многоядерны. И библиотеки матричного умножения используют многопоточность для ускорения вычислений. Обычно для этого используется еще 1-3 дополнительных цикла, в которых происходит разбиение задач по разным потокам.

Заключение

Приведенный алгоритм матричного умножения позволяет эффективно задействовать ресурсы современных процессоров. Но он наглядно показывает, что максимальная утилизация ресурсов современных процессоров — это далеко нетривиальная задача. Подход с использованием микроядер и максимальной локализации данных в кэше процессора можно с успехом использовать и для других алгоритмов.

Код проекта с алгоритмами из статьи можно найти на Github.

Надеюсь вам было интересно!