27.04.2019 19:15
Enthusiastic_programmer 22 6400 Источник
Добрый день, дорогие пользователи habr.com! Сегодня православные христиане празднуют Пасху, и мне кажется, что многие задаются вопросом: «Какой же объём у куриного (страусиного, перепелиного и т.д.) яйца»? Это действительно интересная математическая задача, которую мы с Вами постараемся решить в этой статье. Приятного чтения!

Зачем?
Эта статья поможет разобраться с формулой объема для тел вращения и нахождением значения определенных интегралов, что в дальнейшем пригодится для IT-разработок.

image

Рисунок 1. Пасхальные яйца

Начальные положения, определяемся с кривой



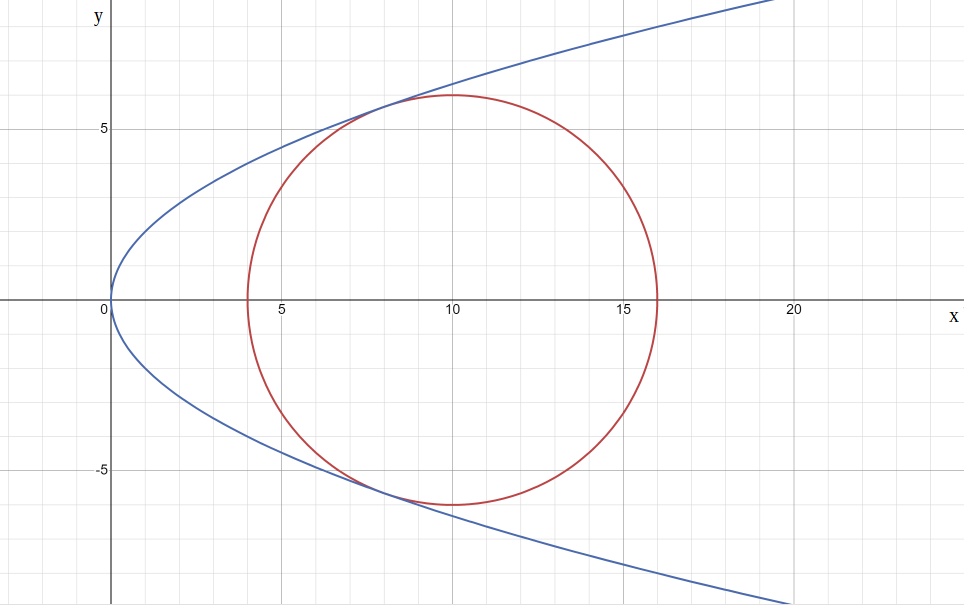
image

Рисунок 2. График яйца

Для начала определимся с функциями, которыми мы будем задавать наше яйцо.

Я предлагаю описывать наше яйцо следующей кусочно-заданной кривой:

При x ? [0, 8] cu:

$y^2 = 4x$



При x ? [8, 16] cu:

$y^2 = 36 – (x-10)^2$


(Уравнение окружности с центром в точке (10, 0) и радиусом 6.)

Чем обусловлен такой выбор? Полученная кривая в большей степени напоминает яйцо, чем любая другая кривая, составленная из двух уравнений. Точка касания окружности к кривой – целое число, она равна 8. Т. е. при дальнейшем интегрировании площади тела вращения (для нахождения объема) будем рассматривать его как сумму объемов двух различных тел вращения.

Объем тела вращения через определенный интеграл


Наша расчетная формула выглядит следующим образом:

$V = ??_a^b f(x)^2 dx$



Уравнение 1. Формула объема тела вращения

И теперь просто считаем два объема:

Для x? 0 и x ? 8:

$y^2 = 4x$


$$display$$V = ??_a^b f(x)^2 dx = ??_0^8 (4x) dx = {4?x^2\over2} = 2?x^2=128?$$display$$



Т.е. объем первой части тела вращения = 128?.

Для x?8 и x ? 16:

$y^2 = 36 – (x-10)^2$


$$display$$V = ??_a^b f(x)^2 dx = ??_8^{16} (36 – (x-10)^2) dx =$$display$$


$=?(36*16-{1 \over 3} ( 16-10 )^3 - 36*8+{1 \over 3} ( 16-8)^3)=640?/3$



Суммарный объем нашего яйца получается равным 1024?/3 у.е. или ? 1072,29 у.е.

Напомню, что все расчеты велись в условных единицах и длина (читай высота) моего яйца – 16 у.е.

Из формулы подобия следует:

${V_1 \over V_2} = k^3 $


Если ваше яйцо имеет длину, равную 58 мм, то его объем находится через пропорцию:

${1072,29 \over V_2} = ({16 \over 58})^3$



V2 = 51 см^3

Истинность данного результата подтверждена экспериментально:

image

Рисунок 3. Мензурка, вода на уровне 500 мл

image

Рисунок 4. Мензурка, вода на уровне между 500 и 600 мл

Спасибо, что прочли эту статью до конца! Светлой Пасхи Вам!

image

P.S. Автор выражает отдельную благодарность пользователю akhalat за его коррективы. Спасибо!

Комментарии (22)


  1. akhalat
    27.04.2019 22:23
    #20085184
    +10

    Что за «формула подобия» — в тексте никаких пояснений нет.
    Вообще, лучше было бы не подставлять конкретных чисел, а выразить все функции через параметр, задающий «размер яйца» — тогда на выходе была бы сразу общая формула без всяких вопросов.
    И брать второй интеграл от 8.01 — несусветная глупость. Когда считают объем «составных» тел никаких зазоров делать не надо.
    Тем более, в выражение вы подставляете точное значение «8».
    Наконец, у вас неверный расчёт второго интеграла — в последней скобке (8-10)^3 должно быть (и, даже, как у вас написано, потом всё равно неверное посчитано). Правильный ответ будет 640/3*pi.

    В идеале, если цель стоит действительно научить, то было бы лучше всего обосновать формулу объема тела вращения. Там реально очень простая идея — тело представляется набором эдаких дисков толщины dx и площадью \pi*f(x)^2, объем одного «блина» будет \pi*f(x)^2*dx. Стопка таких блинов будет приближать объем фигуры, и переходя к пределу нулевой толщины: получаем интеграл и точную формулу объема. Очень наглядная и простая концепция, которая была бы полезной для тех, кто забыл про интеграл.


    1. Enthusiastic_programmer Автор
      28.04.2019 08:57
      #20085630

      Добрый день!

      Формула, о которой вы говорите, проходится в 9 классе школы. Мне кажется немного очевидным объяснять этот материал.

      В данном случае в качестве параметра в интеграле фигурирует точка, где одна кривая переходит в другую. В реальном мире гораздо легче провести измерения всей длины яйца, чем найти эту точку, ведь яйца не представляют собой такой великолепный график, представленный на Рисунке 2.

      Про границы интегралов. Исправил, спасибо за корректировку!

      Расчет оказался неверным, да. Было исправлено.


      1. akhalat
        28.04.2019 09:26
        #20085676

        Вы неправильно «исправили», я же написал как надо и какой должен быть ответ.
        Там будет 1024pi/3, в числах около 51 см^3.

        И зря убрали часть про «эксперимент», там только надо было убрать «точное» число в 47, а написать, что уровень воды между двумя делениями, так что объём где-то около 50. И совпадать неплохо будет

        Общая формула, кстати, будет V=pi*h^3/12 — гораздо проще, чем какие-то коэффициенты подобия и перемасштабирование.

        > В данном случае в качестве параметра в интеграле фигурирует точка, где одна кривая переходит в другую.
        Вообще — нет. Параметр можно произвольно выбирать, они все элементарно связаны. Тем более вы ввели ограничением на параметр тем фактом, что точка перехода должна быть на половине высоты яйца.

        Насчет того, что материал якобы «очевиден» — не соглашусь. Необходимо доказывать изотропоность масштабирования относительно заданного параметра, т.е. иными словами, что во всех трех направлениях растяжение будет одинаковым.

        Кстати, тег «диф. уравнения» у вас лишний. Никаких уравнений вы не решаете и в статье нет ни одного.


        1. Enthusiastic_programmer Автор
          28.04.2019 09:54
          #20085716

          Все учел! Вы вывели очень изящную формулу. Спасибо!


          1. akhalat
            28.04.2019 09:59
            #20085722

            Вы изменили ответ, но не исправили неверный вывод :)
            Пожалуйста, в последней скобке перед "=640pi/3" исправьте (16-8)^3 на (8-10)^3.
            А так — и вам спасибо.


  1. samodum
    27.04.2019 22:56
    #20085228
    +14

    >" многие задаются вопросом: «Какой же объём у куриного яйца»"
    Что?!!! МНОГИЕ?


    1. Vsevo10d
      28.04.2019 00:27
      #20085328
      +2

      Честно говоря, готовя себе и встречая иногда в рецептах «возьмите 1-2 яйца», я задаюсь вопросом, какой же имелся в виду объем.


      1. wtpltd
        28.04.2019 01:19
        #20085380

        Честно говоря, настраивая различный софт и встречая иногда в мануалах «укажите необходимый размер памяти для @#$!@$», я задаюсь вопросом, не то, чтобы что такое "@#$!@$", а хотя бы в каких попугаях этот размер указывать.
        Так что, составители кулинарных рецептов святые люди. Им бы мастерклассы устраивать для мурзилкописателей.


        1. Enthusiastic_programmer Автор
          28.04.2019 08:58
          #20085632
          +1

          Добрый день! Ошибка в преобразовании формул у хабра, посмотрите статью в полной версии.


  1. engine9
    28.04.2019 00:56
    #20085366

    Автор бог заголовка.


    1. Apx
      28.04.2019 01:05
      #20085374
      +1

      Воистину xD


    1. Enthusiastic_programmer Автор
      28.04.2019 09:05
      #20085648

      Это точно не кликбейт!


  1. Daddy_Cool
    28.04.2019 01:24
    #20085386
    +1

    Истинность этого была подтверждена экспериментально

    Вы видимо имели ввиду не «истинность», а э… «с достаточной точностью». Зануда-mode ON.
    Кстати занятно, что яйцо которое линейно больше примерно на четверть (на 26%) имеет в ДВА раза больший объем. Таким образом одна коробка яиц СО тянет на две коробки яиц C3, правда С3 кажется в магазинах не встречаются.


    1. Enthusiastic_programmer Автор
      28.04.2019 09:06
      #20085652

      В следующий раз при покупке яиц вспомню об этом, спасибо!


  1. wormball
    28.04.2019 01:58
    #20085414
    +1

    Измерить 47 мл мензуркой с ценой деления 100 мл — подвиг, достойный Чака Норриса. Хотя лучше было бы, конечно, измерить ровно 47,57142 мл.


    1. Enthusiastic_programmer Автор
      28.04.2019 09:00
      #20085640
      +1

      Добрый день! Я научился проводить эксперименты подобным образом еще на уроках физики. А вы помните школьные годы, когда все не сходилось, но надо было, чтоб сошлось?


  1. wormball
    28.04.2019 02:08
    #20085418
    +3

    > Чем обусловлен такой выбор? Полученная кривая в большей степени напоминает яйцо, чем любая другая кривая, составленная из двух уравнений.

    Это сильно, конечно. Методы аппроксимации уже отменили, видать. Даже просто наложить фотографию яйца на график функции, судя по всему, запрещено. Не говоря уже об том, чтобы поискать в гугле по запросу «формула яйца».


  1. wormball
    28.04.2019 02:39
    #20085430
    +2

    В наибольшей, говорите, степени напоминает яйцо?



    Что-то мне подсказывает, что на самом деле у вашего яйца объём 65 — 67 мл.


    1. Enthusiastic_programmer Автор
      28.04.2019 09:01
      #20085642
      +1

      Ого! Ничего себе, как точно легло! Фантастика!


  1. vortupin
    28.04.2019 05:03
    #20085474

    Истинность этого была подтверждена экспериментально
    Ну, хорошо, что старый анекдот про Эдисона и Эптона вам известен ;)

    Христос воскресе!


    1. Enthusiastic_programmer Автор
      28.04.2019 09:02
      #20085644
      +1

      Воистину воскрес! С праздником Вас!


  1. AllegroMod
    28.04.2019 09:34
    #20085684

    Архимед бы утопился в ванне от таких вычислений