Привет, трудящиеся. Не буду надолго задерживать ваше внимание объяснением декларативного подхода, попробую предложить решить еще одну задачку используя язык логического программирования, как вариант декларативного взгляда на формулировку проблем и их решений.
Задача 391. Perfect Rectangle
Given N axis-aligned rectangles where N > 0, determine if they all together form an exact cover of a rectangular region.
Each rectangle is represented as a bottom-left point and a top-right point. For example, a unit square is represented as [1,1,2,2]. (coordinate of bottom-left point is (1, 1) and top-right point is (2, 2)).
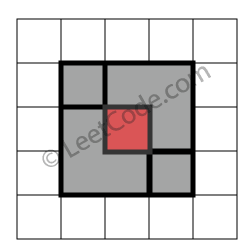
Example 1: rectangles = [
[1,1,3,3],
[3,1,4,2],
[3,2,4,4],
[1,3,2,4],
[2,3,3,4]]
Return true. All 5 rectangles together form an exact cover of a rectangular region.
…
Example 3:rectangles =
[ [1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[3,2,4,4]]
Return false. Because there is a gap in the top center.
В раздумьях над формулировкой проходит второй день, это конечно не недельные занятия над включением винтажных ламп, но все же хочу представить результаты работы над задачей. Понадобилось несколько попыток, чтобы решить все имеющиеся тесты.
Исходные данные представлены списком, напомню коротко, список это — [Голова|Хвост], где Хвост- список, также список бывает пустым [].
Формулируем 1
Нужно подсчитать общую площадь всех прямоугольников, найти максимальный размер описывающего их всех прямоугольника и сверить эти две суммы, если равно значит все прямоугольники накрыли равномерно площадь. В это же время проверим, что прямоугольники не пересекаются, каждый новый прямоугольник будем добавлять в список, он по условию не должен накладываться и пересекать все предыдущие.
Для этого применяю хвостовую рекурсию(она же, рекурсия на спуске), самый "императивный" способ представить цикл. В одном таком "цикле", найдем сразу общую сумму площадей и минимальный левый и максимальный правый угол описывающего прямоугольника, походу, накапливая общий список фигур, проверяя, чтобы не было пересечений.
Вот так:
findsum([], Sres,Sres,LConerRes,LConerRes,RConerRes,RConerRes,_).
findsum([[Lx,Ly,Rx,Ry]|T], Scur,Sres,LConerCur,LConerRes,RConerCur,RConerRes,RectList):-
mincon(Lx:Ly,LConerCur,LConerCur2),
maxcon(Rx:Ry,RConerCur,RConerCur2),
Scur2 is Scur+(Rx-Lx)*(Ry-Ly),
not(chekin([Lx,Ly,Rx,Ry],RectList)),
findsum(T, Scur2,Sres,LConerCur2,LConerRes,RConerCur2,RConerRes,[[Lx,Ly,Rx,Ry]|RectList]).У Пролога переменные — это неизвестные, их нельзя изменить, они или пусты или приняли значение, отсюда требуется пара переменных, начальная и результирующая, когда добираемся до конца списка, текущее значение станет результирующим (первая строка правила). В отличие от императивных языков, для поддержки понимания строки программы надо вообразить весь путь, который к ней привел, и все переменные могут иметь свою "историю" накопления, тут же, каждая строка программы только в контексте текущего правила, всё состояние, которое на нее повлияло налицо вход правила.
Итак:
%самый левый угол
mincon(X1:Y1,X2:Y2,X1:Y1):-X1=<X2,Y1=<Y2,!.
mincon(_,X2:Y2,X2:Y2).
%самый правый
maxcon(X1:Y1,X2:Y2,X1:Y1):-X1>=X2,Y1>=Y2,!.
maxcon(_,X2:Y2,X2:Y2).Тут для представления угла использован "структурированный терм" вида X:Y, это возможность соединить несколько значений в структуру, так сказать кортеж, только функтором может выступать любая операция. А отсечение "!", позволяет во второй строке правила не указывать условие, это способ повысить эффективность вычислений.
И как оказалось далее, самое важно — проверка непересечения прямоугольников, накапливаются они в списке:
%обход всех элементов списка
chekin(X,[R|_]):-cross(X,R),!.
chekin(X,[_|T]):-chekin(X,T).
%пересечение одного с другим или наоборот, или накладываются полностью
cross(X,X):-!.
cross(X,Y):-cross2(X,Y),!.
cross(X,Y):-cross2(Y,X).
%пересекаются, если вершина одного прямоугольника внутри другого
cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11<X22,X22=<X12,Y11<Y22,Y22=<Y12,!.%rt
cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11=<X21,X21<X12,Y11<Y22,Y22=<Y12,!.%lt
cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11<X22,X22=<X12,Y11=<Y21,Y21<Y12,!.%rb
cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11=<X21,X21<X12,Y11=<Y21,Y21<Y12. %lbПересечение прямоугольников, это четыре варианта попадания вершины первого внутрь другого.
И финальное высказывание:
isRectangleCover(Rects):-
[[Lx,Ly,Rx,Ry]|_]=Rects,
findsum(Rects,0,S,Lx:Ly,LconerX:LconerY,Rx:Ry,RconerX:RconerY,[]),!,
S=:= (RconerX-LconerX)*(RconerY-LconerY).На входе список фигур, первую берем для начальных значений левого и правого угла, выполняем обход всех, подсчитав общую площадь, и сверяем полученные суммы. Замечу, если произошло пересечение прямоугольников, то поиск суммы "откажет", вернет "фолс", это значит что и сверять суммы нечего. То же происходит, если во входном списке не будет ни одной фигуры, будет отказ, нечего сверять...
Далее эту реализацию, запускаю на имеющихся тестах, привожу первые 40:
%unit-tests framework
assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec).
assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec).
assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp).
:-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]),true).
:-assert_are_equal(isRectangleCover([[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]),false).
:-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]),false).
:-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[0,0,4,1]]),false).:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[6,2,8,3],[5,1,6,3],[4,0,5,1],[6,0,7,2],[4,2,5,3],[2,1,4,3],[0,1,2,2],[0,2,2,3],[4,1,5,2],[5,0,6,1]]),true).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),true).
:-assert_are_equal(isRectangleCover([[0,0,4,1]]),true).
:-assert_are_equal(isRectangleCover([[0,0,3,3],[1,1,2,2]]),false).
:-assert_are_equal(isRectangleCover([[1,1,2,2],[1,1,2,2],[2,1,3,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,3,2],[1,0,2,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,1,2],[0,2,1,3],[0,3,1,4]]),true).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[1,0,2,1],[2,0,3,1],[3,0,4,1]]),true).
:-assert_are_equal(isRectangleCover([[0,0,2,2],[1,1,3,3],[2,0,3,1],[0,3,3,4]]),false).
:-assert_are_equal(isRectangleCover([[0,0,3,1],[0,1,2,3],[1,0,2,1],[2,2,3,3]]),false).
:-assert_are_equal(isRectangleCover([[1,1,3,3],[2,2,4,4],[4,1,5,4],[1,3,2,4]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,2,1],[1,0,2,1],[0,2,2,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,2,1],[0,1,2,2],[0,2,1,3],[1,0,2,1]]),false).
:-assert_are_equal(isRectangleCover([[1,1,2,2],[0,1,1,2],[1,0,2,1],[0,2,3,3],[2,0,3,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[6,2,8,3],[5,1,6,3],[6,0,7,2],[4,2,5,3],[2,1,4,3],[0,1,2,2],[0,2,2,3],[4,1,5,2],[5,0,6,1]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,4],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,3],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,5,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[0,2,1,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,3,3],[1,1,2,2],[1,1,2,2]]),false).
:-assert_are_equal(isRectangleCover([[1,1,4,4],[1,3,4,5],[1,6,4,7]]),false).
:-assert_are_equal(isRectangleCover([[0,0,3,1],[0,1,2,3],[2,0,3,1],[2,2,3,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[1,1,2,2],[1,1,2,2]]),false).
:-assert_are_equal(isRectangleCover([[1,1,2,2],[1,1,2,2],[1,1,2,2],[2,1,3,2],[2,2,3,3]]),false).
:-assert_are_equal(isRectangleCover([[1,1,2,2],[2,1,3,2],[2,1,3,2],[2,1,3,2],[3,1,4,2]]),false).
:-assert_are_equal(isRectangleCover([[0,1,2,3],[0,1,1,2],[2,2,3,3],[1,0,3,1],[2,0,3,1]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,2,1,3],[1,1,2,2],[2,0,3,1],[2,2,3,3],[1,0,2,3],[0,1,3,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[2,2,3,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,1,2],[0,2,1,3],[1,0,2,1],[1,0,2,1],[1,2,2,3],[2,0,3,1],[2,1,3,2],[2,2,3,3]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1]]),false).
:-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[-1,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false).
:-assert_are_equal(isRectangleCover([[0,0,1,1],[1,0,2,1],[1,0,3,1],[3,0,4,1]]),false).
:-assert_are_equal(isRectangleCover([[1,2,4,4],[1,0,4,1],[0,2,1,3],[0,1,3,2],[3,1,4,2],[0,3,1,4],[0,0,1,1]]),true).И это еще не конец, задача из раздела "хард", в 41 тесте предлагают список из 10000 прямоугольников, во всех последних пяти тестах получаю такие времена в секундах:
test 41:length=10000
goal->ok:212/sec
test 42:length=3982
goal->ok:21/sec
test 43:length=10222
goal->ok:146/sec
test 44:length=10779
goal->ok:41/sec
test 45:length=11000
goal->ok:199/secПривести входящие значения не могу, в редактор они не помещаются, прикреплю вот так тест 41.
Формулировка 2
Предыдущий подход, использовать список для накопления фигур, оказывается сильно неэффективным, какое напрашивается изменение — вместо сложности n^2 сделать n*log(n). Для проверки пересечений списка прямоугольников можно использовать дерево.
Бинарное дерево для Пролога, это также структурированный терм, и как список он рекурсивно определен, дерево оно пустое или содержит значение и два поддерева.
Использую для этого трехместный функтор: t(LeftTree, RootValue, RightTree), а пустое дерево будет [].
Простое дерево из чисел, с упорядочением слева меньшие, а справа большие, можно выразить вот так:
add_to_tree(X,[],t([],X,[])).
add_to_tree(X,t(L,Root,R),t(L,Root,NewR)):- X<Root,!,add_to_tree(X,R,NewR).
add_to_tree(X,t(L,Root,R),t(NewL,Root,R)):- add_to_tree(X,L,NewL).В классической книге И.Братко "Программирование на языке Пролог для искусственного интеллекта" приведено множество реализаций деревьев 2-3, сбалансированные АВЛ…
Вопрос упорядочения прямоугольников предлагаю решать так: если прямоугольник находиться правее другого, то они не пересекаются, а те что левее надо проверять на пересечение. А правее, это когда правый угол одного меньше левого угла второго:
righter([X1,_,_,_],[_,_,X2,_]):-X1>X2.И задача накопления фигур в дерево, плюс проверка на пересечение может выглядеть вот так, когда новый прямоугольник правее находящегося в корне, тогда проверять надо справа иначе проверять пересечения слева:
treechk(X,[],t([],X,[])).
treechk([X1,Y1,X2,Y2],t(L,[X1,Y11,X2,Y22],R),t(L,[X1,Yr,X2,Yr2],R)):- (Y1=Y22;Y2=Y11),!,Yr is min(Y1,Y11),Yr2 is max(Y2,Y22). %union
treechk(X,t(L,Root,R),t(L,Root,NewR)):- righter(X,Root),!,treechk(X,R,NewR).
treechk(X,t(L,Root,R),t(NewL,Root,R)):- not(cross(X,Root)),treechk(X,L,NewL).Тут же учтена еще одну хитрость особенность, если прямоугольники совпадают по ширине, и имеют общую грань, то их можно объединить в один и не добавлять в дерево, а просто изменить в одном узле размер прямоугольника. К этому подталкивает тест 41, там такого вида данные: [[0,-1,1,0],[0,0,1,1],[0,1,1,2],[0,2,1,3],[0,3,1,4],[0,4,1,5],[0,5,1,6],[0,6,1,7],[0,7,1,8],[0,8,1,9],[0,9,1,10],[0,10,1,11],[0,11,1,12],[0,12,1,13],[0,13,1,14],...,[0,9998,1,9999]].
Эти усовершенствования соединим с предыдущим решением, привожу полностью, с некоторыми улучшениями:
treechk(X,[],t([],X,[])).
treechk([X1,Y1,X2,Y2],t(L,[X1,Y11,X2,Y22],R),t(L,[X1,Yr,X2,Yr2],R)):- (Y1=Y22;Y2=Y11),!,Yr is min(Y1,Y11),Yr2 is max(Y2,Y22). %union
treechk(X,t(L,Root,R),t(L,Root,NewR)):- righter(X,Root),!,treechk(X,R,NewR).
treechk(X,t(L,Root,R),t(NewL,Root,R)):- not(cross(X,Root)),treechk(X,L,NewL).
righter([X1,_,_,_],[_,_,X2,_]):-X1>X2.
findsum([],Sres,Sres,LConerRes,LConerRes,RConerRes,RConerRes,_).
findsum([[Lx,Ly,Rx,Ry]|T],Scur,Sres,LConerCur,LConerRes,RConerCur,RConerRes,RectTree):-
coner(Lx:Ly,LConerCur,=<,LConerCur2),
coner(Rx:Ry,RConerCur,>=,RConerCur2),
Scur2 is Scur+abs(Rx-Lx)*abs(Ry-Ly),
treechk([Lx,Ly,Rx,Ry],RectTree,RectTree2),!,
findsum(T,Scur2,Sres,LConerCur2,LConerRes,RConerCur2,RConerRes,RectTree2).
isRectangleCover(Rects):-
[[Lx,Ly,Rx,Ry]|_]=Rects,
findsum(Rects,0,S,Lx:Ly,LconerX:LconerY,Rx:Ry,RconerX:RconerY,[]),!,
S=:= abs(RconerX-LconerX)*abs(RconerY-LconerY).
coner(X1:Y1,X2:Y2,Dir,X1:Y1):-apply(Dir,[X1,X2]),apply(Dir,[Y1,Y2]),!.
coner(_,XY,_,XY).
cross(X,X):-!.
cross(X,Y):-cross2(X,Y),!.
cross(X,Y):-cross2(Y,X).
cross2([X11,Y11,X12,Y12],[_,_,X22,Y22]):-X11<X22,X22=<X12, Y11<Y22,Y22=<Y12,!. %right-top
cross2([X11,Y11,X12,Y12],[X21,_,_,Y22]):-X11=<X21,X21<X12, Y11<Y22,Y22=<Y12,!. %left-top
cross2([X11,Y11,X12,Y12],[_,Y21,X22,_]):-X11<X22,X22=<X12, Y11=<Y21,Y21<Y12,!. %right-bottom
cross2([X11,Y11,X12,Y12],[X21,Y21,_,_]):-X11=<X21,X21<X12, Y11=<Y21,Y21<Y12. %left-bottomВот такое время выполнения "тяжелых" тестов:
goal-true->ok:0/sec
41:length=10000
goal-true->ok:0/sec
42:length=3982
goal-true->ok:0/sec
43:length=10222
goal-true->ok:2/sec
44:length=10779
goal-false->ok:1/sec
45:length=11000
goal-true->ok:1/secНа этом совершенствования закончу, все тесты проходят верно, время удовлетворительное. Кто заинтересовался, предлагаю попробовать онлайн или тут.
Итого
Статьи связанные с функциональным программированием, с постоянной частотой встречаются на портале. Я затрагиваю, еще один аспект декларативного подхода — логическое программирование. Можно представлять задачи с помощью логического описания, есть факты и правила, посылки и следствия, отношения и рекурсивные отношения. Описание задачи нужно превратить в набор отношений ее описывающих. Результат — это следствие разложения проблемы на более простые составляющие.
Программой на декларативном языке, можно пользоваться как набором высказываний, которые должны сконструировать результат, решение задачи в ее удачной формулировке. А оптимизация может состоять, например, в том, что "беглое" описание способа контроля пересечений прямоугольников, может потребовать уточнения, доступно сконструировать древовидную структуру, для более эффективных вычислений.
И… куда-то пропал Prolog из стилей исходного кода, еще полгода назад я им пользовался. Пришлось указывать "родственный" Erlang. А не похоже ли это на "популярность", в списке нет и Фортрана с Бейсиком, что это рейтинг языков?
Комментарии (8)

nickolaym
05.05.2019 01:02+1Это не "просто о прологе".
Это навалить кучу кода без комментариев и пробелов, нате, читайте! Пробелы-то чем провинились?
Что этот код должен был проиллюстрировать?
Тяп-ляп-реализацию какого-то дерева? "Смотрите, как можно быстро фигачить на прологе"?
Ни то, как декомпозировать задачу для выражения на прологе.
Ни особенности его вычислительной модели. Только коротко "переменные бывают или пустые, или связанные", и "отсечка повышает эффективность вычислений".
То, что у пролога список доступен для прямого паттерн-матчинга, сподвигает к плохим — с соображений ФП — практикам каждый раз писать операции обработки списков в виде явных циклов (ну хорошо, хорошо, рекурсий).
Как насчёт переписать всё это с использованием fold? Не станет более читаемо?
Одно из достоинств пролога (и его же беда) — то, что можно как проверять гипотезы, так и из любого набора входных аргументов пытаться доукомплектовать непротиворечивый набор оставшихся. То есть, нет в чистом виде деления на in- и out-параметры.
Если мы эмулируем ФП с монадой Maybe, подразумевая, что "вот это у нас входы, вот это у нас выходы", — то будет один стиль программирования. Если пишем биекцию f(X,Y) как функции X(Y) и Y(X), то совсем другой, учитывающий, например, что там, где в одном направлении происходит свёртка, в другом будет развёртка списка, к примеру. И потребуется пропетлять между всякими зацикливаниями. И смысл отсечек разный.
Если уж так разобраться, то декларативность пролога начинается и заканчивается декларациями о добрых намерениях.
Как только мы начинаем размышлять "как вычислить ту или иную функцию (предикат? я сказал "предикат"? нет, именно "функцию"), становится ясно, что порядок перебора ветвей важен, а значит, здравствуй, императивность.
Завёрнутая в чистые функции над иммутабельными переменными. Завёрнутыми в предикаты, порождающие семейства функций. Причём в этих семействах мы ещё должны пометить себе на бумажке, в комментариях, в ассертах, — какие члены этих семейств имеют право на существование, а какие нет.
Но это будет — непросто о прологе.

go-prolog Автор
05.05.2019 02:13Да, спасибо за отзыв,
это просто пример представления задач на Прологе. Эти "тяп-ляп" дают решение, достаточно эффективное.
Это навалить кучу кода без комментариев и пробелов, нате, читайте!
Тут же не очередной "туториал" для обучения — это иллюстрация, задачу можно представить логическим представлением и да, довольно быстро. Перед каждым правилом было объяснение, а отсутствие пробелов, только в пределах строки, по моему читабельно.
На "свертку" действительно похоже, ее можно реализовать как мета-предикат, а используют в основном findall(), setof()…
И про разделение входных и выходных параметров интерестно, меня как раз "забавляет" возможность описать конкатенацию, а применять ее как деление, это же возможности унификации, а не просто паттерн-метчинг, это описание отношений между параметрами правила:
append([],X,X). append([H|T],X,[H|Y]):-append(T,X,Y). ?>append(X,Y,[a,b,c]).
такое приведет к разделению списка, это именно
иммутабельные переменныенеизвестные X,Y значения которых нужно установить.
Эрланг (который приходиться использовать для оформления кода), имея похожую запись, не приводит к такому эффекту, все же разные основы:
append([],X)->X; append([H|T],X)->[H|append(T,X)].
nickolaym
05.05.2019 14:28Поскольку за декларативностью всё равно прячется императивность, — то оказывается важно, в каком порядке будут перебраны варианты, отвечающие предикату.
Разбиение списка [x0,x1,...,xn] может давать перебор с головы или с хвоста:
[]+[x0,x1,...,xn], [x0]+[x1,...,xn], ..., [x0,x1,...,xn]+[]
соответственно, код будет разный — смотря чего хотелось.
Банально, от перестановки веток зависит
% чуть эффективнее, если первый список пустой cat1([],Ys,Ys). cat1([X1|Xs],Ys,[X1|XYs]) :- cat1(Xs,Ys,XYs). % эффективнее для непустых первых списков (вторая ветка матчится единожды) cat2([X1|Xs],Ys,[X1|XYs]) :- cat2(Xs,Ys,XYs). cat2([],Ys,Ys). % типа, балансируем нагрузку! cat3a([],Ys,Ys). cat3a([X1|Xs],Ys,[X1|XYs]) :- cat3b(Xs,Ys,XYs). cat3b([X1|Xs],Ys,[X1|XYs]) :- cat3a(Xs,Ys,XYs). cat3b([],Ys,Ys).
Криво (непродуманно) (недодуманно) (не предназначенно для неправильных сочетаний in/out-параметров) написанный код легко можно вогнать в рекурсию.
Например,cat(_,[1,2,3],Zs)— то есть, "список, хвостом которого является [1,2,3]".
В случае с cat1 он даст Zs = [1,2,3], [_a,1,2,3], [_a,_b,1,2,3] и т.д.
В случае с cat2 — уйдёт в бесконечность.
Тут даже отсечки не помогут...
go-prolog Автор
05.05.2019 19:18Соглашусь и отношусь к этому как к особенности, которая ограничивает, но все равно механизмы интересные.
Мне нравится пример с натуральными числами, вот так их можно представить:
natural(0). natural(X+1):-natural(X).
Тогда сумма двух чисел, она же разность:
nsumma(0,X,X). nsumma(X+1,Y,Z+1) :- nsumma(X,Y,Z).
Произведение выглядит вот так:
nmult(0,_,0). nmult(X+1,Y,Z) :- nmult(X,Y,Z1), nsumma(Y,Z1,Z).
С помощью него выполнить деления не получается, такая цель зацикливается:
?- nmult(X,Y,0+1+1+1+1+1+1). X = 0+1, Y = 0+1+1+1+1+1+1 ; X = 0+1+1, Y = 0+1+1+1 ; ERROR: Out of global-stack.
Но добавим ограничения, типа, все числа в заданном диапазоне, можно вот так:
tonatural(0,0). tonatural(N,X+1) :- N>0, N1 is N-1, tonatural(N1,X). nrange(A,B,N):-A<B, tonatural(A,N). nrange(A,B,N):-A<B, A1 is A+1, nrange(A1,B,N).
И умножение будет разложением на множители, где неизвестные лежат в указанном диапазоне :
?- nrange(0,10,X), nrange(0,10,Y), nmult(X,Y,0+1+1+1+1+1+1). X = 0+1, Y = 0+1+1+1+1+1+1 ; X = 0+1+1, Y = 0+1+1+1 ; X = 0+1+1+1, Y = 0+1+1 ; X = 0+1+1+1+1+1+1, Y = 0+1 ;

Tzimie
05.05.2019 20:04Было.бы интересно, схавает ли пролог laver tables: https://en.m.wikipedia.org/wiki/Laver_table
Определены они элементарно, всего двумя условиями, но нетривиально, как бы с конца.
Кроме того, с этими таблицами связана магия (rank into rank)

go-prolog Автор
06.05.2019 23:26Интересно,
если посчитать и посмотреть, то вот так:
swish.swi-prolog.org/p/Laver%20table.pl


Tzimie
Меня всегда интересовало, как это работает на реальных, а не игрушечных примерах в NP полных задачах, где единственный выход — задавать эвристики? Как они задаются? Как отслеживать прогресс поиска когда он думает час, другой, и непонятно,, сколько осталось, пара минут или миллиард лет
go-prolog Автор
В целом это ,, иной,, способ декомпозиции задач. ограничения, эвристики доступны как и везде. Доступна отладка есть профилиррвщик, да и отладочные печати, логирование реализовать нет проблем…