Ошибки и ПО шли рука об руку с самого начала эпохи программирования компьютеров. Со временем разработчики выработали набор практик по тестированию и отладке программ до их развёртывания, однако эти практики уже не подходят к современным системам с глубоким обучением. Сегодня основной практикой в области машинного обучения можно назвать тренировку на определённом наборе данных с последующей проверкой на другом наборе. Таким способом можно подсчитать среднюю эффективность работы моделей, однако важно также гарантировать надёжность, то есть приемлемую эффективность в худшем случае. В данной статье мы опишем три подхода для точного определения и устранения ошибок в обученных прогнозирующих моделях: состязательное тестирование [adversarial testing], устойчивое обучение [robust learning] и формальную верификацию [formal verification].
Системы с МО по определению не устойчивы. Даже системы, выигрывающие у человека в определённой области, могут не справиться с решением простых задач при внесении малозаметных различий. К примеру, рассмотрим проблему внесения возмущений в изображения: нейросеть, способную классифицировать изображения лучше людей, легко заставить поверить в то, что ленивец – это гоночный автомобиль, добавив небольшую долю тщательно рассчитанного шума в изображение.

Состязательные входные данные при наложении на обычное изображение могут сбить ИИ с толку. Два крайних изображения отличаются не более, чем на 0,0078 для каждого пикселя. Первое классифицируется, как ленивец, с 99% вероятностью. Второе – как гоночный автомобиль с 99% вероятностью.
Эта проблема не нова. У программ всегда были ошибки. Десятилетия программисты набирали впечатляющий набор техник, от модульного тестирования до формальной верификации. На традиционных программах эти методы работают хорошо, но адаптировать эти подходы для тщательного тестирования МО-моделей чрезвычайно сложно из-за масштаба и отсутствия структуры в моделях, способных содержать сотни миллионов параметров. Это говорит о необходимости разработки новых подходов для обеспечения надёжности МО-систем.
С точки зрения программиста, баг – это любое поведение, не соответствующее спецификации, то есть, запланированной функциональности системы. В рамках наших исследований ИИ мы проводим изучение техник оценки того, соответствуют ли МО-системы требованиям не только на тренировочном и тестовом наборе, но и списку спецификаций, описывающих желаемые свойства системы. Среди таких свойств может быть устойчивость к достаточно малым изменениям входных данных, ограничения по безопасности, предотвращающие катастрофические отказы, или соответствие предсказаний законам физики.
В данной статье мы обсудим три важных технических проблемы, с которыми сообщество МО сталкивается, работая с целью сделать МО-системы устойчивыми и надёжно соответствующими желаемым спецификациям:
Устойчивость к состязательным примерам – достаточно неплохо изученная проблема ГО. Один из главных сделанных выводов – важность оценки действий сети в результате сильных атак, и разработка прозрачных моделей, которые можно анализировать достаточно эффективно. Мы, вместе с другими исследователями, обнаружили, что многие модели оказываются устойчивыми против слабых состязательных примеров. Однако они дают практически 0% точность для более сильных состязательных примеров (Athalye et al., 2018, Uesato et al., 2018, Carlini and Wagner, 2017).
Хотя большая часть работы концентрируется на редких отказах в контексте обучения с учителем (и в основном это классификация изображений), есть необходимость расширять применение этих идей и на другие области. В недавней работе с состязательным подходом к поиску катастрофических отказов, мы применяем эти идеи к тестированию сетей, обученных с подкреплением, и предназначенных для использования в местах с высокими требованиями к безопасности. Одна из проблем разработки автономных систем состоит в том, что, так как у одной ошибки могут быть серьёзные последствия, даже небольшая вероятность отказа не считается приемлемой.
Наша цель – спроектировать «соперника», который поможет распознать подобные ошибки заранее (в контролируемом окружении). Если соперник сможет эффективно определить наихудшие входные данные для заданной модели, это позволит нам отловить редкие случаи отказов до её развёртывания. Как и в случае с классификаторами изображений, оценка работы со слабым соперником даёт ложное чувство безопасности во время развёртывания. Этот подход похож на разработку ПО при помощи «красной команды» [red-teaming – привлечение сторонней команды разработчиков, принимающих на себя роль злоумышленников с целью обнаружения уязвимостей / прим. перев.], однако выходит за рамки поиска отказов, вызванных злоумышленниками, а также включает в себя ошибки, проявляющиеся естественным образом, к примеру, из-за недостаточной генерализации.
Мы разработали два взаимодополняющих подхода к состязательному тестированию сетей, обучаемых с подкреплением. В первом мы используем оптимизацию без деривативов, чтобы напрямую минимизировать ожидаемую награду. Во втором мы узнаём функцию состязательного значения, на опыте предсказывающую, в каких ситуациях сеть может отказать. Затем мы используем эту выученную функцию для оптимизации, концентрируясь на оценке наиболее проблемных входных данных. Эти подходы формируют лишь небольшую часть богатого и растущего пространства потенциальных алгоритмов, и нам очень интересно будущее развития этой области.
Оба подхода уже демонстрируют значительные улучшения по сравнению со случайным тестированием. Используя наш метод, можно за несколько минут обнаружить недостатки, которые раньше приходилось бы искать целыми днями, а возможно, и вообще нельзя было найти (Uesato et al., 2018b). Мы также обнаружили, что состязательное тестирование может вскрыть качественно иное поведение сетей по сравнению с тем, что можно было бы ожидать от оценки на случайном тестовом наборе. В частности, используя наш метод, мы обнаружили, что сети, выполнявшие задачу ориентирования на трёхмерной карте, и обычно справляющиеся с этим на уровне человека, не могут найти цель в неожиданно простых лабиринтах (Ruderman et al., 2018). Наша работа также подчёркивает необходимость проектирования систем, безопасных по отношению к естественным отказам, а не только к соперникам.

Проводя тесты на случайных выборках, мы практически не встречаем карт с высокой вероятностью отказа, но состязательное тестирование показывает существование таких карт. Вероятность отказа остаётся большой даже после удаления многих стен, то есть упрощения карт по сравнению с оригинальными.
Состязательное тестирование пытается найти контрпример, нарушающий спецификации. Часто оно переоценивает согласованность моделей этим спецификациям. С математической точки зрения, спецификация – это некое взаимоотношение, которое должно сохраняться между входными и выходными данными сети. Оно может принять форму верхней и нижней границы или неких ключевых параметров ввода и вывода.
Вдохновляясь этим наблюдением, несколько исследователей (Raghunathan et al., 2018; Wong et al., 2018; Mirman et al., 2018; Wang et al., 2018), включая и нашу команду из DeepMind (Dvijotham et al., 2018; Gowal et al., 2018), работали над алгоритмами, инвариантными к состязательному тестированию. Это можно описать геометрически – мы можем ограничить (Ehlers 2017, Katz et al. 2017, Mirman et al., 2018) самое худшее нарушение спецификации, ограничивая пространство выходных данных на основе набора входных. Если эта граница дифференцируема по параметрам сети и её можно быстро вычислить, её можно использовать во время обучения. Затем изначальная граница может распространяться через каждый слой сети.
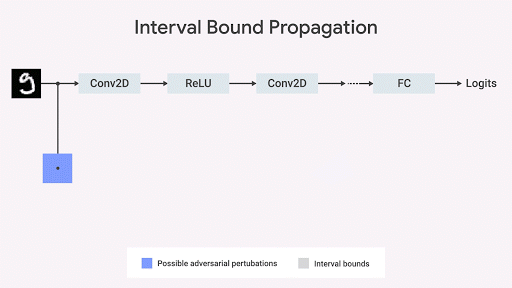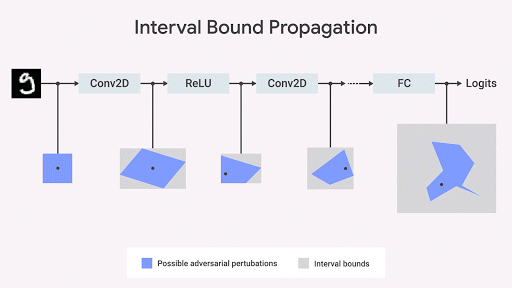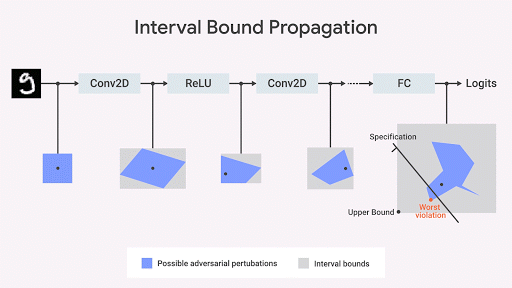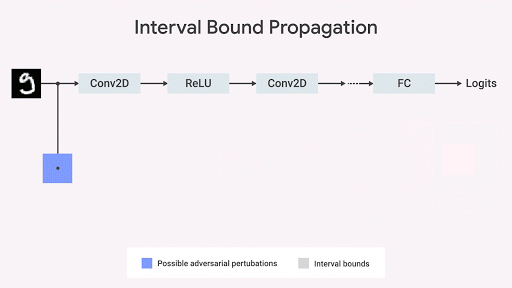
Мы показываем, что распространение границы интервала идёт быстро, эффективно, и – в отличие от того, как считалось ранее – даёт хорошие результаты (Gowal et al., 2018). В частности мы показываем, что оно может доказываемым образом уменьшить количество ошибок (т.е. максимальное количество ошибок, которое может вызвать любой соперник) по сравнению с самыми продвинутыми классификаторами изображений на наборах из баз данных MNIST и CIFAR-10.
Следующей целью будет изучение правильных геометрических абстракций для вычисления чрезмерных аппроксимаций пространства выходных данных. Мы также хотим обучать сети так, чтобы они надёжно работали с более сложными спецификациями, описывающими желаемое поведение, как, например, упомянутые ранее инвариантность и соответствие физическим законам.
Тщательное тестирование и обучение может оказать заметную помощь в создании надёжных систем МО. Однако формально сколь угодно объёмное тестирование не может гарантировать того, что поведение системы совпадёт с нашими желаниями. В крупномасштабных моделях перебор всех возможных вариантов выходных данных для заданного набора входных (к примеру, незначительных изменений изображения) представляется трудно реализуемым делом ввиду астрономического количества возможных изменений изображения. Однако, как и в случае с обучением, можно найти более эффективные подходы к установке геометрических ограничений на множество выходных данных. Формальная верификация является темой текущих исследований, проводимых в DeepMind.
МО-сообщество разработало несколько интересных идей вычисления точных геометрических границ пространства выходных данных сети (Katz et al. 2017, Weng et al., 2018; Singh et al., 2018). Наш подход (Dvijotham et al., 2018), основанный на оптимизации и дуальности, состоит из формулирования задачи верификации в терминах оптимизации, которая пытается найти крупнейшее нарушение проверяемого свойства. Задача становится вычислимой, если использовать идеи из дуальности в оптимизации. В итоге получаем дополнительные ограничения, уточняющие границы, вычисленные при перемещении границы интервала [interval bound propagation] с использованием так называемых отсекающих плоскостей [cutting planes]. Это надёжный, но неполный подход: могут быть случаи, когда интересующее нас свойство выполняется, но вычисленная по этому алгоритму граница оказывается недостаточно строгой, чтобы наличие этого свойства можно было формально доказать. Однако получив границу, мы получаем формальную гарантию отсутствия нарушений данного свойства. На рис. ниже этот подход проиллюстрирован графически.

Этот подход позволяет нам расширить применимость алгоритмов верификации на сети более общего назначения (активаторные функции, архитектуры), общие спецификации и более сложные модели ГО (генеративные модели, нейронные процессы, и т.п.) и спецификации, выходящие за пределы состязательной надёжности (Qin, 2018).
У развёртывания МО в ситуациях с высоким риском есть свои уникальные вызовы и трудности, и для этого требуется разработка технологий оценки, гарантированно обнаруживающих маловероятные ошибки. Мы считаем, что последовательное обучение по спецификациям может значительно улучшить эффективность работы по сравнению с теми случаями, когда спецификации возникают неявно из тренировочных данных. Мы с нетерпением ожидаем результатов текущих исследований состязательной оценки, надёжных моделей обучения и верификации формальных спецификаций.
Потребуется ещё много работы для того, чтобы мы смогли создавать автоматизированные инструменты, гарантирующие, что системы ИИ в реальном мире будут всё «делать правильно». В частности мы очень рады прогрессу в следующих направлениях:
DeepMind настроена на положительное влияние на социум путём ответственной разработки и развёртывания МО-систем. Чтобы убедиться, что вклад разработчиков будет гарантированно положительным, нам нужно справиться со множеством технических препятствий. Мы намерены сделать свой вклад в эту область и с удовольствием работаем с сообществом над решением этих проблем.
Системы с МО по определению не устойчивы. Даже системы, выигрывающие у человека в определённой области, могут не справиться с решением простых задач при внесении малозаметных различий. К примеру, рассмотрим проблему внесения возмущений в изображения: нейросеть, способную классифицировать изображения лучше людей, легко заставить поверить в то, что ленивец – это гоночный автомобиль, добавив небольшую долю тщательно рассчитанного шума в изображение.

Состязательные входные данные при наложении на обычное изображение могут сбить ИИ с толку. Два крайних изображения отличаются не более, чем на 0,0078 для каждого пикселя. Первое классифицируется, как ленивец, с 99% вероятностью. Второе – как гоночный автомобиль с 99% вероятностью.
Эта проблема не нова. У программ всегда были ошибки. Десятилетия программисты набирали впечатляющий набор техник, от модульного тестирования до формальной верификации. На традиционных программах эти методы работают хорошо, но адаптировать эти подходы для тщательного тестирования МО-моделей чрезвычайно сложно из-за масштаба и отсутствия структуры в моделях, способных содержать сотни миллионов параметров. Это говорит о необходимости разработки новых подходов для обеспечения надёжности МО-систем.
С точки зрения программиста, баг – это любое поведение, не соответствующее спецификации, то есть, запланированной функциональности системы. В рамках наших исследований ИИ мы проводим изучение техник оценки того, соответствуют ли МО-системы требованиям не только на тренировочном и тестовом наборе, но и списку спецификаций, описывающих желаемые свойства системы. Среди таких свойств может быть устойчивость к достаточно малым изменениям входных данных, ограничения по безопасности, предотвращающие катастрофические отказы, или соответствие предсказаний законам физики.
В данной статье мы обсудим три важных технических проблемы, с которыми сообщество МО сталкивается, работая с целью сделать МО-системы устойчивыми и надёжно соответствующими желаемым спецификациям:
- Эффективная проверка соответствия спецификациям. Мы изучаем эффективные способы проверки того, что МО-системы соответствуют своим свойствам (к примеру, таким, как устойчивость и инвариантность), которые требуют от них разработчик и пользователи. Один из подходов поиска случаев, в которых модель может отойти от этих свойств – систематический поиск наихудших результатов работы.
- Обучение МО-моделей соответствию спецификациям. Даже при наличии достаточно большого объёма обучающих данных стандартные МО-алгоритмы могут выдавать предсказательные модели, работа которых не соответствует желаемым спецификациям. От нас требуется пересмотреть алгоритмы обучения так, чтобы они не только хорошо работали на тренировочных данных, но и соответствовали желаемым спецификациям.
- Формальное доказательство соответствия МО-моделей желаемым спецификациям. Необходимо разработать алгоритмы, подтверждающие соответствие модели желаемым спецификациям для всех возможных входных данных. Хотя область формальной верификации изучала подобные алгоритмы уже несколько десятилетий, несмотря на её впечатляющий прогресс, эти подходы нелегко масштабировать на современные МО-системы.
Проверка на соответствие модели желаемым спецификациям
Устойчивость к состязательным примерам – достаточно неплохо изученная проблема ГО. Один из главных сделанных выводов – важность оценки действий сети в результате сильных атак, и разработка прозрачных моделей, которые можно анализировать достаточно эффективно. Мы, вместе с другими исследователями, обнаружили, что многие модели оказываются устойчивыми против слабых состязательных примеров. Однако они дают практически 0% точность для более сильных состязательных примеров (Athalye et al., 2018, Uesato et al., 2018, Carlini and Wagner, 2017).
Хотя большая часть работы концентрируется на редких отказах в контексте обучения с учителем (и в основном это классификация изображений), есть необходимость расширять применение этих идей и на другие области. В недавней работе с состязательным подходом к поиску катастрофических отказов, мы применяем эти идеи к тестированию сетей, обученных с подкреплением, и предназначенных для использования в местах с высокими требованиями к безопасности. Одна из проблем разработки автономных систем состоит в том, что, так как у одной ошибки могут быть серьёзные последствия, даже небольшая вероятность отказа не считается приемлемой.
Наша цель – спроектировать «соперника», который поможет распознать подобные ошибки заранее (в контролируемом окружении). Если соперник сможет эффективно определить наихудшие входные данные для заданной модели, это позволит нам отловить редкие случаи отказов до её развёртывания. Как и в случае с классификаторами изображений, оценка работы со слабым соперником даёт ложное чувство безопасности во время развёртывания. Этот подход похож на разработку ПО при помощи «красной команды» [red-teaming – привлечение сторонней команды разработчиков, принимающих на себя роль злоумышленников с целью обнаружения уязвимостей / прим. перев.], однако выходит за рамки поиска отказов, вызванных злоумышленниками, а также включает в себя ошибки, проявляющиеся естественным образом, к примеру, из-за недостаточной генерализации.
Мы разработали два взаимодополняющих подхода к состязательному тестированию сетей, обучаемых с подкреплением. В первом мы используем оптимизацию без деривативов, чтобы напрямую минимизировать ожидаемую награду. Во втором мы узнаём функцию состязательного значения, на опыте предсказывающую, в каких ситуациях сеть может отказать. Затем мы используем эту выученную функцию для оптимизации, концентрируясь на оценке наиболее проблемных входных данных. Эти подходы формируют лишь небольшую часть богатого и растущего пространства потенциальных алгоритмов, и нам очень интересно будущее развития этой области.
Оба подхода уже демонстрируют значительные улучшения по сравнению со случайным тестированием. Используя наш метод, можно за несколько минут обнаружить недостатки, которые раньше приходилось бы искать целыми днями, а возможно, и вообще нельзя было найти (Uesato et al., 2018b). Мы также обнаружили, что состязательное тестирование может вскрыть качественно иное поведение сетей по сравнению с тем, что можно было бы ожидать от оценки на случайном тестовом наборе. В частности, используя наш метод, мы обнаружили, что сети, выполнявшие задачу ориентирования на трёхмерной карте, и обычно справляющиеся с этим на уровне человека, не могут найти цель в неожиданно простых лабиринтах (Ruderman et al., 2018). Наша работа также подчёркивает необходимость проектирования систем, безопасных по отношению к естественным отказам, а не только к соперникам.

Проводя тесты на случайных выборках, мы практически не встречаем карт с высокой вероятностью отказа, но состязательное тестирование показывает существование таких карт. Вероятность отказа остаётся большой даже после удаления многих стен, то есть упрощения карт по сравнению с оригинальными.
Обучение моделей, придерживающихся спецификации
Состязательное тестирование пытается найти контрпример, нарушающий спецификации. Часто оно переоценивает согласованность моделей этим спецификациям. С математической точки зрения, спецификация – это некое взаимоотношение, которое должно сохраняться между входными и выходными данными сети. Оно может принять форму верхней и нижней границы или неких ключевых параметров ввода и вывода.
Вдохновляясь этим наблюдением, несколько исследователей (Raghunathan et al., 2018; Wong et al., 2018; Mirman et al., 2018; Wang et al., 2018), включая и нашу команду из DeepMind (Dvijotham et al., 2018; Gowal et al., 2018), работали над алгоритмами, инвариантными к состязательному тестированию. Это можно описать геометрически – мы можем ограничить (Ehlers 2017, Katz et al. 2017, Mirman et al., 2018) самое худшее нарушение спецификации, ограничивая пространство выходных данных на основе набора входных. Если эта граница дифференцируема по параметрам сети и её можно быстро вычислить, её можно использовать во время обучения. Затем изначальная граница может распространяться через каждый слой сети.

Мы показываем, что распространение границы интервала идёт быстро, эффективно, и – в отличие от того, как считалось ранее – даёт хорошие результаты (Gowal et al., 2018). В частности мы показываем, что оно может доказываемым образом уменьшить количество ошибок (т.е. максимальное количество ошибок, которое может вызвать любой соперник) по сравнению с самыми продвинутыми классификаторами изображений на наборах из баз данных MNIST и CIFAR-10.
Следующей целью будет изучение правильных геометрических абстракций для вычисления чрезмерных аппроксимаций пространства выходных данных. Мы также хотим обучать сети так, чтобы они надёжно работали с более сложными спецификациями, описывающими желаемое поведение, как, например, упомянутые ранее инвариантность и соответствие физическим законам.
Формальная верификация
Тщательное тестирование и обучение может оказать заметную помощь в создании надёжных систем МО. Однако формально сколь угодно объёмное тестирование не может гарантировать того, что поведение системы совпадёт с нашими желаниями. В крупномасштабных моделях перебор всех возможных вариантов выходных данных для заданного набора входных (к примеру, незначительных изменений изображения) представляется трудно реализуемым делом ввиду астрономического количества возможных изменений изображения. Однако, как и в случае с обучением, можно найти более эффективные подходы к установке геометрических ограничений на множество выходных данных. Формальная верификация является темой текущих исследований, проводимых в DeepMind.
МО-сообщество разработало несколько интересных идей вычисления точных геометрических границ пространства выходных данных сети (Katz et al. 2017, Weng et al., 2018; Singh et al., 2018). Наш подход (Dvijotham et al., 2018), основанный на оптимизации и дуальности, состоит из формулирования задачи верификации в терминах оптимизации, которая пытается найти крупнейшее нарушение проверяемого свойства. Задача становится вычислимой, если использовать идеи из дуальности в оптимизации. В итоге получаем дополнительные ограничения, уточняющие границы, вычисленные при перемещении границы интервала [interval bound propagation] с использованием так называемых отсекающих плоскостей [cutting planes]. Это надёжный, но неполный подход: могут быть случаи, когда интересующее нас свойство выполняется, но вычисленная по этому алгоритму граница оказывается недостаточно строгой, чтобы наличие этого свойства можно было формально доказать. Однако получив границу, мы получаем формальную гарантию отсутствия нарушений данного свойства. На рис. ниже этот подход проиллюстрирован графически.

Этот подход позволяет нам расширить применимость алгоритмов верификации на сети более общего назначения (активаторные функции, архитектуры), общие спецификации и более сложные модели ГО (генеративные модели, нейронные процессы, и т.п.) и спецификации, выходящие за пределы состязательной надёжности (Qin, 2018).
Перспективы
У развёртывания МО в ситуациях с высоким риском есть свои уникальные вызовы и трудности, и для этого требуется разработка технологий оценки, гарантированно обнаруживающих маловероятные ошибки. Мы считаем, что последовательное обучение по спецификациям может значительно улучшить эффективность работы по сравнению с теми случаями, когда спецификации возникают неявно из тренировочных данных. Мы с нетерпением ожидаем результатов текущих исследований состязательной оценки, надёжных моделей обучения и верификации формальных спецификаций.
Потребуется ещё много работы для того, чтобы мы смогли создавать автоматизированные инструменты, гарантирующие, что системы ИИ в реальном мире будут всё «делать правильно». В частности мы очень рады прогрессу в следующих направлениях:
- Обучение для состязательной оценки и верификации. С масштабированием и усложнением ИИ-систем становится всё сложнее проектировать алгоритмы состязательной оценки и верификации, достаточно адаптированные к модели ИИ. Если мы сможем использовать всю мощь ИИ для оценки и верификации, этот процесс можно будет масштабировать.
- Разработка публично доступных инструментов для состязательной оценки и верификации: важно обеспечить инженеров и других использующих ИИ людей простыми в использовании инструментами, проливающими свет на возможные режимы отказа системы ИИ до того, как этот отказ приведёт к обширным отрицательным последствиям. Это потребует определённой стандартизации состязательных оценок и алгоритмов верификации.
- Расширение спектра состязательных примеров. Пока что большая часть работы по состязательным примерам концентрируется на устойчивости моделей к малым изменениям, обычно в области картинок. Это стало отличным испытательным полигоном для разработки подходов к состязательным оценкам, надёжному обучению и верификации. Мы начали изучать различные спецификации для свойств, имеющих непосредственное отношение к реальному миру, и с интересом ждём результатов будущих исследований в этом направлении.
- Спецификации обучения. Спецификации, описывающие «правильное» поведение ИИ-систем часто трудно сформулировать точно. Поскольку мы создаём всё более интеллектуальные системы, способные на сложное поведение и работу в неструктурированном окружении, нам нужно будет научиться создавать системы, способные использовать частично сформулированные спецификации, а дальнейшие спецификации получать из обратной связи.
DeepMind настроена на положительное влияние на социум путём ответственной разработки и развёртывания МО-систем. Чтобы убедиться, что вклад разработчиков будет гарантированно положительным, нам нужно справиться со множеством технических препятствий. Мы намерены сделать свой вклад в эту область и с удовольствием работаем с сообществом над решением этих проблем.


scp1001
Нейросети, хоть и выдают отличные и превосходящие другие экспертные системы ответы, как правило не предоставляют информацию или алгоритм того, каким образом они этот ответ получили, и являются неким подобием чёрного ящика.
Поэтому важным направлением работы современных исследователей является внесение ясности в работу нейросетей, и визуализация того как они находят решение: habr.com/ru/post/401687
Очень интересно, что здесь нашли применение и формальные методы.
Формальная верификация является отличной альтернативой полному перебору:
она хорошо справляется с астрономическим числом комбинаций входных и выходных данных, при этом ничего не упуская и предоставляя всё то же 100% покрытие всех вариантов.
Хоть формальная верификация и используется уже несколько десятков лет, но её применение в областях, связанных с синтезом алгоритмов и машинным обучением, является ещё очень новым и свежим направлением.