«Сапёр» (Minesweeper) — это простая игра с простыми правилами, однако некоторые её конфигурации создают любопытные трудности. В этой статье мы создадим солвер «Сапёра» с увеличивающейся сложностью, и поразмышляем над тем, как меняется динамика игры при постепенном повышении уровня помощи. В конце мы разработаем новый вариант игры с гораздо более интересным геймплеем.

Локальные рассуждения: ноль соседних мин

В оригинальной игре используется один автоматический механизм: когда игрок открывает клетку, рядом с которой нет мин, движок игры открывает все соседние клетки. Это ничем не угрожает игре, поэтому можно спокойно позволить компьютеру это сделать, а сама ситуация сразу же понятна игроку и никак не мешает геймплею.

Такое рассуждение совершенно локально: для принятия решения о следующем действии учитывается информация только одной клетки.

Сложно придумать ситуацию, в которой игра стала бы хуже без этой автоматической помощи. Попробуйте сыграть в такую игру, чтобы получить представление о том, как она проходит без автоматического открытия клеток [в оригинале статьи все примеры интерактивны]:

Локальные рассуждения с учётом окружения

Новому игроку несложно будет понять, что если количество соседних мин, то есть число, показанное в клетке, равно количеству неоткрытых соседних клеток, то все эти клетки должны быть минами, поэтому на них надо поставить флажки. Аналогично, когда количество соседних мин равно количеству соседних флагов, то оставшиеся неоткрытыми соседние клетки должны быть пусты.

В этих правилах учитывается одна клетка, а также состояние соседних (открыты/поставлен флажок).

Реализация этих правил вручную может быть увлекательной. Если добавить таймер, то игрок начинает учиться применять их быстро и точно. Это превращает «Сапёра» в игру на реакцию. Что произойдёт, если мы автоматизируем эти правила?


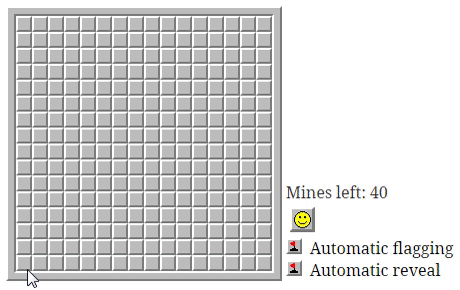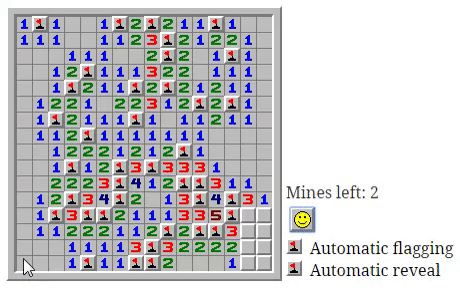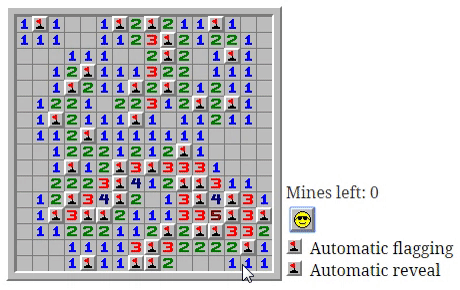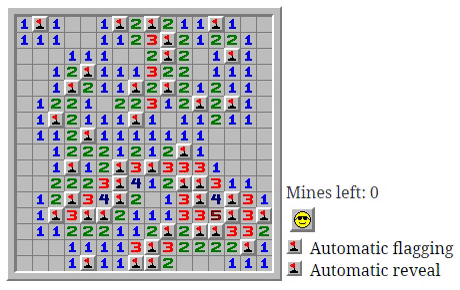
У подобной автоматизации есть интересный побочный эффект — установка флажка может мгновенно иметь фатальные последствия.

В остальном у нас могут возникнуть ситуации, которые можно разбить на три категории:

1. Игры, полностью разрешаемые применением автоматических правил
2. Сложные ситуации, требующие для рассуждений большего количества клеток
3. Состояния игры, в которых нет логического пути вперёд — игроку остаётся только выбирать случайно, возможно с учётом вероятностей.

Ситуация 1 кажется красивой, но не особо интересной, если будет возникать слишком часто. Будут ли такие игры лучше без автоматического решения? Может быть и нет; такие игры очень просты даже при решении вручную, и игроку не особо интересно играть в игры, в которых нет трудностей. Хотя, разумеется, в игре на реакцию сложность есть всегда: нужно действовать как можно быстрее.

Очень привлекательной мне кажется ситуация 2. Мы больше сосредотачиваемся на решении логических условий, меньше тратя время на точное прицеливание и нажимание правильных кнопок. Это делает «Сапёра» больше похожим на активную головоломку.

Ситуация 3 полностью разрушает всю увлекательность. Впрочем, я слышал, что некоторым людям нравится играть в игры со случайностью.

Можно ли избавиться от ситуации 3?

Полное решение: глобальные рассуждения

Для алгоритмического обнаружения всех необходимых для состояния игры логических условий нам нужно выполнить исчерпывающий поиск всех состояний игры. Доказано, что Minesweeper — это NP-полная задача. Ниже показан небольшой, но интересный и наглядный пример состояния игры, имеющий всего одно логическое решение, но для его нахождения необходимо учитывать состояние игры целиком:


Возможно ли выполнить поиск по всему пространству состояний игры? Сколько всего существует вариантов состояний s?

Дано:

w = ширина поля

h = высота поля

k = количество мин

n = w · h

Тогда количество возможных состояний s равно

$$

Для стандартных уровней «Новичок», «Любитель» и «Профессионал» это даёт нам:

$$

$$

$$

Мы понимаем, что наивный подход здесь совершенно не подходит. Давайте посмотрим, как бы мог выглядеть наивный алгоритм, и узнаем, можно ли его оптимизировать в нечто работающее.

Наивный алгоритм

Задача алгоритма — найти все необходимые для заданного состояния поля логические условия. Было бы сложно реализовать это тщательным продумыванием решений; компьютер гораздо лучше справляется с быстрым выполнением кучи глупых действий.

Что мы можем сделать «глупого»: сгенерировать все возможные перестановки позиций мин для всех оставшихся мин. Если такая перестановка соответствует всем открытым числам, то она будет правильным решением игры. Затем мы изучаем все возможные перестановки, находим все возможные решения, но по-прежнему не знаем, какое из них является верным.

Если во всех возможных решениях есть что-то общее, или среди открытых клеток, или среди клеток, помеченных как мины, то мы понимаем, что это общее должно быть частью верного решения для текущего поля. И в самом деле: невозможно создать верного решения, не имеющего таких совпадающих элементов, иначе бы мы их обнаружили.

Таким образом мы можем найти все необходимые для текущего состояния поля логические условия.

Клетки с ограничениями и без ограничений

У приведённого выше алгоритма есть очевидная проблема: количество состояний, которое ему нужно исследовать. Но не все клетки одинаковы. Неоткрытые клетки, находящиеся рядом с числом, очевидно ограничены этим числом. Мы назовём эти клетки ограниченными. Оставшиеся клетки мы назовём неограниченными.

Если мы реализуем приведённый выше алгоритм, но будем выполнять поиск только в пространстве состояний ограниченных клеток, и будем возвращаться назад, как только нарушим ограничение, то во многих играх сможем решить все логические условия за разумный промежуток времени:


В случае неограниченных клеток мы никак не можем узнать, где расположены мины, и логически сразу знаем об этом. Это означает, что можно исключить их из вычисления и рассматривать только расположение мин рядом с открытыми числами.

Однако мы знаем, что некое количество мин может попасть во множество неограниченных клеток; если есть 6 мин и 4 ограниченных клетки, то в ограниченных клетках может быть максимум 4 мины, то есть не менее 2 мин должно находиться в неограниченных клетках. По аналогичной логике мы иногда можем определить, что все неограниченные клетки должны быть пустыми или все содержать мины.

В показанном ниже случае мы знаем позиции всех мин, поэтому ИИ должен быть способен понять, что оставшиеся ячейки не заняты:


В следующем случае мы не знаем позиций всех мин, но можем понять, что оставшуюся мину нужно поместить в одну из двух клеток слева вверху. Это значит, что оставшаяся в правом нижнем углу клетка свободна:

Версия со случайностью

Если мы автоматически будем запускать глобальный солвер, то получим оптимизированную по случайности версию «Сапёра»:


Можно разделить игры в этой версии на три категории:

1. Игры, в которых игрок делает произвольный выбор и выигрывает.
2. Игры, в которых игрок делает произвольный выбор и проигрывает.
3. Игры, в которых работа ИИ требует много времени, и игрок на самом деле может использовать рассуждения.

Очевидно, что это игра со случайностями. В чём же привлекательность таких игр? С точки зрения логики показанная выше игра схожа с такой:


Но какая из игр со случайностями лучше? Похоже, что смысл других игр со случайностями заключается в существовании сложной связи между действиями игрока и победой/проигрышем. Для вытягивания номеров лотереи используются сложные машины, которые специально не торопятся в выборе номера и делают из показа этого номера целое шоу.

Возможно, большое поле, которое решается автоматически, является довольно хорошей игрой
со случайностями, учитывая то, что игрок наблюдает за постепенным открыванием всех клеток.

Можем ли мы придумать другой тип игры?

Детерминированная версия

Теперь у нас есть ИИ, способный определять все логичные шаги из заданного состояния игры. Иногда он не сможет находит логичных шагов. В таких ситуациях игроку приходится угадывать и он может проиграть, если ему не повезёт.

Что если мы добавим ещё одно правило? Когда у игры нет логичного пути вперёд, то мы можем попросить о помощи. Если ИИ соглашается, что игрок не может ничего поделать, то приходит ему на помощь. В противном случае игрок немедленно проигрывает. Это может быть интересным. Какой может быть такая помощь? Возможно, нужно открыть одну клетку, вне зависимости от наличия в ней мины:


Таким образом, мы полностью избавились от ситуаций, в которых можно было проиграть случайно.

Однако тут есть одно исключение: по-прежнему существует вероятность вырожденных ситуаций, в которых глобальный солвер не может закончить вычисления за разумный промежуток времени. К сожалению, это неизбежный результат того, что задача «Сапёра» NP-полная.

Как кнопка «Попросить помощи» влияет на игровой процесс? Она приводит тому, что игра больше сосредотачивается на логике; это самый «головоломный» вариант «Сапёра». Кто-то может подумать, что игра станет проще, но на самом деле она усложняется. Теперь ошибкам игрока нет оправданий, и кнопка накажет его, если он что-то упустил. Без кнопки легко прийти к выводу, что ты исчерпал все логичные возможности и единственный вариант развития событий — попытаться угадать случайным образом. Но из-за существования кнопки игрок обязан быть прав в этой оценке.

В заключение

Реализовав полный солвер «Сапёра», мы смогли создать разновидность игры, избавленной от её проклятья: теперь невозможно проиграть из-за того, что приходится выбирать случайно, когда уже почти решил всё поле. Эта версия отличается от оригинальной игры только в те моменты, когда нужно угадывать случайным образом, поэтому могу предположить, что она намного увлекательнее, чем оригинальная игра.

Кроме того, мы разработали вариант игры, автоматически решающий простые локальные правила. Стоит ли использовать такую помощь — зависит только от вас. Она смещает фокус игры с механического щёлканья к более головоломному игровому процессу. При этом необязательно пользоваться усовершенствованием геймплея, которое обеспечивает кнопка «Попросить помощи».