У динамического программирования репутация метода, который вы изучаете в университете, а затем вспоминаете только на собеседованиях. Но на самом деле метод применим во многих ситуациях. По сути, это техника эффективного решения задач, которые можно разбить на множество сильно повторяющихся подзадач.
В статье я покажу интересное реальное применение динамического программирования — задача вырезания швов (seam carving). Задача и методика подробно описаны в работе Авидана и Шамира «Вырезание швов для изменения размеров изображения с учётом контента» (статья в свободном доступе).
Эта одна из серии статей по динамическому программированию. Если хотите освежить в памяти методы, см. иллюстрированное введение в динамическое программирование.
Чтобы решить с помощью динамического программирования реальную проблему, нужно правильно её сформулировать. В этом разделе описываются необходимые преднастройки для выбранной задачи.
Авторы оригинальной статьи описывают контентно-ориентированное изменение размера изображения, то есть изменение ширины или высоты изображения с учётом содержимого. Подробности смотрите в оригинальной работе, а я предлагаю краткий обзор. Предположим, вы хотите изменить размер фотографии сёрфера:

Вид сверху сёрфера посреди спокойного океана, с турбулентными волнами справа. Фото: Кирил Добрев на Pixabay
Как подробно описано в статье, есть несколько способов уменьшения ширины изображения: это стандартные обрезка и масштабирование, с их присущими недостатками, а также удаление столбцов пикселей из середины. Как вы можете представить, это оставляет на фотографии видимый шов, где изображение слева и справа не совпадают. И таким способом можно удалить только ограниченный объём изображения.

Попытка уменьшить ширину путём обрезки левой части и вырезания блока из середины. Последнее оставляет видимый шов
Авидан и Шамир в статье описывают новую технику «вырезания швов» (seam carving). Она сначала определяет менее важные «низкоэнергетические» области, а затем вычисляет низкоэнергетические «швы», которые проходят по картинке. В случае уменьшения ширины изображения определяется вертикальный шов от верхней части изображения к нижней, который на каждой строке смещается влево или вправо не более чем на один пиксель.
На фотографии сёрфера самый низкоэнергетический шов проходит через середину изображения, где вода самая спокойная. Это соответствует нашей интуиции.

Самый низкоэнергетический шов, найденный на изображении сёрфера, показан красной линией шириной пять пикселей для видимости, хотя на самом деле шов его ширина всего один пиксель
Определив шов с наименьшей энергией, а затем удалив его, мы уменьшаем ширину изображения на один пиксель. Повторение этого процесса снова и снова позволяет существенно уменьшить ширину всей фотографии.

Изображение серфера после уменьшение ширины на 1024 пикселя
Опять же, алгоритм вполне логично удалил неподвижную воду посередине, а также в левой части фотографии. Но в отличие от кадрирования, сохраняется текстура воды слева и нет резких переходов. Правда, можно найти некоторые неидеальные переходы в центре, но в основном результат выглядит естественно.
Магия в том, чтобы найти самый низкоэнергетический шов. Для этого мы сначала назначаем каждому пикселю изображения энергию. Затем применяем динамическое программирование, чтобы найти путь через изображениес наименьшей энергией — этот алгоритм подробно обсудим в следующем разделе. Сначала рассмотрим, как присвоить пикселям значения энергии.
В научной статье рассматриваются несколько энергетических функций и их различия. Не будем усложнять и возьмём функцию, которая просто фиксирует величину изменения цвета вокруг каждого пикселя. Для полноты картины я немного подробнее опишу энергетическую функцию на случай, если вы захотите реализовать её самостоятельно, но это просто предварительная установка для последующих вычислений динамического программирования.

Слева три пикселя от тёмного до светлого. Разница между первым и последним велика. Справа три тёмных пикселя с небольшой разностью в интенсивности цвета
Для вычисления энергии конкретного пикселя смотрим на пиксели слева и справа от него. Покомпонентно вычисляем квадрат расстояния между ними, то есть квадрат разницы между красными, зелёными и синими компонентами, а затем складываем их. То же самое делаем для пикселей выше и ниже центрального. Наконец, складываем горизонтальные и вертикальные расстояния.
Единственное предостережение — скажем, если пиксель на левом краю, то слева нет соседа. В этом случае производим сравнение только с правым пикселем. Аналогичные проверки производим для пикселей на верхнем, правом и нижнем краях.
Функция энергии велика, если соседние пиксели сильно отличаются по цвету, и мала, если они похожи.
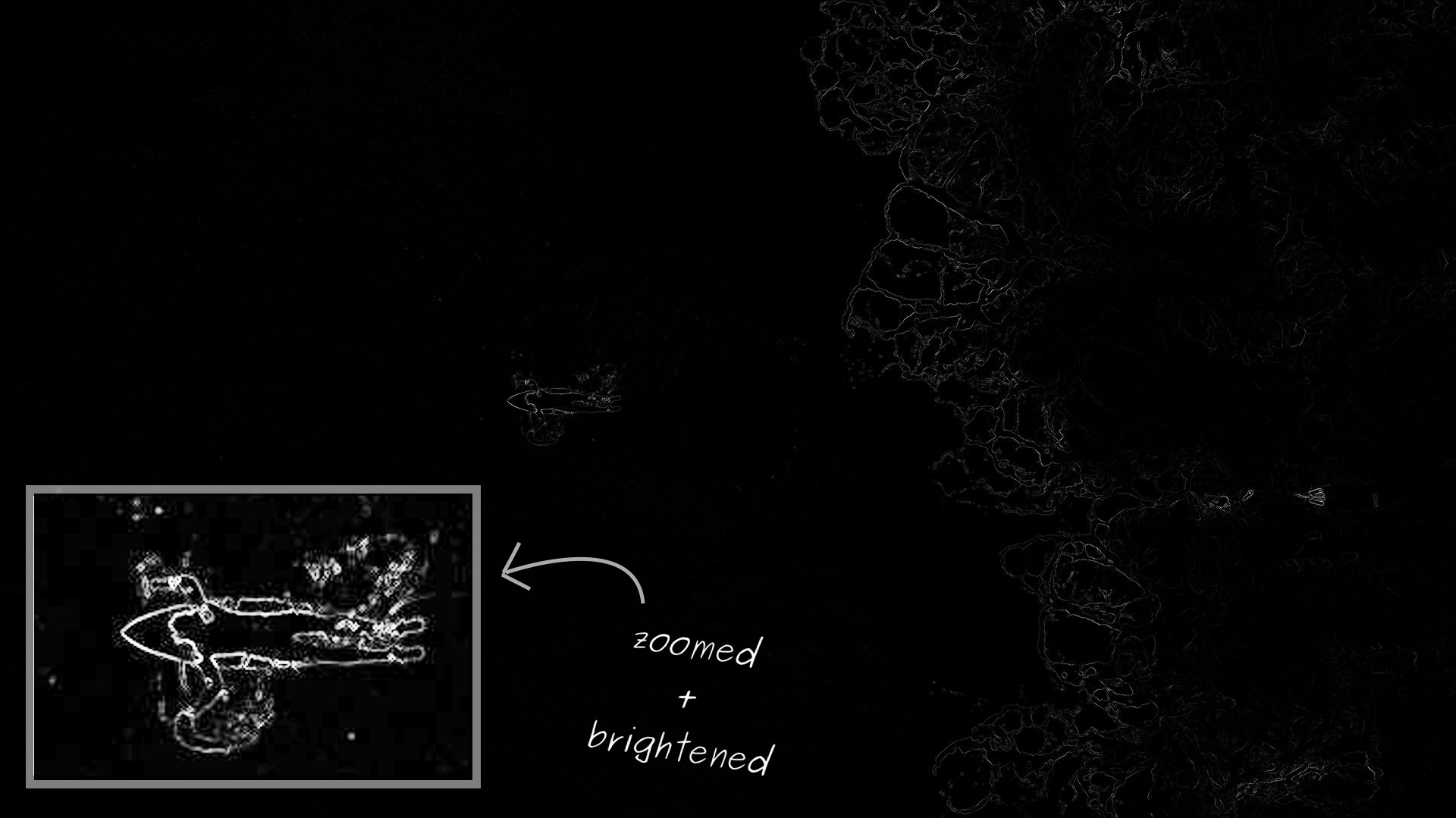
Энергия каждого пикселя на фотографии сёрфера: чем светлее — тем она выше. Как и ожидалось, самая высокая энергия у сёрфингиста в середине и турбулентных волн справа
Функция энергии хорошо работает на фотографии сёрфера. Однако она принимает очень большой диапазон значений. Поэтому при визуализации кажется, что на большей части фотографии у пикселей нулевая энергия. На самом деле там просто очень низкие значения по сравнению с регионами с самой высокой энергией. Чтобы упростить визуализацию, я зуммировал сёрфера и осветил эту область.
Вычислив энергию каждого пикселя, мы можем найти шов с наименьшей энергией от верхней части изображения к нижней. Такой же анализ применим и для горизонтальных швов для уменьшения высоты исходного изображения. Однако мы сосредоточимся на вертикальных.
Начнём с определения:
Важно заметить, что шов с наименьшей энергией не обязательно проходит через все пиксели с наименьшей энергией. Учитывается общая энергия всех, а не отдельных пикселей.

Жадный подход не работает. Выбирая низкоэнергетический пиксель на ранней стадии, мы застреваем в высокоэнергетической области изображения (красный путь справа)
Как видим, нельзя просто выбирать пиксель с наименьшей энергией в следующей строке.
Проблема с жадным подходом в том, что при принятии решения о следующем шаге мы не учитываем остальную часть шва впереди. Мы не можем заглянуть в будущее, однако способны учесть всё, что нам уже известно к настоящему моменту.
Давайте перевернём задачу с ног на голову. Вместо выбора между несколькими пикселями для продолжения одного шва, будем выбирать между несколькими швами для перехода к одному пикселю. Что нам нужно сделать, так это взять каждый пиксель и выбрать между пикселями в строке выше, от которых может исходить шов. Если каждый из пикселей в строке выше кодирует путь, пройденный до этой точки, то мы по сути смотрим на полную историю до этой точки.

Для каждого пикселя изучаем по три пикселя в строке выше. Фундаментальный выбор — какой из швов продолжать?
Это предполагает наличие подзадачи для каждого пикселя на изображении. Подзадача должна найти лучший путь до конкретного пикселя, поэтому хорошей идеей будет ассоциировать с каждым пикселем энергию самого низкоэнергетического шва, который заканчивается в этом пикселе.
В отличие от жадного подхода, вышеуказанный подход по существу пробует все возможные пути через изображение. Просто при проверке всех возможных путей одни и те же подзадачи решаются снова и снова, что делает этот подход идеальным вариантом для динамического программирования.
Как обычно, теперь нужно формализовать идею в рекуррентное соотношение. Существует подзадача, соответствующая каждому пикселю в исходном изображении, поэтому входы в наше рекуррентное соотношение могут быть просто координатами и этого пикселя. Это даёт целочисленные входы, позволяя легко упорядочивать подзадачи, а также возможность хранить ранее вычисленные значения в двумерном массиве.
Определим функцию , которая представляет энергию вертикального шва с наименьшей энергией. Он начинается в верхней части изображения и заканчивается в пикселе . Название выбрано как в оригинальной научной статье.
Во-первых, нужен базовый вариант. У всех швов, которые завершаются в верхней строке, длина всего один пиксель. Таким образом, шов с минимальной энергией — это просто пиксель с минимальной энергией:
Для пикселей в остальных строках смотрим на пиксели сверху. Поскольку шов должен быть непрерывным, то учитываем только три пикселя, расположенные слева вверху, сверху и справа вверху. Из них выбираем шов с наименьшей энергией, который завершается в одном из этих пикселей, и добавляем энергию текущего пикселя:
В качестве пограничной ситуации следует рассмотреть случай, когда текущий пиксель находится у левого или правого края изображения. В этих случаях мы опускаем для пикселей на левом краю или на правом краю.
Наконец, нужно извлечь энергию самого низкоэнергетического шва, который охватывает всю высоту изображения. Это означает, что мы смотрим на нижнюю строку изображения и выбираем самый низкоэнергетический шов, который заканчивается на одном из этих пикселей. Для фотографии шириной и высотой пикселей:
Итак, мы получили рекуррентное соотношение со всеми нужными свойствами:
Поскольку каждая подзадача соответствует одному пикселю исходного изображения, график зависимостей очень легко визуализировать. Просто разместим их на двумерной сетке, как на исходном изображении!
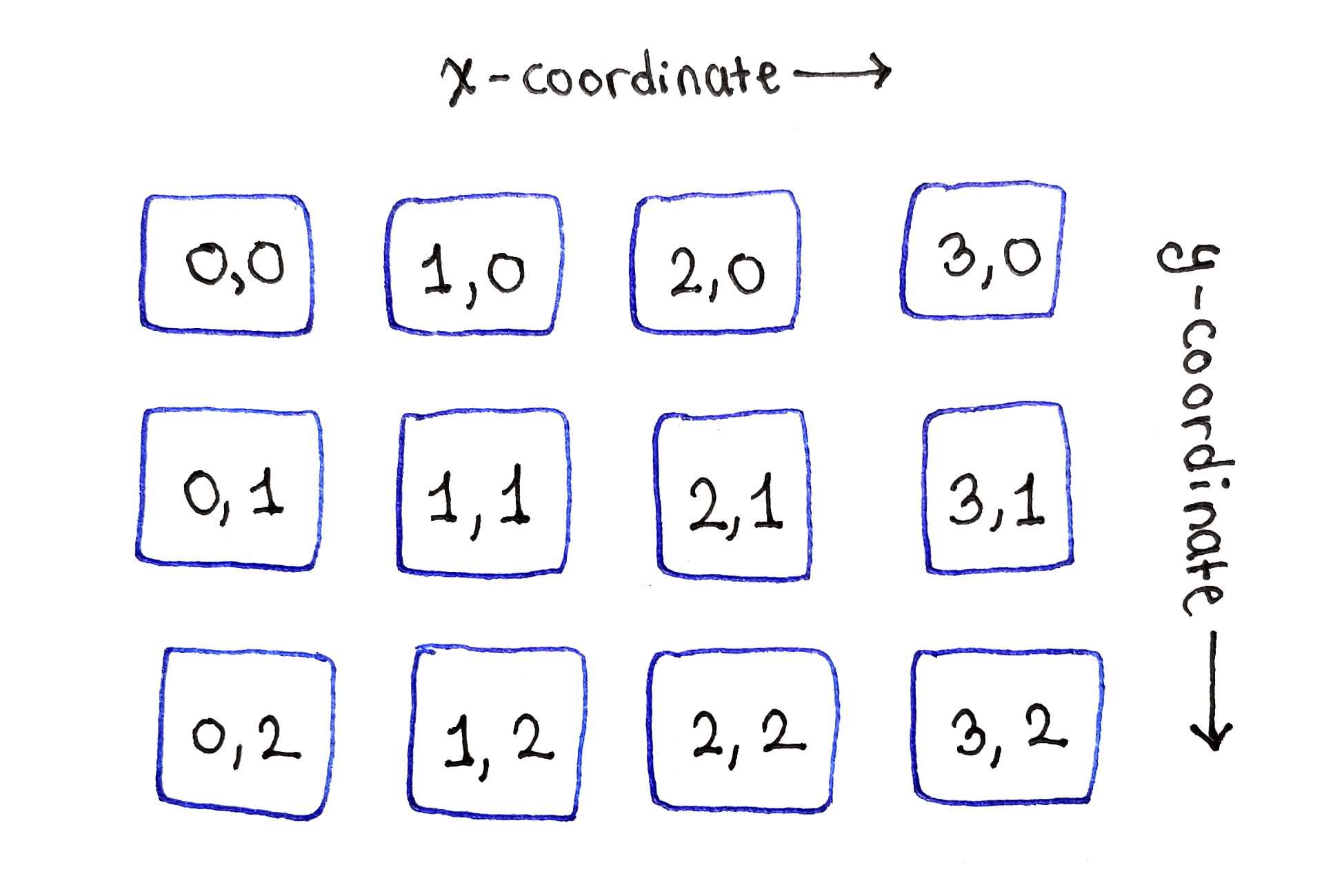
Подзадачи расположены в двумерной сетке, как и пиксели в исходном изображении
Как следует из базового сценария рекуррентного соотношения, верхнюю строку подзадач можно инициализировать значениями энергии отдельных пикселей.

Верхний ряд не зависит от других подзадач. Обратите внимание на отсутствие стрелок из верхнего ряда ячеек
Во второй строке начинают появляться зависимости. Во-первых, в самой левой ячейке во второй строке мы сталкиваемся с пограничной ситуацией. Поскольку слева ячеек нет, то ячейка зависит только от ячеек, расположенных непосредственно над ней и справа вверху. То же самое произойдёт позже с самой левой ячейкой в третьем ряду.

Подзадачи на левом краю зависят только от двух подзадач над ними
Во второй ячейке второго ряда (1,1), мы видим наиболее типичное проявление рекуррентного соотношения. Эта ячейка зависит от трёх ячеек: слева вверху, прямо над ней и справа вверху. Такая структура зависимостей применяется ко всем «средним» ячейкам во второй и последующих строках.

Подзадачи между левым и правым краями зависят от трёх подзадач сверху
Наконец, ячейка с правого края представляет вторую пограничную ситуацию. Поскольку справа больше нет ячеек, она зависит только от ячеек непосредственно вверху и вверху слева.
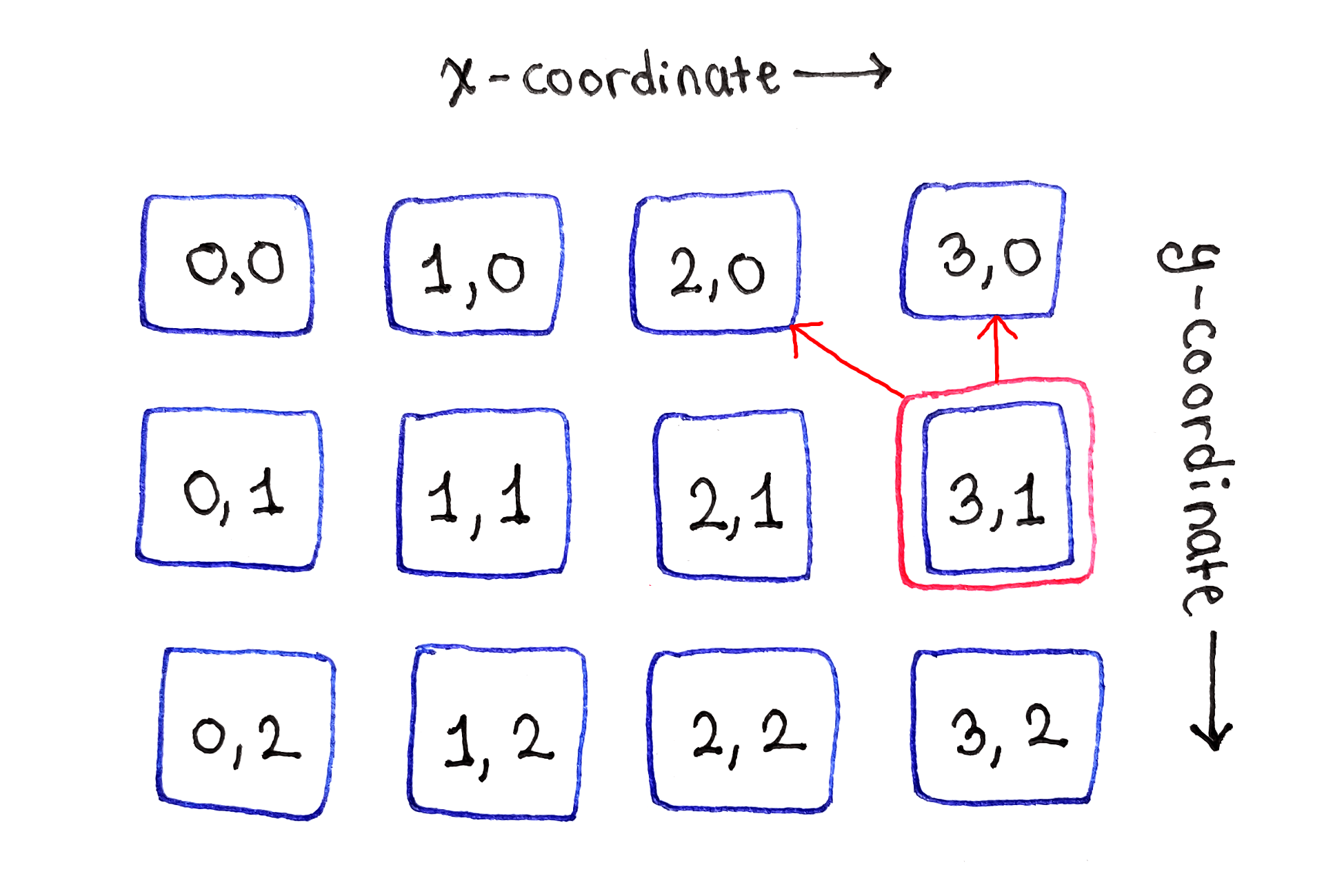
Подзадачи на правом краю зависят только от двух ячеек сверху
Процесс повторяется для всех последующих строк.

Поскольку в графе зависимостей много стрелок, эта анимация показывает зависимости для каждой подзадачи по очереди
Полный граф зависимостей пугает большим количеством стрелок, но просмотр их по одной помогает установить явные шаблоны.
Проведя этот анализ, мы получили порядок обработки:
Поскольку каждая строка зависит только от предыдущей, то нужно сохранять только две строки данных: одну для предыдущей строки и одну для текущей строки. Двигаясь слева направо, мы даже можем выбросить отдельные элементы из предыдущей строки по мере их использования. Однако это усложняет алгоритм, так как придётся выяснять, какие части предыдущей строки можно отбросить.
В следующем коде Python на входе список строк, где каждая строка содержит список чисел, представляющих отдельные энергии пикселей в этой строке. Входные данные называются
Начнём с вычисления энергии швов верхнего ряда, просто скопировав отдельные энергии пикселей в верхнем ряду:
Затем выполняем цикл по оставшимся строкам входа, вычисляя энергии шва для каждой строки. Самая «сложная» часть — определить, на какие элементы предыдущей строки ссылаться, поскольку слева от левого края или справа от правого края нет пикселей.
На каждой итерации создаётся новый список энергий шва для текущей строки. В конце итерации заменяем данные предыдущей строки данными текущей строки для следующей итерации. Вот как мы отбрасываем предыдущую строку:
В итоге
Можете проверить эту реализацию, обернув приведённый код в функцию, а потом вызвав её с двумерным массивом, который вы построили. Следующие входные данные подобраны так, чтобы жадный подход потерпел неудачу, при этом был очевидный шов с самой низкой энергией:
Каждому пикселю в исходном изображении соответствует одна подзадача. Для каждой из подзадач есть не более трёх зависимостей, поэтому решение каждой из них предполагает постоянный объём работы. Последний ряд проходится дважды. Таким образом, для изображения шириной и высотой пикселей временнaя сложность равна .
В каждый момент времени у нас хранятся два списка: один для предыдущей строки и один для текущей. В первом элементов, а второй постепенно увеличивается до . Таким образом, пространственная сложность равна , то есть просто .
Обратите внимание, что если бы мы фактически отбрасывали элементы данных предыдущей строки, то сокращали бы список элементов предыдущей строки примерно с той же скоростью, с какой нарастает список текущей строки. Таким образом, пространственная сложность останется . Хотя ширина может варьироваться, обычно это не так важно.
Итак, мы нашли значение самого низкоэнергетического шва, но что делать с этой информацией? Ведь на самом деле нас волнует не значение энергии, а сам шов! Проблема в том, что от конечного пикселя нет способа вернуться к остальной части шва.
Это то, что я пропустил в предыдущих статьях, но то же самое относится ко многим проблемам динамического программирования. Например, если вы помните задачу о грабителе домов, мы нашли максимальное значение для суммы грабежа, но не какие конкретно дома нужно ограбить для получения этой суммы.
Общий ответ: хранить обратные указатели. В задаче вырезания швов нам нужно не только значение энергии шва на каждом пикселе. Нужно ещё знать, какой из пикселей в предыдущей строке привёл к этой энергии. Сохраняя эту информацию, мы можем следовать обратным указателям вплоть до верхней строчки, получив координаты всех пикселей, которые составляют шов с наименьшей энергией.
Во-первых, создадим класс для хранения энергии и обратных указателей. Энергия будет использоваться для расчёта подзадач. Поскольку обратный указатель определяет, какой пиксель в предыдущей строке дал текущую энергию, можем представить его просто как координату x.
Результатом расчёта каждой подзадачи будет не просто число, а экземпляр этого класса.
В конце нужно пройти назад по всей высоте изображения, следуя обратным указателям, чтобы восстановить шов с наименьшей энергией. К сожалению, это означает, что нужно хранить указатели для всех пикселей изображения, а не только для предыдущей строки.
Для этого просто сохраним полный результат всех подзадач, хотя технически можно отказаться от числовых энергий шва предыдущих строк. Результаты сохраняем в двумерном массиве, который выглядит так же, как входной массив.
Начнём с первой строки, которая содержит только отдельные энергии пикселей. Поскольку предыдущей строки нет, все обратные указатели отсутствуют, но для согласованности всё равно будем хранить экземпляры
Основной цикл работает в основном так же, как и предыдущая реализация, со следующими отличиями:
Теперь вся таблица подзадач заполнена и мы можем восстановить шов с наименьшей энергией. Начнём с поиска координаты x в нижней строке, которая соответствует шву с наименьшей энергией:
Теперь переходим от нижней части изображения к верхней, изменяя из
Так шов выстраивается снизу вверх, список потом можно прочитать в обратном порядке, если нужны координаты сверху вниз.
Временнaя сложность аналогична предыдущей, потому что нам всё равно нужно один раз обработать каждый пиксель. После просмотра последней строки и поиска шва с наименьшей энергией мы затем поднимаемся на всю высоту изображения, чтобы восстановить шов. Таким образом, для изображения временнaя сложность равна .
Что касается объёма, мы по-прежнему храним постоянный объем данных для каждой подзадачи, но теперь не отбрасываем никаких данных. Таким образом, мы используем объём .
Как только будет найден вертикальный шов с наименьшей энергией, мы можем просто скопировать пиксели из исходного изображения в новое. Каждая строка нового изображения содержит все пиксели из соответствующей строки исходного изображения, за исключением пикселя из шва с наименьшей энергией. Поскольку мы удаляем один пиксель в каждой строке, начиная с изображения , то получаем изображение .
Можем повторить этот процесс, пересчитав энергетическую функцию на новом изображении и найдя на нём самый низкоэнергетический шов. Кажется заманчивым найти более одного низкоэнергетического шва в исходном изображении, а затем удалить их все сразу. Проблема в том, что два шва могут пересечься. Когда первый удалён, второй станет недействителен, потому что в нём отсутствует один или несколько пикселей.
Анимация процесса удаления шва. Лучше смотреть в полноэкранном режиме для более чёткого просмотра швов
Каждый кадр видео представляет собой изображения на каждой итерации с наложением визуализации шва с наименьшей энергией.
В статье было много подробных объяснений, так что давайте закончим серией красивых фотографий! На следующем фото — скальное образование в Национальном парке Арчес:

Скальное образование с отверстием в Национальном парке Арчес. Фото: Майк Гоад на Flickr
Энергетическая функция для этого изображения:

Энергия каждого пикселя на фотографии: чем светлее — тем она выше. Обратите внимание на высокую энергию вокруг края отверстия
В результате вычисления получается такой шов с наименьшей энергией. Обратите внимание, что он проходит через скалу справа, входя прямо в скальное образование там, где освещённая часть на вершине скалы совпадает с цветом неба. Возможно, следует подобрать энергетическую функцию получше!

Самый низкоэнергетический шов, найденный на изображении, показан красной линией шириной пять пикселей для видимости, хотя на самом деле шов его ширина всего один пиксель
Наконец, изображение арки после изменения размера:

Арка после сжатия на 1024 пикселя
Результат определённо не идеален: многие края горы из исходного изображения искажены. Одним из улучшений может быть реализация одной из других энергетических функций, перечисленных в научной статье.
Хотя динамическое программирование обычно обсуждается в теории, но является полезным практическим методом для решения сложных проблем. В этой статье мы рассмотрели одно из приложений динамического программирования: изменение размера изображения с учётом контента путём вырезания швов.
Мы применили те же принципы разбиения задачи на более мелкие подзадачи, анализируя зависимости между этими подзадачами, а затем решая подзадачи в порядке, минимизирующем пространственные и временные сложности алгоритма. Кроме того, мы изучили использование обратных указателей, чтобы не только найти значение энергии для оптимального шва, но и определить координаты каждого пикселя, которые составили это значение. Затем применили эти части к реальной проблеме, которая требует некоторой пред- и постобработки для действительно эффективного использования алгоритма динамического программирования.
В статье я покажу интересное реальное применение динамического программирования — задача вырезания швов (seam carving). Задача и методика подробно описаны в работе Авидана и Шамира «Вырезание швов для изменения размеров изображения с учётом контента» (статья в свободном доступе).
Эта одна из серии статей по динамическому программированию. Если хотите освежить в памяти методы, см. иллюстрированное введение в динамическое программирование.
Изменение размеров изображения с учётом контента
Чтобы решить с помощью динамического программирования реальную проблему, нужно правильно её сформулировать. В этом разделе описываются необходимые преднастройки для выбранной задачи.
Авторы оригинальной статьи описывают контентно-ориентированное изменение размера изображения, то есть изменение ширины или высоты изображения с учётом содержимого. Подробности смотрите в оригинальной работе, а я предлагаю краткий обзор. Предположим, вы хотите изменить размер фотографии сёрфера:

Вид сверху сёрфера посреди спокойного океана, с турбулентными волнами справа. Фото: Кирил Добрев на Pixabay
Как подробно описано в статье, есть несколько способов уменьшения ширины изображения: это стандартные обрезка и масштабирование, с их присущими недостатками, а также удаление столбцов пикселей из середины. Как вы можете представить, это оставляет на фотографии видимый шов, где изображение слева и справа не совпадают. И таким способом можно удалить только ограниченный объём изображения.

Попытка уменьшить ширину путём обрезки левой части и вырезания блока из середины. Последнее оставляет видимый шов
Авидан и Шамир в статье описывают новую технику «вырезания швов» (seam carving). Она сначала определяет менее важные «низкоэнергетические» области, а затем вычисляет низкоэнергетические «швы», которые проходят по картинке. В случае уменьшения ширины изображения определяется вертикальный шов от верхней части изображения к нижней, который на каждой строке смещается влево или вправо не более чем на один пиксель.
На фотографии сёрфера самый низкоэнергетический шов проходит через середину изображения, где вода самая спокойная. Это соответствует нашей интуиции.

Самый низкоэнергетический шов, найденный на изображении сёрфера, показан красной линией шириной пять пикселей для видимости, хотя на самом деле шов его ширина всего один пиксель
Определив шов с наименьшей энергией, а затем удалив его, мы уменьшаем ширину изображения на один пиксель. Повторение этого процесса снова и снова позволяет существенно уменьшить ширину всей фотографии.

Изображение серфера после уменьшение ширины на 1024 пикселя
Опять же, алгоритм вполне логично удалил неподвижную воду посередине, а также в левой части фотографии. Но в отличие от кадрирования, сохраняется текстура воды слева и нет резких переходов. Правда, можно найти некоторые неидеальные переходы в центре, но в основном результат выглядит естественно.
Определение энергии изображения
Магия в том, чтобы найти самый низкоэнергетический шов. Для этого мы сначала назначаем каждому пикселю изображения энергию. Затем применяем динамическое программирование, чтобы найти путь через изображениес наименьшей энергией — этот алгоритм подробно обсудим в следующем разделе. Сначала рассмотрим, как присвоить пикселям значения энергии.
В научной статье рассматриваются несколько энергетических функций и их различия. Не будем усложнять и возьмём функцию, которая просто фиксирует величину изменения цвета вокруг каждого пикселя. Для полноты картины я немного подробнее опишу энергетическую функцию на случай, если вы захотите реализовать её самостоятельно, но это просто предварительная установка для последующих вычислений динамического программирования.

Слева три пикселя от тёмного до светлого. Разница между первым и последним велика. Справа три тёмных пикселя с небольшой разностью в интенсивности цвета
Для вычисления энергии конкретного пикселя смотрим на пиксели слева и справа от него. Покомпонентно вычисляем квадрат расстояния между ними, то есть квадрат разницы между красными, зелёными и синими компонентами, а затем складываем их. То же самое делаем для пикселей выше и ниже центрального. Наконец, складываем горизонтальные и вертикальные расстояния.
Единственное предостережение — скажем, если пиксель на левом краю, то слева нет соседа. В этом случае производим сравнение только с правым пикселем. Аналогичные проверки производим для пикселей на верхнем, правом и нижнем краях.
Функция энергии велика, если соседние пиксели сильно отличаются по цвету, и мала, если они похожи.

Энергия каждого пикселя на фотографии сёрфера: чем светлее — тем она выше. Как и ожидалось, самая высокая энергия у сёрфингиста в середине и турбулентных волн справа
Функция энергии хорошо работает на фотографии сёрфера. Однако она принимает очень большой диапазон значений. Поэтому при визуализации кажется, что на большей части фотографии у пикселей нулевая энергия. На самом деле там просто очень низкие значения по сравнению с регионами с самой высокой энергией. Чтобы упростить визуализацию, я зуммировал сёрфера и осветил эту область.
Поиск низкоэнергетических швов с помощью динамического программирования
Вычислив энергию каждого пикселя, мы можем найти шов с наименьшей энергией от верхней части изображения к нижней. Такой же анализ применим и для горизонтальных швов для уменьшения высоты исходного изображения. Однако мы сосредоточимся на вертикальных.
Начнём с определения:
- Шов — это последовательность пикселей, по одному пикселю на строку. Требование состоит в том, что между двумя последовательными строками координата изменяется не более чем на один пиксель. Это сохраняет последовательность шва.
- Шов с наименьшей энергией — тот, чья полная энергия по всем пикселям в шве минимизирована.
Важно заметить, что шов с наименьшей энергией не обязательно проходит через все пиксели с наименьшей энергией. Учитывается общая энергия всех, а не отдельных пикселей.

Жадный подход не работает. Выбирая низкоэнергетический пиксель на ранней стадии, мы застреваем в высокоэнергетической области изображения (красный путь справа)
Как видим, нельзя просто выбирать пиксель с наименьшей энергией в следующей строке.
Разбиваем проблему на подзадачи
Проблема с жадным подходом в том, что при принятии решения о следующем шаге мы не учитываем остальную часть шва впереди. Мы не можем заглянуть в будущее, однако способны учесть всё, что нам уже известно к настоящему моменту.
Давайте перевернём задачу с ног на голову. Вместо выбора между несколькими пикселями для продолжения одного шва, будем выбирать между несколькими швами для перехода к одному пикселю. Что нам нужно сделать, так это взять каждый пиксель и выбрать между пикселями в строке выше, от которых может исходить шов. Если каждый из пикселей в строке выше кодирует путь, пройденный до этой точки, то мы по сути смотрим на полную историю до этой точки.

Для каждого пикселя изучаем по три пикселя в строке выше. Фундаментальный выбор — какой из швов продолжать?
Это предполагает наличие подзадачи для каждого пикселя на изображении. Подзадача должна найти лучший путь до конкретного пикселя, поэтому хорошей идеей будет ассоциировать с каждым пикселем энергию самого низкоэнергетического шва, который заканчивается в этом пикселе.
В отличие от жадного подхода, вышеуказанный подход по существу пробует все возможные пути через изображение. Просто при проверке всех возможных путей одни и те же подзадачи решаются снова и снова, что делает этот подход идеальным вариантом для динамического программирования.
Определение рекуррентного соотношения
Как обычно, теперь нужно формализовать идею в рекуррентное соотношение. Существует подзадача, соответствующая каждому пикселю в исходном изображении, поэтому входы в наше рекуррентное соотношение могут быть просто координатами и этого пикселя. Это даёт целочисленные входы, позволяя легко упорядочивать подзадачи, а также возможность хранить ранее вычисленные значения в двумерном массиве.
Определим функцию , которая представляет энергию вертикального шва с наименьшей энергией. Он начинается в верхней части изображения и заканчивается в пикселе . Название выбрано как в оригинальной научной статье.
Во-первых, нужен базовый вариант. У всех швов, которые завершаются в верхней строке, длина всего один пиксель. Таким образом, шов с минимальной энергией — это просто пиксель с минимальной энергией:
Для пикселей в остальных строках смотрим на пиксели сверху. Поскольку шов должен быть непрерывным, то учитываем только три пикселя, расположенные слева вверху, сверху и справа вверху. Из них выбираем шов с наименьшей энергией, который завершается в одном из этих пикселей, и добавляем энергию текущего пикселя:
В качестве пограничной ситуации следует рассмотреть случай, когда текущий пиксель находится у левого или правого края изображения. В этих случаях мы опускаем для пикселей на левом краю или на правом краю.
Наконец, нужно извлечь энергию самого низкоэнергетического шва, который охватывает всю высоту изображения. Это означает, что мы смотрим на нижнюю строку изображения и выбираем самый низкоэнергетический шов, который заканчивается на одном из этих пикселей. Для фотографии шириной и высотой пикселей:
Итак, мы получили рекуррентное соотношение со всеми нужными свойствами:
- У рекуррентного соотношения есть целочисленные входы.
- Из соотношения легко извлечь окончательный ответ.
- Соотношение зависит от самого себя.
Проверка подзадачи DAG (ориентированный ациклический граф)
Поскольку каждая подзадача соответствует одному пикселю исходного изображения, график зависимостей очень легко визуализировать. Просто разместим их на двумерной сетке, как на исходном изображении!

Подзадачи расположены в двумерной сетке, как и пиксели в исходном изображении
Как следует из базового сценария рекуррентного соотношения, верхнюю строку подзадач можно инициализировать значениями энергии отдельных пикселей.

Верхний ряд не зависит от других подзадач. Обратите внимание на отсутствие стрелок из верхнего ряда ячеек
Во второй строке начинают появляться зависимости. Во-первых, в самой левой ячейке во второй строке мы сталкиваемся с пограничной ситуацией. Поскольку слева ячеек нет, то ячейка зависит только от ячеек, расположенных непосредственно над ней и справа вверху. То же самое произойдёт позже с самой левой ячейкой в третьем ряду.

Подзадачи на левом краю зависят только от двух подзадач над ними
Во второй ячейке второго ряда (1,1), мы видим наиболее типичное проявление рекуррентного соотношения. Эта ячейка зависит от трёх ячеек: слева вверху, прямо над ней и справа вверху. Такая структура зависимостей применяется ко всем «средним» ячейкам во второй и последующих строках.

Подзадачи между левым и правым краями зависят от трёх подзадач сверху
Наконец, ячейка с правого края представляет вторую пограничную ситуацию. Поскольку справа больше нет ячеек, она зависит только от ячеек непосредственно вверху и вверху слева.

Подзадачи на правом краю зависят только от двух ячеек сверху
Процесс повторяется для всех последующих строк.

Поскольку в графе зависимостей много стрелок, эта анимация показывает зависимости для каждой подзадачи по очереди
Полный граф зависимостей пугает большим количеством стрелок, но просмотр их по одной помогает установить явные шаблоны.
Реализация снизу вверх
Проведя этот анализ, мы получили порядок обработки:
- Переходим от верхней части изображения к нижней.
- В каждой строке можно действовать в любом порядке. Естественный выбор — идти слева направо.
Поскольку каждая строка зависит только от предыдущей, то нужно сохранять только две строки данных: одну для предыдущей строки и одну для текущей строки. Двигаясь слева направо, мы даже можем выбросить отдельные элементы из предыдущей строки по мере их использования. Однако это усложняет алгоритм, так как придётся выяснять, какие части предыдущей строки можно отбросить.
В следующем коде Python на входе список строк, где каждая строка содержит список чисел, представляющих отдельные энергии пикселей в этой строке. Входные данные называются
pixel_energies, а pixel_energies[y][x] представляет энергию пикселя в координатах .Начнём с вычисления энергии швов верхнего ряда, просто скопировав отдельные энергии пикселей в верхнем ряду:
previous_seam_energies_row = list(pixel_energies[0])Затем выполняем цикл по оставшимся строкам входа, вычисляя энергии шва для каждой строки. Самая «сложная» часть — определить, на какие элементы предыдущей строки ссылаться, поскольку слева от левого края или справа от правого края нет пикселей.
На каждой итерации создаётся новый список энергий шва для текущей строки. В конце итерации заменяем данные предыдущей строки данными текущей строки для следующей итерации. Вот как мы отбрасываем предыдущую строку:
# Skip the first row in the following loop.
for y in range(1, len(pixel_energies)):
pixel_energies_row = pixel_energies[y]
seam_energies_row = []
for x, pixel_energy in enumerate(pixel_energies_row):
# Determine the range of x values to iterate over in the previous
# row. The range depends on if the current pixel is in the middle of
# the image, or on one of the edges.
x_left = max(x - 1, 0)
x_right = min(x + 1, len(pixel_energies_row) - 1)
x_range = range(x_left, x_right + 1)
min_seam_energy = pixel_energy + min(previous_seam_energies_row[x_i] for x_i in x_range)
seam_energies_row.append(min_seam_energy)
previous_seam_energies_row = seam_energies_rowВ итоге
previous_seam_energies_row содержит энергии шва для нижней строки. Находим минимальное значение в этом списке — и это ответ!min(seam_energy for seam_energy in previous_seam_energies_row)Можете проверить эту реализацию, обернув приведённый код в функцию, а потом вызвав её с двумерным массивом, который вы построили. Следующие входные данные подобраны так, чтобы жадный подход потерпел неудачу, при этом был очевидный шов с самой низкой энергией:
ENERGIES = [
[9, 9, 0, 9, 9],
[9, 1, 9, 8, 9],
[9, 9, 9, 9, 0],
[9, 9, 9, 0, 9],
]
print(min_seam_energy(ENERGIES))Пространственная и временнaя сложность
Каждому пикселю в исходном изображении соответствует одна подзадача. Для каждой из подзадач есть не более трёх зависимостей, поэтому решение каждой из них предполагает постоянный объём работы. Последний ряд проходится дважды. Таким образом, для изображения шириной и высотой пикселей временнaя сложность равна .
В каждый момент времени у нас хранятся два списка: один для предыдущей строки и один для текущей. В первом элементов, а второй постепенно увеличивается до . Таким образом, пространственная сложность равна , то есть просто .
Обратите внимание, что если бы мы фактически отбрасывали элементы данных предыдущей строки, то сокращали бы список элементов предыдущей строки примерно с той же скоростью, с какой нарастает список текущей строки. Таким образом, пространственная сложность останется . Хотя ширина может варьироваться, обычно это не так важно.
Обратные указатели для нахождения шва с наименьшей энергией
Итак, мы нашли значение самого низкоэнергетического шва, но что делать с этой информацией? Ведь на самом деле нас волнует не значение энергии, а сам шов! Проблема в том, что от конечного пикселя нет способа вернуться к остальной части шва.
Это то, что я пропустил в предыдущих статьях, но то же самое относится ко многим проблемам динамического программирования. Например, если вы помните задачу о грабителе домов, мы нашли максимальное значение для суммы грабежа, но не какие конкретно дома нужно ограбить для получения этой суммы.
Представление обратных указателей
Общий ответ: хранить обратные указатели. В задаче вырезания швов нам нужно не только значение энергии шва на каждом пикселе. Нужно ещё знать, какой из пикселей в предыдущей строке привёл к этой энергии. Сохраняя эту информацию, мы можем следовать обратным указателям вплоть до верхней строчки, получив координаты всех пикселей, которые составляют шов с наименьшей энергией.
Во-первых, создадим класс для хранения энергии и обратных указателей. Энергия будет использоваться для расчёта подзадач. Поскольку обратный указатель определяет, какой пиксель в предыдущей строке дал текущую энергию, можем представить его просто как координату x.
class SeamEnergyWithBackPointer():
def __init__(self, energy, x_coordinate_in_previous_row=None):
self.energy = energy
self.x_coordinate_in_previous_row = x_coordinate_in_previous_rowРезультатом расчёта каждой подзадачи будет не просто число, а экземпляр этого класса.
Хранение обратных указателей
В конце нужно пройти назад по всей высоте изображения, следуя обратным указателям, чтобы восстановить шов с наименьшей энергией. К сожалению, это означает, что нужно хранить указатели для всех пикселей изображения, а не только для предыдущей строки.
Для этого просто сохраним полный результат всех подзадач, хотя технически можно отказаться от числовых энергий шва предыдущих строк. Результаты сохраняем в двумерном массиве, который выглядит так же, как входной массив.
Начнём с первой строки, которая содержит только отдельные энергии пикселей. Поскольку предыдущей строки нет, все обратные указатели отсутствуют, но для согласованности всё равно будем хранить экземпляры
SeamEnergyWithBackPointers:seam_energies = []
# Initialize the top row of seam energies by copying over the top row of
# the pixel energies. There are no back pointers in the top row.
seam_energies.append([
SeamEnergyWithBackPointer(pixel_energy)
for pixel_energy in pixel_energies[0]
])Основной цикл работает в основном так же, как и предыдущая реализация, со следующими отличиями:
- Данные для предыдущей строки содержат экземпляры
SeamEnergyWithBackPointer, поэтому при вычислении значения рекуррентного соотношения следует искать энергию шва внутри этих объектов.
- Сохраняя данные для текущего пикселя, нужно построить новый экземпляр
SeamEnergyWithBackPointer. Здесь мы будем хранить энергию шва для текущего пикселя, а также координату x из предыдущей строки, используемую для расчёта текущей энергии шва.
- В конце каждой строки вместо того, чтобы отбрасывать данные предыдущей строки, мы просто добавляем данные текущей строки в
seam_energies.
# Skip the first row in the following loop.
for y in range(1, len(pixel_energies)):
pixel_energies_row = pixel_energies[y]
seam_energies_row = []
for x, pixel_energy in enumerate(pixel_energies_row):
# Determine the range of x values to iterate over in the previous
# row. The range depends on if the current pixel is in the middle of
# the image, or on one of the edges.
x_left = max(x - 1, 0)
x_right = min(x + 1, len(pixel_energies_row) - 1)
x_range = range(x_left, x_right + 1)
min_parent_x = min(
x_range,
key=lambda x_i: seam_energies[y - 1][x_i].energy
)
min_seam_energy = SeamEnergyWithBackPointer(
pixel_energy + seam_energies[y - 1][min_parent_x].energy,
min_parent_x
)
seam_energies_row.append(min_seam_energy)
seam_energies.append(seam_energies_row)Идём по обратным указателям
Теперь вся таблица подзадач заполнена и мы можем восстановить шов с наименьшей энергией. Начнём с поиска координаты x в нижней строке, которая соответствует шву с наименьшей энергией:
# Find the x coordinate with minimal seam energy in the bottom row.
min_seam_end_x = min(
range(len(seam_energies[-1])),
key=lambda x: seam_energies[-1][x].energy
)Теперь переходим от нижней части изображения к верхней, изменяя из
len(seam_energies) - 1 до нуля. На каждой итерации добавляем текущую пару в список, представляющий наш шов, а затем устанавливаем значение для объекта, на который указывает SeamEnergyWithBackPointer в текущей строке.# Follow the back pointers to form a list of coordinates that form the
# lowest-energy seam.
seam = []
seam_point_x = min_seam_end_x
for y in range(len(seam_energies) - 1, -1, -1):
seam.append((seam_point_x, y))
seam_point_x = seam_energies[y][seam_point_x].x_coordinate_in_previous_row
seam.reverse()Так шов выстраивается снизу вверх, список потом можно прочитать в обратном порядке, если нужны координаты сверху вниз.
Пространственная и временнaя сложность
Временнaя сложность аналогична предыдущей, потому что нам всё равно нужно один раз обработать каждый пиксель. После просмотра последней строки и поиска шва с наименьшей энергией мы затем поднимаемся на всю высоту изображения, чтобы восстановить шов. Таким образом, для изображения временнaя сложность равна .
Что касается объёма, мы по-прежнему храним постоянный объем данных для каждой подзадачи, но теперь не отбрасываем никаких данных. Таким образом, мы используем объём .
Удаление низкоэнергетических швов
Как только будет найден вертикальный шов с наименьшей энергией, мы можем просто скопировать пиксели из исходного изображения в новое. Каждая строка нового изображения содержит все пиксели из соответствующей строки исходного изображения, за исключением пикселя из шва с наименьшей энергией. Поскольку мы удаляем один пиксель в каждой строке, начиная с изображения , то получаем изображение .
Можем повторить этот процесс, пересчитав энергетическую функцию на новом изображении и найдя на нём самый низкоэнергетический шов. Кажется заманчивым найти более одного низкоэнергетического шва в исходном изображении, а затем удалить их все сразу. Проблема в том, что два шва могут пересечься. Когда первый удалён, второй станет недействителен, потому что в нём отсутствует один или несколько пикселей.
Анимация процесса удаления шва. Лучше смотреть в полноэкранном режиме для более чёткого просмотра швов
Каждый кадр видео представляет собой изображения на каждой итерации с наложением визуализации шва с наименьшей энергией.
Другой пример
В статье было много подробных объяснений, так что давайте закончим серией красивых фотографий! На следующем фото — скальное образование в Национальном парке Арчес:

Скальное образование с отверстием в Национальном парке Арчес. Фото: Майк Гоад на Flickr
Энергетическая функция для этого изображения:

Энергия каждого пикселя на фотографии: чем светлее — тем она выше. Обратите внимание на высокую энергию вокруг края отверстия
В результате вычисления получается такой шов с наименьшей энергией. Обратите внимание, что он проходит через скалу справа, входя прямо в скальное образование там, где освещённая часть на вершине скалы совпадает с цветом неба. Возможно, следует подобрать энергетическую функцию получше!

Самый низкоэнергетический шов, найденный на изображении, показан красной линией шириной пять пикселей для видимости, хотя на самом деле шов его ширина всего один пиксель
Наконец, изображение арки после изменения размера:

Арка после сжатия на 1024 пикселя
Результат определённо не идеален: многие края горы из исходного изображения искажены. Одним из улучшений может быть реализация одной из других энергетических функций, перечисленных в научной статье.
Хотя динамическое программирование обычно обсуждается в теории, но является полезным практическим методом для решения сложных проблем. В этой статье мы рассмотрели одно из приложений динамического программирования: изменение размера изображения с учётом контента путём вырезания швов.
Мы применили те же принципы разбиения задачи на более мелкие подзадачи, анализируя зависимости между этими подзадачами, а затем решая подзадачи в порядке, минимизирующем пространственные и временные сложности алгоритма. Кроме того, мы изучили использование обратных указателей, чтобы не только найти значение энергии для оптимального шва, но и определить координаты каждого пикселя, которые составили это значение. Затем применили эти части к реальной проблеме, которая требует некоторой пред- и постобработки для действительно эффективного использования алгоритма динамического программирования.
Комментарии (2)

Scf
01.07.2019 00:47Это, случаем, не разновидность задачи поиска кратчайшего пути во взвешенном графе?


KvanTTT
Идея не новая, тоже давно реализовывал подобный алгоритм: Seam-Carving-Advanced.
Интересней посмотреть как это работает на видео (там строятся трехмерные швы-поверхности) и с реализацией под GPU.