Перевод подготовлен для студентов курса «Прикладная аналитика на R».

Это была моя первая попытка выполнить кластеризацию клиентов на основе реальных данных, и она дала мне ценный опыт. В Интернете есть множество статей о кластеризации с использованием численных переменных, однако найти решения для категориальных данных, работа с которыми несколько сложнее, оказалось не так просто. Методы кластеризации категориальных данных еще только разрабатываются, и в другом посте я собираюсь попробовать еще один.
С другой стороны, многие считают, что кластеризация категориальных данных может не давать вразумительных результатов —?и это отчасти верно (см. великолепное обсуждение на сайте CrossValidated). В какой-то момент я подумала: «Что я делаю? Их же можно просто разбить на когорты». Однако когортный анализ также не всегда целесообразен, особенно при значительном количестве категориальных переменных с большим числом уровней:?разобраться с 5–7 когортами можно без труда, но если у вас 22 переменные и у каждой по 5 уровней (например, опрос клиентов с дискретными оценками 1, 2, 3, 4 и 5), и нужно понять, с какими характерными группами клиентов вы имеете дело, —?у вас получится 22x5 когорт. С такой задачей никто не захочет возиться. И тут могла бы помочь кластеризация. Так что в этом посте я расскажу о том, что сама хотела бы узнать сразу, как только занялась кластеризацией.
Сам процесс кластеризации состоит из трех шагов:
Этот пост будет своеобразным введением, описывающим основные принципы кластеризации и ее реализацию в среде R.
Основой для кластеризации станет матрица несходства, которая в математических терминах описывает, насколько точки в наборе данных отличны (удалены) друг от друга. Она позволяет в дальнейшем объединить в группы те точки, которые находятся ближе всего друг к другу, или разделить наиболее удаленные друг от друга —?в чем и состоит основная идея кластеризации.
На этом этапе важны различия между типами данных, так как матрица несходства строится на основе расстояний между отдельными точками данных. Нетрудно представить себе расстояния между точками численных данных (известный пример — евклидовы расстояния), однако в случае категориальных данных (факторы в R) все не так очевидно.
Чтобы построить матрицу несходства в этом случае, следует использовать так называемое расстояние Говера. Я не буду углубляться в математическую часть этого понятия, просто приведу ссылки: вот и вот. Для этого я предпочитаю использовать
Матрица несходства готова. Для 200 наблюдений она строится быстро, но может потребовать очень большого объема вычислений, если вы имеете дело с большим набором данных.
На практике весьма вероятно, что сначала вам придется почистить набор данных, выполнить необходимые трансформации из строк в факторы и проследить за недостающими значениями. В моем случае набор данных также содержал строки отсутствующих значений, которые каждый раз красиво собирались в кластеры, так что казалось уже, что вот оно, сокровище, — пока я не посмотрела на значения (увы!).
Возможно, вы уже знаете, что кластеризация бывает методом k-средних и иерархическая. В этом посте я фокусируюсь на втором методе, так как он более гибкий и допускает различные подходы: можно выбрать либо агломеративный (снизу вверх), либо дивизионный (сверху вниз) алгоритм кластеризации.
Источник: UC Business Analytics R Programming Guide
Агломеративная кластеризация начинается с
Дивизионная кластеризация выполняется противоположным образом —?исходно предполагается, что все n точек данных, которые у нас есть, представляют собой один большой кластер, а далее наименее схожие из них разделяются на отдельные группы.
Принимая решение о том, какой из этих способов выбрать, всегда имеет смысл попробовать все варианты, однако в целом агломеративная кластеризация лучше подходит для выявления небольших кластеров и используется большинством компьютерных программ, а дивизионная кластеризация целесообразнее?для выявления крупных кластеров.
Лично я перед тем как решить, какой метод использовать, предпочитаю взглянуть на дендрограммы —?графическое представление кластеризации. Как вы увидите далее, некоторые дендрограммы хорошо сбалансированы, а другие — весьма хаотичны.
# Основные входные данные для кода ниже — несходство (матрица расстояний)
На этом этапе необходимо сделать выбор между различными алгоритмами кластеризации и различным количеством кластеров. Вы можете использовать разные способы оценки, не забывая руководствоваться здравым смыслом. Я выделила эти слова жирным шрифтом и курсивом, потому что осмысленность выбора очень важна —?количество кластеров и способ разделения данных на группы должны быть целесообразными с практической точки зрения. Число комбинаций значений категориальных переменных конечно (так как они дискретны), однако не любая разбивка на их основе будет осмысленной. Возможно, вы не захотите также, чтобы кластеров было очень мало —?в этом случае они будут слишком обобщенными. В итоге все зависит от вашей цели и задач выполняемого анализа.
В целом, при создании кластеров вы заинтересованы в получении четко выраженных групп точек данных, так, чтобы расстояние между такими точками внутри кластера (или компактность) было минимальным, а расстояние между группами (отделимость) — максимально возможным. Это легко понять интуитивно: расстояние между точками — это мера их несходства, полученная на основе матрицы несходства. Таким образом, оценка качества кластеризации опирается на оценку компактности и отделимости.
Далее я продемонстрирую два подхода и покажу, что один из них может давать бессмысленные результаты.
На практике эти два метода часто дают разные результаты, что может привести к определенному замешательству — максимальная компактность и максимально четкое разделение будут достигаться при разном количестве кластеров, так что здравый смысл и понимание того, что на самом деле означают ваши данные, будут играть важную роль при принятии окончательного решения.
Есть также ряд метрик, которые вы можете проанализировать. Я добавлю их непосредственно в код.
Итак, показатель average.within, который представляет среднее расстояние между наблюдениями внутри кластеров, уменьшается, как и within.cluster.ss (сумма квадратов расстояний между наблюдениями в кластере). Средняя ширина силуэта (avg.silwidth) меняется не так однозначно, однако обратную зависимость все же можно заметить.
Обратите внимание, насколько непропорциональны размеры кластеров. Я бы не стала торопиться работать с несравнимым количеством наблюдений внутри кластеров. Одна из причин состоит в том, что набор данных может быть несбалансированным, и какая-то группа наблюдений будет перевешивать при анализе все остальные —?это нехорошо и с большой вероятностью приведет к погрешностям.
Обратите внимание, насколько лучше сбалансирована по количеству наблюдений на группу агломеративная иерархическая кластеризация на основе метода полной связи.
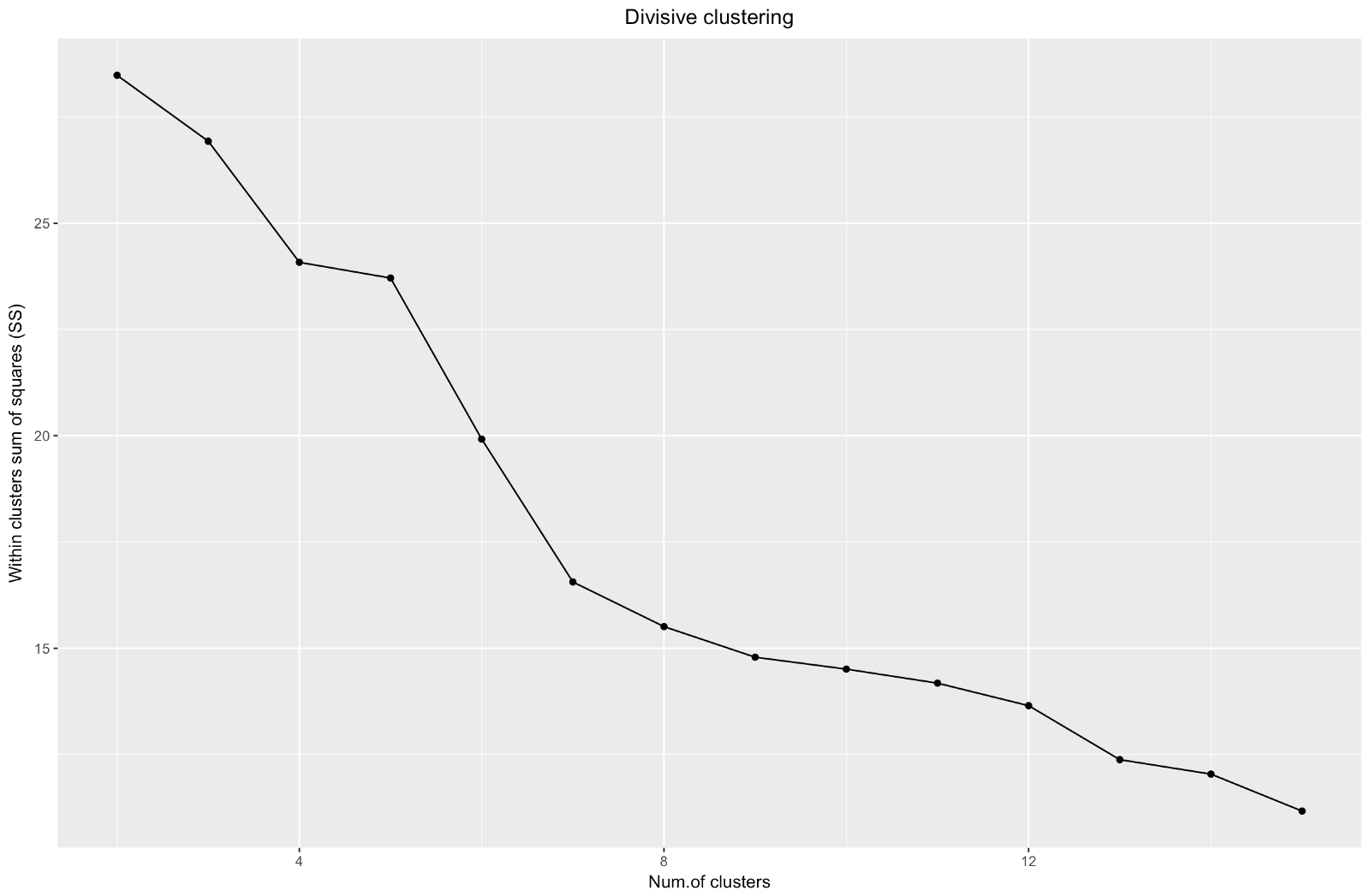
Итак, мы создали график «локтя». Он показывает, как сумма квадратов расстояний между наблюдениями (мы используем ее как меру близости наблюдений — чем она меньше, тем ближе друг к другу измерения внутри кластера)?меняется для различного количества кластеров. В идеале мы должны увидеть отчетливый «локтевой сгиб» в той точке, где дальнейшее разбиение на кластеры дает лишь незначительное уменьшение суммы квадратов (SS). Для приведенного ниже графика я бы остановилась примерно на 7. Хотя в этом случае один из кластеров будет состоять всего из двух наблюдений. Посмотрим, что произойдет при агломеративной кластеризации.
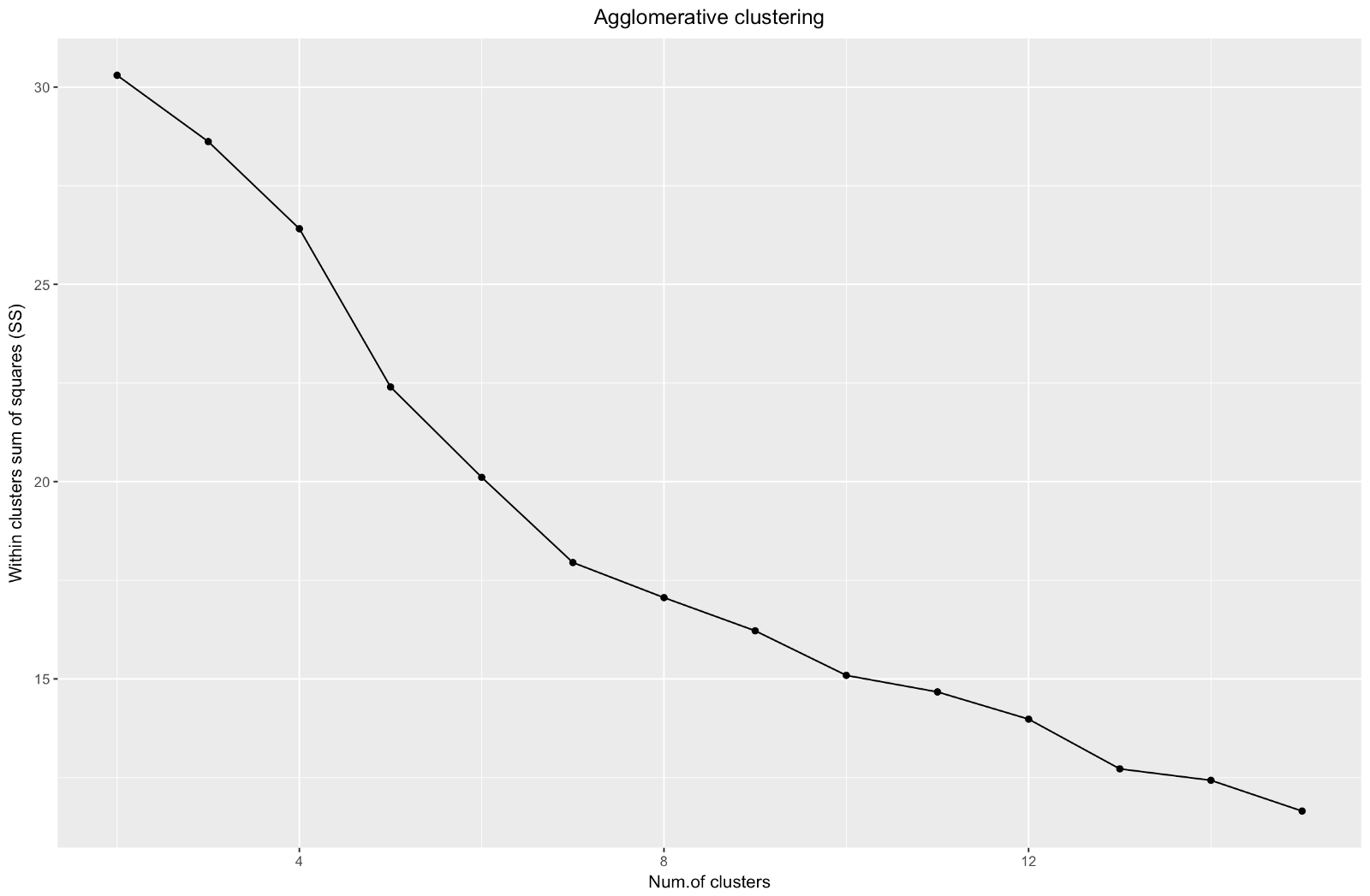
Агломеративный «локоть» похож на дивизионный, однако граф выглядит более плавным —?изгибы выражены не так резко. Как и при дивизионной кластеризации, я бы остановилась на 7 кластерах, однако при выборе между этими двумя методами размеры кластеров, которые получаются при агломеративном методе, мне нравятся больше —?лучше, чтобы они были сравнимыми друг с другом.
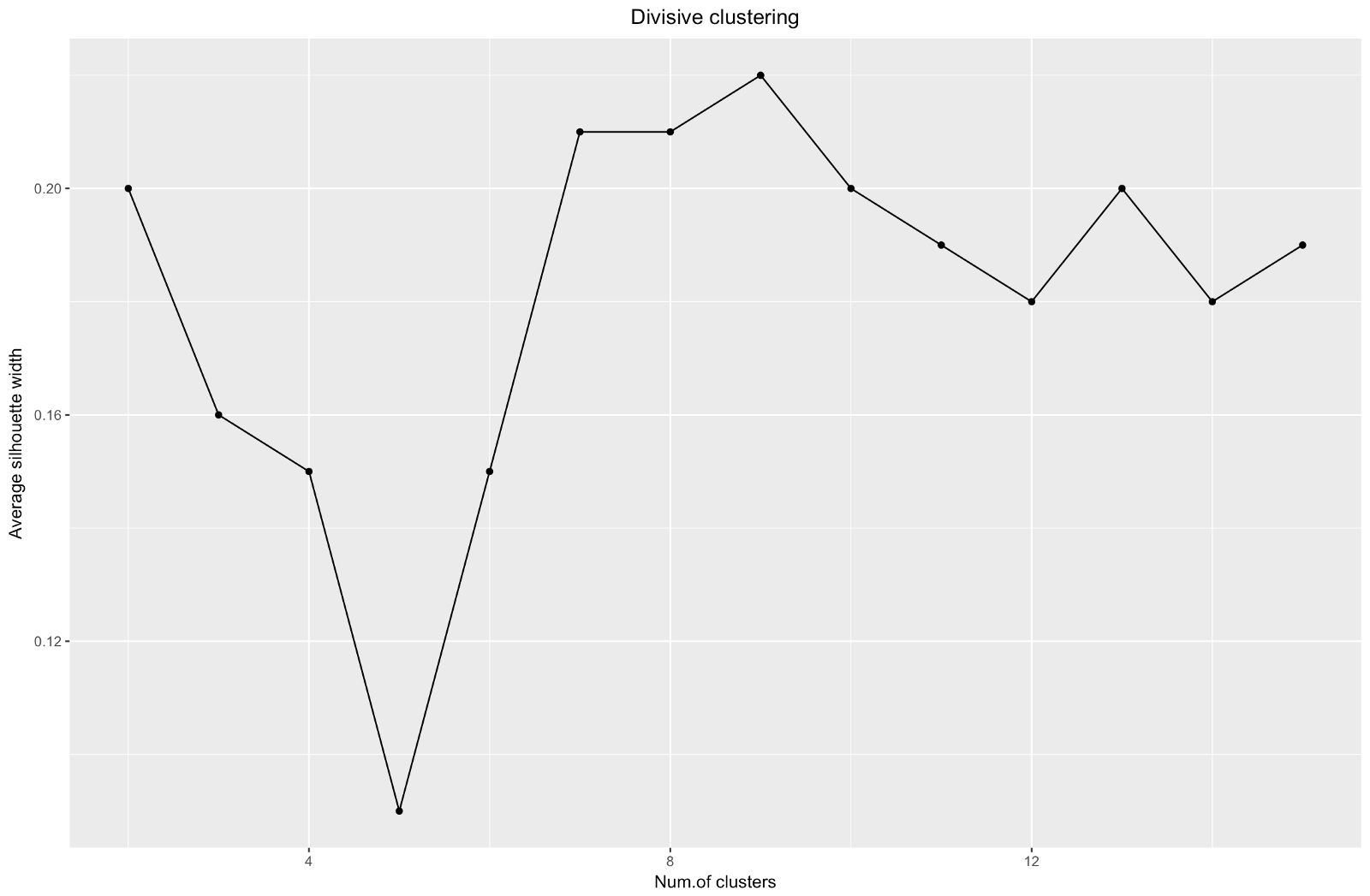
Когда используется метод оценки силуэтов, следует выбирать такое количество, которое дает максимальный коэффициент силуэта, потому что вам нужны кластеры, которые достаточно далеко отстоят от друга, чтобы считаться отдельными.
Коэффициент силуэта может составлять от –1 до 1, при этом 1 соответствует хорошей согласованности внутри кластеров, а –1 —?не очень хорошей.
В случае приведенного выше графика вы выбрали бы скорее 9, а не 5 кластеров.
Для сравнения: в «простом» случае график силуэтов похож на приведенный ниже. Не совсем как у нас, но почти.
Источник: Data Sailors
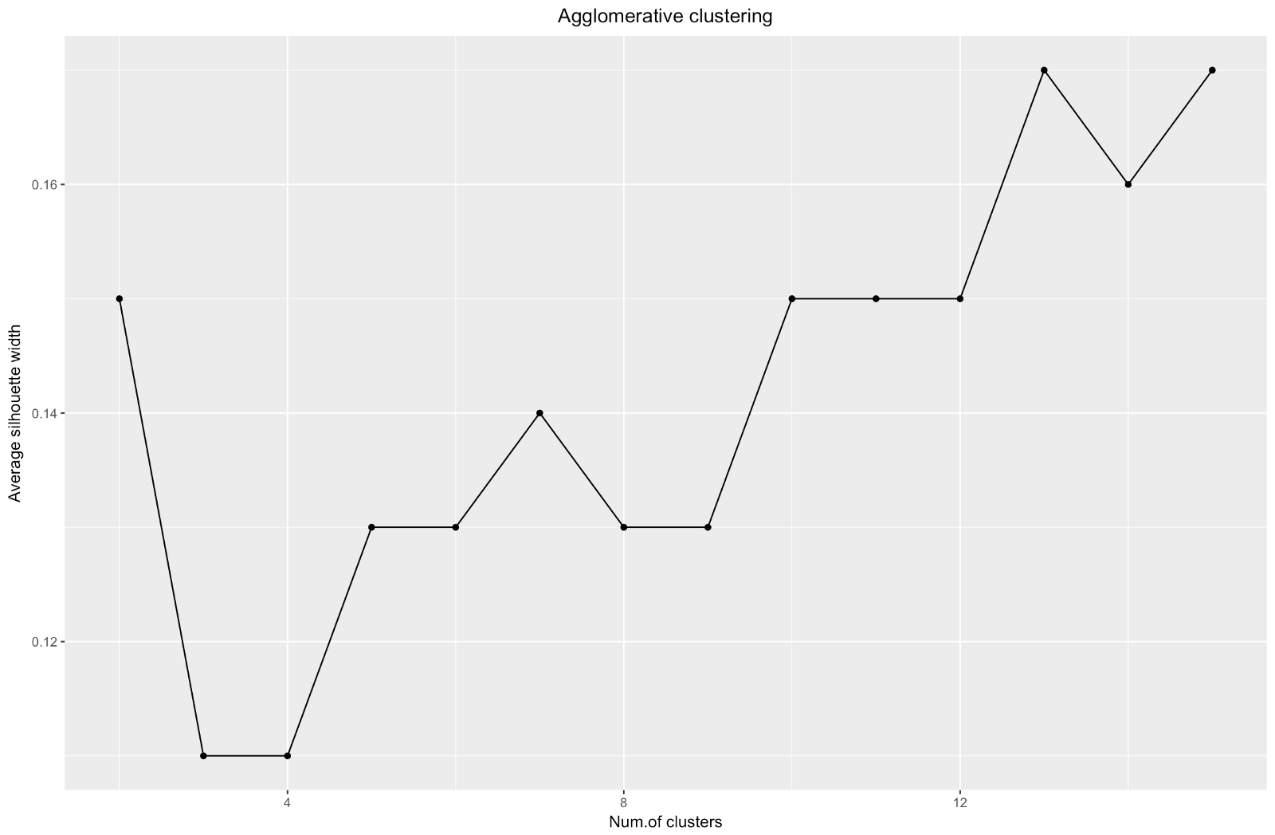
График ширины силуэтов говорит нам: чем сильнее вы разбиваете набор данных, тем более четкими становятся кластеры. Однако в конце концов вы дойдете до отдельных точек, а это вам не нужно. Однако именно это вы увидите, если начнете увеличивать количество кластеров k. Например, при
Подытожим: чем сильнее вы разбиваете набор данных, тем лучше кластеры, но мы не можем доходить до отдельных точек (например, на графике выше мы выделили 30 кластеров, а у нас всего 200 точек данных).
Итак, агломеративная кластеризация в нашем случае кажется мне гораздо более сбалансированной:?размеры кластеров более или менее сопоставимы (только взгляните на кластер всего из двух наблюдений при разделении дивизионным методом!), и я бы остановилась на 7 кластерах, полученных данным способом. Посмотрим, как они выглядят и из чего состоят.
Набор данных состоит из 6 переменных, которые нужно визуализировать в 2D или в 3D, так что придется потрудиться! Характер категориальных данных также накладывает некоторые ограничения, поэтому готовые решения могут не подойти. Мне нужно: а) видеть, каким образом наблюдения разбиты на кластеры, б) понимать, как наблюдения распределены по категориям. Поэтому я создала а) цветную дендрограмму, б) тепловую карту количества наблюдений на переменную внутри каждого кластера.

Тепловая карта наглядно показывает, сколько наблюдений приходится на каждый уровень фактора для исходных факторов (переменных, с которых мы начали). Темно-синий цвет соответствует относительно большому количеству наблюдений внутри кластера. Из этой тепловой карты также видно, что для дня недели (sun, sat… mon) и размера корзины (large, med, small) количество клиентов в каждой ячейке почти одинаково — это может означать, что данные категории не являются определяющими для анализа, и, возможно, их не нужно учитывать.
В этой статье мы рассчитали матрицу несходства, опробовали агломеративный и дивизионный методы иерархической кластеризации и ознакомились с методами «локтя» и силуэтов для оценки качества кластеров.
Дивизионная и агломеративная иерархическая кластеризация — неплохое начало для изучения темы, но не останавливайтесь на этом, если вы хотите по-настоящему овладеть кластерным анализом. Есть еще множество других методов и техник. Главным отличием от кластеризации численных данных является вычисление матрицы несходства. При оценке качества кластеризации не все стандартные методы будут давать надежные и осмысленные результаты —?метод силуэтов, весьма вероятно, не подойдет.
И наконец, поскольку уже прошло некоторое время с тех пор, как я сделала этот пример, сейчас я вижу ряд недостатков в своем подходе и буду рада любым отзывам. Одна из существенных проблем моего анализа не была связана с кластеризацией как таковой —?мой набор данных был несбалансирован по многим параметрам, и этот момент остался неучтенным. Это оказало заметное влияние на кластеризацию: 70 % клиентов относились к одному уровню фактора «гражданство», и эта группа доминировала в большинстве полученных кластеров, так что было трудно вычислить отличия внутри других уровней фактора. В следующий раз я попробую сбалансировать набор данных и сравнить результаты кластеризации. Но об этом — уже в другом посте.
Наконец, если вы хотите клонировать мой код, вот ссылка на github: https://github.com/khunreus/cluster-categorical
Надеюсь, что эта статья вам понравилась!
Руководство по иерархической кластеризации (подготовка данных, кластеризация, визуализация) — этот блог будет интересен тем, кто интересуется бизнес-аналитикой в среде R: http://uc-r.github.io/hc_clustering и https://uc-r.github.io/kmeans_clustering
Валидация кластеров: http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/
Пример категоризации документов (иерархической и методом k-средних): https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/
Очень интересный пакет denextend, позволяющий сравнить структуру кластеров при использовании разных методов: https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function
Существуют не только дендрограммы, но и кластерграммы: https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/
Сочетание тепловой карты и дендрограммы: https://jcoliver.github.io/learn-r/008-ggplot-dendrograms-and-heatmaps.html
Мне лично было бы интересно попробовать метод, представленный в статье https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ (репозиторий на GitHub: https://github.com/khunreus/EnsCat).

Это была моя первая попытка выполнить кластеризацию клиентов на основе реальных данных, и она дала мне ценный опыт. В Интернете есть множество статей о кластеризации с использованием численных переменных, однако найти решения для категориальных данных, работа с которыми несколько сложнее, оказалось не так просто. Методы кластеризации категориальных данных еще только разрабатываются, и в другом посте я собираюсь попробовать еще один.
С другой стороны, многие считают, что кластеризация категориальных данных может не давать вразумительных результатов —?и это отчасти верно (см. великолепное обсуждение на сайте CrossValidated). В какой-то момент я подумала: «Что я делаю? Их же можно просто разбить на когорты». Однако когортный анализ также не всегда целесообразен, особенно при значительном количестве категориальных переменных с большим числом уровней:?разобраться с 5–7 когортами можно без труда, но если у вас 22 переменные и у каждой по 5 уровней (например, опрос клиентов с дискретными оценками 1, 2, 3, 4 и 5), и нужно понять, с какими характерными группами клиентов вы имеете дело, —?у вас получится 22x5 когорт. С такой задачей никто не захочет возиться. И тут могла бы помочь кластеризация. Так что в этом посте я расскажу о том, что сама хотела бы узнать сразу, как только занялась кластеризацией.
Сам процесс кластеризации состоит из трех шагов:
- Построение матрицы несходства —?это, несомненно, самое важное решение при кластеризации. Все последующие шаги будут опираться на созданную вами матрицу несходства.
- Выбор метода кластеризации.
- Оценка кластеров.
Этот пост будет своеобразным введением, описывающим основные принципы кластеризации и ее реализацию в среде R.
Матрица несходства
Основой для кластеризации станет матрица несходства, которая в математических терминах описывает, насколько точки в наборе данных отличны (удалены) друг от друга. Она позволяет в дальнейшем объединить в группы те точки, которые находятся ближе всего друг к другу, или разделить наиболее удаленные друг от друга —?в чем и состоит основная идея кластеризации.
На этом этапе важны различия между типами данных, так как матрица несходства строится на основе расстояний между отдельными точками данных. Нетрудно представить себе расстояния между точками численных данных (известный пример — евклидовы расстояния), однако в случае категориальных данных (факторы в R) все не так очевидно.
Чтобы построить матрицу несходства в этом случае, следует использовать так называемое расстояние Говера. Я не буду углубляться в математическую часть этого понятия, просто приведу ссылки: вот и вот. Для этого я предпочитаю использовать
daisy() с метрикой metric = c("gower") из пакета cluster.#----- Фиктивные данные -----#
# данные будут максимально чистыми, чтобы не отвлекаться на возможные посторонние проблемы, но я опишу некоторые трудности, с которыми столкнулась, помимо написания кода
library(dplyr)
# обеспечение воспроизводимости для выборок
set.seed(40)
# создание случайного набора данных
# указание упорядоченных значений факторов; при использовании data.frame() строки преобразуются в факторы
# вначале идут идентификаторы клиентов, мы создаем 200 идентификаторов от 1 до 200
id.s <- c(1:200) %>%
factor()
budget.s <- sample(c("small", "med", "large"), 200, replace = T) %>%
factor(levels=c("small", "med", "large"),
ordered = TRUE)
origins.s <- sample(c("x", "y", "z"), 200, replace = T,
prob = c(0.7, 0.15, 0.15))
area.s <- sample(c("area1", "area2", "area3", "area4"), 200,
replace = T,
prob = c(0.3, 0.1, 0.5, 0.2))
source.s <- sample(c("facebook", "email", "link", "app"), 200,
replace = T,
prob = c(0.1,0.2, 0.3, 0.4))
## день недели — значения вероятности имитируют кривую спроса
dow.s <- sample(c("mon", "tue", "wed", "thu", "fri", "sat", "sun"), 200, replace = T,
prob = c(0.1, 0.1, 0.2, 0.2, 0.1, 0.1, 0.2)) %>%
factor(levels=c("mon", "tue", "wed", "thu", "fri", "sat", "sun"),
ordered = TRUE)
# блюдо
dish.s <- sample(c("delicious", "the one you don't like", "pizza"), 200, replace = T)
# по умолчанию data.frame() преобразует все строки в факторы
synthetic.customers <- data.frame(id.s, budget.s, origins.s, area.s, source.s, dow.s, dish.s)
#----- Матрица несходства -----#
library(cluster)
# для выполнения иерархической кластеризации разных типов
# использованные пакетные функции: daisy(), diana(), clusplot()
gower.dist <- daisy(synthetic.customers[ ,2:7], metric = c("gower"))
# class(gower.dist)
## несходство, расстояниеМатрица несходства готова. Для 200 наблюдений она строится быстро, но может потребовать очень большого объема вычислений, если вы имеете дело с большим набором данных.
На практике весьма вероятно, что сначала вам придется почистить набор данных, выполнить необходимые трансформации из строк в факторы и проследить за недостающими значениями. В моем случае набор данных также содержал строки отсутствующих значений, которые каждый раз красиво собирались в кластеры, так что казалось уже, что вот оно, сокровище, — пока я не посмотрела на значения (увы!).
Алгоритмы кластеризации
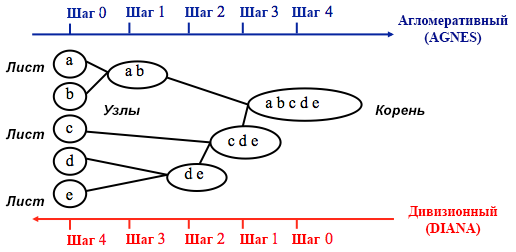
Возможно, вы уже знаете, что кластеризация бывает методом k-средних и иерархическая. В этом посте я фокусируюсь на втором методе, так как он более гибкий и допускает различные подходы: можно выбрать либо агломеративный (снизу вверх), либо дивизионный (сверху вниз) алгоритм кластеризации.

Источник: UC Business Analytics R Programming Guide
Агломеративная кластеризация начинается с
n кластеров, где n — число наблюдений: предполагается, что каждое из них представляет собой отдельный кластер. Затем алгоритм пытается найти и сгруппировать наиболее схожие между собой точки данных — так начинается формирование кластеров.Дивизионная кластеризация выполняется противоположным образом —?исходно предполагается, что все n точек данных, которые у нас есть, представляют собой один большой кластер, а далее наименее схожие из них разделяются на отдельные группы.
Принимая решение о том, какой из этих способов выбрать, всегда имеет смысл попробовать все варианты, однако в целом агломеративная кластеризация лучше подходит для выявления небольших кластеров и используется большинством компьютерных программ, а дивизионная кластеризация целесообразнее?для выявления крупных кластеров.
Лично я перед тем как решить, какой метод использовать, предпочитаю взглянуть на дендрограммы —?графическое представление кластеризации. Как вы увидите далее, некоторые дендрограммы хорошо сбалансированы, а другие — весьма хаотичны.
# Основные входные данные для кода ниже — несходство (матрица расстояний)
# После вычисления матрицы несходства дальнейшие шаги будут одинаковыми для данных всех типов
# Я предпочитаю сначала посмотреть на дендрограмму и выбрать самый привлекательный вариант — в данном случае мне был нужен самый сбалансированный — для последующей оценки
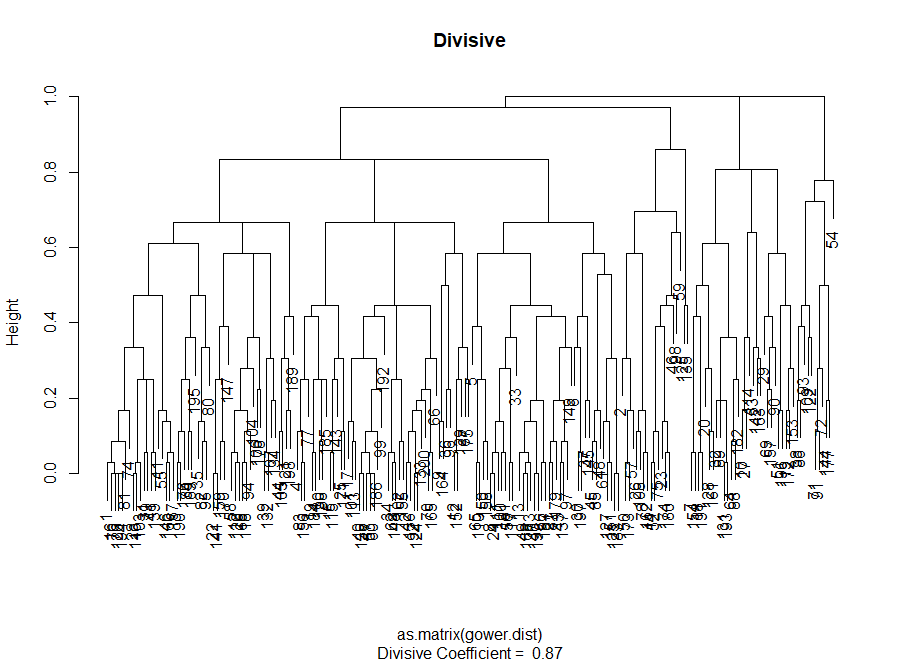
#------------ ДИВИЗИОННАЯ КЛАСТЕРИЗАЦИЯ------------#
divisive.clust <- diana(as.matrix(gower.dist),
diss = TRUE, keep.diss = TRUE)
plot(divisive.clust, main = "Divisive")
#------------ АГЛОМЕРАТИВНАЯ КЛАСТЕРИЗАЦИЯ ------------#
# Я ищу самый сбалансированный подход
# Этому запросу лучше всего соответствует метод полной связи — я оставлю здесь только его, чтобы не громоздить лишний код
# метод полной связи (complete linkages)
aggl.clust.c <- hclust(gower.dist, method = "complete")
plot(aggl.clust.c,
main = "Agglomerative, complete linkages")Оценка качества кластеризации
На этом этапе необходимо сделать выбор между различными алгоритмами кластеризации и различным количеством кластеров. Вы можете использовать разные способы оценки, не забывая руководствоваться здравым смыслом. Я выделила эти слова жирным шрифтом и курсивом, потому что осмысленность выбора очень важна —?количество кластеров и способ разделения данных на группы должны быть целесообразными с практической точки зрения. Число комбинаций значений категориальных переменных конечно (так как они дискретны), однако не любая разбивка на их основе будет осмысленной. Возможно, вы не захотите также, чтобы кластеров было очень мало —?в этом случае они будут слишком обобщенными. В итоге все зависит от вашей цели и задач выполняемого анализа.
В целом, при создании кластеров вы заинтересованы в получении четко выраженных групп точек данных, так, чтобы расстояние между такими точками внутри кластера (или компактность) было минимальным, а расстояние между группами (отделимость) — максимально возможным. Это легко понять интуитивно: расстояние между точками — это мера их несходства, полученная на основе матрицы несходства. Таким образом, оценка качества кластеризации опирается на оценку компактности и отделимости.
Далее я продемонстрирую два подхода и покажу, что один из них может давать бессмысленные результаты.
- Метод локтя: начните с него, если важнейшим фактором для вашего анализа является компактность кластеров, то есть сходство внутри групп.
- Метод оценки силуэтов: используемый в качестве меры согласованности данных график силуэтов показывает, насколько близко каждая из точек внутри одного кластера расположена к точкам в соседних кластерах.
На практике эти два метода часто дают разные результаты, что может привести к определенному замешательству — максимальная компактность и максимально четкое разделение будут достигаться при разном количестве кластеров, так что здравый смысл и понимание того, что на самом деле означают ваши данные, будут играть важную роль при принятии окончательного решения.
Есть также ряд метрик, которые вы можете проанализировать. Я добавлю их непосредственно в код.
# Статистика кластера выдается в виде списка, но удобнее рассматривать ее в виде таблицы
# Приведенный ниже код выдает кадр данных, где наблюдения расположены в столбцах, а переменные — в строках
# Это не идеально аккуратные данные, и над графическим представлением придется потрудиться, но я предпочитаю представить здесь результат в таком виде, так как считаю, что он более полный
library(fpc)
cstats.table <- function(dist, tree, k) {
clust.assess <- c("cluster.number","n","within.cluster.ss","average.within","average.between",
"wb.ratio","dunn2","avg.silwidth")
clust.size <- c("cluster.size")
stats.names <- c()
row.clust <- c()
output.stats <- matrix(ncol = k, nrow = length(clust.assess))
cluster.sizes <- matrix(ncol = k, nrow = k)
for(i in c(1:k)){
row.clust[i] <- paste("Cluster-", i, " size")
}
for(i in c(2:k)){
stats.names[i] <- paste("Test", i-1)
for(j in seq_along(clust.assess)){
output.stats[j, i] <- unlist(cluster.stats(d = dist, clustering = cutree(tree, k = i))[clust.assess])[j]
}
for(d in 1:k) {
cluster.sizes[d, i] <- unlist(cluster.stats(d = dist, clustering = cutree(tree, k = i))[clust.size])[d]
dim(cluster.sizes[d, i]) <- c(length(cluster.sizes[i]), 1)
cluster.sizes[d, i]
}
}
output.stats.df <- data.frame(output.stats)
cluster.sizes <- data.frame(cluster.sizes)
cluster.sizes[is.na(cluster.sizes)] <- 0
rows.all <- c(clust.assess, row.clust)
# rownames(output.stats.df) <- clust.assess
output <- rbind(output.stats.df, cluster.sizes)[ ,-1]
colnames(output) <- stats.names[2:k]
rownames(output) <- rows.all
is.num <- sapply(output, is.numeric)
output[is.num] <- lapply(output[is.num], round, 2)
output
}
# Я ограничиваю максимальное количество кластеров: их должно быть не больше 7
# Я хочу выбрать целесообразное количество, которое позволит мне в итоге выявить базовые различия между группами клиентов
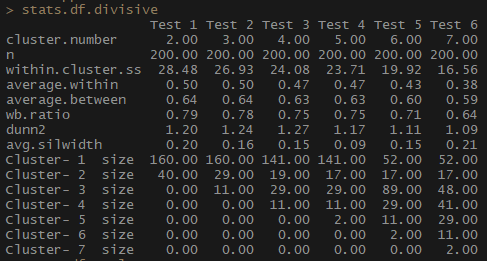
stats.df.divisive <- cstats.table(gower.dist, divisive.clust, 7)
stats.df.divisive
Итак, показатель average.within, который представляет среднее расстояние между наблюдениями внутри кластеров, уменьшается, как и within.cluster.ss (сумма квадратов расстояний между наблюдениями в кластере). Средняя ширина силуэта (avg.silwidth) меняется не так однозначно, однако обратную зависимость все же можно заметить.
Обратите внимание, насколько непропорциональны размеры кластеров. Я бы не стала торопиться работать с несравнимым количеством наблюдений внутри кластеров. Одна из причин состоит в том, что набор данных может быть несбалансированным, и какая-то группа наблюдений будет перевешивать при анализе все остальные —?это нехорошо и с большой вероятностью приведет к погрешностям.
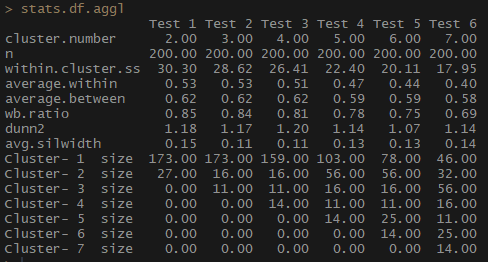
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #метод полной связи кажется наиболее сбалансированным подходомstats.df.aggl
Обратите внимание, насколько лучше сбалансирована по количеству наблюдений на группу агломеративная иерархическая кластеризация на основе метода полной связи.
# --------- Выбор количества кластеров ---------#
# Использование методов «локтя» и силуэта для определения количества кластеров
# чтобы яснее показать тенденцию, я попробую взять больше 7 кластеров
library(ggplot2)
# Локоть
# Дивизионная кластеризация
ggplot(data = data.frame(t(cstats.table(gower.dist, divisive.clust, 15))),
aes(x=cluster.number, y=within.cluster.ss)) +
geom_point()+
geom_line()+
ggtitle("Divisive clustering") +
labs(x = "Num.of clusters", y = "Within clusters sum of squares (SS)") +
theme(plot.title = element_text(hjust = 0.5))
Итак, мы создали график «локтя». Он показывает, как сумма квадратов расстояний между наблюдениями (мы используем ее как меру близости наблюдений — чем она меньше, тем ближе друг к другу измерения внутри кластера)?меняется для различного количества кластеров. В идеале мы должны увидеть отчетливый «локтевой сгиб» в той точке, где дальнейшее разбиение на кластеры дает лишь незначительное уменьшение суммы квадратов (SS). Для приведенного ниже графика я бы остановилась примерно на 7. Хотя в этом случае один из кластеров будет состоять всего из двух наблюдений. Посмотрим, что произойдет при агломеративной кластеризации.
# Агломеративная кластеризация дает менее ясную картину
ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))),
aes(x=cluster.number, y=within.cluster.ss)) +
geom_point()+
geom_line()+
ggtitle("Agglomerative clustering") +
labs(x = "Num.of clusters", y = "Within clusters sum of squares (SS)") +
theme(plot.title = element_text(hjust = 0.5))
Агломеративный «локоть» похож на дивизионный, однако граф выглядит более плавным —?изгибы выражены не так резко. Как и при дивизионной кластеризации, я бы остановилась на 7 кластерах, однако при выборе между этими двумя методами размеры кластеров, которые получаются при агломеративном методе, мне нравятся больше —?лучше, чтобы они были сравнимыми друг с другом.
# Силуэт
ggplot(data = data.frame(t(cstats.table(gower.dist, divisive.clust, 15))),
aes(x=cluster.number, y=avg.silwidth)) +
geom_point()+
geom_line()+
ggtitle("Divisive clustering") +
labs(x = "Num.of clusters", y = "Average silhouette width") +
theme(plot.title = element_text(hjust = 0.5))
Когда используется метод оценки силуэтов, следует выбирать такое количество, которое дает максимальный коэффициент силуэта, потому что вам нужны кластеры, которые достаточно далеко отстоят от друга, чтобы считаться отдельными.
Коэффициент силуэта может составлять от –1 до 1, при этом 1 соответствует хорошей согласованности внутри кластеров, а –1 —?не очень хорошей.
В случае приведенного выше графика вы выбрали бы скорее 9, а не 5 кластеров.
Для сравнения: в «простом» случае график силуэтов похож на приведенный ниже. Не совсем как у нас, но почти.

Источник: Data Sailors
ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))),
aes(x=cluster.number, y=avg.silwidth)) +
geom_point()+
geom_line()+
ggtitle("Agglomerative clustering") +
labs(x = "Num.of clusters", y = "Average silhouette width") +
theme(plot.title = element_text(hjust = 0.5))
График ширины силуэтов говорит нам: чем сильнее вы разбиваете набор данных, тем более четкими становятся кластеры. Однако в конце концов вы дойдете до отдельных точек, а это вам не нужно. Однако именно это вы увидите, если начнете увеличивать количество кластеров k. Например, при
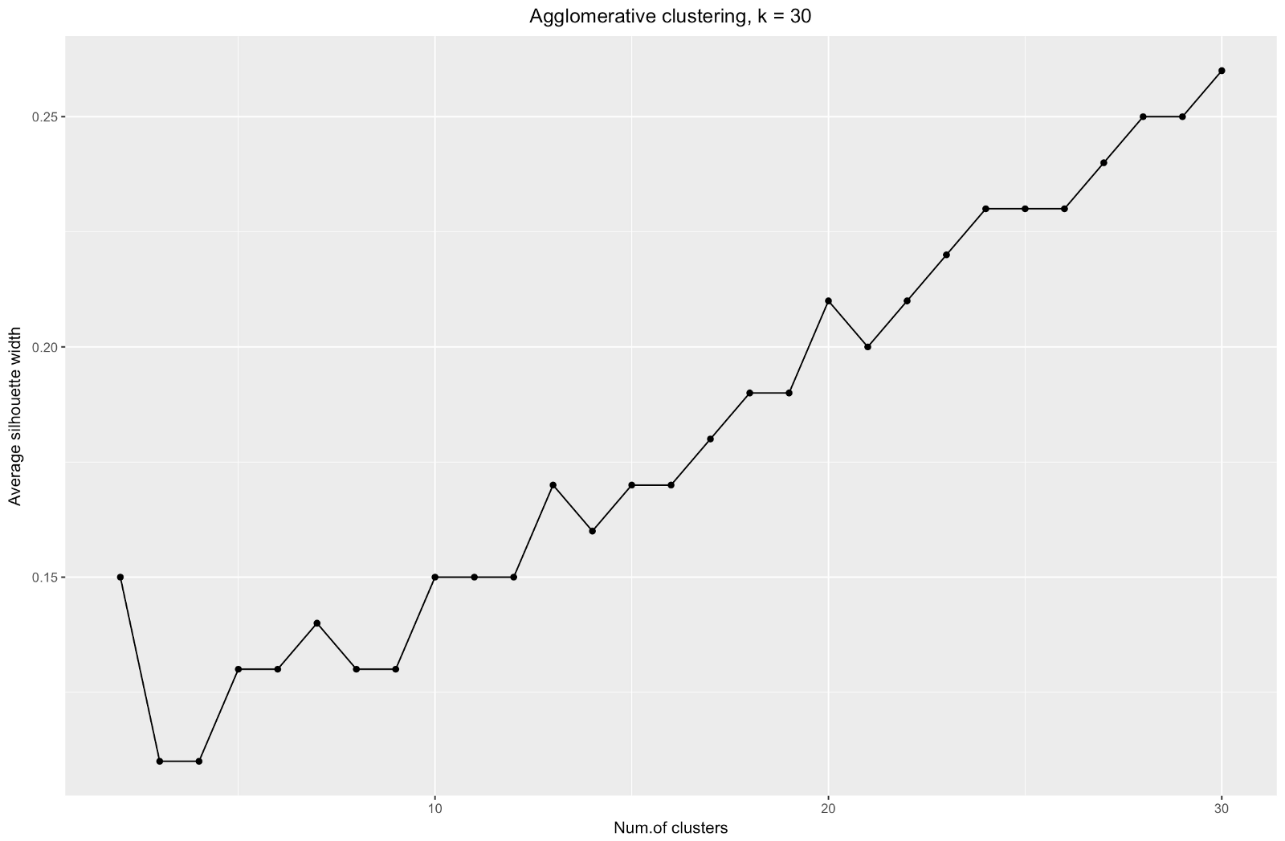
k=30 я получила следующий график:
Подытожим: чем сильнее вы разбиваете набор данных, тем лучше кластеры, но мы не можем доходить до отдельных точек (например, на графике выше мы выделили 30 кластеров, а у нас всего 200 точек данных).
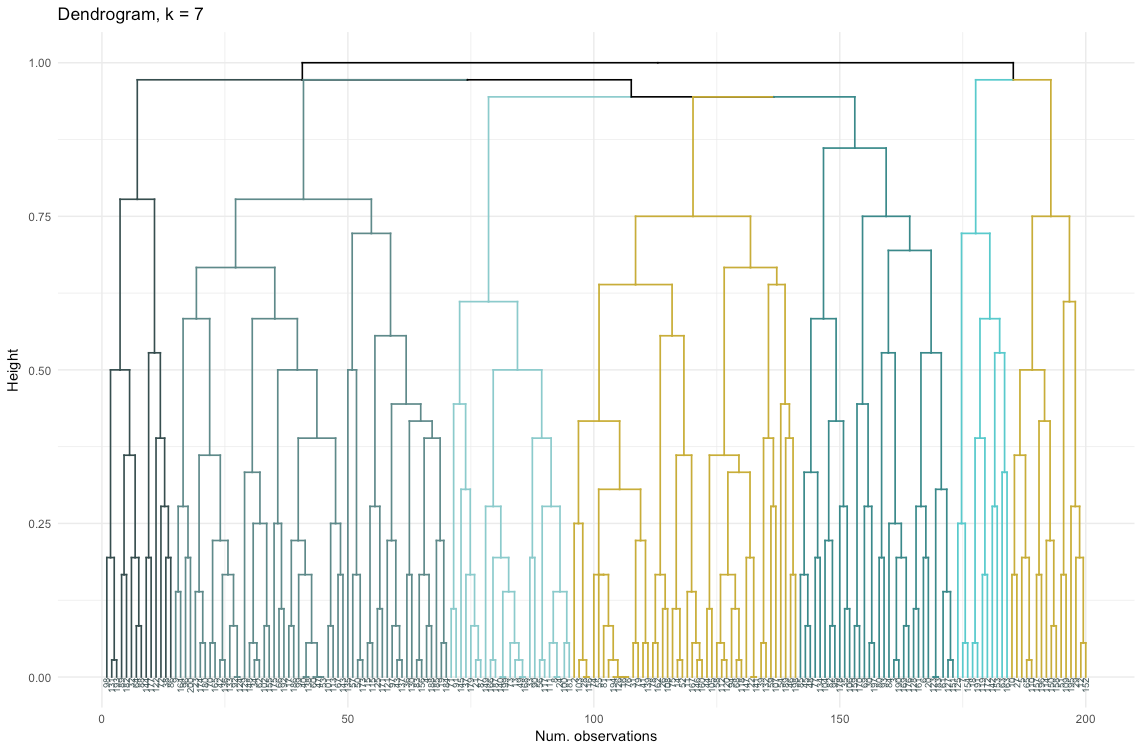
Итак, агломеративная кластеризация в нашем случае кажется мне гораздо более сбалансированной:?размеры кластеров более или менее сопоставимы (только взгляните на кластер всего из двух наблюдений при разделении дивизионным методом!), и я бы остановилась на 7 кластерах, полученных данным способом. Посмотрим, как они выглядят и из чего состоят.
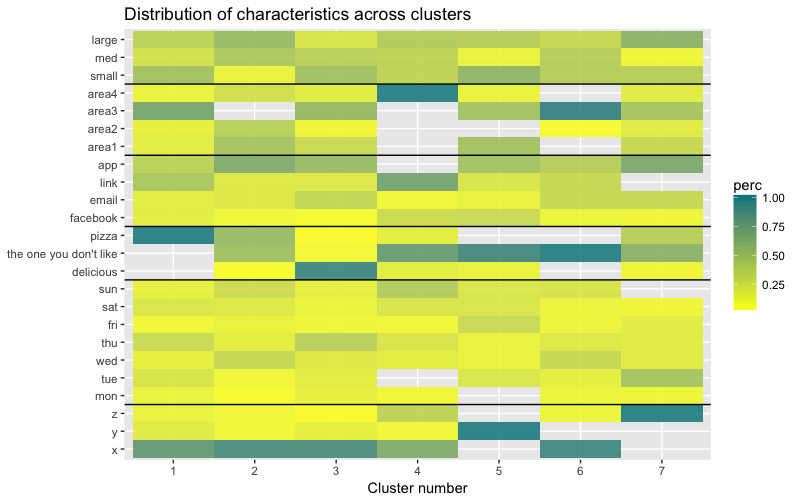
Набор данных состоит из 6 переменных, которые нужно визуализировать в 2D или в 3D, так что придется потрудиться! Характер категориальных данных также накладывает некоторые ограничения, поэтому готовые решения могут не подойти. Мне нужно: а) видеть, каким образом наблюдения разбиты на кластеры, б) понимать, как наблюдения распределены по категориям. Поэтому я создала а) цветную дендрограмму, б) тепловую карту количества наблюдений на переменную внутри каждого кластера.
library("ggplot2")
library("reshape2")
library("purrr")
library("dplyr")
# начнем с дендрограммы
library("dendextend")
dendro <- as.dendrogram(aggl.clust.c)
dendro.col <- dendro %>%
set("branches_k_color", k = 7, value = c("darkslategray", "darkslategray4", "darkslategray3", "gold3", "darkcyan", "cyan3", "gold3")) %>%
set("branches_lwd", 0.6) %>%
set("labels_colors",
value = c("darkslategray")) %>%
set("labels_cex", 0.5)
ggd1 <- as.ggdend(dendro.col)
ggplot(ggd1, theme = theme_minimal()) +
labs(x = "Num. observations", y = "Height", title = "Dendrogram, k = 7")
# Радиальная дендрограмма смотрится нагляднее (и круче)
ggplot(ggd1, labels = T) +
scale_y_reverse(expand = c(0.2, 0)) +
coord_polar(theta="x")
# Теперь — тепловая карта
# первый шаг здесь — выделить по строке для каждой переменной
# чтобы факторы не пропали, их следует преобразовать в символы
clust.num <- cutree(aggl.clust.c, k = 7)
synthetic.customers.cl <- cbind(synthetic.customers, clust.num)
cust.long <- melt(data.frame(lapply(synthetic.customers.cl, as.character), stringsAsFactors=FALSE),
id = c("id.s", "clust.num"), factorsAsStrings=T)
cust.long.q <- cust.long %>%
group_by(clust.num, variable, value) %>%
mutate(count = n_distinct(id.s)) %>%
distinct(clust.num, variable, value, count)
# heatmap.c подойдет, если вам требуются абсолютные количества — но, на мой вкус, это не очень информативно
heatmap.c <- ggplot(cust.long.q, aes(x = clust.num, y = factor(value, levels = c("x","y","z", "mon", "tue", "wed", "thu", "fri","sat","sun", "delicious", "the one you don't like", "pizza", "facebook", "email", "link", "app", "area1", "area2", "area3", "area4", "small", "med", "large"), ordered = T))) +
geom_tile(aes(fill = count))+
scale_fill_gradient2(low = "darkslategray1", mid = "yellow", high = "turquoise4")
# вычисление доли каждого уровня фактора в абсолютном количестве наблюдений в кластере
cust.long.p <- cust.long.q %>%
group_by(clust.num, variable) %>%
mutate(perc = count / sum(count)) %>%
arrange(clust.num)
heatmap.p <- ggplot(cust.long.p, aes(x = clust.num, y = factor(value, levels = c("x","y","z",
"mon", "tue", "wed", "thu", "fri","sat", "sun", "delicious", "the one you don't like", "pizza", "facebook", "email", "link", "app", "area1", "area2", "area3", "area4", "small", "med", "large"), ordered = T))) +
geom_tile(aes(fill = perc), alpha = 0.85)+
labs(title = "Distribution of characteristics across clusters", x = "Cluster number", y = NULL) +
geom_hline(yintercept = 3.5) +
geom_hline(yintercept = 10.5) +
geom_hline(yintercept = 13.5) +
geom_hline(yintercept = 17.5) +
geom_hline(yintercept = 21.5) +
scale_fill_gradient2(low = "darkslategray1", mid = "yellow", high = "turquoise4")
heatmap.p
Тепловая карта наглядно показывает, сколько наблюдений приходится на каждый уровень фактора для исходных факторов (переменных, с которых мы начали). Темно-синий цвет соответствует относительно большому количеству наблюдений внутри кластера. Из этой тепловой карты также видно, что для дня недели (sun, sat… mon) и размера корзины (large, med, small) количество клиентов в каждой ячейке почти одинаково — это может означать, что данные категории не являются определяющими для анализа, и, возможно, их не нужно учитывать.
Заключение
В этой статье мы рассчитали матрицу несходства, опробовали агломеративный и дивизионный методы иерархической кластеризации и ознакомились с методами «локтя» и силуэтов для оценки качества кластеров.
Дивизионная и агломеративная иерархическая кластеризация — неплохое начало для изучения темы, но не останавливайтесь на этом, если вы хотите по-настоящему овладеть кластерным анализом. Есть еще множество других методов и техник. Главным отличием от кластеризации численных данных является вычисление матрицы несходства. При оценке качества кластеризации не все стандартные методы будут давать надежные и осмысленные результаты —?метод силуэтов, весьма вероятно, не подойдет.
И наконец, поскольку уже прошло некоторое время с тех пор, как я сделала этот пример, сейчас я вижу ряд недостатков в своем подходе и буду рада любым отзывам. Одна из существенных проблем моего анализа не была связана с кластеризацией как таковой —?мой набор данных был несбалансирован по многим параметрам, и этот момент остался неучтенным. Это оказало заметное влияние на кластеризацию: 70 % клиентов относились к одному уровню фактора «гражданство», и эта группа доминировала в большинстве полученных кластеров, так что было трудно вычислить отличия внутри других уровней фактора. В следующий раз я попробую сбалансировать набор данных и сравнить результаты кластеризации. Но об этом — уже в другом посте.
Наконец, если вы хотите клонировать мой код, вот ссылка на github: https://github.com/khunreus/cluster-categorical
Надеюсь, что эта статья вам понравилась!
Источники, которые мне помогли:
Руководство по иерархической кластеризации (подготовка данных, кластеризация, визуализация) — этот блог будет интересен тем, кто интересуется бизнес-аналитикой в среде R: http://uc-r.github.io/hc_clustering и https://uc-r.github.io/kmeans_clustering
Валидация кластеров: http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/
Пример категоризации документов (иерархической и методом k-средних): https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/
Очень интересный пакет denextend, позволяющий сравнить структуру кластеров при использовании разных методов: https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function
Существуют не только дендрограммы, но и кластерграммы: https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/
Сочетание тепловой карты и дендрограммы: https://jcoliver.github.io/learn-r/008-ggplot-dendrograms-and-heatmaps.html
Мне лично было бы интересно попробовать метод, представленный в статье https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ (репозиторий на GitHub: https://github.com/khunreus/EnsCat).

