Содержание

Часть 1 — Задача двух тел

Трюкачество с заменой переменных

Приветствую всех! В прошлой части мы с вами получили уравнения движения системы из двух материальных точек, а также некоторую мотивацию на использование этой модели. Теперь же попробуем выжать как можно больше информации из них. Вот они:

\begin{equation*}
\begin{cases}
m_{1}\ddot{\vec{r}}_{1} = \vec{F}_{12}, (1)
\\
m_{2}\ddot{\vec{r}}_{2} = -\vec{F}_{12},
\end{cases}
\end{equation*}
где

$$

Система выглядит простой, особенно если закрыть глаза и не смотреть на выражение для $$. Даже, на мгновение, начинает казаться что уравнения линейные и решить её — тривиальное дело. Но куб всю малину портит, и если развернуть всё это дело и записать в фазовых координатах, то у нас задача нелинейная и вообще в 12-мерном пространстве (не поленился, набрал):

\begin{equation*}
\begin{cases}
\dot{x}_{1} = v_{1x}
\\
\dot{y}_{1} = v_{1y}
\\
\dot{z}_{1} = v_{1z}
\\
\dot{v}_{1x} = \dfrac{G m_{2}\left( x_{2} — x_{1} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }
\\
\dot{v}_{1y} = \dfrac{G m_{2}\left( y_{2} — y_{1} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }
\\
\dot{v}_{1z} = \dfrac{G m_{2}\left( z_{2} — z_{1} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }
\\

\dot{x}_{2} = v_{2x}
\\
\dot{y}_{2} = v_{2y}
\\
\dot{z}_{2} = v_{2z}
\\
\dot{v}_{2x} = \dfrac{G m_{1}\left( x_{1} — x_{2} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }
\\
\dot{v}_{2y} = \dfrac{G m_{1}\left( y_{1} — y_{2} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }
\\
\dot{v}_{2z} = \dfrac{G m_{1}\left( z_{1} — z_{2} \right)}{\left( \sqrt{(x_{2} — x_{1})^{2} + (y_{2} — y_{1})^{2} + (z_{2} — z_{1})^{2}} \right)^{3} }


\end{cases}
\end{equation*}

Если бы мы так сначала записали, то за этими деревьями леса не увидели, но Слава Богу, Он поднял нас на Свою гору Сион и с неё прекрасно видно весь лес целиком (кстати, если сейчас на Сибирь из космоса посмотреть, увидим что лес горит). И интуиция нам подскажет что делать с уравнениями 1. Эм, сложим и справа будет ноль:

$$

Ничего не напоминает? А так:

$$

Центр масс системы:

$$

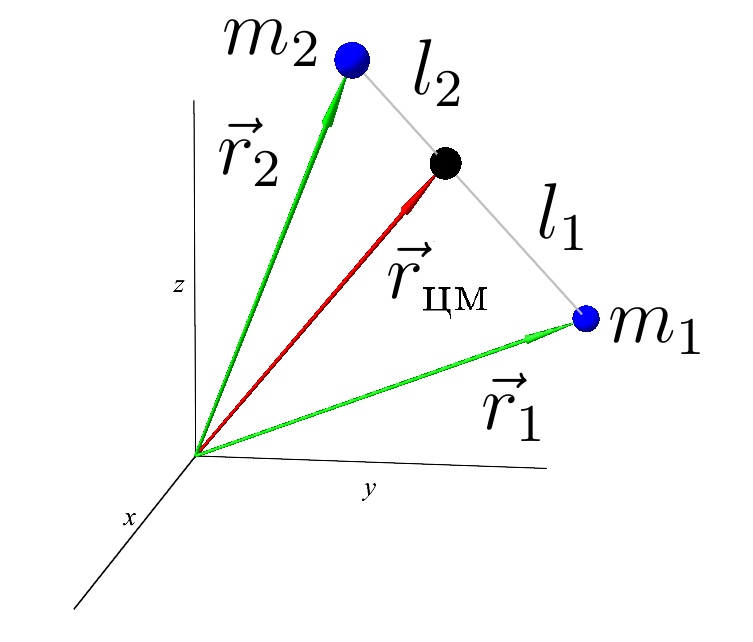
Центр масс двух тел. Отношения расстояний $$ и $$ равно отношению масс. Но в таком порядке, чтобы центр масс был ближе к более тяжелому телу.

а значит из 2 следует, что ускорение центра масс системы равно нулю:

$$

но это то же, что и первый закон Ньютона. Оказывается центр масс всегда и всюду будет двигаться прямолинейно с постоянной скоростью, либо оставаться на месте. Проинтегрируем 3 пару раз (здесь как бы система диффуров, но каждая координата интегрируется независимо от остальных):

$$

$$

где $$ — векторные константы, которые являются (анализированием размерностей) начальной скоростью и начальным положением центра масс соответственно. Ну так и перепишем:

$$

начальные условия пересчитать несложно:

$$

$$

а $$ — чтобы небыло недосказанности. Забыл в начале сказать, все эти начальные условия вместе с уравнениями 1 образуют задачу Коши, которая, как известно из раздела матана с диффурами, имеет чётко одно решение для каждого начального условия. А это хорошо, потому что бывают задачки посложнее, например, — краевые. Когда часть фазовых координат задается в одной точке, часть в другой точке. Бывает положение известно в начале, а скорость должна быть такой то в конце. А начальной скорости нет. И я чувствую, что такие задачки придется решать нам тоже, в будущем ;)

Можно даже проверить как центр масс движется, численно решив задачку. Старенький ноут, на котором я работаю, позволит это смоделировать:


Анимация движения тел и центра масс. Численное решение

Ну хорошо. Разобрались как двигается центр масс, но этого мало! Хочется узнать как тела двигаются. Еще разок взглянем на систему:

\begin{equation*}
\begin{cases}
m_{1}\ddot{\vec{r}}_{1} = G\dfrac{m_{1}m_{2}}{|\vec{r}_{2} — \vec{r}_{1}|^{3}}\left( \vec{r}_{2} — \vec{r}_{1}\right),
\\
m_{2}\ddot{\vec{r}}_{2} = -G\dfrac{m_{1}m_{2}}{|\vec{r}_{2} — \vec{r}_{1}|^{3}}\left( \vec{r}_{2} — \vec{r}_{1}\right),
\end{cases}
\end{equation*}
или
\begin{equation*}
\begin{cases}
\ddot{\vec{r}}_{1} = G\dfrac{m_{2}}{|\vec{r}_{2} — \vec{r}_{1}|^{3}}\left( \vec{r}_{2} — \vec{r}_{1}\right),
\\
\ddot{\vec{r}}_{2} = -G\dfrac{m_{1}}{|\vec{r}_{2} — \vec{r}_{1}|^{3}}\left( \vec{r}_{2} — \vec{r}_{1}\right),
\end{cases}
\end{equation*}
И там, и там справа разность $$ so let's do it quick:

$$

$$

ранее мы обозначили разность как $$ но теперь переобозначим $$ так как придется (скажу наперед) еще работать с этой штукой не раз. Ну всё, запомнили, и тогда последнее равенство примет вид:

$$

либо так:

$$

где $$ а $$ — относительное расстояние между телами. Начало вектора $$ в материальной точке номер 1, а конец в точке 2.



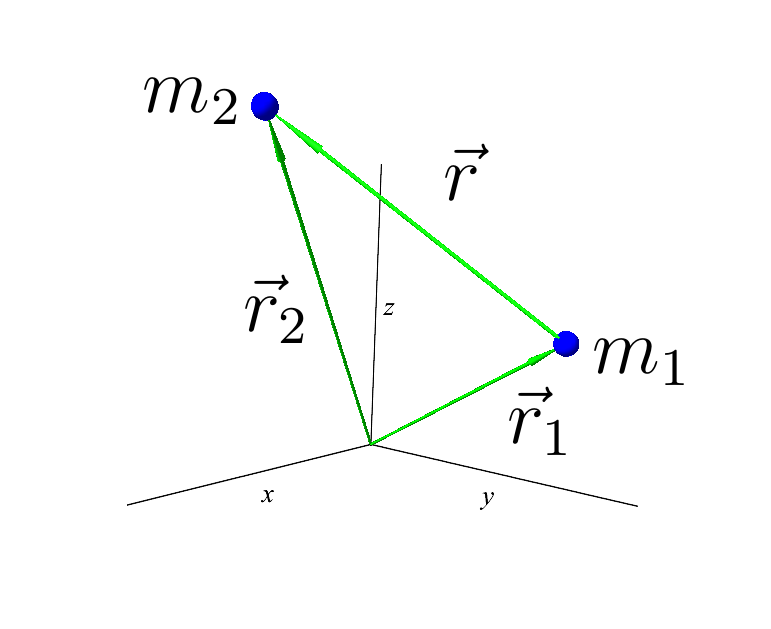
Вектор $$

По сути все эти трюки с центом масс и относительным расстоянием — линейное преобразование переменных:

\begin{equation*}
\begin{cases}
\vec{r}_{1} = \alpha_{1}\vec{r}_{\text{цм}} + \beta_{1}\vec{r},
\\
\vec{r}_{2} = \alpha_{2}\vec{r}_{\text{цм}} + \beta_{2}\vec{r},
\end{cases}
\end{equation*}
но пока что записано наоборот:

\begin{equation*}
\begin{cases}
\vec{r}_{\text{цм}} = \frac{m_{1}\vec{r}_{1} + m_{2}\vec{r}_{2}}{m_{1} + m_{2}},
\\
\vec{r} = \vec{r}_{2} — \vec{r}_{1},
\end{cases}
\end{equation*}
или
\begin{equation*}
\begin{cases}
\vec{r}_{\text{цм}} = \dfrac{m_{1}}{(m_{1} + m_{2})}\vec{r}_{1} + \dfrac{m_{2}}{(m_{1} + m_{2})}\vec{r}_{2},
\\
\vec{r} = — \vec{r}_{1} + \vec{r}_{2},
\end{cases}
\end{equation*}

можно и так:

$$

И теперь домножив на обратную матрицу слева (либо каким другим способом решить эту систему), можно выразить:

\begin{equation*}
\begin{cases}
\vec{r}_{1} = \vec{r}_{\text{цм}} — \dfrac{m_{2}}{m_{1} + m_{2}}\vec{r}, (5)
\\
\vec{r}_{2} = \vec{r}_{\text{цм}} + \dfrac{m_{1}}{m_{1} + m_{2}}\vec{r}.
\end{cases}
\end{equation*}

Это преобразование позволило нам разбить задачу на две независимые: отдельно найти движение центра масс и отдельно относительное расстояние. А через них уже выразить движение в глобальной системе координат. Так что пол задачи мы уже решили — как движется центр масс мы знаем. Теперь решив 4 задача будет считаться полностью решенной. Но это уже в следующий раз.

Сейчас же, еще следует добавить анализ уравнений 5. В случае, когда одно из тел будет намного массивнее другого (прим. Земля и Человек, или Земля и яблоко Человека). Примем первое тело массивным, второе — не очень: $$ или $$ что значит $$

В этом случае:

$$

— что означает сосредоточение центра масс системы прямо в массивном теле $$

\begin{equation*}
\begin{cases}
\vec{r}_{1} = \vec{r}_{\text{цм}} — \dfrac{1}{m_{1}}\dfrac{m_{2}}{1 + \dfrac{m_{2}}{m_{1}}}\vec{r} = \vec{r}_{\text{цм}} — \dfrac{m_{2}}{m_{1}}\dfrac{1}{1 + 0}\vec{r},
\\
\vec{r}_{2} = \vec{r}_{\text{цм}} + \dfrac{1}{m_{1}}\dfrac{m_{1}}{1 + \dfrac{m_{2}}{m_{1}}}\vec{r} = \vec{r}_{\text{цм}} + \dfrac{m_{1}}{m_{1}}\dfrac{1}{1 + 0}\vec{r}.
\end{cases}
\end{equation*}
Окончательно:
\begin{equation*}
\begin{cases}
\vec{r}_{1} = \vec{r}_{\text{цм}},
\\
\vec{r}_{2} = \vec{r}_{\text{цм}} + \vec{r}.
\end{cases}
\end{equation*}
Теперь, если перенести исходную систему координат в центр масс, получим:
\begin{equation*}
\begin{cases}
\vec{r}_{1} = 0,
\\
\vec{r}_{2} = \vec{r}.
\end{cases}
\end{equation*}
То бишь, мы связали новую координатную систему с Землей. И Земля в своей собственной коорд. системе неподвижна. Вектор $$ уже здесь является просто радиус вектором, но в то же время остается и относительным расстоянием между телами.

Так что в следующей статье, решая это уравнение:

$$

можно трактовать $$ как положение спутника в системе координат связанной с Землей например.
Хотя решив его, это совершенно необязательно. Решение будет для двух произвольных тел (произвольные массы).

Продолжение следует…

Литература:

Балк М.Б. Элементы динамики космического полета, М.: Наука, Глав.ред.физ.-мат.лит.,1965. — 338с.