
Конечно, можно быть успешным программистом и без сакрального знания структур данных, однако они совершенно незаменимы в некоторых приложениях. Например, когда нужно вычислить кратчайший путь между двумя точками на карте, или найти имя в телефонной книжке, содержащей, скажем, миллион записей. Не говоря уже о том, что структуры данных постоянно используются в спортивном программировании. Рассмотрим некоторые из них более подробно.
Очередь
Итак, поздоровайтесь с Лупи!

Лупи обожает играть в хоккей со своей семьей. И под “игрой”, я подразумеваю:

Когда черепашки залетают в ворота, их выбрасывает на верх стопки. Заметьте, первая черепашка, добавленная в стопку — первой ее покидает. Это называется Очередь. Так же, как и в тех очередях, что мы видим в повседневной жизни, первый добавленный в список элемент — первым его покидает. Еще эту структуру называют FIFO (First In First Out).
Как насчет операций вставки и удаления?
q = []
def insert(elem):
q.append(elem) #добавляем элемент в конец очереди
print q
def delete():
q.pop(0) #удаляем нулевой элемент из очереди
print q
Стек
После такой веселой игры в хоккей, Лупи делает для всех блинчики. Она кладет их в одну стопку.

Когда все блинчики готовы, Лупи подает их всей семье, один за одним.

Заметьте, что первый сделанный ею блинчик — будет подан последним. Это называется Стек. Последний элемент, добавленный в список — покинет его первым. Также эту структуру данных называют LIFO (Last In First Out).
Добавление и удаление элементов?
s = []
def push(elem): #Добавление элемента в стек - Пуш
s.append(elem)
print s
def customPop(): #удаление элемента из стека - Поп
s.pop(len(s)-1)
print s
Куча
Вы когда-нибудь видели башню плотности?
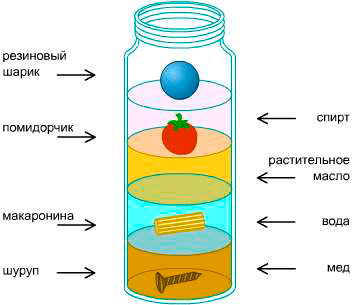
Все элементы сверху донизу расположились по своим местам, согласно их плотности. Что случится, если бросить внутрь новый объект?

Он займет место, в зависимости от своей плотности.
Примерно так работает Куча.
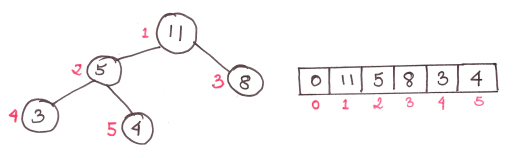
Куча — двоичное дерево. А это значит, что каждый родительский элемент имеет два дочерних. И хотя мы называем эту структуру данных кучей, но выражается она через обычный массив.
Также куча всегда имеет высоту logn, где n — количество элементов
На рисунке представлена куча типа max-heap, основанная на следующем правиле: дочерние элементы меньше родительского. Существуют также кучи min-heap, где дочерние элементы всегда больше родительского.
Несколько простых функций для работы с кучами:
global heap
global currSize
def parent(i): #Получить индекс родителя для i-того элемента
return i/2
def left(i): #Получить левый дочерний элемент от i-того
return 2*i
def right(i): #Получить правый дочерний элемент от i-того
return (2*i + 1)
Добавление элемента в существующую кучу
Для начала, мы добавляем элемент в самый низ кучи, т.е. в конец массива. Затем мы меняем его местами с родительским элементом до тех пор, пока он не встанет на свое место.

Алгоритм:
- Добавляем элемент в самый низ кучи.
- Сравниваем добавленный элемент с родительским; если порядок верный — останавливаемся.
- Если нет — меняем элементы местами, и возвращаемся к предыдущему пункту.
Код:
def swap(a, b): #меняем элемент с индексом a на элемент с индексом b
temp = heap[a]
heap[a] = heap[b]
heap[b] = temp
def insert(elem):
global currSize
index = len(heap)
heap.append(elem)
currSize += 1
par = parent(index)
flag = 0
while flag != 1:
if index == 1: #Дошли до корневого элемента
flag = 1
elif heap[par] > elem: #Если индекс корневого элемента больше индекса нашего элемента - наш элемент на своем месте
flag = 1
else: #Меняем местами родительский элемент с нашим
swap(par, index)
index = par
par = parent(index)
print heap
Максимальное количество проходов цикла while равно высоте дерева, или logn, следовательно, трудоемкость алгоритма — O(logn).
Извлечение максимального элемента кучи
Первый элемент в куче — всегда максимальный, так что мы просто удалим его (предварительно запомнив), и заменим самым нижним. Затем мы приведем кучу в правильный порядок, используя функцию:
maxHeapify().
Алгоритм:
- Заменить корневой элемент самым нижним.
- Сравнить новый корневой элемент с дочерними. Если они в правильном порядке — остановиться.
- Если нет — заменить корневой элемент на одного из дочерних (меньший для min-heap, больший для max-heap), и повторить шаг 2.
Код:
def extractMax():
global currSize
if currSize != 0:
maxElem = heap[1]
heap[1] = heap[currSize] #Заменяем корневой элемент - последним
heap.pop(currSize) #Удаляем последний элемент
currSize -= 1 #Уменьшаем размер кучи
maxHeapify(1)
return maxElem
def maxHeapify(index):
global currSize
lar = index
l = left(index)
r = right(index)
#Вычисляем, какой из дочерних элементов больше; если он больше родительского - меняем местами
if l <= currSize and heap[l] > heap[lar]:
lar = l
if r <= currSize and heap[r] > heap[lar]:
lar = r
if lar != index:
swap(index, lar)
maxHeapify(lar)
И вновь максимальное количество вызовов функции maxHeapify равно высоте дерева, или logn, а значит трудоемкость алгоритма — O(logn).
Делаем кучу из любого рандомного массива
Окей, есть два пути сделать это. Первый — поочередно вставлять каждый элемент в кучу. Это просто, но совершенно неэффективно. Трудоемкость алгоритма в этом случае будет O(nlogn), т.к. функция O(logn) будет выполняться n раз.
Более эффективный способ — применить функцию maxHeapify для ‘под-кучи’, от (currSize/2) до первого элемента.
Сложность получится O(n), и доказательство этого утверждения, к сожалению, выходит за рамки данной статьи. Просто поймите, что элементы, находящиеся в части кучи от currSize/2 до currSize, не имеют потомков, и большинство образованных таким образом ‘под-куч’ будут высотой меньше, чем logn.
Код:
def buildHeap():
global currSize
for i in range(currSize/2, 0, -1): #третий агрумент в range() - шаг перебора, в данном случае определяет направление.
print heap
maxHeapify(i)
currSize = len(heap)-1

Действительно, зачем это все?
Кучи нужны для реализации особого типа сортировки, называемого, как ни странно, “сортировка кучей”. В отличие от менее эффективных “сортировки вставками” и “сортировки пузырьком”, с их ужасной сложностью в O(n2), “сортировка кучей” имеет сложность O(nlogn).
Реализация до неприличия проста. Просто продолжайте последовательно извлекать из кучи максимальный (корневой) элемент, и записывайте его в массив, пока куча не опустеет.
Код:
def heapSort():
for i in range(1, len(heap)):
print heap
heap.insert(len(heap)-i, extractMax()) #вставляем максимальный элемент в конец массива
currSize = len(heap)-1
Чтобы обобщить все вышесказанное, я написала несколько строчек кода, содержащего функции для работы с кучей, а для фанатов ООП оформила все в виде класса.
Легко, не правда ли? А вот и празднующая Лупи!

Хеш
Лупи хочет научить своих детишек различать фигуры и цвета. Для этого она принесла домой огромное количество разноцветных фигур.
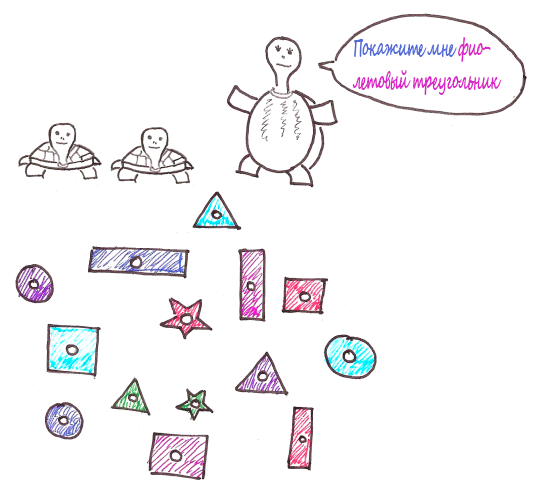
Через некоторое время черепашки окончательно запутались

Поэтому она достала еще одну игрушку, чтобы немного упростить процесс
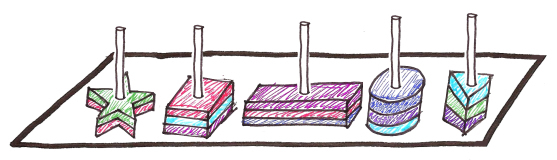
Стало намного легче, ведь черепашки уже знали, что фигуры рассортированы по форме. А что, если мы пометим каждый столб?

Черепашкам теперь нужно проверить столб с определенным номером, и выбрать из гораздо меньшего количества фигурок нужную. А если еще и для каждой комбинации формы и цвета у нас отдельный столб?
Допустим, номер столба вычисляется следующим образом:
Фиолетовый треугольник
ф+и+о+т+р+е = 22+10+16+20+18+6 = Столб 92
Красный прямоугольник
к+р+а+п+р+я = 12+18+1+17+18+33 = Столб 99
и.т.д.
Мы знаем, что 6*33 = 198 возможных комбинаций, значит нам нужно 198 столбов.
Назовем эту формулу для вычисления номера столба — Хеш-функцией.
Код:
def hashFunc(piece):
words = piece.split(" ") #разбиваем строку на слова
colour = words[0]
shape = words[1]
poleNum = 0
for i in range(0, 3):
poleNum += ord(colour[i]) - 96
poleNum += ord(shape[i]) - 96
return poleNum
(с кириллицей немного сложнее, но я оставил так для простоты. — прим.пер.)
Теперь, если нам нужно будет узнать, где хранится розовый квадрат, мы сможем вычислить:
hashFunc('розовый квадрат')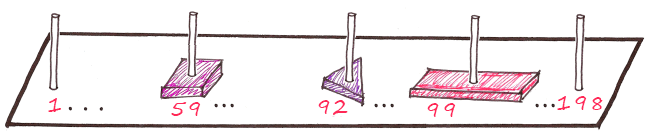
Это пример хеш-таблицы, где местоположение элементов определяется хеш-функцией.
При таком подходе время, затраченное на поиск любого элемента, не зависит от количества элементов, т.е. O(1). Другими словами, время поиска в хеш-таблице — константная величина.
Ладно, но допустим мы ищем “карамельный прямоугольник” (если, конечно, цвет “карамельный” существует).
hashFunc('карамельный прямоугольник')вернет нам 99, что совпадает с номером для красного прямоугольника. Это называется “Коллизия”. Для разрешения коллизии мы используем “Метод цепочек”, подразумевающий, что каждый столб хранит список, в котором мы ищем нужную нам запись.
Поэтому мы просто кладем карамельный прямоугольник на красный, и выбираем один из них, когда хеш-функция указывает на этот столб.
Ключ к хорошей хеш-таблице — выбрать подходящую хеш-функцию. Бесспорно, это самая важная вещь в создании хеш-таблицы, и люди тратят огромное количество времени на разработку качественных хеш-функций.
В хороших таблицах ни одна позиция не содержит более 2-3 элементов, в обратном случае, хеширование работает плохо, и нужно менять хеш-функцию.

Еще раз, поиск, не зависящий от количества элементов! Мы можем использовать хеш-таблицы для всего, что имеет гигантские размеры.
Хеш-таблицы также используются для поиска строк и подстрок в больших кусках текста, используя алгоритм Рабина-Карпа или алгоритм Кнута-Морриса-Пратта, что полезно, например, для определения плагиата в научных работах.
На этом, думаю, можно заканчивать. В будущем я планирую рассмотреть более сложные структуры данных, например Фибоначчиеву кучу и Дерево отрезков. Надеюсь, этот неформальный гайд получился интересным и полезным.
Переведено для Хабра запертым на чердаке программистом.
Комментарии (29)

conf
29.07.2015 09:51-4Спасибо за статью.
Чтобы обобщить все вышесказанное, я написала несколько строчек кода, содержащего функции для работы с кучей, а для фанатов ООП оформила все в виде класа
Во-первых, опечатка в словекласа
Во-вторых, ссылка вроде должна вести на код, оформленный в виде класса, но ведет на все тот же список функций.

Alexeyslav
29.07.2015 10:17+1Наконец-то узнал что такое куча. Всё остальное приходилось сталкиваться и использовать. Но кучи… применимость несколько ограничена.
Кстати не сказано еще что хеш-таблицы хоть и имеют малое время на поиск данных, но в компенсацию этой характеристики плохо работают на вставку/добавление новых записей посему имеют ограниченное применение.
khim
29.07.2015 11:35+11Куча — достаточно специфическая структура данных: у неё теоретически весьма неплохая сложность, но обращение к памяти весьма нерегулярное и потому она эффективна только на небольших размерах (когда она влазит в L1 кеш).
А насчёт «имеющих ограниченное применение» хеш-таблиц… вы это всерьёз или просто издеваетесь? В современном мире стоить только попытаться плюнуть — попадёшь в хеш-таблицу. Ещё до того, как плюнешь.
Когда вы пишите, скажем,
то куда, собственно, попадаетvar a = 1;a? Ответ: в хеш-таблицу соответствующей JavaScript-функции. А когда вы пишите
то вы оперируете, скорее всего, уже с тремя хеш-таблицами (одна — в которой хранитсяa.x = b.x;aиb, ещё два — живут внутри объектовaиb). То же самое — в большинстве других сколько-нибудь распространённых скриптовых языках (неважно: это python, ruby или какой-нибудь lisp). Даже такие языки как C++ и Java, в некотором смысле подвержены этой участи: у них тоже для каждой функции есть хеш-таблица с переменными… в компиляторе. Когда всё «замораживается» и получается скомпилированный код эти хеш-таблицы исчезают, но если вы используете какой-нибудь guice, то часть таблиц этого рода остаются и в рантайме.
С хеш-таблицами есть другая беда: если использовать некриптостойкий хеш, то можно на коллизии нарваться, а считать криптостойкие хеши долго. Слава богу тут нам пришёл на помощь Intel: на процессорах с поддержкой AES можно посчитать aeshash за то же время, что и какой-нибудь менее «замороченный» хеш, а DoS-атаку уже не провести.
Так что с хеш-таблицами всё хорошо: с вероятностью 99% вы их используете по 100 раз на дню, только не знаете об этом.
Alexeyslav
29.07.2015 14:28-4хеш-таблицы хороши когда соотношение чтение/запись сильно отличается, и когда нужно за один раз выбирать одно значение из таблицы. Большинство реальных запросов из баз данных и структур далеки от этих особенностей поскольку очень редко используют полный ключ для сопоставления записей, а для хеш-таблицы требуется исключительно полный ключ для позиционирования на конкретной записи, частичный ключ не имеет никакого смысла.
Единственное преимущество — это поиск конкретных записей по полному ключу в реально огромных базах данных, когда даже двоичный поиск в сортированном массиве не проходит по временным рамкам.
khim
29.07.2015 14:59+4Мы, в общем-то, говорим об одном и том же, только смотрим на проблему с разных сторон. Вы рассматриваете разные структуры с позиций «а чего, собственно, с ними можно сделать» и приходите к выводу, что хеш-таблицы ведь почти ничего делать-то и не умеют: «поиск конкретных записей по полному ключу» и только. Я же замечаю, что эта одна-единственная операция, собственно, и нужна чуть ли не в сто раз чаще, чем все остальные, вместе взятые и в результате вы, почти наверняка, используете кучу хеш-таблиц даже не замечая этого.
Единственное преимущество — это поиск конкретных записей по полному ключу в реально огромных базах данных, когда даже двоичный поиск в сортированном массиве не проходит по временным рамкам.
Ну да. Только я не знал что десяток элементов — это теперь называется «реально огромная база данных». Начиная примерно с этой точки хеш-таблицы начинают обгонять бинарный поиск — при условии, что хеш-функция распределяет данные по бакетам равномерно.MacIn
29.07.2015 23:35-2Вы всерьез не заметили, что человек сказал о куче, а не х. таблицах:
Всё остальное приходилось сталкиваться и использовать. Но кучи… применимость несколько ограничена.
?
khim
30.07.2015 01:10+1Неа. Я всерьёз заметил про что именно человек говорит:
Кстати не сказано еще что хеш-таблицы хоть и имеют малое время на поиск данных, но в компенсацию этой характеристики плохо работают на вставку/добавление новых записей посему имеют ограниченное применение.
MacIn
30.07.2015 01:42-1… и в ответе стали говорить о том, что таблицы применяются повсеместно, а не характеристиках вставки и удаления и связанных с этим ограничениями по применению, что было «ядром» высказывания. То, что хеш-таблицы применяются повсеместно (во многих областях) не вляется опровержением того, что у них есть ограничения (применение ограничено в силу характеристик). «Ограниченное применение» вовсе не означает, что структура мало где применяется.
Мне стоило написать не «Вы всерьез не заметили, что человек сказал о куче, а не х. таблицах», а "… не заметили, что человек сказал об ограниченности применения без уточнений именно о куче, а не хеш-таблицах..."
В первом сообщении сказано об ограниченном применении обоих структур, но «ограниченность» хеш-таблицы аргументирована, в отличие от кучи. Причем получается по сути трюизм — у каждой структуры есть особенности, которые ограничивают ее применение. Т.е. оспаривать фразу в целом бессмысленно — она верна в таком изложении (это трюизм), оспорить можно значимость характеристик вставки и пр., но не ссылкой на массовость применения. Указание же на ограниченность применения кучи — «голая», здесь нет аргументов, оправдывающих «ограниченность», и оспорить эту часть отсылкой к широте применения — разумный первый шаг.
khim
30.07.2015 02:08+1Вы тут развели какую-то философию вокруг пары фраз. Причём дурацкую. Я же отвечал по существу: куча — действительно довольно редко применяемая структура данных. Хотя обоснованием этого факта Alexeyslav действительно не озабачивался (да и непонятно как он мог озаботится если он о том как устроена эта структура узнал из этой статьи «для начинающих») — я это сделал за него.
Вторая же фраза является трюизмом только если у вас переклинило в голове и вы забыли о том, что в русском языке слова могут иметь несколько значений. Слово ограниченный — из их числа. Оно может обозначать как окруженный, отделенный, огороженный со всех сторон, так и небольшой, умеренный, имеющий достаточно узкие пределы. В первом варианте вся фраза становится трюизмом, который обсуждать бессмысленно, тут вы правы — но это, собственно, означает, что вы её неправильно поняли. Я и все остальные люди отметившиеся в теме обсуждали именно второй вариант прочтения этой фразы, вторую часть которой я и опроверг.
Обсуждать же «ядро» высказывания после этого уже не нужно: я опроверг следствие, а значит и посылка тоже неверна (вспоминаем уроки логики: из лжи может следовать как ложь, так и истина, но из истины ложь следовать никак не может).
P.S. Уж если хотите быть занудой — то хотя бы вчитывайтесь в то, что вы пишите. И не считайте всех кругом идиотами.MacIn
30.07.2015 13:47Вторая же фраза является трюизмом только если у вас переклинило в голове и вы забыли о том, что в русском языке слова могут иметь несколько значений
Именно об этом я вам и написал — о ином смысле слова «ограниченный», применимом в этом контексте.
Обсуждать же «ядро» высказывания после этого уже не нужно: я опроверг следствие
Только в случае, если воспринимать «ограниченность применения», как это сделали вы — как «редкий», «мало где применяющийся». Что, конечно, неверно. Опровержение следствия вида «хеш-таблицы используются повсюду, вы даже не замечаете этого» не опровергает посылки — посылка не была «мало где используется».
C «Я же замечаю, что эта одна-единственная операция, собственно, и нужна чуть ли не в сто раз чаще, чем все остальные, вместе взятые» не спорю.
P.S. Уж если хотите быть занудой — то хотя бы вчитывайтесь в то, что вы пишите. И не считайте всех кругом идиотами.
Что вы, это просто ремарка «проходя мимо» по поводу вашего разговора, не более. Никаких личных оценок; не воспринимайте это как выпад против вас. Вы правы по сути, и я с вами согласен в выводах. Просто претензия вида «хеш-таблицы, в силу своих особенностей (а и б) имеют ограниченное применение» разбивается простым «любая структура имеет ограничения в силу своих особенностей. Но операция поиска — наиболее частая и нагруженная, поэтому эти ограничения несущественны»(1). И это покрывает все смыслы «ограниченное применение». В отличие от «применяется повсюду»(2). (2) лишнее при наличии (1), я только об этом — по сути с вами согласен во всем.

boeing777
29.07.2015 12:13Про сортировку кучей стоит добавить, что она не требует дополнительной памяти и применима только к структурам данных с прямым доступом. И вообще, выбор метода сортировки должен производиться индивидуально под конкретную задачу. При малых размерах эффективнее могут оказаться qsort или сортировка Шелла.
И еще про применение кучи. Помимо сортировки, можно выполнять эффективный поиск элементов по определенному условию. Например, кроме банального максимума (который является корнем в max-heap), легко найти 2-й или 3-й по величине элемент — это будут непосредственные потомки корня, ну и так далее. Также куча применяется в алгоритмах на графах.
khim
29.07.2015 12:27+2Вы забыли про самое распространённое применение кучи: priority queue. Когда вам нужно выбрать N самых больших (или самых маленьких) элементов из множества, то куча — это самая подходящая структура. Обыно нужное N невелико, так что главный бич кучи (нелокальные обращения к памяти) не успевает проявиться, а зато тот факт, что не нужна дополнительная память (и, главное, что не нужно эту дополнительную память выделать и освобождать) оказывается весьма полезным.

nickolaym
29.07.2015 16:26Частичная сортировка по мотивам квиксорта тоже inplace делается.
en.cppreference.com/w/cpp/algorithm/nth_element
en.cppreference.com/w/cpp/algorithm/partial_sort
Причём, если нужно просто разбить N-элементный набор по K-ной порядковой статистике, то это выполняется за O(N). А если ещё и упорядочить первые K — то O(N*logK).
Хипсорт же — гарантировано выжрет O(N*logN) на построение кучи, а затем O(K*logN) на извлечение.
khim
29.07.2015 17:43+1Ну зачем же полный хипсорт-то делать? Достаточно маленькой кучки размера K. Легко и просто. Так у вас и памяти будет O(K) и времени потребуется O(N*logK). Первое — часто важнее, так как позволяет вам не портить обрабатываемые данные (если они в памяти) и обрабатывать данные, которые в память не влазят (в том числе распределённо на многих машинах). Что же касается K-ой порядковой статистики за время O(N), то сложность алгоритма (и, соответственно константа) там такие, что на небольших K (скажем до сотни) priority queue будет быстрее.

Avitella
29.07.2015 23:54Ничего подобного. www.cplusplus.com/reference/algorithm/nth_element
P.S. Сори (коменты не читай — сразу отвечай)

FlameStorm
04.08.2015 19:16> Например, кроме банального максимума (который является корнем в max-heap), легко найти 2-й или 3-й по величине элемент — это будут непосредственные потомки корня, ну и так далее. Также куча применяется в алгоритмах на графах.
Дабы читатели не остались в заблуждении, поправлю. 2й по величине элемент действительно находится в одном из двух потомков корня. А вот третий по величине элемент — это либо оставшийся потомок корня, либо один из двух потомков 2-го по величине элемента. Согласно определению кучи.
К слову, даже в той же википедии на иллюстрации-примере кучи 3-й по величине элемент находится не на первом, а на втором уровне глубины от корня.

dyadyaSerezha
29.07.2015 14:37+41. «Не говоря уже о том, что структуры данных постоянно используются в спортивном программировании.» — самый последний повод изучать структуры данных, на мой взгляд.
2. Черепашками по воротам? Куда смотрят защитники природы и комитет против пыток животных??
3. К тем же воротам — обычная очередь в магазине была бы гораздо более наглядной аналогией. Собственно, от человеческой очереди и пошло название этой структуры.

fshp
30.07.2015 05:04Хабрахабр — не для клонов.
Лучше бы от своего имени писали, а не создавали виртуала. С НЛО шутки плохи.
А за статью спасибо.

ultrabloxx
04.08.2015 13:11На рисунке представлена куча типа max-heap, основанная на следующем правиле: дочерние элементы меньше родительского. Существуют также кучи min-heap, где дочерние элементы всегда больше родительского.
На самом деле тут есть небольшая неточность, дочерние элементы в куче ещё могут быть равны родительскому элементу, иначе было бы неинтересно, а алгоритм пирамидальной сортировки требовал бы уникальности элементов массива.

radistao
04.08.2015 13:17Также куча всегда имеет высоту logn, где n — количество элементов
IMHO, в переводе на русский более привычно использоватьlog2 n


knagaev
Жаль, что не оставили в переводе оригинальное название “It’s turtles all the way down.” – A guide to the Basics of Data Structures
На самом деле это намёк на смешной случай с Бертраном Расселом.
А в целом отличный подход к знакомству со структурами данных для младшего поколения.
Или для старшего, которое ещё не наигралось.
Zveroloff
А что за случай? Не слышал.
knagaev
Этот случай, например, приведён в книге Хокинга «Кратчайшая история времени».
===
Несколько десятилетий назад известный ученый (некоторые говорят, что это был Бертран Рассел) выступал с публичной лекцией по астрономии.
Он рассказал, что Земля обращается вокруг Солнца, а оно, в свою очередь, — вокруг центра обширной звездной системы, называемой нашей Галактикой.
В конце лекции маленькая пожилая леди, сидевшая в задних рядах, встала и заявила:
— Вы рассказывали нам здесь полную ерунду. В действительности мир — это плоская плита, покоящаяся на спине гигантской черепахи.
Улыбнувшись с чувством превосходства, ученый спросил:
— А на чем стоит черепаха?
— Вы очень умный молодой человек, очень, — ответила старая леди. — Она стоит на другой черепахе, и так дальше, до бесконечности!
===
nickolaym
В более полной версии этой истории Рассел не просто рассказал о современной космологии, но перед этим обсмеял древнюю космологию с плоской землёй, китами-слонами и черепахой: мол, древние не задали себе вопрос, на чём же стоит та черепаха. А задали бы, так и отказались бы от неё.
Тут-то старушка взяла и поправила очень умного, но слишком молодого выскочку.