AntipovSN and MihhaCF

Часть вторая, в которой Атосу все норм, а вот Графу де ля Фер чего-то не хватает

Вступление от авторов:

Добрый день! Сегодня мы продолжаем цикл статей, посвященный скорингу и использованию в оном теории графов. С первой статьей Вы можете ознакомиться здесь.

Все шуточные аллегории, вставки и прочее призваны немного разгрузить повествование и не позволить ему свалиться в нудную лекцию. Всем, кому не зайдет наш юмор, заранее приносим извинения

Цель данной статьи: не более, чем за 30 минут, описать основные способы хранения данных о графах и описать правила и принципы построения нашей модели для скоринга заемщика.

Термины и определения:

• Хеш-таблица — это структура данных, реализующая интерфейс ассоциативного массива, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. Поиск по хеш-таблице, в среднем, осуществляется за время О(1).

Аудиторы, нанятые ПАО «Король» для оценки кредитоспособности НПАО «Один за всех», столкнулись с некоторыми проблемами. С одной стороны, описать схему взаимодействия 10-15 компаний и провести первичную оценку взаимодействия между компаниями очень просто, достаточно иметь под рукой лист бумаги и ручку. Но, что делать, если у вас имеется информация о взаимодействии десятков или сотен тысяч компаний? Например, если Вам нужно описать взаимодействия Арамиса со всеми его пассиями или Д’артаньяна со всеми, с кем он дрался?

Как хранить данные об этих взаимодействиях?

Какие структуры данных и подходы использовать?

Аудиторам пришлось бы сажать за эту работу целый монашеский корпус писунов.
Мы так делать не будем и наделим наших аудиторов знаниями и технологиями будущего (отправим к ним Прометея в виде Т-800, который даст им свет знаний).

Ну, что ж, начнем отвечать на поставленные вопросы. Да будет свет!

Как мы уже писали и рисовали здесь, граф – это отношение 2-х множеств – множества узлов и множества ребер. Как же лучше хранить граф?

Прежде чем ответить на вопрос как хранить граф, нужно решить, а что конкретно мы хотим хранить и в каком виде.

По теории графов узлами графа могут быть любые объекты с любым набором параметров (этот факт пригодится нам позже, для продвинутых/адаптивных моделей расчета скорингового бала).

Так что же нам нужно хранить?

Как минимум, идентификатор узла и идентификаторы его соседей (с кем связан). Наличие этих данных уже позволяет осуществлять поиск в ширину и глубину.

Нужно ли хранить данные о ребрах графа? Да, если мы имеем дело со взвешенным графом. В нашем случае, мы имеем дело со взвешенным графом и в первой статье мы нарисовали именно такой граф.

Достаточно ли этой информации? Нет.

Откуда взялись веса у ребер? В учебниках эта информация просто есть, кто-то ее собрал и обработал до нас. В нашем же позднем средневековье (именно тогда жили мушкетеры) никто не озаботился подсчетом весов ребер нашего графа. Мы должны сделать это сами. В этой и следующей статье мы не будем расписывать конкретную методику расчета веса ребра, это будет сделано в 4 статье. Сейчас нам важно определиться какую информацию о нашем графе мы будем хранить.

Итак, в нашем случае, есть три ключевых параметра, которые мы должны знать для корректного расчета скорингового балла:

• Внутреннюю оценку узла – складывается из показателей, характеризующих узел (оборот, задолженности, штрафы и пр). В нашем примере это будут:
  
  • Оценка — хороший или плохой узел по отношению к НПАО «Один за всех»;
  • Ранг узла – Король имеет наивысший ранг, Бонасье – наименьший;
  • Объем фондов, проще говоря, состоятельность.
• Оценку ребра. В нашем случае оценка связи будет для каждого узла – это значит, что связь Бонасье – Констанция может не равняться связи Констанция – Бонасье, т.к. они имеют разные возможности влияния друг на друга.
• Уровень узла – храниться не будет, но является важным показателем.

Не спрашивайте откуда взялись в модели все эти числа, Д’артаньян так видит. В реальной жизни эти показатели будут рассчитываться тоже не нами (торговый оборот, долги, штрафы и пр. мы берем из уже существующих источников, мы ж не в средневековье, вроде).

Из всего вышеперечисленного получается, что мы должны хранить помимо идентификаторов узлов, параметры каждого узла и веса ребер, которые мы получаем на основании агрегации параметров узлов.

Итого, хранению подлежит следующая информация:

• Название узла;
• Параметры узла;
• Соседи узла;
• Вес ребра для каждого соседа.

Отлично! Разобрались, что нам нужно хранить. Теперь — как хранить.

И опять небольшое отступление.

Как будет выглядеть наш процесс скоринга в упрощенном виде:

• Сбор данных об объекте;
• Формирование объекта, который будет описывать модель графа. Именно на этом объекте мы будем проводить все наши операции скоринга.

Исходя из этих двух этапов у нас есть три варианта:

• Храним данные об объекте скоринга на SQL / NoSQL сервере. Все операции, связанные с расчетами, алгоритмами и пр. проводим непосредственно на сервере;
• Храним данные об объекте скоринга на SQL / NoSQL сервере. На основании этих данных создаем отдельный объект (например, хеш-таблицу), с которой проводим все основные вычисления;
• Данные об объекте скоринга храним в оперативной памяти. На основании этих данных создаем отдельный объект (например, хеш-таблицу), с которой проводим все основные вычисления.

Основные требования к данному процессу:

• Скорость работы;
• Надежность;
• Верифицируемость.
  Теперь давайте рассуждать. Сядем, как наши мушкетеры за кружечкой чего они там пили, чая, например. Главное, чтобы нам не мешали всякие петухи с гвардейцами.

Если нужно долговременное хранение, то можно выбрать таблицу, с соответствующими значимыми полями. В NoSQL или оперативной памяти лучше хранить данные в виде списка или справочника (хеш-таблица) объектов.

{ 'Id': 1, 'Title': 'НПАО Один за всех', 'Rang': 4, 'Type': 'НПАО', 'Profit': 10000 }

С вершинами более-менее понятно. Как же лучше представить дуги/ребра графа? Для этого нужно понимать основной принцип любых аналитических операций над графом – обращение к любой дуге/ребру должно происходить очень быстро, желательно, чтобы время обращения было равно O(1). Сразу в голову приходить массив или матрица – структура, в которой к любому элементу можно обратиться быстро по индексу.

[i,j] – элемент матрицы обозначает дугу графа, где i- идентификатор начальной вершины, j — идентификатор конечной вершины, обращение и выбор начальной вершины происходит непосредственно по идентификатору начальной вершины. Пересечение i и j хранит вес ребра.

В таком представлении есть несколько минусов:

• Часто структура бывает избыточна, особенно, если граф разреженный (малое количество ребер), много пустых значений, которые обозначают, что связи нет.
• Для нахождения всех соседей вершины нужно перебрать массив всех элементов i-той строки матрицы отношений.
• Матрицу с многими столбцами не сохранить в БД.

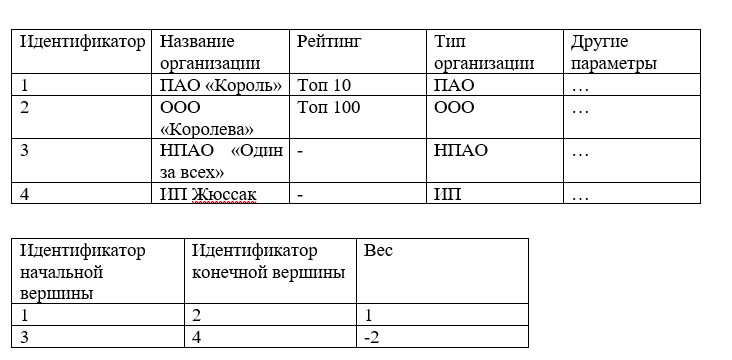
Следующий вариант хранения дуг/ребер – таблица, то есть набор столбцов и строк.
Например:

Такую структуру можно легко сохранить в реляционной БД и при выполнении SQL запросов выбирать нужные значения, но, когда речь идет об оперативной памяти, сложность поиска всех ребер вершины увеличивается и в общем случае занимает O(n) где n количество всех ребер графа.

Существует еще один очень хороший метод хранения графа для использования практически во всех системах, лишенный недостатков, описанных выше — это справочник ключ-значение или хеш-таблица. Получение всех ребер нужной вершины происходит с O(1) скоростью.
Существенный минус, что не все языки программирования поддерживают такую конструкцию.

Как же можно представить подобную структуру в разных системах?

В реляционной базе можно реализовать связь таблиц объектов и ребер (предыдущий пункт)

NoSQL

{ 'Id': 1, 'Title': 'НПАО Один за всех', 'Rang': 4, 'Type': 'НПАО', 'Profit': 10000, 'Relations': [{3,2}, {4,5}, … {n, -5}] }

При обращении к объекту по его ключу, сразу получаем набор его связей. Если у нас невзвешенный граф, вместо массива объектов можно передать массив идентификаторов соседей Relations: [3,4, … n]. В виде справочника ключ – значение, такой вариант похож на предыдущий. В справочнике ключ – значение можно хранить такой же объект, как в предыдущем примере, ключом, конечно, будет являться идентификатор вершины (может быть число, может быть строка и т.д., что позволяет конкретная системы разработки). Так же в справочнике можно хранить только массивы связей, а информацию о вершинах в другом справочнике.

Graf[1] = { 'Id': 1, 'Title': 'НПАО Один за всех', 'Rang': 4, 'Type': 'НПАО', 'Profit': 10000, 'Relations': [{3,2}, {4,5}, … {n, -5}] } 

или

graf['one_for_all'] = 'Relations': [{3,2}, {4,5}, … {n, -5}]

Для нашего примера мы выбрали вариант хранения данных в оперативной памяти с созданием хеш-таблицы для скоринга данных. Промежуточные результаты будем записывать в файл на сервере.

Со структурами хранения худо – бедно определились, теперь пришло время разобраться, с чего начать построение нашей аналитической модели. Начнем с простого- определим взаимодействие с ближайшими соседями и с соседями соседей (друзья друзей).

Таким образом можно определить взаимодействие со всем связанными между собой вершинами. По нашим наблюдениям взаимодействие с соседями глубже 2 уровня представляет интерес только в особенных случаях и рассчитывается по другим методикам. Сложность этого расчета довольно велика 0(2^n).

Для расчета бала мы будем использовать немного измененный алгоритм поиска в глубину.

Доработка будет заключаться в следующем:

1. Нужно найти не конкретную вершину, а перебрать все вершины на глубину n, для нашей задачи n=2.
2. Мы не должны хранить лишнюю информацию и должны предполагать, что расчет может производиться для любого узла графа, поэтому уровень узла храниться в графе не будет.
3. Если в вершину ведут 2 и более путей, то оцениваются все пути, т.к. мы имеем дело с двунаправленными связями и необходимо максимально полно оценить взаимодействия узлов.
4. Нужно иметь возможность определять уровень вложенности любой вершины для конкретного расчета.

Ну, что ж, основные теоретические выкладки сделаны, пусть они и покажутся кому-то чем-то простым и банальным. Но для нас, гасконцев, это все важно и интересно, почти так же, как поступление в Королевские мушкетеры.

Переходим к практической реализации. Один за всех и все на одного!

Встретимся! Мы обязательно встретимся! Может быть через 10 лет или 20! Но встретимся!

Следующая статья близко!