Схема отбора в выборку — это детальное описание того, какие данные и каким способом будут получены. Есть много схем для отбора в выборку, поэтому нужно выбрать для исследований такую, которая даст наиболее репрезентативные результаты. Репрезентативность выборки — это соответствие характеристик выборки характеристикам популяции.
В идеале лучше работать со всей генеральной совокупностью, но это занимает много времени и ресурсов. Поэтому можно исследовать только ее часть, что и называется выборкой. Затем исследуются элементы, которые попали в выборку. На основе полученных значений оцениваются неизвестные элементы выборки.

Идея состоит в том, чтобы перенести результаты на всю генеральную совокупность. Поэтому выборка должна быть репрезентативной. Другими словами она пропорциональна как подгруппам, так и всей совокупности, и не исключает каких-либо отдельных групп.
Выборка должна быть настолько большой, насколько это возможно, чтобы избежать ошибочных суждений. По сути выборкой может быть любое подмножество генеральной совокупности.
Если выборка недостаточно репрезентативна — исследование будет считаться предвзятым. Если она будет недостаточно большой — неточным.
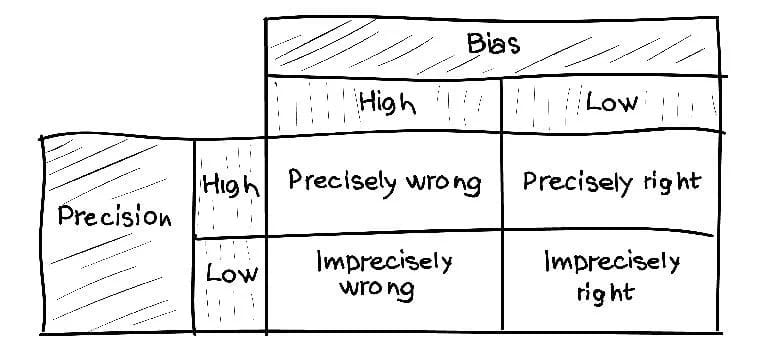
Если правильно подобрать связь между выборкой и совокупностью, тогда можно сделать правильные заключения о природе всей совокупности. Лучше быть возможно правым, чем точно не правым.
Вероятностные выборки подразумевают, что исследователь абсолютно уверен в связях выборки с генеральной совокупностью. Если же связи не прослеживаются или в наличии имеются не все элементы генеральной совокупности используется невероятностная выборка.
Схема отбора состоит в том, чтобы провести ряд испытаний без возвращения элемента в генеральную совокупность. Каждый элемент совокупности имеет одинаковые шансы попасть в выборку.
Из генеральной совокупности N случайным образом отбирается один элемент, вероятность попадания элемента в выборку равна 1/N. Затем из выборки N-1 выбирается второй элемент с вероятностью 1/(N-1) и так далее до n-го элемента с вероятностью 1/(N-n).
Отбор происходит из упорядоченного списка из N элементов. Пусть наперед задано некоторое число ? (1<?<0) и набор N независимых реализаций равномерно распределенной на [0,1] случайной величины ?1…?N. Каждому элементу k ставится в соответствие значение. Если ?к<?, то этот элемент отбирается, в другом случае — нет. Возможность того, что элемент будет выбран равна ? для каждого из N элементов. Таким образом каждый элемент, который попал в выборку является биномиально распределенной величиной.
Пусть N — размер генеральной совокупности. а — некоторое фиксированное число. а ? N. Первый элемент выборки выбирается случайным образом среди первых a элементов совокупности. Выбранное число r 1? r ?a называется случайным стартом (началом), а число а — выборочным интервалом. Каждый элемент [1,2… а] имеет одинаковую вероятность быть выбранным, равную 1/а. Далее в выборку попадают элементы с шагом а.
Можно получить а разных выборок, каждая из которых имеет одинаковую вероятность быть выбранной.
Во всех вышеизложенных схемах у элемента не было возможности попасть в выборку более 1 раза.
Это логично, так как при повторном включении элемента новая информация не добавляется. Но в этом случае некоторые оценки имеют очень простые статистические свойства, что дает возможность исследовать довольно сложные процедуры отбора.
Например, выполняется m независимых отборов элементов из генеральной совокупности размера N с одинаковыми вероятностями 1/N. Отобранный элемент возвращается в совокупность. Таким образом все N элементов участвуют в отборе постоянно.
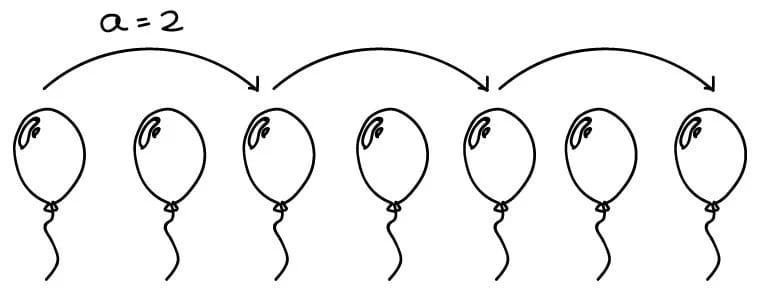
Предполагает, что все числа генеральной совокупности должны быть хорошо перемешаны. Тогда исследователь берет каждый а-й элемент из списка.
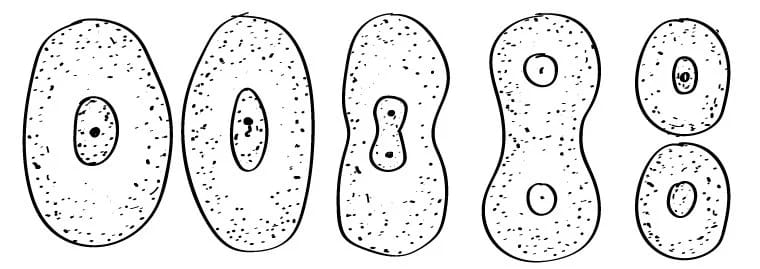
При этом отборе генеральная совокупность делится на группы, которые не пересекаются. Эти группы называются стратами. Элементы в каждой страте однородны по определенным признакам. В каждой страте проводится отбор элементов. Метод отбора может быть любым, при чем не обязательно одинаковым в каждой страте. Отбор из одной страты не зависит от других страт.
Стратегия отбора в этом случае становится более эффективной. Чем больше изменяется исследуемая характеристика, тем большей будет выборка для более точной оценки. А если разбить совокупность на страты, в которых характеристики мало отличаются, то небольшой выборки из каждой страты будет достаточно для оценки всей совокупности.
Пример: исследование уровня доходов по миру. Вначале весь мир делится на страты, а именно страны. Это области, которые не пересекаются между собой, затем исследование проводится по каждой стране отдельно.
В этом случае сложно оценить вероятность попадания каждого элемента совокупности в сэмпл. Исследователи, использующие эти методы, не могут сделать точные выводы о генеральной совокупности.
Если непосредственный отбор из совокупности невозможен, элементы генеральной совокупности объединяются в кластеры.
Кластерный отбор может проходить в одну стадию, тогда сначала отбирают кластеры, а потом исследуют все элементы отобранных кластеров. Например, при исследовании города, кластером может быть семья или жители одного дома.
Если отбор осуществляется в две стадии, то совокупность делят на кластеры, которые состоят из других, более мелких кластеров. На первой стадии получают вероятностную выборку первичных кластеров. На второй стадии — из первичных кластеров отбирают элементы.
Процедура может состоять из трех и более стадий, тогда такая схема называется многостадийной.
Элементы отбираются исходя из того, находятся ли они в простом доступе. Такие выборки очень легко составлять, но нет ни единой гарантии что она будет репрезентативной.
Обычно используется при отборе кандидатов в специфической небольшой группе экспертов. Выбирается один человек для опроса, затем он должен посоветовать несколько других людей и так далее.
В идеале лучше работать со всей генеральной совокупностью, но это занимает много времени и ресурсов. Поэтому можно исследовать только ее часть, что и называется выборкой. Затем исследуются элементы, которые попали в выборку. На основе полученных значений оцениваются неизвестные элементы выборки.

Основные принципы отбора в выборку
Идея состоит в том, чтобы перенести результаты на всю генеральную совокупность. Поэтому выборка должна быть репрезентативной. Другими словами она пропорциональна как подгруппам, так и всей совокупности, и не исключает каких-либо отдельных групп.
Выборка должна быть настолько большой, насколько это возможно, чтобы избежать ошибочных суждений. По сути выборкой может быть любое подмножество генеральной совокупности.
Если выборка недостаточно репрезентативна — исследование будет считаться предвзятым. Если она будет недостаточно большой — неточным.

Если правильно подобрать связь между выборкой и совокупностью, тогда можно сделать правильные заключения о природе всей совокупности. Лучше быть возможно правым, чем точно не правым.
Схемы отбора для вероятностных выборок
Вероятностные выборки подразумевают, что исследователь абсолютно уверен в связях выборки с генеральной совокупностью. Если же связи не прослеживаются или в наличии имеются не все элементы генеральной совокупности используется невероятностная выборка.
На основе жеребьевки
Схема отбора состоит в том, чтобы провести ряд испытаний без возвращения элемента в генеральную совокупность. Каждый элемент совокупности имеет одинаковые шансы попасть в выборку.
Из генеральной совокупности N случайным образом отбирается один элемент, вероятность попадания элемента в выборку равна 1/N. Затем из выборки N-1 выбирается второй элемент с вероятностью 1/(N-1) и так далее до n-го элемента с вероятностью 1/(N-n).
Отбор Бернулли
Отбор происходит из упорядоченного списка из N элементов. Пусть наперед задано некоторое число ? (1<?<0) и набор N независимых реализаций равномерно распределенной на [0,1] случайной величины ?1…?N. Каждому элементу k ставится в соответствие значение. Если ?к<?, то этот элемент отбирается, в другом случае — нет. Возможность того, что элемент будет выбран равна ? для каждого из N элементов. Таким образом каждый элемент, который попал в выборку является биномиально распределенной величиной.
Систематический отбор
Пусть N — размер генеральной совокупности. а — некоторое фиксированное число. а ? N. Первый элемент выборки выбирается случайным образом среди первых a элементов совокупности. Выбранное число r 1? r ?a называется случайным стартом (началом), а число а — выборочным интервалом. Каждый элемент [1,2… а] имеет одинаковую вероятность быть выбранным, равную 1/а. Далее в выборку попадают элементы с шагом а.
Можно получить а разных выборок, каждая из которых имеет одинаковую вероятность быть выбранной.
Простой случайный отбор с возвращением
Во всех вышеизложенных схемах у элемента не было возможности попасть в выборку более 1 раза.
Это логично, так как при повторном включении элемента новая информация не добавляется. Но в этом случае некоторые оценки имеют очень простые статистические свойства, что дает возможность исследовать довольно сложные процедуры отбора.
Например, выполняется m независимых отборов элементов из генеральной совокупности размера N с одинаковыми вероятностями 1/N. Отобранный элемент возвращается в совокупность. Таким образом все N элементов участвуют в отборе постоянно.
Пропорциональный отбор: с возвращением и без
Предполагает, что все числа генеральной совокупности должны быть хорошо перемешаны. Тогда исследователь берет каждый а-й элемент из списка.

Стратифицированный отбор
При этом отборе генеральная совокупность делится на группы, которые не пересекаются. Эти группы называются стратами. Элементы в каждой страте однородны по определенным признакам. В каждой страте проводится отбор элементов. Метод отбора может быть любым, при чем не обязательно одинаковым в каждой страте. Отбор из одной страты не зависит от других страт.

Стратегия отбора в этом случае становится более эффективной. Чем больше изменяется исследуемая характеристика, тем большей будет выборка для более точной оценки. А если разбить совокупность на страты, в которых характеристики мало отличаются, то небольшой выборки из каждой страты будет достаточно для оценки всей совокупности.
Пример: исследование уровня доходов по миру. Вначале весь мир делится на страты, а именно страны. Это области, которые не пересекаются между собой, затем исследование проводится по каждой стране отдельно.
Схемы отбора для невероятностных выборок
В этом случае сложно оценить вероятность попадания каждого элемента совокупности в сэмпл. Исследователи, использующие эти методы, не могут сделать точные выводы о генеральной совокупности.
Кластерный отбор
Если непосредственный отбор из совокупности невозможен, элементы генеральной совокупности объединяются в кластеры.
Кластерный отбор может проходить в одну стадию, тогда сначала отбирают кластеры, а потом исследуют все элементы отобранных кластеров. Например, при исследовании города, кластером может быть семья или жители одного дома.
Если отбор осуществляется в две стадии, то совокупность делят на кластеры, которые состоят из других, более мелких кластеров. На первой стадии получают вероятностную выборку первичных кластеров. На второй стадии — из первичных кластеров отбирают элементы.
Процедура может состоять из трех и более стадий, тогда такая схема называется многостадийной.
Типовой отбор
Элементы отбираются исходя из того, находятся ли они в простом доступе. Такие выборки очень легко составлять, но нет ни единой гарантии что она будет репрезентативной.
Снежный ком
Обычно используется при отборе кандидатов в специфической небольшой группе экспертов. Выбирается один человек для опроса, затем он должен посоветовать несколько других людей и так далее.
Конспект
- Выборки бывают вероятностные и невероятностные.
- Если неправильно выбран метод отбора в выборку. исследование может стать предвзятым или неточным.
- Лучше быть возможно правым, чем точно не правым.


ffriend
Лучше быть правым с известной вероятностью / доверительным интервалом. Само по себе определение «быть возможно правым» не несёт в себе никакой полезной информации — может мы правы, а может и нет, может через 5 минут в эту дверь войдёт динозавр, а может и нет.
Каждый элемент является просто элементом. Ничего ни про какое распределение он знать в принципе не может, ибо он не является случайной величиной. Распределение Бернулли в этом случае имеет только размер сэмпла.