
Привет, Хабр!
Новогодние праздники — отличное время, чтобы отдохнуть от IT использовать профессиональные навыки в любимом хобби. Ковыряясь на сайте рейтинга спортивного ЧГК, я обнаружил отличный API, позволяющий получить данные о всех играх всех турниров. Так у меня появилась идея построить граф сообщества знатоков и проверить теорию шести рукопожатий на географически разбросанном и строго оффлайновом коммьюнити. Под катом картинки графов и бесполезная статистика.
Для начала краткий ликбез, что такое спортивное ЧГК.

Уверен, что с телевизионной версией «Что? Где? Когда?» с волчком и письмами телезрительниц читатель знаком. Спортивное ЧГК — это расширение телевизионного формата, позволяющее играть нескольким командам одновременно.
В кафе, доме молодёжи, актовом зале университета собираются несколько команд численностью до шести человек. Ведущий зачитывает вопросы, на размышление даётся по одной минуте. По окончании минуты команда записывает ответ на игровой бланк и поднимает вверх. Специально обученные люди, именуемые ласточками, собирают бумажки. Обычно за игру читается 36 вопросов, разделённые в три тура. Кто больше всех ответил, тот и молодец.
Существует много турниров по ЧГК, есть даже чемпионат Европы и мира, любопытных отсылаю к авторитетнейшему источнику информации. А примеры вопросов можно найти тут.
Получение данных
Будем считать, что игроки знакомы друг с другом, если они сыграли хотя бы раз за одним игровым столом. Благодаря хорошему API скачивание данных о всех турнирах и всех командах не представляет проблем.
Под спойлерами не используется даже Beautiful Soup, только requests. Jupyter notebook со всем исходным кодом будет в конце статьи.
url = 'https://rating.chgk.info/api/tournaments.json/?page={}'
df = pd.DataFrame(columns=['name', 'start'])
for i in range(1, 7):
data = requests.get(url.format(i)).json()
for item in data["items"]:
df.loc[item["idtournament"]] = (item["name"], item["date_start"])
df.to_csv('tournaments.csv')Осталось скачать игровые составы всех турниров и запомнить все знакомства. Первоначально я планировал хранить факты совместной игры в DataFrame, однако скорость добавления новых записей оказалось удручающей. Поэтому заведём set из tuple'ов (id1, id2), где id1, id2 — идентификаторы игроков, знакомых между собой. Заодно избавимся от дубликатов.
df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0')
url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json'
links = set()
for id in df.index:
teams = requests.get(url.format(id)).json()
for team in teams:
t = team["recaps"]
for i in range(len(t)):
for j in range(i + 1, len(t)):
first = int(t[i]["idplayer"])
second = int(t[j]["idplayer"])
if first < second:
links.add((first, second))
else:
links.add((second, first))
# побережём сайт рейтинга
sleep(1)
clear_output(wait=True)
display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df)))
display('Links total: ' + str(len(links)))Получение графа и исследование компонент связности
Итак, с подготовкой данных покончено, пора строить граф! Для этого воспользуемся библиотекой networkx, возможностей которой вполне достаточно для нашего кластера.
players = itertools.chain(*links)
G = nx.Graph()
G.add_nodes_from(players)
for t in links:
G.add_edge(*t)
print(nx.info(G))Сейчас в сообществе ЧГК около двухсот тысяч человек, а в среднем знаток за карьеру играл с 12 людьми:
Number of nodes: 198145
Number of edges: 1206076
Average degree: 12.1737Пришло время узнать, сколько компонент связности есть в графе знакомств. В networkx есть замечательная функция connected_components, которая делает как раз то, что нужно:
clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)]
print(clusters_l[:20])Почти три четверти игроков состоят в одной компоненте связности, остальные разбиты по очень маленьким подграфам. Всего их более восьми тысяч.
[145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35]Даже в логарифмическом масштабе доминирование главной компоненты выглядит внушительно. По оси Х — номер компоненты от большей к меньшей, по оси Y — её размер (ось логарифмическая).

Чем же вызвано такое неравномерное распределение людей по связным компонентам? На мой взгляд, дело в следующем:
- небольшая группа людей первый раз приходит на игру и тем самым образует небольшой кластер на 4-6 человек;
- если в городе уже есть большое коммьюнити, такой кластер очень быстро сольётся с главным — достаточно всего одному человеку сыграть за команду из основного кластера;
- если же в городе ЧГК только появилось, кластер проживёт дольше, т.к. сыграть за команду из основного кластера сложнее.
Процесс напоминает образование дождевых капель в облаках: большая капля притягивает маленькие и быстро растёт.
Прежде чем заняться основном компонентой, давайте посмотрим на компоненты на первом-девятом месте (считаю основную компоненту нулевой). Проверим гипотезу, что люди в этих компонентах из одного города. У знатока нет привязки к городу (что логично в нашем современном мире). Однако можно посмотреть на порт приписки команды, за которую он играл в последний раз
for i in range(1, 10):
_g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i])
s = pd.Series()
p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json'
t_url = 'https://rating.chgk.info/api/teams/{}.json'
for player in _g:
data = requests.get(p_url.format(player)).json()
for item in data:
team_id = data[item]["tournaments"][0]["idteam"]
data = requests.get(t_url.format(team_id)).json()
town = data[0]["town"]
s.at[len(s)] = town
print('Кластер #{}'.format(i))
print(s.value_counts())Итоговая табличка:
| № компоненты связности | Размер | Города |
|---|---|---|
| 1 | 153 | Керчь |
| 2 | 124 | 110 — Усть-Илимск, 12 — Владивосток, 2 — Иркутск |
| 3 | 74 | Тамбов — 72, Люксембург — 2 |
| 4 | 72 | Лесной |
| 5 | 56 | Ейск |
| 6 | 50 | Бишкек |
| 7 | 47 | Горно-Алтайск |
| 8 | 42 | Житомир — 37, Глазов — 5 |
| 9 | 40 | Горно-Алтайск — 31, Москва — 9 |
Да, малые кластеры почти полностью из одного города. Прошу обратить внимание на компоненту из семидесяти двух тамбовчан, которая связана с Люксембургом. На седьмом и девятом месте компоненты из Горно-Алтайска, которые почему-то не связаны между собой. Мне охотно представляется борьба двух ЧГК-ашных кланов, наподобие Монтекки и Капулетти, которые бьются за контроль над городом.
Предположу, что в ближайшем будущем эти компоненты вольются в состав основной, но будут продолжать бороться.
Основная компонента связности
Итак, мы подобрались к основной компоненте. Получим нужный подграф и посмотрим на его статистику:
subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0])
subgraph = G.subgraph(subgraph_v)
print(nx.info(subgraph))Среднее число связей получилось больше.
Number of nodes: 145922
Number of edges: 1070504
Average degree: 14.6723А каково максимальное количество связей одного игрока?
for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]:
print('Игрок {} играл с {} игроками'.format(t[0], t[1]))Игрок 42511 играл с 818 игроками
Игрок 15051 играл с 798 игроками
Игрок 29800 играл с 678 игроками
Игрок 23020 играл с 666 игроками
Игрок 16581 играл с 662 игроками
Игрок 5328 играл с 657 игроками
Игрок 29887 играл с 651 игроками
Игрок 15811 играл с 645 игроками
Игрок 30352 играл с 605 игроками
Игрок 1055 играл с 602 игрокамиПризнаться, я немного шокирован полученными цифрами. Если каждый раз играть с новой командой, то понадобится 818/5 ? 164 игры, чтобы выйти на первое место. Невероятно.
Первых двух знатоков в этом рейтинге мы запомним и будем использовать их коммуникативные навыки далее.
Давайте оценим, сколько ближайших знакомств у среднего знатока:
_count = 50
values = nx.degree_histogram(subgraph)
plt.figure(figsize=(16, 8), dpi=80)
plt.plot(range(_count),values[:_count],'ro-') # in-degree
plt.xlabel('Число знакомств', fontsize=18)
plt.xticks(range(0,_count, 5))
plt.ylabel('Число игроков', fontsize=18)
plt.title('Число знакомств', fontsize=22)
plt.show()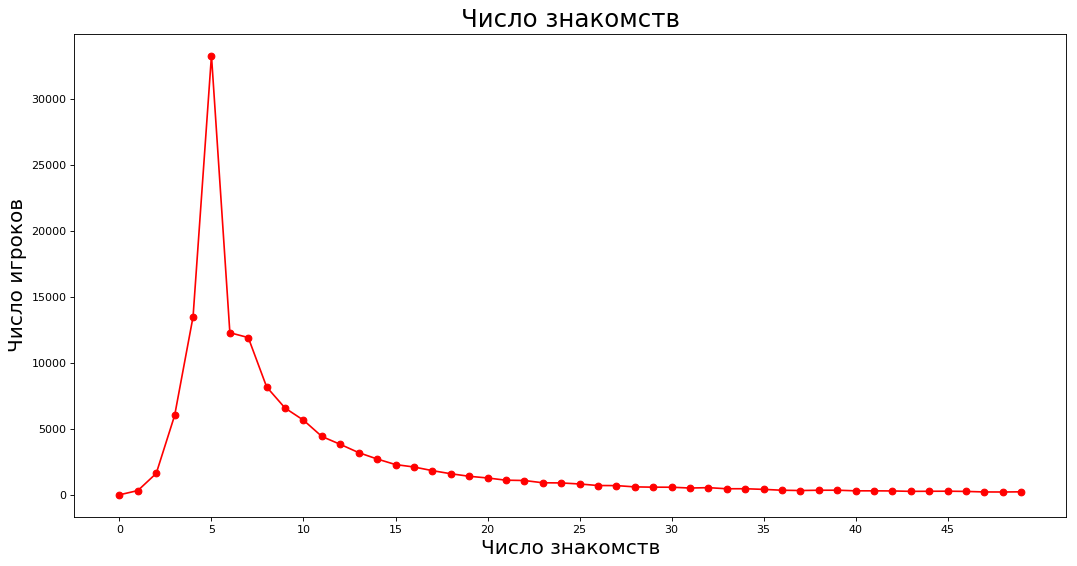
По оси X — число ближайших знакомств, по оси Y — количество знатоков, которое имеет соответствующее число знакомств. Например, по пять знакомств имеют приблизительно 40 000 знатоков.
Отметим, что мода — 5 знакомств (забавно, что за столом может находиться до шести человек). При этом среднее арифметическое числа знакомств — 14.67, а медиана — 7. Дело в том, что господа из рейтинга выше сильно завышают среднее. Если сто человек не играют в ЧГК, а один имеет 800 знакомств, то в среднем они играют в ЧГК.
Расстояния до игроков
Т.к. считать диаметр такого графа немного сложно, поступим проще: возьмём список из нескольких игроков и найдём максимальное из кратчайших расстояний от них до других знатоков. В качестве этих игроков я взял нескольких известных знатоков, себя, случайного игрока и двух знатоков с наибольшим числом знакомств (см. рейтинг выше). Вот что получилось:
famous_players = {9808: 'Александр Друзь',
5195: 'Анатолий Вассерман',
25882: 'Максим Поташев',
29333: 'Михаил Скипский',
118622: 'Михаил Атепаев',
42511: 'Николай Некрылов',
15051: 'Георгий Коколия',
118621: 'Михаил Акулов'}
for key in famous_players:
print('{}: {} - максимальное расстояние от игрока до других'
.format(famous_players[key],
nx.eccentricity(subgraph, v=key)))
Александр Друзь: 12 - максимальное расстояние от игрока до других
Анатолий Вассерман: 12 - максимальное расстояние от игрока до других
Максим Поташев: 12 - максимальное расстояние от игрока до других
Михаил Скипский: 12 - максимальное расстояние от игрока до других
Михаил Атепаев: 13 - максимальное расстояние от игрока до других
Николай Некрылов: 12 - максимальное расстояние от игрока до других
Георгий Коколия: 13 - максимальное расстояние от игрока до других
Михаил Акулов: 13 - максимальное расстояние от игрока до других
Получается, что сильная формулировка теории шести рукопожатий (любые два человека разделены не более чем пятью уровнями общих знакомых) неверна. Диаметр графа, скорее всего, равен 13-14.
А что насчёт более слабой формулировки (любые два человека в среднем разделены не более чем пятью уровнями общих знакомых)?
for key in famous_players:
paths = nx.shortest_path_length(subgraph, source=key).values()
print('{}: {} - среднее расстояние от игрока до других'
.format(famous_players[key],
sum(paths) / len(paths)))
Александр Друзь: 3.941461876893135 - среднее расстояние от игрока до других
Анатолий Вассерман: 3.7971107852140182 - среднее расстояние от игрока до других
Максим Поташев: 3.89353216101753 - среднее расстояние от игрока до других
Михаил Скипский: 3.8634887131481204 - среднее расстояние от игрока до других
Михаил Атепаев: 4.1443373857266215 - среднее расстояние от игрока до других
Николай Некрылов: 3.575478680390894 - среднее расстояние от игрока до других
Георгий Коколия: 3.608674497334192 - среднее расстояние от игрока до других
Михаил Акулов: 4.564102739819904 - среднее расстояние от игрока до других
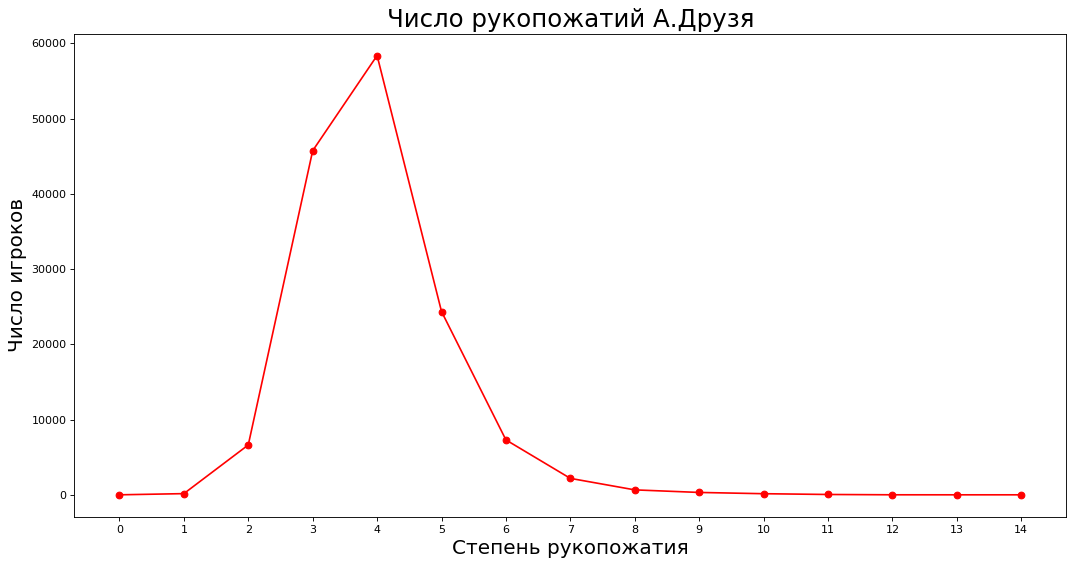
Если ослабить формулировку, то теория выполняется — в среднем между знатоками 4-5 уровней знакомств. Построим график, сколько людей знакомы со случайным знатоком А.Друзём напрямую, через одного, двух и т.д. знатоков.
paths = nx.shortest_path_length(subgraph, source=9808)
neighbours = [0] * 15
for k in paths:
neighbours[paths[k]] += 1
_count = 15
plt.figure(figsize=(16, 8), dpi=80)
plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree
plt.xlabel('Степень рукопожатия', fontsize=18)
plt.xticks(range(_count))
plt.ylabel('Число игроков', fontsize=18)
plt.title('Число рукопожатий А.Друзя', fontsize=22)
plt.show()По оси X степень знакомства с А.Друзём (напрямую, через одного, двух и т.д.), по оси Y — количество знатоков, которые знакомы с А.Друзём таким образом.
Социальные графы
Т.к. строить граф на почти 200 тысяч человек не очень хорошая идея, сделаем проще: построим Керченскую компоненту связности и граф людей, связанных с автором.
Керченская компонента
little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1])
little = G.subgraph(little_v)
plt.figure(figsize=(24, 12), dpi=200)
pos = nx.kamada_kawai_layout(little)
nx.draw(little, pos=pos, node_size=100, edge_color='gray',
node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet)
plt.show()
Видно разделение компоненты на команды. При этом команды связаны между собой с помощью, как правило, одного-двух общительных знатоков. В центре довольно небольшое ядро знатоков, игравших с большим количеством других игроков.
Граф одного человека
Найдём ближайших знакомых одного человека и посмотрим, насколько они связаны между собой. Для упрощения графа не будем добавлять самого человека (он и так со всеми связан)
id = 118622
ego_graph = [n for n in G.neighbors(id)]
#ego_graph.append(id)
ego_graph = G.subgraph(ego_graph)
plt.figure(figsize=(24, 16), dpi=200)
pos = nx.kamada_kawai_layout(ego_graph)
nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray',
node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet)
plt.show()
Граф существенно плотнее, различимо ядро из 10-15 человек, которые хорошо знакомы друг с другом. Размер максимальной клики равен 13.
Заключение
- В спортивном ЧГК познакомиться с человеком значительно труднее, чем в социальной сети, необходимо выйти в оффлайн и сыграть хотя бы один турнир. При этом знатоки разбросаны по всему земному шару. Тем не менее, среднее расстояние между знатоками действительно меньше пяти.
- На сайте рейтинга используется число Снятковского, которое является аналогом числа Эрдёша в мире ЧГК. Сам господин Снятковский занимает третье место в нашем рейтинге самых коммуникабельных знатоков.
- Код из статьи в моём гитхабе.
- За ценные замечания автор выражает благодарность командам "Белый шум" и "Кто подставил Роджера Федерера", Михаилу Акулову, Вере Терентьевой и Firemoon.
Комментарии (22)

trawl
11.01.2020 23:24Читая статью, глаз заселился за город Горно-Алтайск. Я там не живу с 2011 года, но решил зайти на сайт и посмотреть, кто там есть из знакомых. 18 знакомых человек насчитал (из 419), ещё несколько заочно знакомых. При этом я далёк от ЧГК...
Кстати, даже не в курсе был, что в ГА проводят спортивное ЧГК, но в соцсетях замечал, что знакомые из списка любят во всякие квизы. Или квиз это и оно и есть?

atepaevm Автор
12.01.2020 00:02Нет, это не квизы. Более того, чгкашники обычно обижаются на это сравнение :)
В Горно-Алтайске есть площадка для проведения именно ЧГК.


Surround
С чего бы? Для теории рукопожатий мы берём любых знакомых, а не ограничиваемся только теми, которые играют в ЧГК. Если округлить население планеты до 8 миллиардов, то получим loga(8.0E+9) = 6, т.е. основание a?44.7
Если выбросить всех младенцев, затворников и прочих социопатов, то выходит в среднем на каждого человека надо по 45 уникальных знакомых, чтобы Теория оказалась верна. Вполне похоже на правду.
Eldhenn
Если знакомыми считать всех, с кем познакомился в школе-институте-армии, можно и до сотни дойти.
fougasse
Так, скорее, до тысячи.
Сотня — это реально очень мало, если про знакомых в самом слабом смысле.
Школа, (высшее образование), соседи, коллеги, сфера услуг — уже набежит сотня-другая.
Конечно, если "мамкин хиккан" — всё иначе.
Surround
Если мы берём понятие «знакомый» в широком смысле, т.е. тот с кем мы представлены друг другу и при встрече приветствуем его, то соглашусь, 1000 — оценка нужного порядка.
Но нам особенно важна уникальность, чтобы ни на каком из 6 уровней эти самые знакомые больше не повторились. Иначе наше дерево начинает содержать циклы и заветные 8 миллиардов листовых узлов уже не получить.
atepaevm Автор
Приведённая цитата относилась именно к ЧГК.
Но и если говорить про реальный мир, я сомневаюсь, что шести рукопожатий хватит. Я даже сомневаюсь, что весь мир связан, привет аборигенам Австралии и Амазонии. Однако спорить тут бесполезно, т.к. проверить теорию нельзя.
RigelNM
Пару лет назад здесь была статья по данным из Facebook и там таки было меньше 5ти.
Surround
В таком случае моя вина, не верно понял.
Читал статью на тему исследования социальных связей (очень бы сейчас пригодилась ссылка, но увы не сохранил). Там вводились понятия superconnector и gate. Суперконнекторы — люди, у которых количество устойчивых социальных связей больше на 1+ порядок, чем в среднем по больнице. Вот эти люди очень помогают прыгать с континента на континент по короткому маршруту. А гейт — пара людей образующих единственную связь на входе в некоторую изолированную группу. Якобы для большинства изолированных групп такие гейты существуют.
Если взять какое-нибудь племя аборигенов, то раз нам известен сам факт его существования где-то в глубинах Амазонки, значит эта информация каким-то путём до нас дошла и скорее всего это был гейт «вождь племени — вождь соседнего — <...>» или «вождь — участник обнаружившей экспедиции — <...>». То есть полной изоляции всё равно не получается.
GreyStrannik
Давайте попробуем набросать возможную схему связей:
- Рядовой абориген Австралии
- Вождь племени
- Рядовой бюрократ по делам племён
…- 1-2 человека-суперконнектора типа работника ресепшена гостиницы, паспортиста на таможне или кассира сиднейского метро
…Получается более 6-ти рукопожатий.
Surround
Вы сейчас взяли произвольный маршрут в графе и пытаетесь опровергнуть теорию о рукопожатиях, утверждая что этот маршрут является кратчайшим. Но такое можно утверждать только если нам на 100% известны все вершины в этом графе.
С таким же успехом в вашем примере жена бюрократа по делам племён могла однажды посетить Москву в ходе туристической поездки, и там в парке Горького познакомиться с некоторым гражданином России, который имеет родственников на Алтае, и уже очередным родственником одного из этих родственников является наш искомый житель обычного алтайского хутора. Итого 6 рукопожатий.
Для меня самым убедительным в этой теории было проследить собственную связь до произвольного главы иностранного государства. На четвёртом рукопожатии нашёлся выход на собственного президента, на пятом получаем связь с арабским шейхом. Хотя казалось бы где я и где арабский шейх.
GreyStrannik
Вы правы и можете попробовать реализовать своё утверждение. Ведь теории необходимо доказывать, а недоказуемные теории ненаучны.
При этом прошу отметить, что я рассматривал слабый случай связности — между людьми должна быть хотя бы либо сделка, либо общение, а в теории связность предполагается более сильная — знакомство, то есть люди идентифицирую свою связь как знакомство (например, я не идентифицирую свою связь с продавщицами окрестных магазинов как знакомство, а в предложенном примере такое учитывается).
Surround
Согласен, пока теория не будет содержать исчерпывающего описания какую связь следует считать устойчивой, кого в рамках теории можно считать знакомым, а кого нет, то она так и останется недоказанной.
GreyStrannik
А разве данная теория не содержит такого исчерпывающего описания?
Surround
Я дальше статей английской вики так и не ушёл, времени жалко. Может в каких-то научных статьях за авторством самого Милгрэма такое описание и есть. Но совершенно точно его нет ни в оригинальной вики-статье, ни в статье «Small-world experiment», в которой описано как они письма по США пересылали.
Нигде не сказано «You should understand the acquaintanceship term as ...», только вскользь упоминается, что «weak and strong acquaintance links are needed». Из эксперимента с письмами можно подумать, что если вам известен чей-то почтовый адрес, т.е. вы можете в любой момент связаться с человеком, то ваша связь уже в достаточной степени стронг. В переводе на современные реалии это бы означало, что для констатации знакомства достаточно наличия контакта в мессенджере или даже просто знать ник на каком-нибудь форуме. Но по сути это слишком широкая трактовка, которая мало чем будет отличаться от той же связи через продавщицу окрестного магазина.
trawl
Но житель Алтая мог быть тем самым, кто летал в Австралию.
Например, у меня двоюродная сестра живёт на Алтае. Она работала на круизном лайнере и может оказаться супер-коннектором. Т.е. есть ряд обычных жителей Алтая (знакомые моей сестры), которые за 6 рукопожатий выходят на вождя.
А вот хуторов на Алтае нет.
atepaevm Автор
Жаль, что нет ссылки на статью, с удовольствием бы почитал.
Примечательно, что даже в на небольших графах из статьи видны и гейты, и суперконнекторы.
Мне кажется, что ещё есть неизвестные нам племени или деревеньки. Но это уже получаются рассуждения скорее о чайнике Рассела, которые нельзя ни подтвердить, ни опровергнуть.
Sunny-s
Опровергнуть — нельзя, но если спросить Илона Маска, не клал ли он чайник в бардачок своего Родстера, и он ответит, что клал — можно подтвердить :)
Vsevo10d
Тут речь о некоторых спорных утверждениях. Какой уровень знакомства требуется? Человек видел этого человека много раз, но не знает имени (продавщица-суперконнектор)? Человек видел человека 1 раз и жал ему руку (деловой визит)? Человек у человека в соцсети (телефонной книжке, ежедневнике, переписке в почте)?
Причем связи могут работать еще вниз или вверх. Например, через одного человека я рукопожат с Путиным (и вряд ли они пожмут руки больше одного раза в жизни), и значит, три рукопожатия до всех Матвиенок, Зюгановых, губернаторов, президентов Большой Восьмерки, США,
членов Богемской Рощи, масонов, рептилоидов,— но не простой народ (вон, выяснилось, что продавщица мороженого на МАКСе тоже специальная). А вот через участкового я знаком со всеми экс-сидельцами и бичуганами района (и вряд ли у них принято жать руку мусорам, хотя по закону общаются они не реже раза в неделю). А вверх там всякие начальники УВД, полковники, генералы — до того же президента хорошо если дотягивает за шесть.Что до соцсетей, то когда я был еще активным пользователем ВК был такой прикол (сейчас его вроде убрали), что друзья человека в списке ранжированы по близости к тебе. И я брал знакомого, у него в друзьях выбирал первого-второго сверху друга, у того — тоже первого второго сверху, и натыкался на человека, у которого были со мной два-три общих друга в такой конфигурации (типа он знает моего одноклассника, одногруппника и еще какого-нибудь рандомного чела, незнакомых друг с другом), что я офигевал, насколько тесен мир. Или наоборот, вводил что-то типа «Сергей Петров» из Владивостока и через 3-4 «верхних друга в списке» выходил на себя. Повторюсь, сейчас эта фишка не особо работает, да и приватные аккаунты наконец-то завезли.
GreyStrannik
Теория гласит, что 6 рукопожатий это не в среднем, а максимум. При этом она базировалась на эксперименте с конвертами. У эксперимента был целый ряд недостатков. Например, не учитывались конверты, не дошедшие до адресатов, а значит была Систематическая ошибка выжившего. Например, конверты посылались от жителя США жителю США, а жители США образуют весьма связный граф.
Другие эксперименты, к сожалению, тоже не охватывают крайних случаев, например, связности людей-изолятов на разных материках. И таких крайних случаев не мизер, которым можно было бы пренебречь.
atepaevm Автор
Уверен, что есть несколько вариантов формулировки, в статье я практически процитировал вариант из русской Википедии. Там имеется в виду именно диаметр графа.
Да, к сожалению, доказать или опровергнуть теорию явно невозможно из-за невозможности сформулировать знакомства каждого человека на Земле.