
Не-не-не, если сейчас я это сделаю, то вы и читать-то статью не будете. Это будет. но позже. А прежде я хочу описать задачу, с которой все началось:
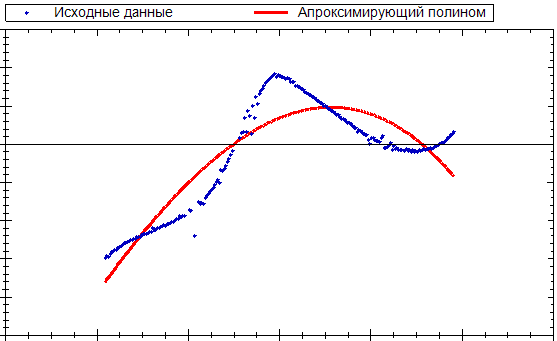

Прям перед вами достаточно качественная аппроксимация по мнению алгоритма. Его винить-то не в чем: сходимость к результирующему полиному крайне медленная, средне квадратичное отклонение меняется нехотя, а из-за малого количества исходных точек (всего около двух сотен) распределение невязок в первом приближении выглядит как нормальное.
И вот, в поисках универсального критерия. который позволил бы мне отличить случайную последовательности от регулярной (я в курсе, что это целая проблема, но все же), пришла идея использовать фракталы. Дело в том, что размерность случайного блуждания =1.5. Есть надежда, что вычислив размерность кривой невязок, мы получим 1.5 +- разумные величины.
Вычислять размерность Хаусдорфа — это еще та затея, а вот с Минковским все гораздо проще, хотя и с ним пришлось попотеть.
Применим подход, который используется в отправной статье: меняя масштаб будем считать количество прямоугольников N, через которые проходит кривая. Получив зависимость log(N(e))/log(e) аппроксимируем прямойс помощью МНК. Искомая нами метрика — коэффициент наклона.
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList)
{
double minY = Double.MaxValue, maxY = Double.MinValue;
double minX = minY, maxX = maxY;
foreach (var pair in dataList)
{
if (minY > pair.Value)
minY = pair.Value;
if (maxY < pair.Value)
maxY = pair.Value;
if (minX > pair.Key)
minX = pair.Key;
if (maxX < pair.Key)
maxX = pair.Key;
}
m_bottomLeftY = minY;
m_bottomLeftX = minX;
return calculate(dataList, maxX, maxY);
}
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY)
{
if( dataList.Count() < 2) return 0;
for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){
double XScale = (maxX - m_bottomLeftX) / scaleNumber;
double YScale = (maxY - m_bottomLeftY) / scaleNumber;
var enumerator = dataList.GetEnumerator();
fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale);
int count = calculatedNumberBoxesAndReset(scaleNumber);
if (count == 0) count = 1;
m_boxesNumber[scaleNumber - StartSize] = Math.Log(count);
}
m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber);
return m_linearApproximator.resultPolinomal.a[1];
}
double m_bottomLeftX, m_bottomLeftY;
В отличии от исходной статьи я меняю масштаб не в геометрической прогрессии, а в арифметической, слишком мало данных для первой. m_linearApproximator — это обертка над МНК, ничего умного и сложного, а сам МНК можно найти либо в исходной статье. либо в MathNet.Numerics. Строчка if (count == 0) count = 1 возникла из-за особенностей реализации. Она покрывает тот случай, когда у нас всего одна точка.
Вся магия находится в методе fillBoxes, именно здесь заполняются квадраты:
void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY)
{
double prevX=0, prevY=0, targetX=0, targetY=0;
dataIterator(ref prevX, ref prevY);
int indexY = FinishSize, indexX = FinishSize;
int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ;
m_Boxes[currentIndexY, currentIndexX] = true;
double[] CrossPosition = new double[2];
while (dataIterator(ref targetX, ref targetY))
{
if(prevX == targetX && prevY == targetY)
continue;
bool isBottom = targetY - prevY < 0;
bool isLeft = targetX - prevX < 0;
double a = (targetY - prevY) / (targetX - prevX), fracA=1/a;
double b = targetY - a * targetX;
double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY;
CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b;
CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA;
while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) ||
(targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )//Нужно ли делать следующий шаг?
{
if ( (bottomBorder - CrossPosition[0])/stepY <= 1E-9 && (CrossPosition[0] - bottomBorder - stepY)/stepY <= 1E-9)
currentIndexX += isLeft ? -1 : 1;
if ( (leftBorder-CrossPosition[1])/stepX <= 1E-9 && (CrossPosition[1] -leftBorder - stepX)/stepX <= 1E-9 )
currentIndexY += isBottom ? -1 : 1;
m_Boxes[currentIndexY, currentIndexX] = true;
leftBorder = m_bottomLeftX + currentIndexX * stepX;
bottomBorder = m_bottomLeftY + currentIndexY * stepY;
CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b;
CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA;
}
prevY = targetY;
prevX = targetX;
}
}
Исходные данные для меня — это набор точек. Про ни единственное что известно -, что измеряемый процесс непрерывен, а вот в сам процесс совсем произвольный: к случайным помехам разной мощности могу возникать и исчезать аддитиваня помеха. В этом случае единственный выход — линейная интерполяция. Как следствие малости входных данных ошибки связанные при проходе прямой через узел решетки недопустимы.
С учетом этих условий универсальное решение, допускающее расширение на любую размерность — пошаговый переход от квадрата к квадрату. (Сразу предупреждаю, в продемонстрированном коде не учтены случаи, когда прямая вертикальна или горизонтальна)
public class MinkowskiDimension
{
public MinkowskiDimension(int startSize, int finishSzie)
{
StartSize = startSize; FinishSize = finishSzie;
}
public MinkowskiDimension()
{
}
public int StartSize
{
get { return m_startSize; }
set
{
m_startSize = value;
if (m_startSize < m_finishSize)
{
m_scaleArgument = new double[m_finishSize - m_startSize];
for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = - Math.Log(m_startSize + i);
m_boxesNumber = new double[m_scaleArgument.Count()];
}
}
}
int m_startSize;
public int FinishSize
{
get { return m_finishSize; }
set
{
m_finishSize = value;
m_Boxes = new bool[value, value];
if (m_startSize < m_finishSize)
{
m_scaleArgument = new double[m_finishSize - m_startSize];
for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = Math.Log(m_startSize + i);
m_boxesNumber = new double[m_scaleArgument.Count()];
}
}
}
int m_finishSize;
double[] m_scaleArgument;
double[] m_boxesNumber;
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList)
{
double minY = Double.MaxValue, maxY = Double.MinValue;
double minX = minY, maxX = maxY;
foreach (var pair in dataList)
{
if (minY > pair.Value)
minY = pair.Value;
if (maxY < pair.Value)
maxY = pair.Value;
if (minX > pair.Key)
minX = pair.Key;
if (maxX < pair.Key)
maxX = pair.Key;
}
m_bottomLeftY = minY;
m_bottomLeftX = minX;
return calculate(dataList, maxX, maxY);
}
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY)
{
if( dataList.Count() < 2) return 0;
for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){
double XScale = (maxX - m_bottomLeftX) / scaleNumber;
double YScale = (maxY - m_bottomLeftY) / scaleNumber;
var enumerator = dataList.GetEnumerator();
fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale);
int count = calculatedNumberBoxesAndIbit(scaleNumber);
if (count == 0) count = 1;
m_boxesNumber[scaleNumber - StartSize] = Math.Log(count);
}
m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber);
return m_linearApproximator.resultPolinomal.a[1];
}
double m_bottomLeftX, m_bottomLeftY;
void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY)
{
double prevX=0, prevY=0, targetX=0, targetY=0;
dataIterator(ref prevX, ref prevY);
int indexY = FinishSize, indexX = FinishSize;
int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ;
m_Boxes[currentIndexY, currentIndexX] = true;
double[] CrossPosition = new double[2];
while (dataIterator(ref targetX, ref targetY))
{
if(prevX == targetX && prevY == targetY)
continue;
bool isBottom = targetY - prevY < 0;
bool isLeft = targetX - prevX < 0;
double a = (targetY - prevY) / (targetX - prevX), fracA=1/a;
double b = targetY - a * targetX;
double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY;
CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b;
CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA;
while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) ||
(targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )//Нужно ли делать следующий шаг?
{
if ( (bottomBorder - CrossPosition[0])/stepY <= 1E-9 && (CrossPosition[0] - bottomBorder - stepY)/stepY <= 1E-9)
currentIndexX += isLeft ? -1 : 1;
if ( (leftBorder-CrossPosition[1])/stepX <= 1E-9 && (CrossPosition[1] -leftBorder - stepX)/stepX <= 1E-9 )
currentIndexY += isBottom ? -1 : 1;
m_Boxes[currentIndexY, currentIndexX] = true;
leftBorder = m_bottomLeftX + currentIndexX * stepX;
bottomBorder = m_bottomLeftY + currentIndexY * stepY;
CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b;
CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA;
}
prevY = targetY;
prevX = targetX;
}
}
int calculateIndex(double startvalue, double scale, double value)
{
double index = (value - startvalue) / scale;
int intIndex = (int) index;
return Math.Abs(index - intIndex) > 1E-9 || intIndex ==0 ? intIndex: intIndex -1;
}
int calculatedNumberBoxesAndIbit(int currentScaleSize)
{
int result=0;
for (int i = 0; i != currentScaleSize; ++i)
{
for (int j = 0; j != currentScaleSize; ++j)
{
if (m_Boxes[i, j]){
++result;
m_Boxes[i, j] = false;
}
}
}
return result;
}
bool[,] m_Boxes;
PolinomApproximation m_linearApproximator = new PolinomApproximation(1);
}
Давайте протестируем его на все возможных прямых:
[TestMethod]
public void lineDimensionTest()
{
var m_calculator = new MinkowskiDimension(3, 10);
var data = new List <KeyValuePair<double, double>>();
data.Add(new KeyValuePair<double, double>(0, 1));
data.Add(new KeyValuePair<double, double>(1, 5));
double result = m_calculator.calculate(data);
if (Math.Abs(result - 1) > 1E-9) Assert.Fail();
data.Add(new KeyValuePair<double, double>(2, 9));
result = m_calculator.calculate(data);
if (Math.Abs(result - 1) > 1E-9) Assert.Fail();
data.Clear();
data.Add(new KeyValuePair<double, double>(0, -1));
data.Add(new KeyValuePair<double, double>(1, -5));
data.Add(new KeyValuePair<double, double>(2, -9));
result = m_calculator.calculate(data);
if (Math.Abs(result - 1) > 1E-9) Assert.Fail();
data.Clear();
data.Add(new KeyValuePair<double, double>(0, -1));
data.Add(new KeyValuePair<double, double>(0.5, -3));
data.Add(new KeyValuePair<double, double>(2, -9));
result = m_calculator.calculate(data);
if (Math.Abs(result - 1) > 1E-9) Assert.Fail();
}
Работает и это хорошо. Давайте теперь возьмем квадрат. Аргх, напоролись на то, о чем я предупреждал. Но не беда, давайте квадрат перевернем, а там потом добавим вырожденные случаи:
[TestMethod]
public void squareDimensiontest()
{
var m_calculator = new MinkowskiDimension(3, 15);
var data = new List<KeyValuePair<double, double>>();
data.Add(new KeyValuePair<double, double>(0, 1));
data.Add(new KeyValuePair<double, double>(1, 0));
data.Add(new KeyValuePair<double, double>(0, -1));
data.Add(new KeyValuePair<double, double>(-1, 0));
data.Add(new KeyValuePair<double, double>(0, 1));
double result = m_calculator.calculate(data);
if (Math.Abs(result - 2) > 1E-9) Assert.Fail();
}
Результат 1.1. Брр, что за странность. А нет, понятно, 2 — это для плоской фигуры, для прямоугольника, а не для его контура. Ну ладно, это понятно. Давайте добавим количество масштабов; 1.05; добавим еще; стремимся к единице.
Оказывается, что для конечного объединения множеств размерность Минковского — максимум для размерности каждого из множеств. Т.е. для совокупности прямых размерность 1. Иными словами, наш результат совершенно верен.
Ну вот теперь можно доказать, что Попес не отличается от квадрата. Т.к. контур мы представляем прямыми, то у нас площадь разбивается либо на треугольник, либо квадрат. про квадрат мы все знаем. Какая размерность Минковского у квадрата мы знаем — 2. А у треугольника?
Как не странно, но тоже два. Это, кстати, разбивает предположение в исходной статье, что фрактальная размерность отражает негладкость кривой. Но это кстати, главное что в итоге оцифрованная попа Попес имеет размерность максимальную из 2 и 2.
Еще один интересный пример. Какова размерность у круга?
Тоже два. А у окружности?
Итого: круг, квадрат и треугольник (и попа Лопес) у нас неотличимы, это вносит серьезные трудности в модельной интерпретации для фрактальной размерности. Классическая интерполяция между данными по прямой приводит, что размерности контура стремится к 1, а площадь к двойке. Отсюда очевидно, что без априорных каких-то знаний его вычисление теряет смысл. Ну и также наш маленький тест показал, что ориентация сложной кривой вносит сильное возмущения в наши вычисления, а их оценка крайне затруднена без понимания того, что показывает сам параметр.
Комментарии (11)

mephistopheies
11.08.2015 13:43пришлось даже свой пост перечитать, а то забыл уже о чем там -)
Т.к. контур мы представляем прямыми, то у нас площадь разбивается либо на треугольник, либо квадрат.
мне кажется ваша ошибка в рассуждениях где то вот тут; естественно для дискретного объекта, коем является людое изображение, минимальным разбиением будет вообще один единственный пиксель, тогда размерность такого объекта будет максимальной размерностью из множеств разбиения, верно?
вообще говоря верно, но совсем бесполезно
на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный (а не просто объединение пикселей, или как вы предположили — отрезков), и предположить что мы можем box-count'ингом аппроксимировать только до определенного момента, а далее уже экстраполировать разбиения, в этом и суть алгоритма
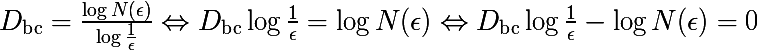
далее обычный подход из машинного обучения:
1 — собрать датасет (как раз аппроксимирование боксами и подсчет их)
2 — обобщить (решить задачу линейной регрессии)
Как не странно, но тоже два. Это, кстати, разбивает предположение в исходной статье, что фрактальная размерность отражает негладкость кривой.
таких предположений там нет, мой пост не о предположения и не гипотезах моих личных, я не ученый, я практик, мой пост о фактах, фактах которые доказаны и приняты
у меня там есть цитата которая имхо отражает, что такое фрактальная размерность
дробная размерность — это своего рода плотность самоподобия
литература
DancingOnWater
11.08.2015 14:12-1Начну с конца:
У вас там есть такая фраза:
«Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.»
Вот за нее я зацепился.
>>на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный
Вот моя последняя часть как раз об этом. На примере теоретического значений для круга квадрата и треугольника, а также того наблюдения, как банальный поворот банального квадрата вносит ошибку и как это ошибка убывает я длеаю заключение, что натравливать алгоритм на распознавание изображений или другого ряда данные, не будучи уверенным, что это фрактал, практически бесполезно.
mephistopheies
11.08.2015 14:18а что в реальном мире фрактал?

DancingOnWater
11.08.2015 15:07Очень много что. Облака, горы, деревья, лес, человеческий мозг, раковые образования и т.д… Например, статья, ссылку на которую вы даете ниже — это исследование компьютерных методов в маммографии. И тут я не удивлен.

mephistopheies
12.08.2015 12:26отлично, но изображение любого из этих объектов будет очевидно не фрактальным, в том то и суть, не имея возможность исследовать фрактальность реальных объектов на прямую, нам приходится пользоваться например изображениями и подобными алгоритмами, что как то интерполировать эти характеристики

DancingOnWater
15.08.2015 20:13Т.к. исходные у вас фрактальное, то и его изображение будет фрактально подобным вплоть до каких-то масштабов. Какие именно это масштабы можно попытаться определить из вида оного.

mephistopheies
11.08.2015 14:20гугл легко с вами не согласится по поводу того полезная ли фича box-count размерность или нет, вот одна из первых ссылок


Dimcore
Все же конечно сюда зашли из-за интереса к метрикам Минковского
VtD
Нет, исключительно ради вашей дурацкой шуточки.
websurfer
Метрика метрике рознь ;-)))