1. Введение. Конкурентный корутинизм

Предыдущие статьи на тему автоматного программирования были всего лишь «цветочками». «Ягодкой» автоматного программирования, т.е. ради чего нужно им заниматься, является модель параллельных вычислений на базе модели конечных автоматов. Итак, поехали…

Стандарт С++ включил в свой состав долгожданную поддержку многопоточности [1]. Но не будем ни восхищаться этим, ни критиковать сей факт, т.к. работа с потоками отягощена таким множеством условий, оговорок и особенностей, что без реальных примеров, выявляющих проблемы многопоточности, обсуждение многопоточного программирования будет не только поспешным, но и достаточно предвзятым. Поэтому далее в основном не о потоках, а об автоматах, имея в виду, конечно, и первые.

Язык С++ далеко не первый, дополненный конструкциями параллелизма. Еще в 60-х годах прошлого столетия Н.Виртом было предложено параллельное расширение языка ALGOL [2]. Тем не менее, последующие 60 лет так и не внесли ясности в что же считать параллельным алгоритмом и какова должна быть модель параллельных вычислений. Видимо, с этим связано и столь запоздалое расширение языка С++.

Как давние конструкции языка ALGOL, так и их более современные аналоги в языке С++ представляют всего лишь структурные методы распараллеливания, которые не вводят параллельную алгоритмическую модель. В оправдание этому можно сказать, что и предпринятые за прошедшее время попытки создать подобную формальную модель вычислений потерпели фиаско. Достаточно сказать, что те же сети Петри так и не оправдали возлагавшихся на них больших надежд.

В результате «спираль» развития параллелизма вернулась, похоже, к своему истоку, претерпев лишь «терминологическое развитие». Бывшие тривиальные сопрограммы стали внезапно продвинутыми «корутинами» (калька с английского coroutine), а путаница с понятиями parallel и concurrent англоязычного сегмента параллельного программирования приводит, порой, к парадоксальным вещам. Например, первое издание книги [1] от второго отличается заменой терминов «параллельное» на «конкурентное» и «многопоточного» на «параллельное». Вот и разберись в такой ситуации «who is who».

2. Параллельная автоматная модель вычислений

Никто, наверное, уже не будет оспаривать, что следующий качественный шаг развития программирования связан с переходом к модели параллельных вычислений. Но произойдет ли это вследствие эволюционного развития существующей модели вычислений или это будет принципиально иная модель вопрос пока еще обсуждаемый. И если теоретики все еще спорят, то практически мотивированная часть программистов уже использует структурные методы распараллеливания программ.

Разделение обязанностей и повышение производительности считаются чуть ли не единственными причинами использования параллелизма. По крайней мере, к ним или их комбинации в конечном итоге сводят или пытаются свести и все остальные [1]. Но существует причина, о которой говорят редко, но из-за которой вообще стоит заниматься параллельным программированием. Ведь, скорость можно увеличить чисто аппаратными способами, а разделение обязанностей с параллелизмом связано столь же, как ежедневная работа сотрудников банка с перечнем их должностных обязанностей. И только параллельные алгоритмы — стратегия, позволяющая победить сложность решаемых задач и повысить надежность программ. И все это вопреки сложившемуся мнению в отношении многопоточного программирования, превращающего любую параллельную программу в сложный и ненадежный программный продукт.

Параллельная система, состоящая из множества параллельно функционирующих и активно взаимодействующих между собой компонент, объектов, агентов и т.п., реализует алгоритм, который определяется во многом не алгоритмами отдельных компонент (хотя и ими тоже, конечно), а количеством компонент, числом и видом связей между ними. Чтобы контролировать подобную сложность и понимать алгоритм работы параллельной системы, нужна не просто модель параллельных вычислений, а модель, имеющая, кроме всего прочего и даже прежде всего, соответствующую теорию.

Тезис о том, что «часто параллельная программа сложнее для понимания, ..., а, стало быть, возрастает и количество ошибок», мягко говоря, спорен. Да, алгоритм параллельной программы может быть достаточно сложен для понимания, но при наличии теории его можно «вычислить» формально по алгоритмам компонент. А с точки зрения проектирования, реализации и сопровождения алгоритмы компонент много проще, чем алгоритм работы системы в целом. Проектируя более простые компоненты, мы допустим явно меньше ошибок, чем проектирование системы «одним куском». Более того, отлаженные компоненты могут быть частью других систем, уменьшая сложность, повышая надежность и минимизируя издержки их проектирования.

3. Последовательный параллелизм

В статье [3] был описан параллелизм отдельной модели конечного автомата. Ее каналы на уровне исполнения переходов задают параллельное исполнение сопоставленных им функций/методов — предикатов и действий. На параллелизм предикатов при этом не накладывается ограничений. Работая, они не конфликтуют друг с другом, т.к. не влияют на содержимое памяти. Действия же, работая параллельно, могут иметь общие входные и выходные данные, а также изменять их независимо друг от друга. А все это может быть источником неопределенности значения выходных данных.

Корректность работы действий в описанных выше ситуациях обеспечивает теневая память. Сохраняя в ней новые значения, можно использовать в рамках даже одного действия одни и те же данные, как в качестве входных, так и выходных. В качестве примера можно привести модель генератора прямоугольных импульсов, описываемого как y = !y, где y — выход генератора. Его код на языке С++ в среде ВКПа представлен на листинге 1, а результаты работы программы демонстрирует рис. 1.



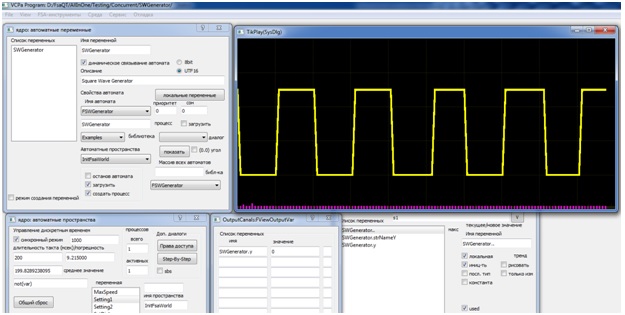
Рис. 1. Моделирование работы генератора прямоугольных импульсов в ВКПа

Автомат в данном случае имеет одно состояние с безусловным переходом (переход с прочерком на месте входного условия) в форме петли, помеченной действием y1, которое и реализует инверсию выходной переменной, формирующей в динамике прямоугольный импульс. В рамках автоматной модели частотой импульсного сигнала можно управлять, задавая значение такта дискретного времени автоматного пространства, в которое загружен автомат.

Замечание 1. В среде ВКПа автоматы загружаются в так называемые автоматные пространства, объединяющие множество автоматов. На формальном уровне каждому такому автоматному пространству соответствует сеть автоматов в едином дискретном времени. Подобных автоматных пространств в среде может быть несколько. Также разными могут быть и значения их дискретного времени.


Возможность управления дискретным временем автомата и наличие множества автоматных пространств не единственные, но важные, отличительное свойства среды ВКПа. Используя их, можно оптимизировать производительность параллельной программы. Например, автоматы, реализующие визуализацию данных и диалоги пользователя, помещать в медленные автоматные пространства, а прикладные процессы распределять по автоматным пространствам в соответствии с приоритетами и желаемой скоростью их работы и т.д. и т.п.

В рамках автоматной модели значение выхода генератора легко связать с текущим состоянием модели. Код модели генератора, имеющей уже два состояния, каждое из которых отражает состояние выхода генератора, представлен в листинге 2.


В новой модели состояния заменяют выходную переменную, а это, как можно видеть, резко упростило модель генератора. В результате мы получили «голый» автомат, представленный только таблицей переходов. Для отслеживания его текущего состояния «s1» в ВКПа для автомата с именем SWGenState создана переменная типа fsa(state) с именем SWGenState.(s1). Она принимает истинное значение в состоянии s1, и ложное, когда автомат находится в другом состоянии. Далее эта переменная используется уже средствами отображения данных среды ВКПа (см. тренд сигнала на рис. 2).


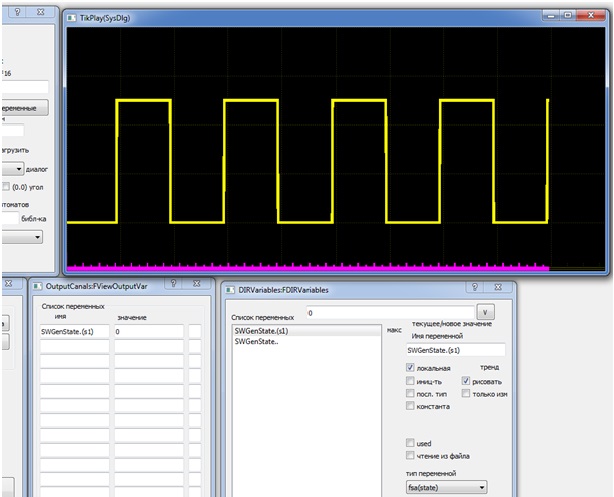
Рис. 2. Моделирование генератора на состояниях

4. Модель управления параллельных вычислений

Далее, двигаясь в сторону создания модели параллельных процессов, логично использовать множество одновременно функционирующих и взаимодействующих конечных автоматов, т.е. сеть автоматов. При этом появляется проблема выбора модели времени сети, которое может быть единым для всех автоматов или в пределе индивидуальным у каждого. В ВКПа выбор сделан в пользу единого времени (подробнее о синхронных сетях автоматов см. [5]).

Выбор единого времени позволяет создать алгебру автоматов, имеющую операции композиции и декомпозиции автоматов. С помощью первой можно найти результирующий автомат, который дает точное представление о работе параллельной системы. И тут стоит вспомнить приведенный выше тезис о «сложности понимания» параллельных программ. Наличие операции композиции позволяет решить «проблему понимания» работы параллельной программы.

Безусловно, результирующий автомат для сети из большого числа компонент может быть весьма объемным. Но, к счастью, чаще требуется понимание работы подсистем или сетей из небольшого числа компонент, для которых нахождение результирующего автомата не вызывает больших проблем. Рассмотренный далее пример модели RS-триггера это демонстрирует.

Модель RS-триггера является примером простейшей параллельной системы. Особенно она интересна наличием перекрестных обратных связей. Обратные связи, или, по-другому, циклические цепи, петли, алгебраические петли (algebraic loop) и т.п. являются на текущий момент серьезной проблемой для структурных моделей параллельных систем. В общем случае она разрешается введением в разрыв петель элементов памяти. Это стандартное решение, предлагаемое теорией автоматов [4]. Такой же выход рекомендуется и в лице MATLAB. Среда ВКПа отличается тем, что ей для реализации петель не требует введения подобных дополнительных элементов. Заметим, а это очень важно, реальные схемы также в них не нуждаются (см. схему RS-триггера).

На рис. 3 представлена простейшая модель элемента И-НЕ, из которых состоит схема RS-триггера. Она не учитывает задержки элемента, а также их тип (транспортные или инерционные задержки). Тем не менее, как минимум один такт задержки она все же содержит. Это время перехода из одного состояния в другое. Код модели демонстрирует листинг 3.


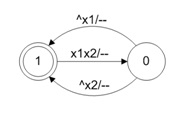
Рис. 3. Модель элемента И-НЕ


На рис. 4 показана схема RS-триггера и его модель в форме конечно-автоматной сети. Стрелками на модели обозначены связи между автоматами сети. Здесь, с одной стороны, состояния моделей отражают состояния выходов элемента, а, с другой стороны, они же используются в качестве сигналов для организации информационных связей между параллельными процессами. Именно такая форма модели (с синхронизацией через состояния) позволяет достаточно просто найти результирующий автомат сети. Он показан на рис. 5 (о процедуре нахождения результирующего автомата подробнее см. [6]).

Сравните [результирующий] алгоритм работы параллельной программы RS-триггера и алгоритм работы отдельного элемента И-НЕ. Разница разительная. При этом алгоритмы компонент созданы «ручками», а алгоритм параллельной системы создается неявным образом — «искусственным интеллектом» сети. Вот в чем качественное отличие параллельных программ от последовательных: изменив только связи (хотя бы одну), мы получим уже совершенно другой алгоритм работы. И это будет уже точно не RS-триггер. И, кстати, другой результирующий автомат.


Рис. 4. Схема RS-триггера и его сетевая модель


Рис. 5. Результирующий автомат сетевой модели RS-триггера

Анализ результирующего автомата на рис. 5 дает следующее «понимание» работы параллельной программы (и реального триггера, конечно). Во-первых, при переходе из одного состояния в другое триггер обязательно перейдет через «запрещенное» состояние выходов (а что по этому поводу утверждают учебники?). Во-вторых, если загнать триггер в единичное состояние выходов (в состояние «s1w1»), а затем на входы подать две единицы, то он войдет в режим генерации, т.е. циклическое переключение между состояниями «s1w1» и «s0w0» и (а о генерации триггера вы слышали?).

Переход через запрещенное состояние происходит и у реального триггера, а вот режим генерации невозможен из-за различия задержек у реальных элементов. Рис. 6 демонстрирует режим генерации программной модели триггера, который существует до тех пор пока сохраняются единицы на входах.

Замечание 2. Типовое описание работы RS-триггера дается в подавляющем числе случаев в форме таблицы истинности. Но поступать так, понимая, что триггер — это последовательностная схема, это, по сути дела, сознательно вводить в заблуждение изучающих эту тему. Ну, нет и не может быть у триггера «запрещенных состояний»! Но почему-то лишь единицы решаются открыть эту истину и уж, тем более, обсуждать проблему его генерации (см. например, [7]).


Рис. 7 демонстрирует переключение модели триггера между его устойчивыми состояниями. Здесь уже единичное состояние входов триггера сохраняет текущее состояние выходов триггера, а при установке в ноль того или иного входа происходит переключение в противоположное состояние. При этом при переключении триггера его выходы на момент, равный одному дискретному такту, принимают одновременно единичное (кем запрещенное?) состояние.


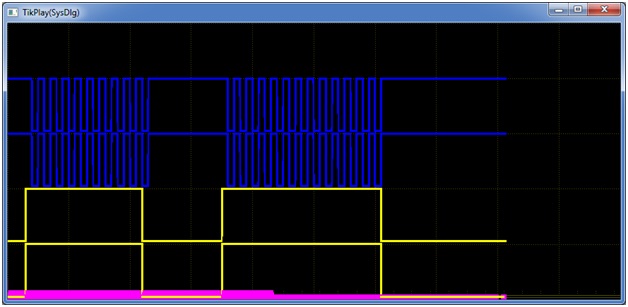
Рис. 6. Режим генерации RS-триггера


Рис. 7. Переключение RS-триггера между состояниями

Рассмотрим еще одну модель RS-триггера, состоящую из одного состояния и одного действия, т.е. аналогичную модели на листинге 1. Ее код демонстрирует листинг 4. У данной модели, как и у модели генератора, нет предикатов и значения сигналов без каких-либо промежуточных преобразований являются входными данными действия y1. Хорошо это или плохо? С одной стороны, кажется, что хорошо, т.к. код стал проще, но, с другой стороны,… не очень. А в причинах этого мы сейчас и разберемся.


Если мы протестируем новую модель в режиме «теневой памяти», то не увидим каких-либо отличий ее работы от предыдущей, т.е. и, переключаясь, она будет проходить через запрещенные состояния и исправно входить в режим генерации. Если же мы установим работу с данными в обычном режиме, то получим результаты, показанные на рис. 8 и рис. 9.


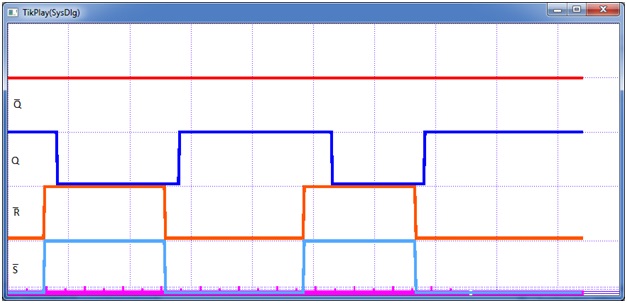
Рис. 8. Срыв режима генерации у модели RS-триггера


Рис. 9. Пропуск запрещенных состояний моделью RS-триггера

Почему первая модель вне зависимости от режима работы с памятью демонстрирует стабильные результаты работы, а вторая — изменяет поведение? Причина в предикатах. У второй модели предикатов нет и это является критичным для ее поведения. Но как и почему наличие/отсутствие предикатов влияет на алгоритм работы параллельной программы?

У программной модели элемента И-НЕ, как у автоматной программы, есть два входных канала и один выходной. Им должны быть сопоставлены два предиката и одно действие. Первая программа этому полностью соответствует. Ядро ВКПа, интерпретирующее автоматное описание, сначала исполняет все предикаты не только отдельного автомата, но и всего автоматного пространства, и только затем запускает все действия. В этом случае, в какой бы последовательности действия не исполнялись, имитируя параллелизм, и в каком бы режиме с памятью они не работали, результаты предикатов на текущем такте работы автомата от них (действий) не зависят. Потому-то первая программа выдает один и тот же результат.

Вторая программа, хотя работает с входными каналами автомата напрямую — считывает входные сигналы в рамках действия. Действия, работая с входными данными в режиме теневой памяти, записывают новые значения в теневую же память и тем самым работают с данными, действительными на начало дискретного такта. В обычном же режиме они «хватают» мгновенные значения, установленные в момент их изменения, и тем самым алгоритм попадает в зависимость от моментов изменения памяти. Подобную зависимость и демонстрирует вторая программа. И даже если бы ввели во вторую модель методы-предикаты это ни как не повлияло бы на результаты ее работы. Здесь важен не сам факт наличия методов-предикатов, а особенности их работы в рамках модели автоматного программирования.

5. Выводы

На примере параллельной программы RS-триггера мы рассмотрели некоторые свойства, присущие любым параллельных программ. Мы и далее на примере логических (цифровых) схем будем рассматривать те или иные общие аспекты функционирования параллельных программ. Выбор темы моделирования цифровых схем здесь не случаен. Они фактически в «рафинированном виде» представляют работу параллельных процессов. Это делает разбор нюансов параллелизма, гонки, синхронизация, тупики и т.д. и т.п., прозрачным, ясным и простым.

При этом, как бы вы не называли программирование — «конкурентным» или параллельным, используете ли вы для программирования «корутины», сопрограммы, потоки или автоматы, результат работы [параллельной] программы должен быть во всех реализациях один и тот же. Автоматная модель параллельных программ в рамках ВКПа преследует эту и только эту цель.
Какие бы не делались предположения по поводу реализации ядра интерпретации автоматов среды ВКПа все это будут «домыслы», т.к. результат работы автоматных программ не должен быть связан с реализацией вычислительной модели. Она может быть программной (как сейчас) или аппаратной (как, надеюсь, в будущем), реализованной на одном ядре или на их множестве, в однопоточном или многопоточном варианте и т.д. и т.п. все это никак не должно влиять на результаты работы параллельных автоматных программ.

И, похоже, поставленной цели удалось добиться. Модель RS-триггера, как один из возможных тестов систем на параллелизм [8], в этом убеждает… Как показала жизнь, все остальные параллельные программы, при условии успешного прохождения средой реализации параллелизма теста RS-триггера, работают столь же корректно, надежно и стабильно. Кстати, тот же MATLAB «тест RS-триггера» не прошел, а это говорит уже о многом…