Интегральное изображение ― алгоритм, позволяющий эффективно вычислять сумму значений, заключенных в прямоугольном подмножестве многомерного массива. Сама его идея восходит к исследованиям многомерных функций распределения вероятностей, и до сих пор он находил успешное применение в тех областях, которые непосредственно используют теорию вероятностей в качестве основного инструментария. Например, в распознавании образов.

Сегодня мы рассмотрим любопытный случай, как применить интегральные изображения в кардинально другой сфере ― вычислительной физике. А именно ― посмотрим, что будет, если вычислить с их помощью центр масс поля импульсов, и какую выгоду можно извлечь из этого симбиоза.

В этой статье я расскажу:

• Что за задача такая, о которой идет речь;
• Подробнее об интегральных изображениях;
• Как использовать интегральные изображения для приближенного решения гравитационной задачи N тел применительно к дискретному полю импульсов (масс-скоростей);
• Какой недостаток имеет это решение и как его исправить;
• И, наконец, как за константное время вычислить центр масс для произвольного региона.

Гравитационная задача N тел

Строгое решение гравитационного взаимодействия системы из N тел относится к алгоритмам, имеющим квадратичную сложность: на каждое из тел оказывают гравитационное воздействие все остальные тела в системе^[1]. Следовательно, силу гравитационного взаимодействия нужно посчитать для каждой из N²/2 пар.

Чтобы проиллюстрировать, насколько трудоемко строгое решение, можно попробовать соотнести сложность расчета реальной системы с показателями быстродействия современных компьютеров.

Для вычисления силы тяготения между двумя телами в трехмерном пространстве необходимо выполнить 20 операций с плавающей точкой (FLOP). В Солнечной системе насчитывается около 100 тел размером более 200 километров (включая Солнце, 9 планет, карликовые планеты и спутники)^[2]. Приблизительное число астероидов на околоземной орбите составляет около 20 тысяч^[3]. В поясе астероидов насчитывается от 1,1 до 1,9 миллионов тел размером больше 1 км^[4] и порядка одного миллиона астероидов похожего размера в «троянской»^[5] и «греческой» группах Юпитера. В поясе Койпера порядка 100 миллионов объектов размером более 20 км^[6] и еще около 2 триллионов ― в облаке Оорта^[7].



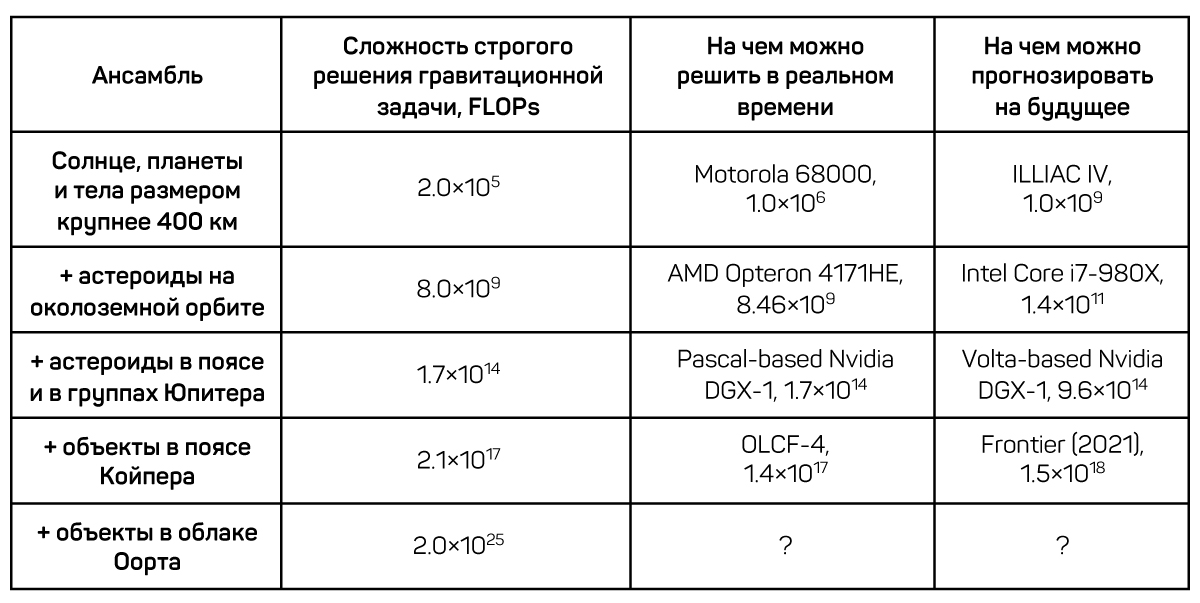
Вычислительная мощность, требуемая для строгого решения последней гравитационной задачи, всего на порядок меньше вычислительной мощности, требуемой для симуляции работы человеческого мозга на нейронном уровне (2,5×10²⁶)^[8]. Именно поэтому ее строгое решение обычно заменяется приближенным.

Один из наиболее широко используемых алгоритмов для приближенного решения гравитационной задачи ― Tree Code ― имеет квазилинейную временную сложность O(N*logN)^[9]. Tree Code строит пространственное дерево и для каждого узла в этом дереве рассчитывает общую массу и центр масс всех тел, которые в него попадают. В дальнейшем, при расчете гравитационных сил, действующих на каждое тело, Tree Code может учитывать не прямое влияние других тел, а влияние узлов дерева, причем в зависимости от дистанции он выбирает все более крупные узлы, которые содержат параметры все более многочисленного подмножества тел.


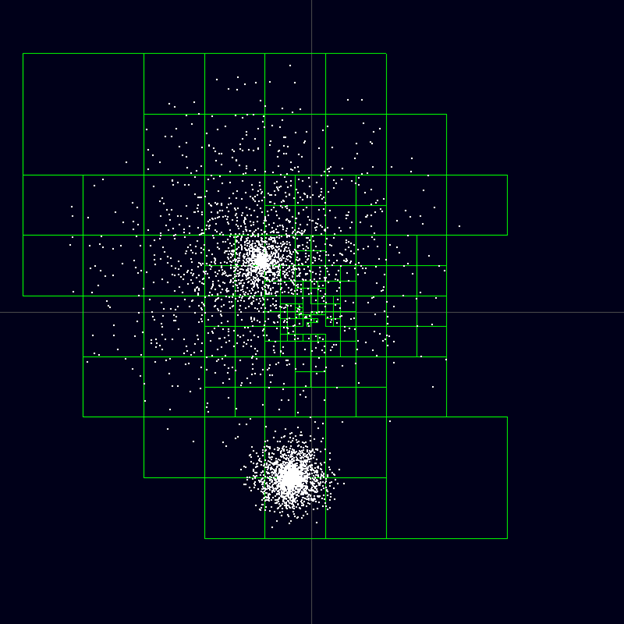
Иллюстрация из Википедии. На тело в центре действуют массы узлов, обозначенных зелеными прямоугольниками. Напрямую учитываются только массы ближайших тел

Гравитационная задача для поля импульсов

Поле импульсов ― это дискретное векторное поле mv(p), которое каждой точке рассматриваемого пространства p ставит в соответствие пару масса-скорость. Поле импульсов можно задать для пространства любой размерности. Пара масса-скорость характеризует количество движения и представляет собой вектор размерностью R + 1, где R ― размерность пространства, для которого задано поле импульсов. Например, для R = 2 это может быть вектор {v_x, v_y, m}.

Стоит отметить, что математически традиционный вариант описания этой системы ― комбинация векторного поля скоростей и скалярного поля масс. В данном случае мы позволяем себе вольность комбинировать скорость и массу в одном векторе, поскольку не претендуем на математическую значимость.


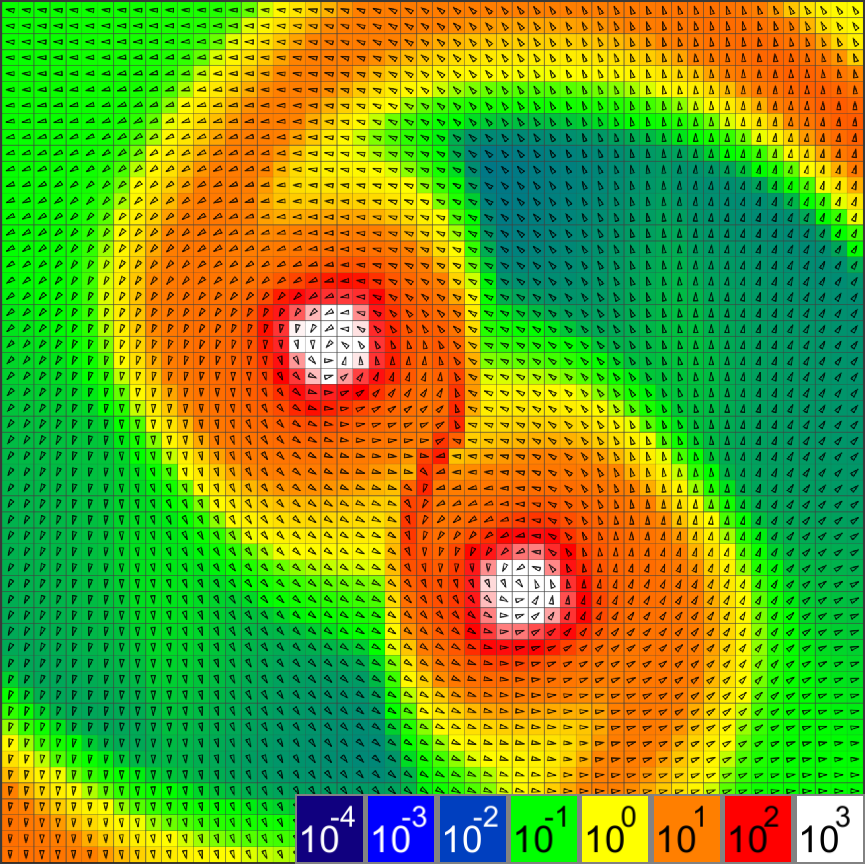
Небольшой участок векторного поля импульсов: массы обозначены цветом, направления ― стрелками


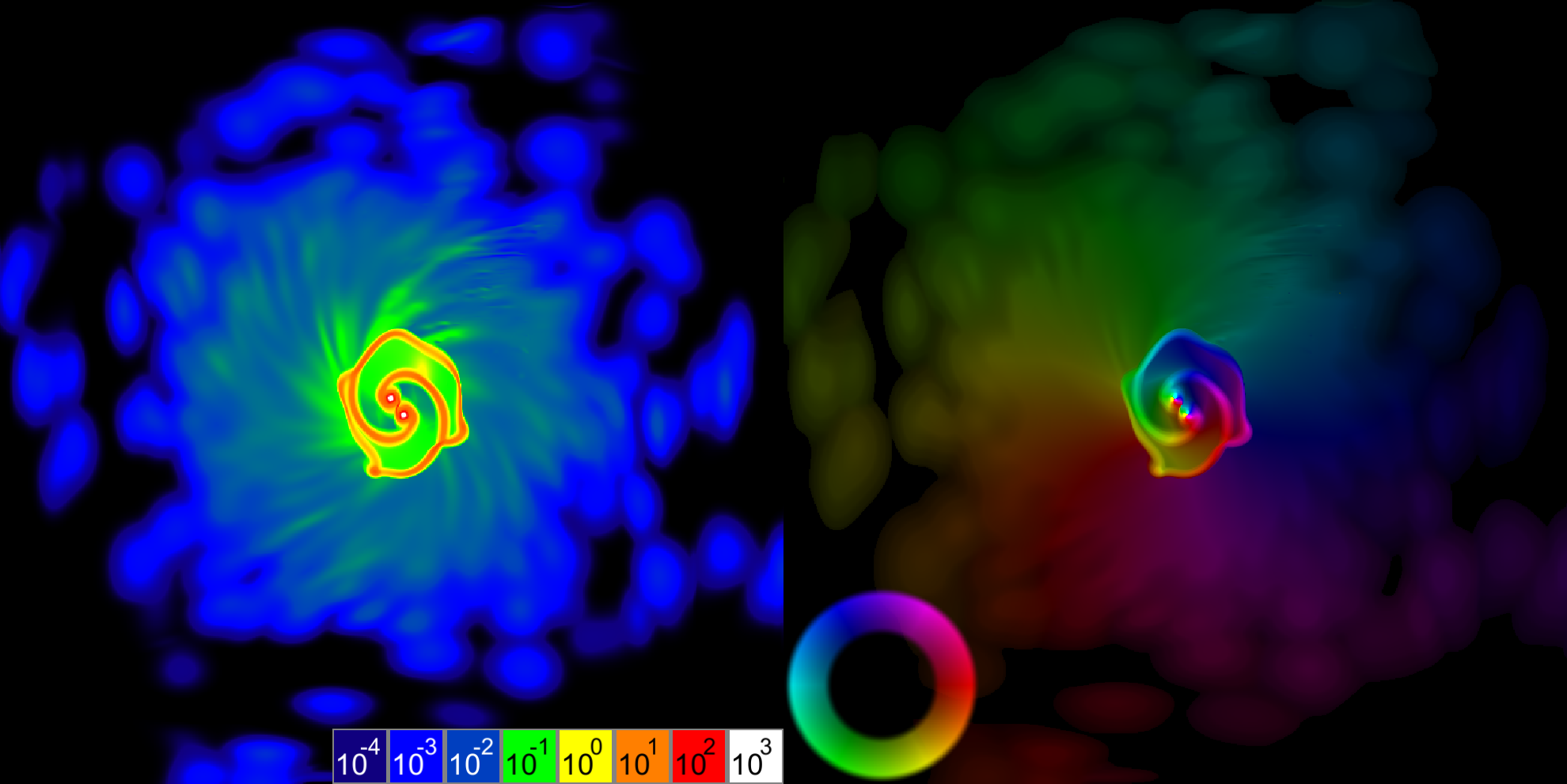
Векторное поле импульсов размером 729×729 элементов. Слева ― массы. Справа ― импульсы. Импульсы на этой иллюстрации закодированы цветом в формате HSV (Hue ― направление импульса, а Value линейно отображает порядок его абсолютной величины таким образом, что наименее различимы (Value = 0,05) импульсы порядка 10^-7, а самые яркие импульсы (Value = 1,0) имеют порядок 10³ и выше).

Подобные этому ― сеточные ― методы описания физических систем повсеместно используются в астрофизике для моделирования эволюции газовых облаков, формирования звезд и галактик. К ним относятся метод SAMR^[10] или сеточная модель гидродинамики^[11].

Как и в случае гравитационной задачи N тел, алгоритму эволюции дискретного поля необходимо учесть гравитационное влияние всех масс, составляющих это самое поле, на каждый его дискретный элемент. При этом необходимо принимать во внимание, что сложность задачи косвенно зависит от размерности пространства R: например, для поля на плоскости, состоящего из 1000×1000 элементов, общее число N составит 10⁶ элементов, а поле такого же размера в трехмерном пространстве будет включать в себя уже 10⁹ элементов.

Тем не менее, существует ряд приемов, позволяющих приближенно решить гравитационную задачу и для поля импульсов. Метод Multigrid использует иерархическую дискретизацию, поддерживая несколько сеток различного размера^[12]. Multipole Expansion трактует группы источников, расположенные близко друг к другу, как один объект^[13]. Multigrid имеет квазилинейную вычислительную сложность и логарифмическую сложность по памяти. Один из вариантов Multipole Expansion ― FMM ― демонстрирует линейную вычислительную сложность в обмен на пониженную точность вычислений^[14].

Ниже мы рассмотрим еще один метод, позволяющий решить гравитационную задачу для дискретного поля импульсов за квазилинейное время и обладающий линейной сложностью по памяти.

Интегральное изображение

Интегральное изображение дает посчитать за константное время сумму элементов оригинального изображения в произвольной прямоугольной области^[15]. В компьютерной графике интегральные изображения первоначально были предложены в качестве альтернативы мипмаппингу и анизотропной фильтрации^[16]. Кроме того, они успешно используются для цифровой обработки изображений и в методиках распознавания образов.

Интегральное изображение ― один из самых наглядных примеров компромисса между вычислительной сложностью и сложностью по памяти. «Наивный» алгоритм подсчета суммы элементов изображения обладает временной сложностью O(M*N) и сложностью по памяти O(1). Интегральное изображение позволяет совершать те же вычисления за время O(1) и обладает сложностью по памяти O(M*N).


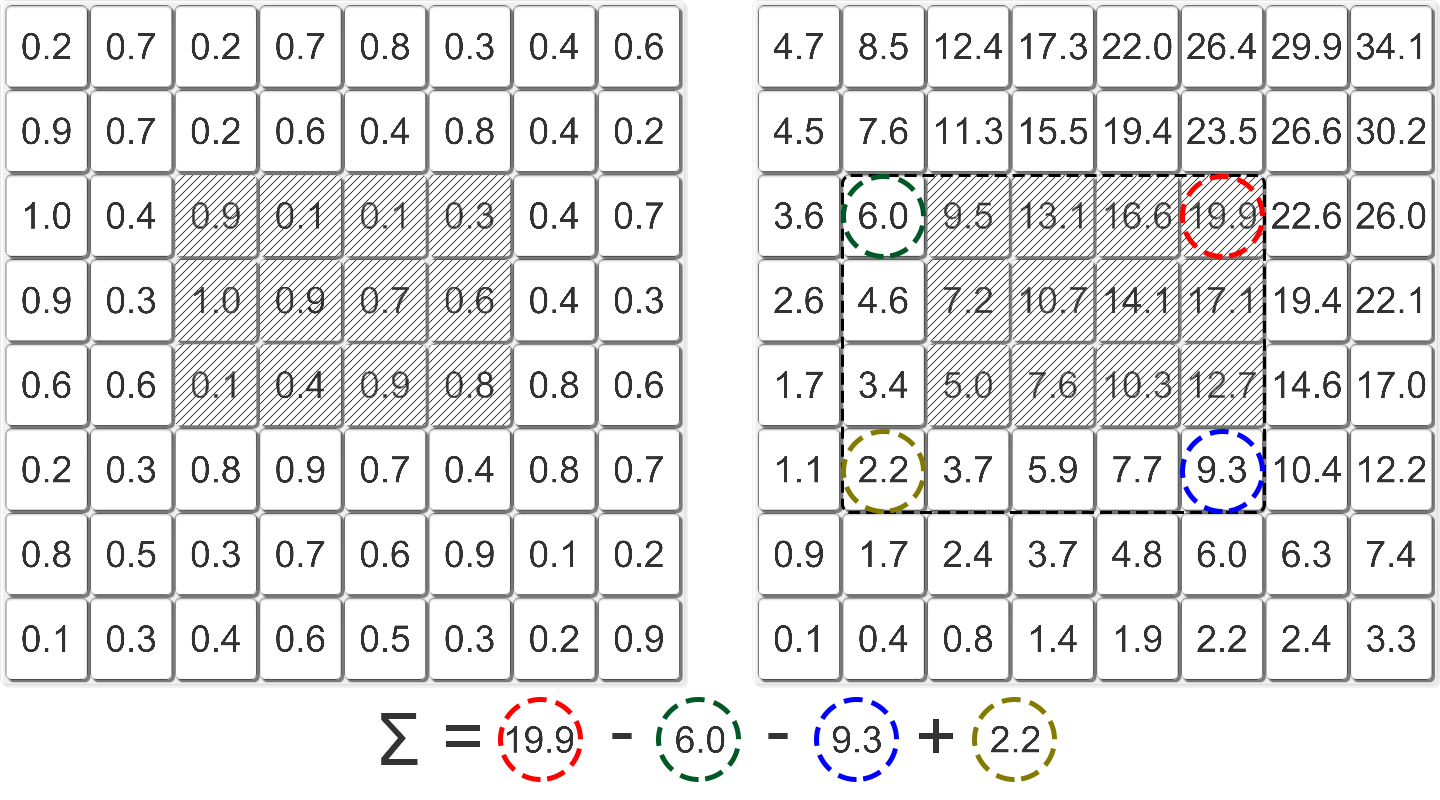
Использование интегрального изображения для вычисления суммы элементов в заданном регионе

Алгоритм расчета интегрального изображения очень прост, характеризуется линейной вычислительной сложностью и легко параллелизируется под GPGPU^[17]. Реализуется он подобно двухпроходному фильтру Гаусса^[18]: в первом проходе считаются частные суммы для строк, во втором эти частные суммы аккумулируются по столбцам.


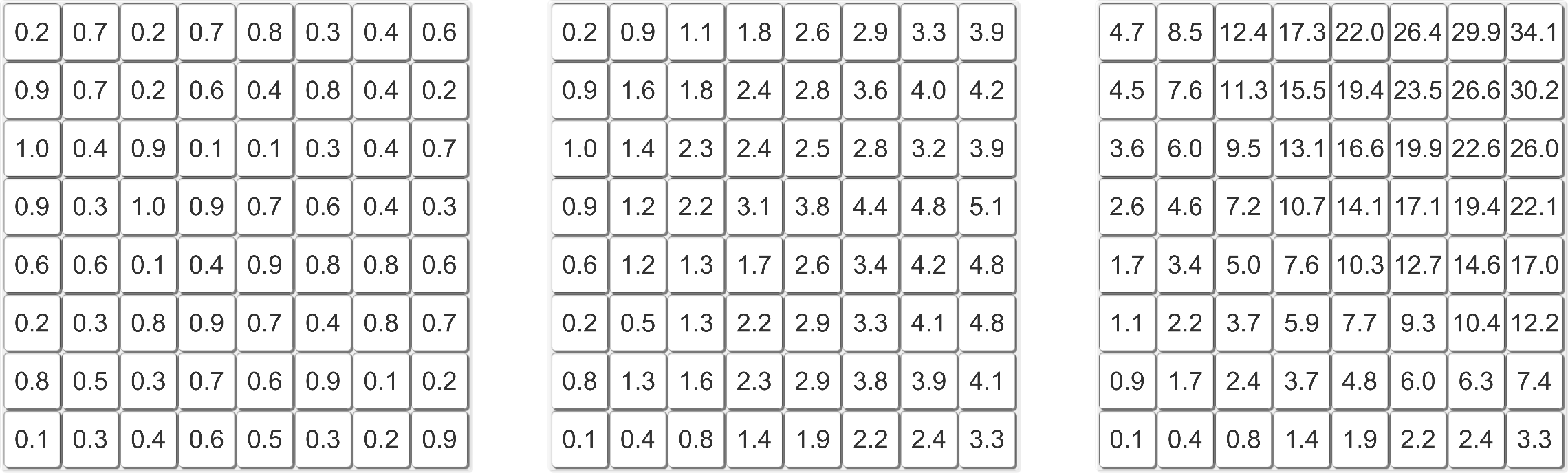
Вычисление интегрального изображения в два прохода. Слева ― оригинальное изображение. В центре ― частные суммы для строк. Справа ― итоговое интегральное изображение.


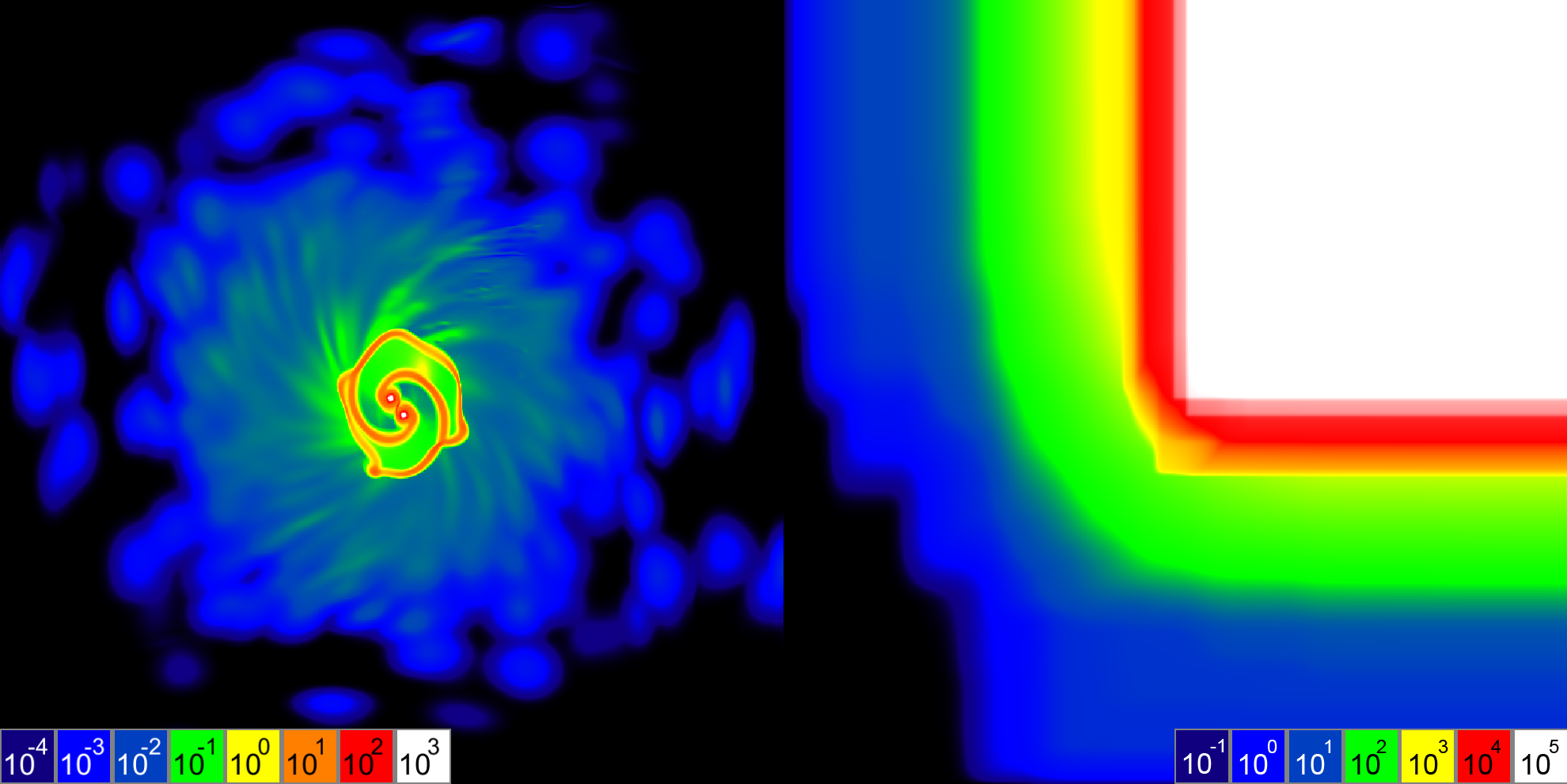
Слева ― изображение, содержащее массы элементов. Справа ― его интегральное изображение. Изображения слева и справа используют разные логарифмические шкалы.

Приближенное решение гравитационной задачи с помощью интегрального изображения

Имея в своем распоряжении интегральное изображение масс, несложно адаптировать под нее методику, характерную для Tree Code и Multipole Expansion. Так, для каждого элемента дискретного поля:

1. Непосредственно учитываем влияние масс только соседних восьми элементов;
2. Учитываем влияние восьми соседних регионов, состоящих из девяти элементов (3×3), путем вычисления суммы их масс с помощью интегрального изображения;
3. На каждом последующем шаге увеличиваем размер региона в 3 раза (9×9, 27×27, 81×81, и т.д.) до тех пор, пока этот он не превысит размер всего векторного поля.

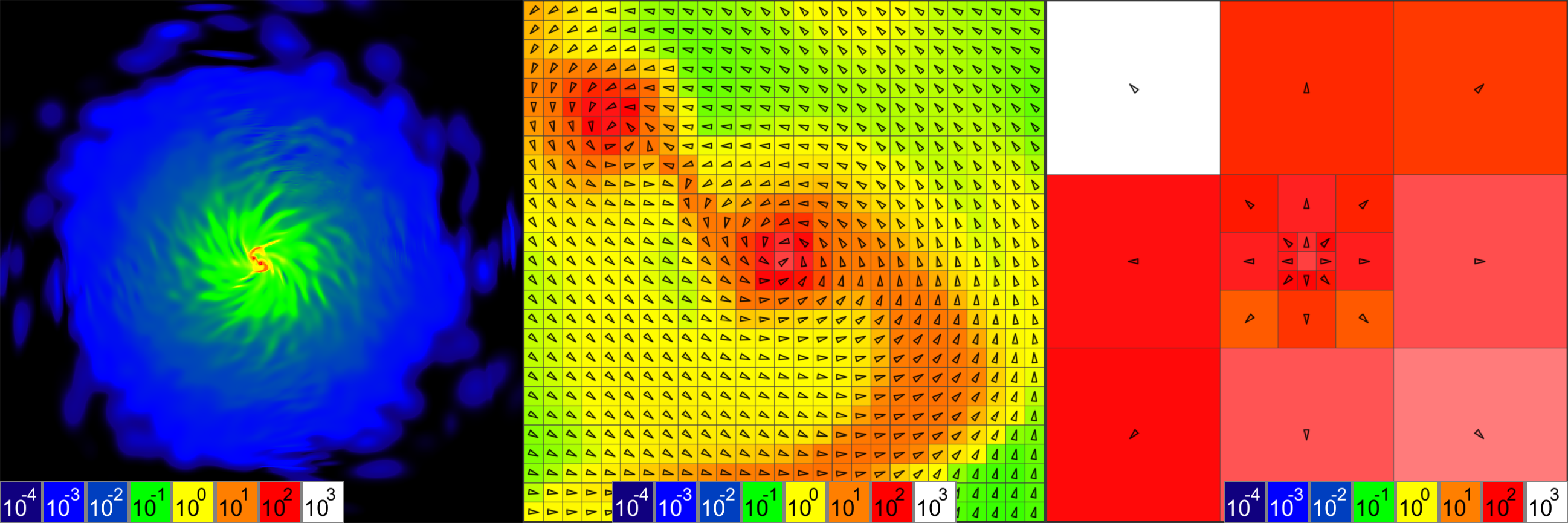
Приближенный расчет сил, действующих на элемент векторного поля импульсов, с помощью интегрального изображения масс

Сложность приближенного решения гравитационной задачи для поля импульсов с помощью интегрального изображения растет квазилинейно, как O(N*8*log3(sqrt(N))) для R = 2 и как O(N*26*log3(cbrt(N))) для R = 3.



Однако в таком виде это решение обладает тем же недостатком, что и методика Multigrid, а именно ― ощутимой дискретной «ригидностью» низкочастотных компонентов функции гравитации. Проще всего продемонстрировать эту проблему наглядно.


Силы на этой иллюстрации закодированы цветом в формате HSV (Hue ― направление силы, Value линейно отображает порядок его абсолютной величины таким образом, что наименее различимы (Value = 0,05) силы порядка 10^-7, а самые яркие силы (Value = 1,0) имеют порядок 10³ и выше).

На иллюстрации выше невооруженным глазом заметен эффект «ригидности» низкочастотных компонентов функции гравитации. Но если в Multigrid эта «ригидность» происходит из-за снижения частоты дискретизации, то в интегральном изображении это связано с отсутствием информации о характере пространственного распределения масс. Дело в том, что алгоритм, который аппроксимирует силы с помощью интегрального изображения, считает, что центр масс совпадает с центром региона.


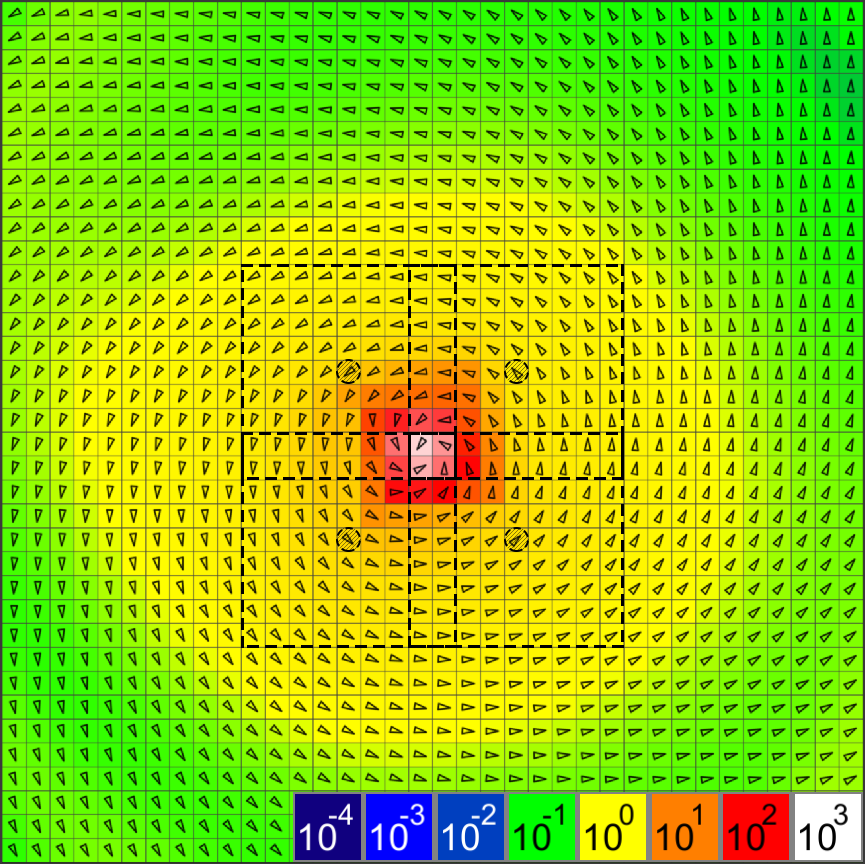
В центре иллюстрации показан экстремум масс при сравнительно равномерном распределении массы в остальном поле

Экстремум масс попадает в каждый из четырех прямоугольных регионов. Очевидно, что позиция центра масс каждого региона должна примерно совпадать с элементом, обозначенным белым цветом, масса которого на три порядка больше массы большинства элементов региона, обозначенных желтым цветом. Однако в расчетах низкочастотных компонентов функции гравитации для этих регионов считается, что центры их масс совпадают с центрами регионов, обозначенными окружностями.

Решить эту проблему можно, внедрив в интегральное изображение дополнительную информацию, которая даст возможность вычислять не только сумму масс в заданном регионе, но и координаты центра масс.

Для начала попробуем представить себе изображение, каждый элемент которого содержит свои собственные координаты. Соответствующее ему интегральное изображение будет содержать суммы координат. Следовательно, сумма произвольного региона этого интегрального изображения, разделенная на общее число элементов этого региона, будет равна координатам центра этого региона.


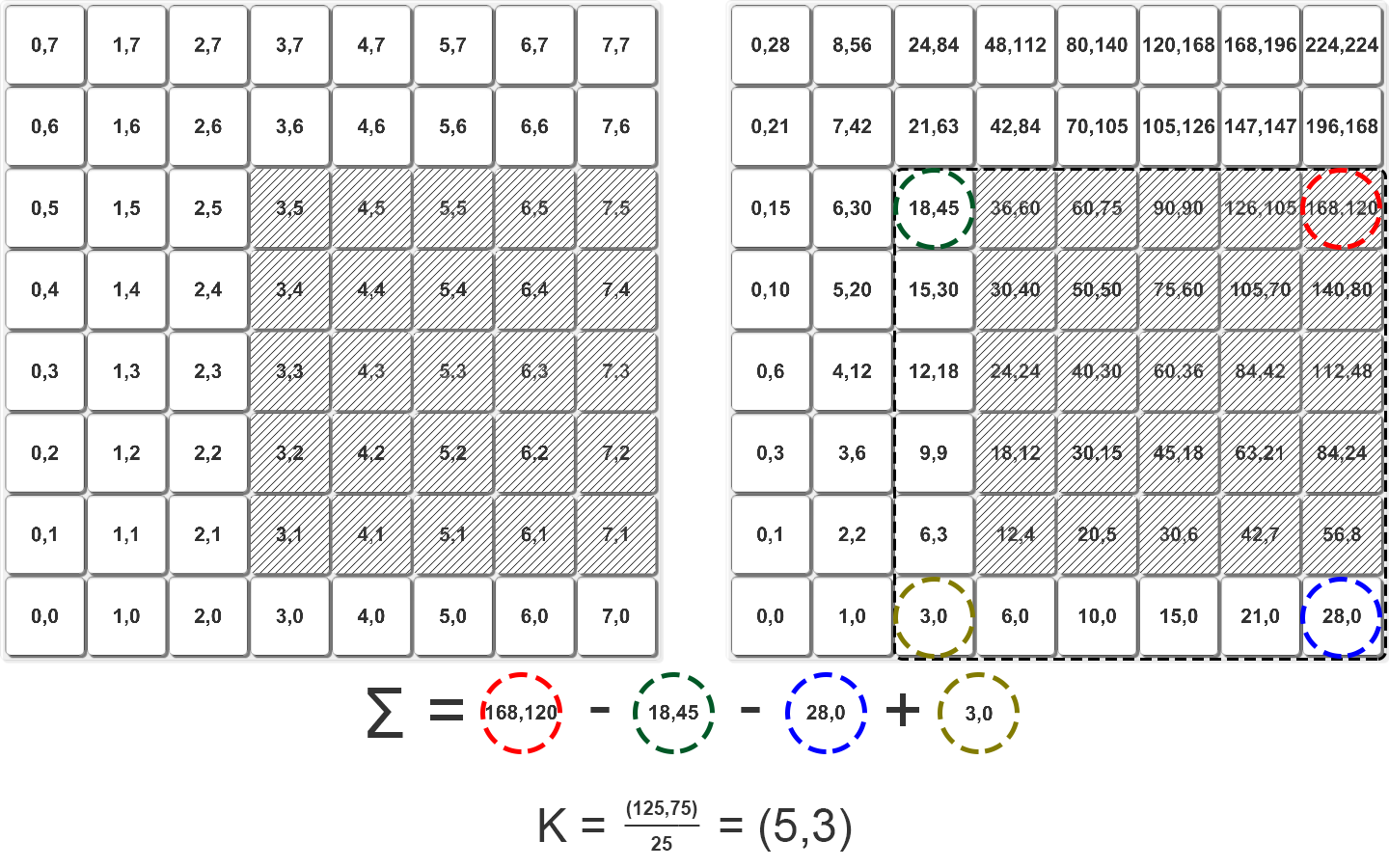
Интегральное изображение координат

Возьмем для примера регион в левом нижнем углу с координатами {3; 1} и в верхнем правом с координатами {7; 5}. Сумма координат этого региона {168; 120} ― {18; 45} ― {28; 0} + {3; 0} равна {125; 75}, общее число элементов равно 25, следовательно, координаты его центра будут {5; 3}.

Все, что осталось сделать, ― обобщить этот частный случай, в котором мы считаем, что все элементы изображения обладают одним и тем же весовым коэффициентом, равным единице. Чтобы учесть разные весовые коэффициенты, мы будем домножать на них координаты элементов. А взвешенные координаты центра региона мы получим, если разделим сумму взвешенных координат на сумму весовых коэффициентов.


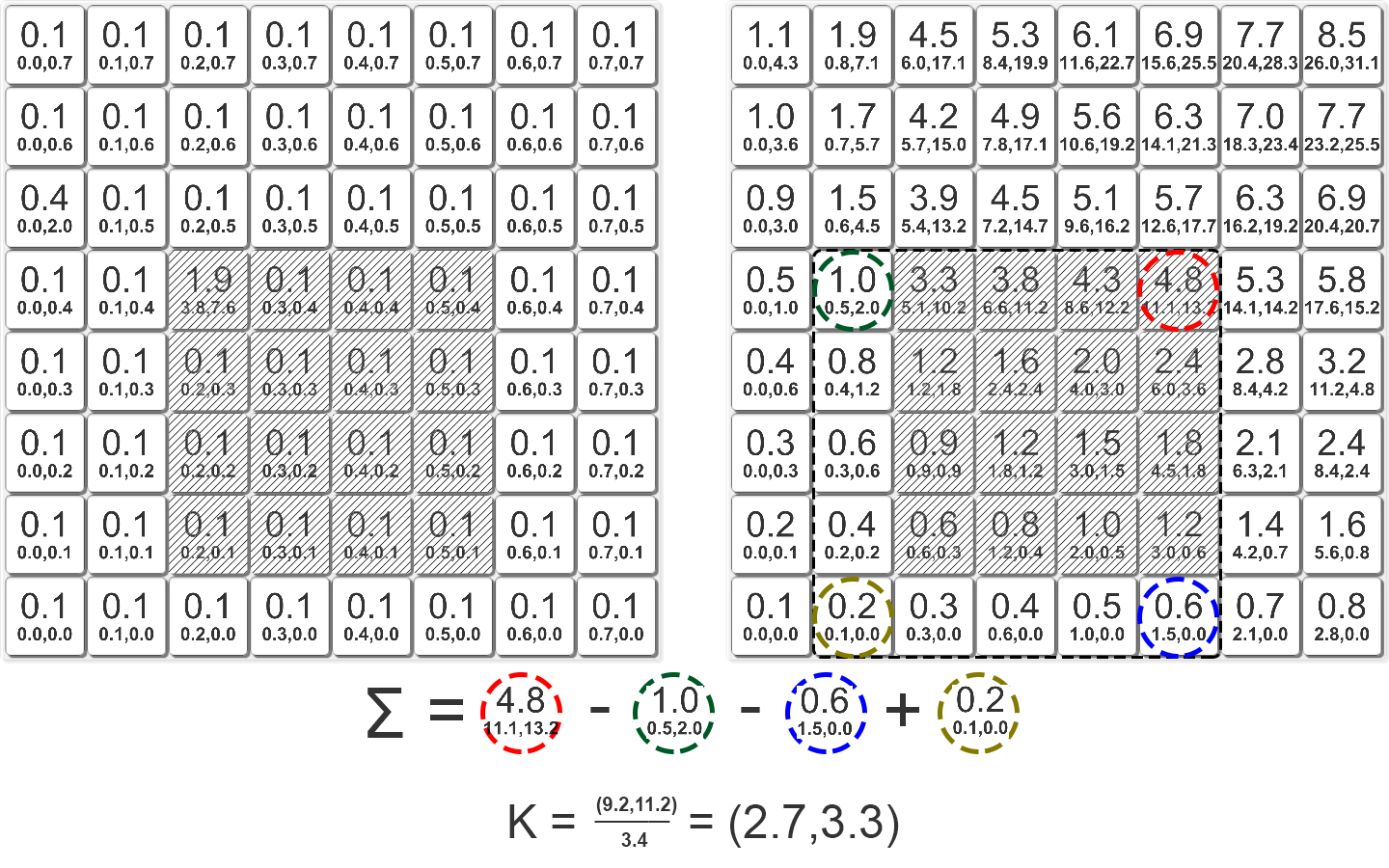
Интегральное изображение взвешенных координат. Увеличенным шрифтом обозначены весовые коэффициенты

Рассмотрим регион в левом нижнем углу с координатами {2; 1} и в правом верхнем с координатами {5; 4}. Сумма весовых коэффициентов этого региона 4,8 ― 1,0 ― 0,6 + 0,2 равна 3,4, а сумма его взвешенных координат {11,1; 13,2} ― {0,5; 2,0} ― {1,5; 0,0} + {0,1; 0,0} равна {9,2; 11,2}. Таким образом, взвешенные координаты центра этого региона равны {2,7; 3,3}.

Убедиться в том, что эта схема действительно работает, можно наглядно ― преобразовав интегральное изображение со взвешенными координатами в distance field с помощью distance transform^[19].


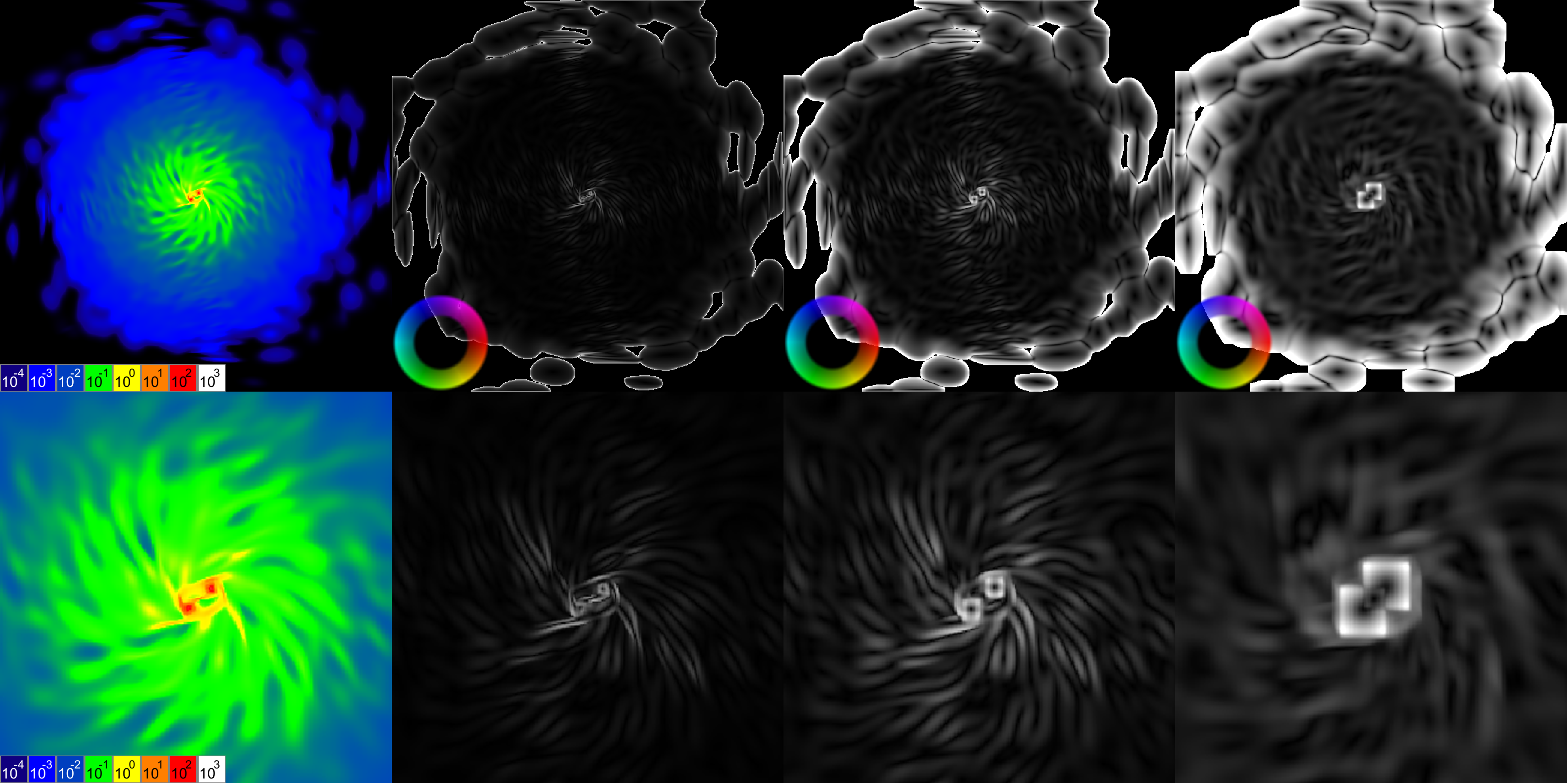
Преобразование интегрального изображения со взвешенными координатами в distance field. Слева ― изображение масс. Следующее изображение ― дистанция до центра масс для региона размером 3×3 элемента. Далее ― дистанция до центров масс для регионов размерами 9×9 и 27×27 элементов. Величины дистанций на этой иллюстрации нормализуются к размеру региона, используемого для выборки.


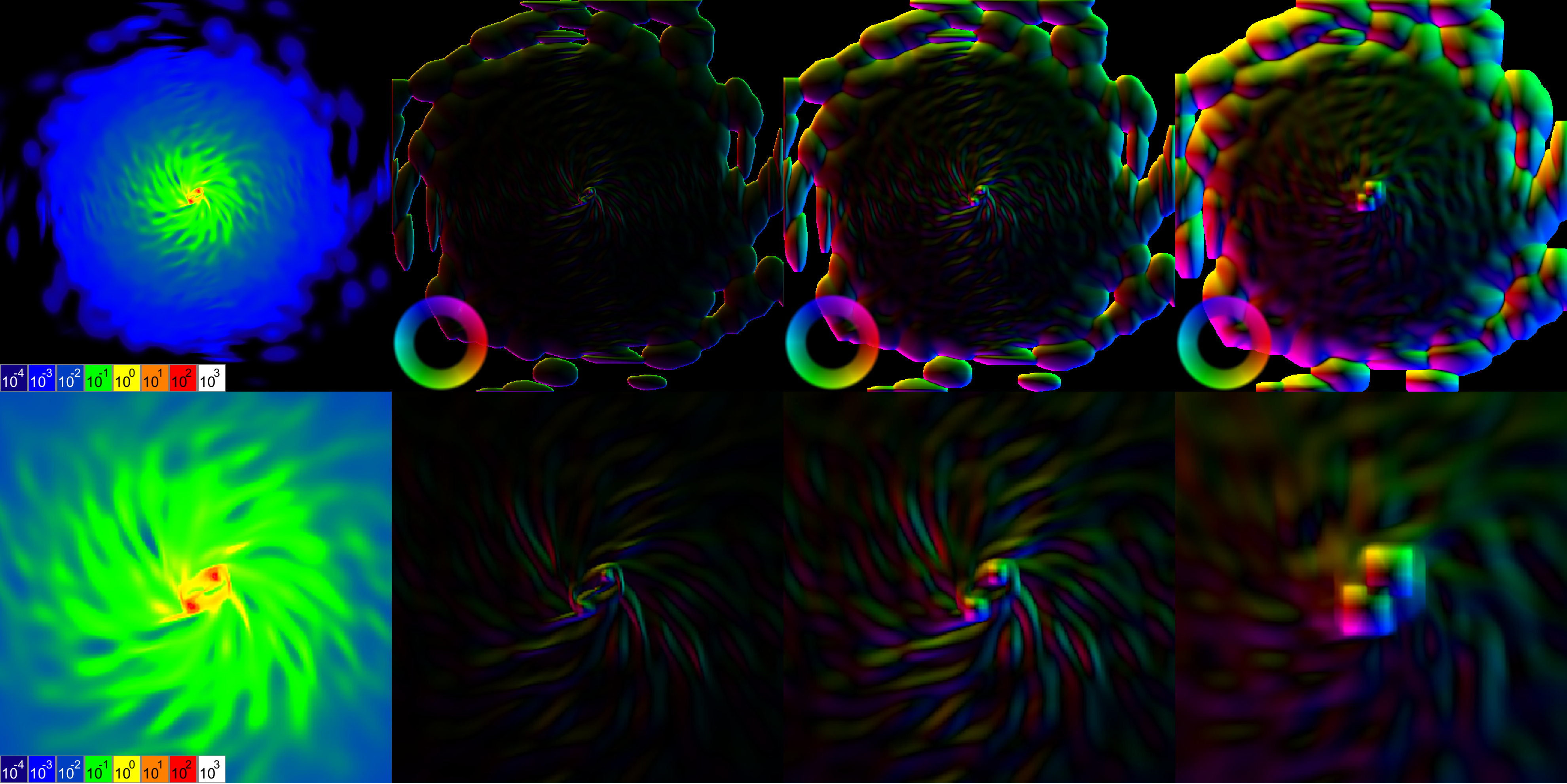
Преобразование интегрального изображения со взвешенными координатами в directed distance field. Направление и дистанция закодированы цветом в формате HSV, где Hue ― направление, Value ― нормализованная дистанция. Величины дистанций на этой иллюстрации нормализуются к размеру региона, используемого для выборки.

Суммируя все вышеизложенное:

1. К исходному изображению масс, используемому для вычисления интегрального изображения, добавляется еще два (или три, если R = 3) компонента ― взвешенные координаты элемента, равные координатам, умноженным на массу.
2. Координаты центра масс произвольного региона вычисляется путем деления суммы его взвешенных координат на сумму его масс.
3. Вычисление центра масс региона имеет константную вычислительную сложность O(1).
4. Сложность по памяти для интегрального изображения со взвешенными координатами остается линейной O(M*N).

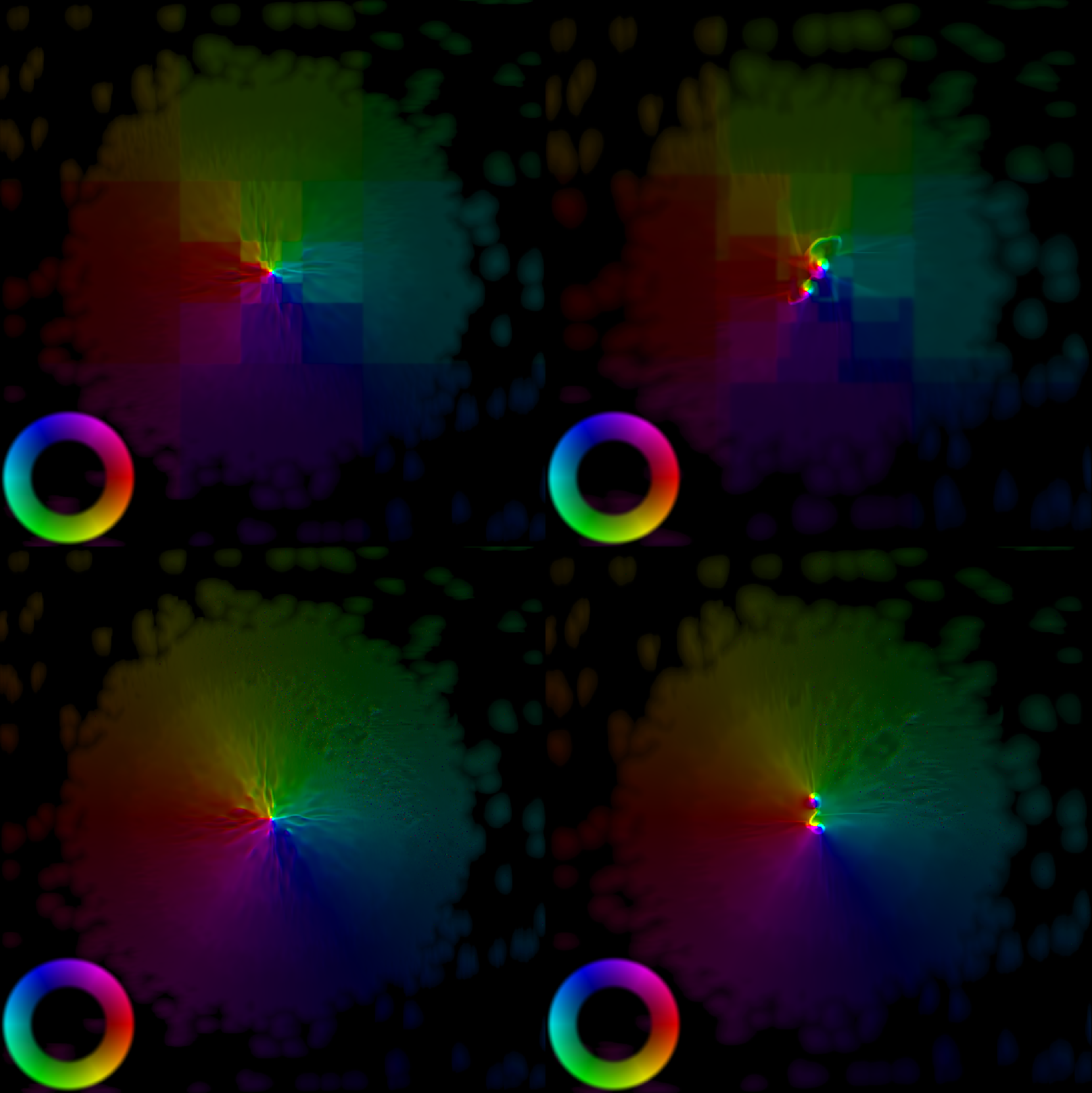
Сравнение методов аппроксимации функции гравитации. Сверху ― для аппроксимации используется интегральное изображение без взвешенных координат. Снизу ― для аппроксимации используется интегральное изображение со взвешенными координатами.

Численная устойчивость интегральных изображений со взвешенными координатами

Время обратить внимание на одну из ключевых особенностей интегральных изображений, которая до сих пор ограничивает область их применения, а именно ― ресурсоемкость и численную устойчивость. Так, в зависимости от диапазона величин, которые содержит оригинальное изображение, для его интегрального изображения может потребоваться более «длинный» тип данных. К примеру, при расчете среднеквадратичных отклонений кроме оригинального изображения (диапазон значений 0..255) используется изображение, содержащее квадраты соответствующих величин (диапазон значений 0..65535). В этом случае для вычисления интегральных изображений большого размера 32 бит точности оказывается недостаточно^[20].

Похожая ситуация наблюдается и в случае интегральных изображений со взвешенными координатами. Сама по себе величина суммы координат, которую необходимо хранить в интегральном изображении, растет в зависимости от размера изображения N: квадратично для одномерного случая 0 + 1 + 2 +… + N ― 1 = (N ― 1)*N/2 и кубически для двумерного N*(N ― 1)*N/2. Например, чтобы хранить сумму одной целочисленной координаты для изображения размером 2048×2048 (равную 4292870144), едва хватит 32-битного беззнакового целого (максимальное значение которого 4294967295). При вычислении интегральных изображений большего размера наступит переполнение.

Использование в интегральных изображениях 32-битных чисел с плавающей точкой отдаляет проблему переполнения на астрономическое расстояние (10³⁸ ― 10¹⁰), но при этом точность вычислений со взвешенными координатами значительно снижается из-за накапливаемой при суммировании ошибки усечения^[21].


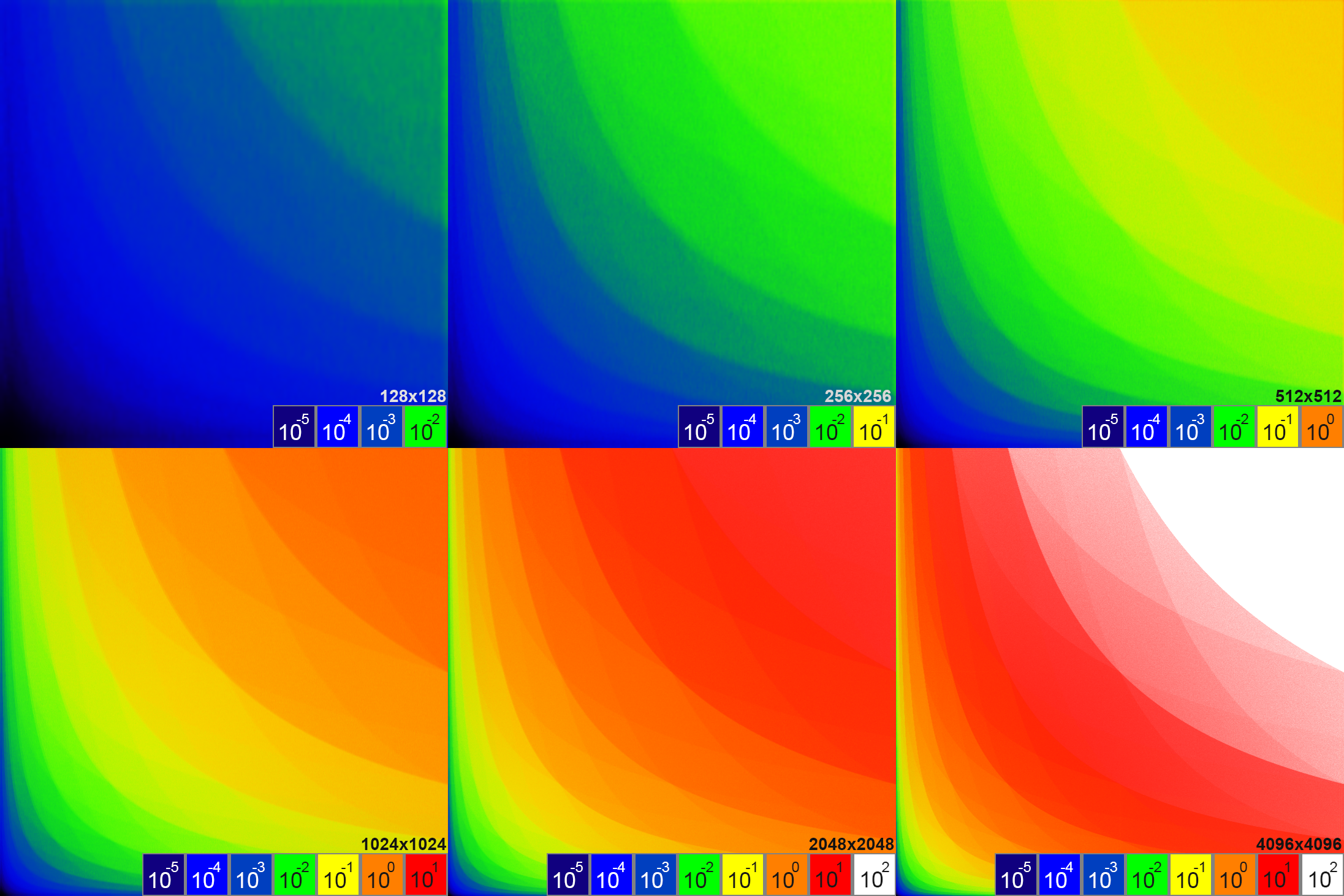
Абсолютная величина ошибки при вычислении взвешенного центра масс региона размером 4×4 элемента. Интегральное изображение содержит числа с одинарной точностью (32 бита).


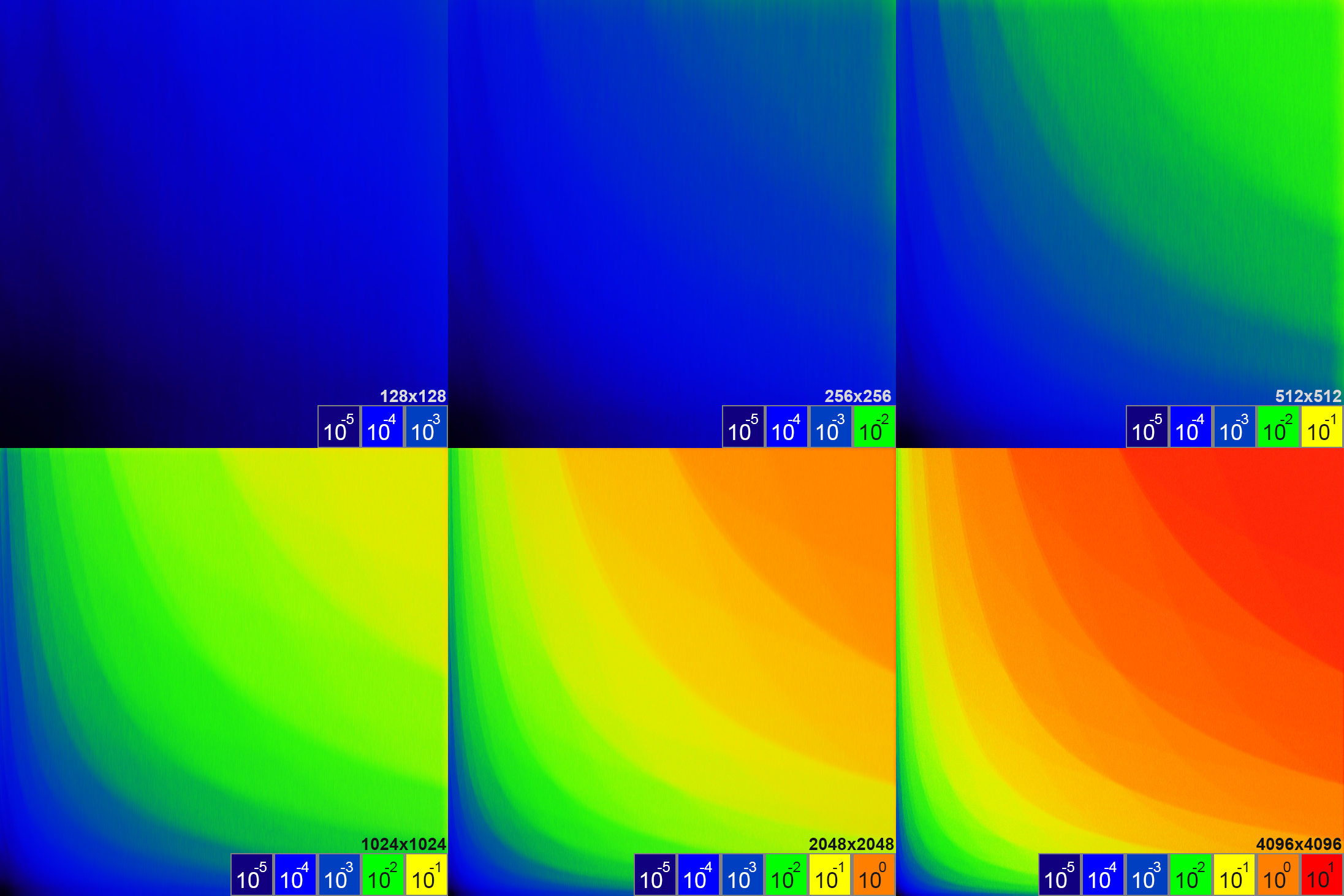
Абсолютная величина ошибки при вычислении взвешенного центра масс региона размером 32×32 элемента. Интегральное изображение содержит числа с одинарной точностью (32 бита).

Наибольшей абсолютной величины достигают ошибки вычисления взвешенного центра масс для небольших регионов. Увеличение размера региона на два порядка приводит к снижению величины абсолютной ошибки вычислений на четыре порядка. При этом не обнаружено зависимости погрешности вычислений от диапазона значений весовых коэффициентов (которые используются для вычислений взвешенных координат элементов).


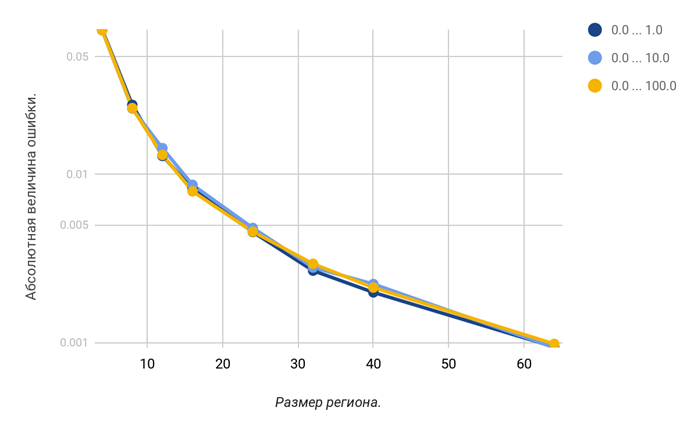
Увеличение диапазона значений весовых коэффициентов не влияет на абсолютную величину ошибки при расчете взвешенного центра масс. На графике приведены погрешности для «худшего» региона (в верхнем правом углу интегрального изображения). Размер интегрального изображения ― 256×256 элементов.


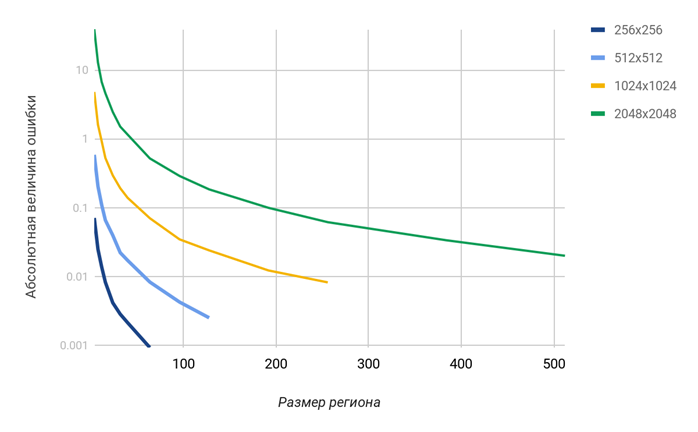
Абсолютная величина ошибки при расчете взвешенного центра масс уменьшается при увеличении размера региона. На графике приведены погрешности для «худшего» региона (в верхнем правом углу интегрального изображения).

Исходя из описанного выше анализа можно сделать вывод, что использование чисел с одинарной точностью для вычисления взвешенных центров масс с помощью интегральных изображений имеет практический смысл лишь для изображений размером около 512×512 элементов. При дальнейшем увеличении размеров величина погрешности становится сопоставимой с размерами элемента изображения. И хотя эта погрешность снижается с увеличением размера региона, наибольшее влияние на конечный результат ― величину силы гравитации ― оказывают именно регионы небольшого размера, поэтому и принимать в расчет нужно только соответствующие им погрешности.

Что касается изображений большего размера ― для них можно использовать взвешенные координаты двойной точности либо добавить еще один уровень дискретизации: разбить оригинальное изображение на несколько частей и считать интегральные изображения отдельно для каждой из этих частей. С точки зрения вычислительной сложности, если для вычисления суммы элементов региона используется более чем одно интегральное изображение, но это «более чем одно» является константой, сложность алгоритма подсчета суммы не меняется.

Заключение

Приведенный выше пример использования интегрального изображения, вероятно, можно адаптировать для разработки оптимального алгоритма O(1) выборки по значимости (importance sampling). Существующие ― и крайне ресурсоемкие с точки зрения GPU ― алгоритмы имеют линейную сложность O(N) и находят применение в современных методах глобального освещения^{[22, 23]}.

В целом, на мой взгляд, интегральные изображения ― один из самых недооцененных алгоритмов. Они могут составить великолепную альтернативу одновременно мипмаппингу и анизотропной фильтрации, а с учетом того, как именно реализовано последнее на GPU^{[24, 25]}, вполне возможно, что являются уже и более эффективной мерой.

Ссылки