
Полгода назад мне захотелось создать лучший генератор псевдослучайных чисел (ГПСЧ) с какой-нибудь необычной архитектурой. Я думал, что начало будет лёгким, а по мере работы задача станет медленно усложняться. И думал, смогу ли я научиться всему достаточно быстро, чтобы справиться с самым сложным.
К моему удивлению, сложность возрастала не линейно. Побайтовое тестирование по критерию хи-квадрат оказалось очень трудным! Позднее столь же трудно было пройти тесты diehard. Я опубликовал текущие результаты, чтобы понять, какие ещё трудности меня ожидают. Однако тест PractRand в тот раз пройти не удалось.
Затем было очень трудно прохождение теста BigCrush.
Затем было очень трудно передавать 32 тебибайта данных при прохождении PractRand. Скорость стала проблемой. Мало было создать конструкцию, генерирующей десять мегабайтов в секунду, потому что прохождение PractRand заняло бы месяц. Но должен признаться, что пройти этот тест со скоростью гигабайт в секунду было очень трудно.
Когда поднимаешься на такую высоту… тебе хочется узнать, сможешь ли ты добраться до границы Парето. Ты хочешь создать самый быстрый в мире ГПСЧ, который пройдёт самые сложные статистические тесты.
Мне это удалось.
В предыдущей статье я рассказал, чему научился, чтобы добиться своей цели. А здесь я расскажу, как работает финальная архитектура.
Цель
Начнём с очевидного: скорость зависит от платформы. Я сосредоточился на оптимизации под современную архитектуру x86-64 (процессоры Intel и AMD).
Для сравнения производительности используется классическая метрика cpb: это количество циклов процессора, потраченных на генерирование одного байта. Эта метрика вычисляется и сравнивается во всех криптографических работах. Чуть меньшая величина cpb в мире ПО или оборудования может обеспечить победу в соревновании или использование на веб-сайтах по всему миру.
Чтобы улучшить cpb, можно:
- Генерировать больше байтов при том же объёме работы,
- Или делать меньше работы, чтобы генерировать тоже количество байтов,
- Или распараллелить работу.
Мы сделаем всё перечисленное.
Согласно первому пункту, нам нужно при каждой итерации выдавать больше битов.
Я боялся, что мне будут говорить: «Если он не выдаёт 32-битные числа, то это не ГПСЧ», или то же самое с 64-битными числами. Или: «ГПСЧ должен быть предназначен только для архитектуры x86-64», словно запрещены инструкции вроде POPCNT или регистры вроде %xmm7.
Однако ГПСЧ — это инженерия: авторы генераторов уже несколько десятилетий стараются выжать из процессоров всё возможное! Когда появился ROL, они начали полагаться на него. С появлением 64-битных процессоров стали полагаться на %rax. Конечно, на ARM такие алгоритмы могут работать медленнее (хотя это ещё предстоит выяснить), однако 64-битные ГПСЧ активно использовались ещё до того, как Android начал требовать в 2019-м поддержку 64-битности!
То есть эта сфера развивается вместе с аппаратной частью. И сегодня процессоры Intel и AMD за счёт AVX2 поддерживают уже 256-битные операции. RC4 выдавал 1 байт, drand48 мог за раз выдавать 4 байта, pcg64 — 8 байтов, а теперь мы можем сразу генерировать по 32 байта.
8 байтов могут представлять собой 64-битное число, и в большинстве языков программирования есть для этого встроенные типы. Но мало какие языки предоставляют типы для 16 байтов (примечательное исключение — __uint128_t в С). Ещё меньше языков имеют тип для 32 байтов (кроме внутренних).
Так что можем попрощаться с обычным прототипом ГПСЧ-функции (пример из бенчмарка Виньи HWD):
static uint64_t next(void);
Вместо этого можно сделать генератор, заполняющий буфер (пример из моего бенчмарка):
void prng_gen(prng_state *s, __uint64_t buf[], __uint64_t size);
Какие у этого решения недостатки?
Если ваш генератор выдаёт по 32 байта за раз, то нужно, чтобы потребитель предоставил массив, кратный 32 (в идеале, выровненный по 32 байтам). Хотя можно обойтись и без этого, просто будем заполнять буфер. Неиспользованные данные будем из него убирать и снова заполнять по мере необходимости. Задержка становится непредсказуемой: некоторые вызовы будут просто читать буфер. Но в среднем всё будет так же.
Теперь мы генерируем больше байтов, делая тот же объём работы. Как нам распараллелить её?
Параллелизм
Процессоры предлагают на всех уровнях невероятный набор инструментов распараллеливания.
Во-первых, это SIMD-инструкции (Single-Instruction, Multiple Data). Например, AVX2 параллельно выполняет четыре 64-битных сложения, или восемь 32-битных, и т.д.
В криптографии это используют уже лет пятнадцать. Параллелизм обеспечил невероятную производительность ChaCha20. Его применяют большинство важных примитивов, не использующих AESNI. Например, NORX и Gimli спроектированы с учётом параллелизма.
Недавно в некриптографическом ГПСЧ-сообществе тоже возрос интерес к этой теме. В частности, существующие примитивы, которые проектировались не под SIMD, могут стать основой для создания очень быстрых ГПСЧ.
Когда Себастьяно Винья (Sebastiano Vigna) продвигал свою архитектуру xoshiro256++ в стандартной библиотеке языка Julia, он выяснил, что результаты восьми конкурентных, по-разному инициализированных экземпляров ГПСЧ можно конкатенировать очень быстро, если каждую операцию исполнять одновременно во всех ГПСЧ.
SIMD — лишь один из уровней распараллеливания в процессоре. Рекомендую прочитать предыдущую статью по этой теме, чтобы иметь лучшее представление, но я буду давать некоторые пояснения.
Конвейеры процессора позволяют обрабатывать на разных стадиях по несколько инструкций. Если хорошо организовать порядок их исполнения, чтобы уменьшить зависимости между стадиями, то можно ускорить обработку инструкций.
Суперскалярное исполнение позволяет одновременно обрабатывать вычислительные части инструкций. Но для этого они не должны иметь зависимостей на чтение-запись. Можно адаптировать архитектуру для снижения риска простоев, выполняя запись задолго до чтения.
Внеочередное исполнение позволяет процессору исполнять инструкции не в порядке следования, а по мере их готовности, даже если предыдущие инструкции ещё не готовы. Но для этого не должно быть зависимости на чтение-запись.
А теперь переходим к реализации!
Архитектура
Рассмотрим схему, которая называется полу-SHISHUA. Откуда такое название, станет постепенно очевидно по мере чтения.
Схема выглядит так:

Рассмотрим её строка за строкой.
typedef struct prng_state {
__m256i state[2];
__m256i output;
__m256i counter;
} prng_state;
Состояние делится на две части, которые помещаются в регистр AVX2 (256 бит). Для повышения скорости мы держим результат недалеко от самого состояния, но он не является частью состояния.
Также у нас есть 64-битный счётчик. Для упрощения вычисления он тоже является регистром AVX2. Дело в том, что у AVX2 есть небольшая особенность: обычные регистры (%rax и подобные) не могут посредством MOV передаваться напрямую в SIMD, они должны проходить через оперативную память (чаще всего через стек), что повышает задержку и обходится в две процессорные инструкции (MOV в стек, VMOV из стека).
Теперь посмотрим на генерирование. Начнём с загрузки, затем пройдёмся по буферу и на каждой итерации заполним его 32 байтами.
inline void prng_gen(prng_state *s, __uint64_t buf[], __uint64_t size) {
__m256i s0 = s->state[0], counter = s->counter,
s1 = s->state[1], o = s->output;
for (__uint64_t i = 0; i < size; i += 4) {
_mm256_storeu_si256((__m256i*)&buf[i], o);
// …
}
s->state[0] = s0; s->counter = counter;
s->state[1] = s1; s->output = o;
}
Поскольку функция заинлайнена, немедленное заполнение буфера при старте позволяет процессору сразу же исполнять зависящие от этого инструкции посредством механизма внеочередного исполнения.
Внутри цикла мы быстро выполняем три операции над состоянием:
- SHIft
- SHUffle
- Add
Отсюда название SHISHUA!
Сначала выполняем сдвиг (shift)
u0 = _mm256_srli_epi64(s0, 1); u1 = _mm256_srli_epi64(s1, 3);
К сожалению, AVX2 не поддерживает обороты. Но я хочу перемешать биты одной позиции в 64-битном числе с битами другой позиции! И сдвиг — лучший способ это реализовать. Будем сдвигать на нечётное число, чтобы каждый бит побывал на всех 64-битных позициях, а не на половине из них.
При сдвиге теряются биты, что приводит к удалению информации из нашего состояния. Это плохо, нужно минимизировать потери. Самые маленькие нечётные числа — 1 и 3, мы будем использовать разные значения сдвига, чтобы увеличить расхождение между двумя частями. Это поможет уменьшить сходство их самокорреляции.
Будем сдвигать вправо, потому что крайние правые биты имеют самое низкое диффузия при сложении: например, младший бит в A+B — это просто XOR младших битов A и B.
Перемешивание
t0 = _mm256_permutevar8x32_epi32(s0, shu0); t1 = _mm256_permutevar8x32_epi32(s1, shu1);
Воспользуемся 32-битным перемешиванием, потому что оно даёт иную гранулярность по сравнению с 64-битными операциями, которые мы везде используем (нарушается 64-битное выравнивание). К тому же это может быть cross-lane операция: другие перемешивания могут двигать биты в рамках левых 128 битов, если они операции начинаются слева, или в рамках правых 128 битов, если начинаются справа.
Константы перемешивания:
__m256i shu0 = _mm256_set_epi32(4, 3, 2, 1, 0, 7, 6, 5),
shu1 = _mm256_set_epi32(2, 1, 0, 7, 6, 5, 4, 3);
Чтобы перемешивание действительно улучшило результат, мы передвинем слабые (с низким рассеиванием) 32-битные части 64-битных сложений на сильные позиции, чтобы следующие сложения их обогащали.
Младшая 32-битная часть 64-битного чанка никогда не перемещается в тот же 64-битный чанк, что и старшая часть. Таким образом, обе части не остаются в рамках одного чанка, что улучшает перемешивание.
В конце концов каждая 32-битная часть проходит по всем позициям по кругу: с A на B, с B на C, … с H на A.
Вы могли заметить, что простейшее перемешивание, учитывающее все эти требование, представляет собой два 256-битных оборота (обороты на 96 битов и 160 битов вправо соответственно).
Сложение
Сложим 64-битные чанки из двух временных переменных — сдвига и перемешивания.
s0 = _mm256_add_epi64(t0, u0); s1 = _mm256_add_epi64(t1, u1);
Сложение — это главный источник рассеивания: при этой операции биты комбинируют в несокращаемые комбинации выражений XOR и AND, распределённые по 64-битным позициям.
Хранение результата сложения внутри состояния навсегда сохраняет это рассеивание.
Выходная функция
Откуда мы получаем выходные данные?
Всё просто: созданная нами структура позволяет генерировать две независимые части состояния s0 и s1, которые никак не влияют друг на друга. Применяем к ним XOR и получаем совершенно случайный результат.
Для усиления независимости между данными, к которым мы применяем XOR, возьмём частичный результат: сдвинутую часть одного состояния и перемешанную часть другого.
o = _mm256_xor_si256(u0, t1);
Это аналогично уменьшению зависимостей по чтению-записи между инструкциями в суперскалярном процессоре, как если бы u0 и t1 были готовы для чтения до s0 и s1.
Теперь обсудим счётчик. Мы обрабатываем его в начале цикла. Сначала изменяем состояние, а затем увеличиваем значение счётчика:
s1 = _mm256_add_epi64(s1, counter);
counter = _mm256_add_epi64(counter, increment);
Почему сначала меняем состояние, а потом обновляем счётчик? s1 становится доступен раньше, это снижает вероятность того, что последующие инструкции, которые его читают, остановятся в конвейере процессора. Также эта очерёдность помогает избежать прямой зависимости счётчика по чтению-записи.
Мы применяем счётчик к s1, а не к s0, потому что они всё-равно оба влияют на выходные данные, однако, s1 теряет из-за сдвига больше битов, так что это помогает ему «встать на ноги» после сдвига.
Счётчик может и не зафиксировать прохождение теста PractRand. Его единственная цель — задать нижнюю границу в 269 байтов = 512 эксбибайтов на период ГПСЧ: мы начинаем повторять цикл только через одно тысячелетие работы со скоростью 10 гибибайтов в сек. Вряд ли это будет слишком низкой скоростью для практического применения в ближайшие века.
Инкрементирование:
__m256i increment = _mm256_set_epi64x(1, 3, 5, 7);
В качестве инкрементов выбираются нечётные числа, потому что только базовые взаимно простые числа охватывают весь цикл конечного поля GF(264), а все нечётные числа являются взаимно простыми для 2. Иными словами, если вы инкрементируете по чётному целому числу в диапазоне от 0 до 4, возвращаясь к 0 после 4, то получается последовательность 0-2-0-2-…, которая никогда не приведёт к 1 или 3. А нечётный инкремент проходит через все целые числа.
Для всех 64-битных чисел в состоянии мы применим разные нечётные числа, что ещё больше разделит их и немного усилит смешивание. Я выбрал самые маленькие нечётные числа, чтобы они не выглядели волшебными.
Так работает переход между состояниями и выходная функция. Как их инициализировать?
Инициализация
Инициализируем состояние с помощью шестнадцатеричных цифр ? — иррационального числа, которое меньше всего аппроксимируется дробью.
static __uint64_t phi[8] = {
0x9E3779B97F4A7C15, 0xF39CC0605CEDC834, 0x1082276BF3A27251, 0xF86C6A11D0C18E95,
0x2767F0B153D27B7F, 0x0347045B5BF1827F, 0x01886F0928403002, 0xC1D64BA40F335E36,
};
Возьмём 256-битное начальное число. Так часто делается в криптографии и не вредит работе некриптографических ГПСЧ:
prng_state prng_init(SEEDTYPE seed[4]) {
prng_state s;
// …
return s;
}
Мы не хотим с помощью этого начального числа переопределять всю часть состояния (s0 или s1), нам нужно повлиять лишь на половину. Так мы избежим использования ослабляющих начальных чисел, которые случайно или намеренно задают известное слабое начальное состояние.
Поскольку мы не меняем половину каждого состояния, мы сохраняем контроль над 128 битами состояния. Такой энтропии достаточно для начала и сохранения сильной позиции.
s.state[0] = _mm256_set_epi64x(phi[3], phi[2] ^ seed[1], phi[1], phi[0] ^ seed[0]);
s.state[1] = _mm256_set_epi64x(phi[7], phi[6] ^ seed[3], phi[5], phi[4] ^ seed[2]);
Затем мы несколько раз повторяем (
ROUNDS) такую последовательность:- Прогоняем этапы (
STEPS) итераций SHISHUA. - Присваиваем одну часть состояния другому состоянию, а другую часть — выходному результату.
for (char i = 0; i < ROUNDS; i++) {
prng_gen(&s, buf, 4 * STEPS);
s.state[0] = s.state[1];
s.state[1] = s.output;
}
Присвоение выходному результату повышает рассеивание состояния. При инициализации не имеет значения дополнительная работа и корреляция состояний, потому что эта серия операций выполняется однократно. Нас интересует только рассеивание при инициализации.
Оценив влияние на корреляцию начальных значений, я выбрал для
STEPS значение 2, а для ROUNDS — 10. Корреляцию я вычислил, подсчитав «необычные» и «подозрительные» аномалии, возникающие из-за инструментария проверки качества ГПСЧ в PractRand.Производительность
Измерять скорость сложно по нескольким причинам:
- Измерение по часам может иметь недостаточную точность.
- В процессоре столько всего распараллеливается, что отслеживание начала и конца инструкций, во-первых не детерминировано, а во-вторых, сильно зависит от других событий в процессоре.
- Очевидно, что на процессорах разных производителей результаты будут разными. То же самое относится и к разным сериям процессоров одного производителя.
- Сегодня процессоры имеют переменную тактовую частоту: работают быстрее или медленнее в зависимости от нагрузки, чтобы снизить потребление энергии или риск перегрева.
Я использую процессорную инструкцию RDTSC, которая вычисляет количество циклов.
Чтобы любой желающий мог воспроизвести мои результаты, я использую облачную виртуальную машину. Это не меняет уровень результатов бенчмарка по сравнению с локальным тестированием. Кроме того, вам не придётся покупать такой же компьютер, как у меня. И наконец, есть много ситуаций, когда ГПСЧ запускают в облаках.
Я выбрал Google Cloud Platform N2 (процессор Intel) и N2D (процессор AMD). Достоинство GCP в том, что они предлагают серверы с процессорами обоих производителей. В статье мы сосредоточимся на Intel, но для AMD результаты будут того же порядка.
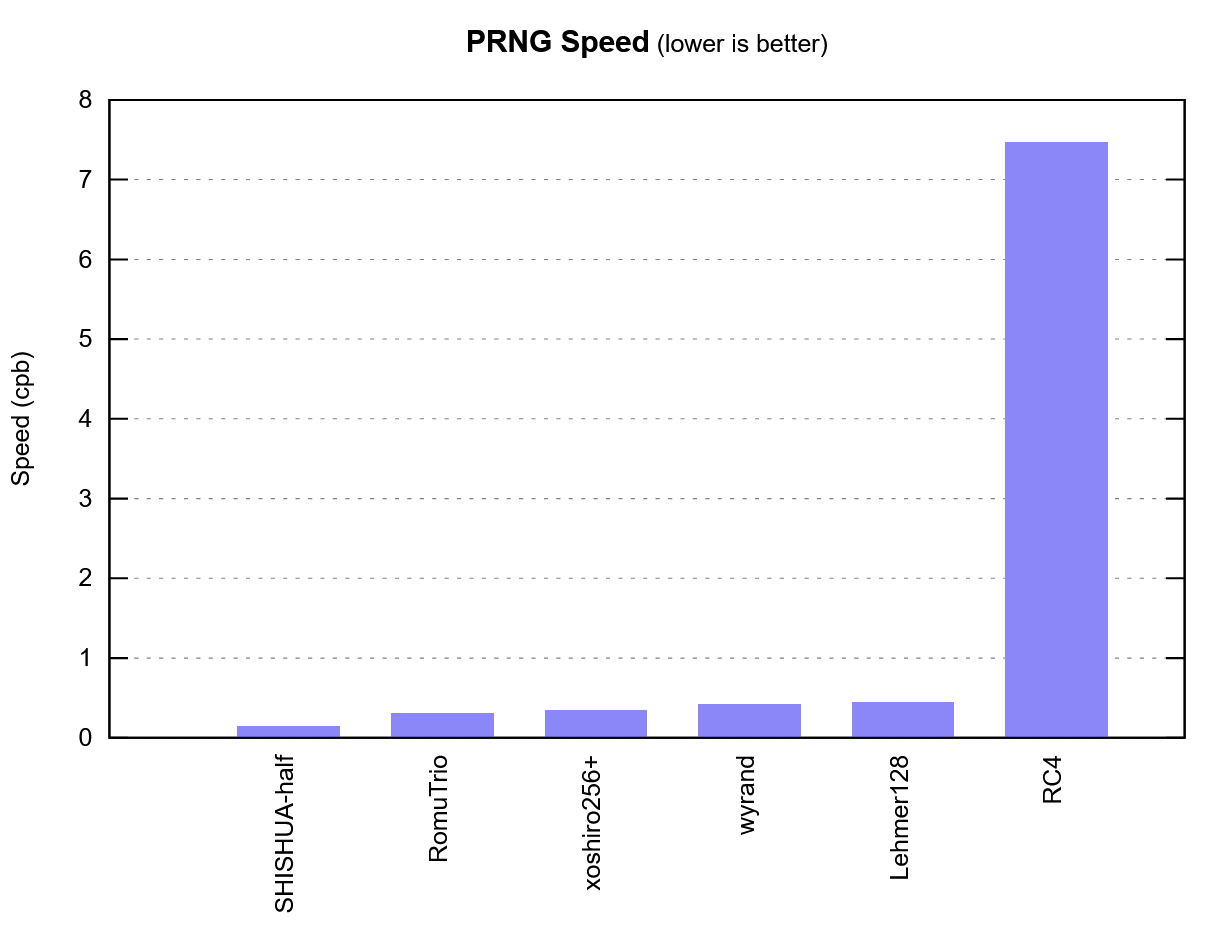
Чтобы глубже погрузиться в тему, давайте сначала прогоним старый криптографический генератор RC4. Не имея возможности распараллелить работу, я получил 7,5 cpb (циклов на сгенерированный байт).
Теперь прогоним очень популярный и быстрый MCG: простейший ГПСЧ Lehmer128, который проходит тест BigCrush, показал 0,5 cpb. Ого, отлично!
Затем прогоним свежую разработку, которая используется для быстрых хэш-таблиц — wyrand. 0,41 cpb, чуть лучше!
Некоторые ГПСЧ не проходят 32-тебибайтный тест PractRand, но работают очень быстро. Xoshiro256+ дотянул только до 512 мебибайтов, но продемонстрировал очень высокую скорость: 0,34 cpb.
Ещё одна свежая разработка RomuTrio. Она претендует на титул самого быстрого ГПСЧ в мире — 0,31 cpb.
Ладно, этого хватит. Что показал полу-SHISHUA?
0,14 cpb. Вдвое быстрее RomuTrio.
Круто. Теперь протестируем криптографический генератор ChaCha8. Он достиг… 0,12 cpb.
Ой.
SIMD — это настоящее волшебство!
Для криптографического сообщества это не стало особым сюрпризом. ChaCha8 необычайно легко распараллеливать. Это лишь хорошо хэшированный счётчик в рассеянном состоянии.
А ещё помните, как команда языка Julia пыталась объединить несколько экземпляров архитектуры Виньи, чтобы создать быстрый ГПСЧ на основе SIMD? Давайте посмотрим на их результат, воспользовавшись этой методикой (8 штук Xoshiro256+). 0,09 cpb!
Технически, мой ноутбук мог повлиять на результаты. Я не уверен, почему разработка команды Julia работает быстрее ChaCha8 в GCP, но медленнее при локальном тестировании. На моей машине полу-SHISHUA работает быстрее разработки команды Julia, но медленнее ChaCha8.
Нужно победить всех конкурентов.
Вероятно, вы уже спрашиваете, почему мы назвали предыдущую версию генератора полу-SHISHUA? Потому что оказалось легко повысить скорость вдвое, если запустить два экземпляра полу-SHISHUA.
Аналогично идее команды Julia, инициализируем отдельно два ГПСЧ (четыре блока 256-битного состояния), поочерёдно подавая на выход результаты их работы.
Но если сделать больше состояний, то мы можем выдавать ещё больше данных, попарно комбинируя четыре состояния:
o0 = _mm256_xor_si256(u0, t1);
o1 = _mm256_xor_si256(u2, t3);
o2 = _mm256_xor_si256(s0, s3);
o3 = _mm256_xor_si256(s2, s1);
Так мы получили SHISHUA, который показал скорость в 0,06 cpb.
Это вдвое быстрее предыдущего самого быстрого конкурента в мире, который прошёл 32-тебибайтный тест PractRand. Результат на графике.
Полагаю, разработка получилась конкурентоспособной. На моём ноутбуке работает ещё быстрее — 0,03 cpb, но буду придерживаться своих принципов касательно бенчмарка.
Надеюсь, ещё несколько недель мой генератор продержится на пьедестале самого быстрого в мире (пожалуйста, сделайте так).
Качество
Генератор честно проходит BigCrush и 32-тебибайтный тест PractRand. И всё благодаря четырём выходным потокам.
К недостаткам архитектуры можно отнести её необратимость. Это видно по уменьшению до 4-битного состояния с
s0 = [a, b] и s1 = [c, d]. При сдвиге мы получаем [0, a] и[0, d], а при перемешивании — [b, c] и [d, a]. Новый s0 равен [b, c] + [0, a] = [b?(a?c), a?c], а s1 равен [d, a] + [0, c] = [d?(a?c), a?c]. Если a = ¬c, тогда a?c = 1 и a?c = 0, следовательно, s0 = [b, 1] и s1 = [d, 1]. То есть получаем две комбинации a and c, которые дают нам то же финальное состояние.В нашем случае это не является проблемой, потому что 64-битный счётчик тоже является частью состояния. Получается минимальный цикл в 271 байта (по 128 байтов на переход между состояниями), который на скорости в 10 гибибайтов/сек. продлится семь тысяч лет. Это уравновешивает потерянные состояния.
Кроме того, даже несмотря на необратимость средний период перехода между состояниями равен 2^((256+1)?2). Это даёт средний цикл в 2135 байтов (на скорости в 10 гибибайтов/сек. будет длиться более чем в триллион раз дольше, чем существует Вселенная). Хотя я считаю, что средние циклы переоценивают, потому что они ничего нам не говорят о качестве работы генератора.
Вот результаты бенчмарка:
| Генератор | Производительность | Качество | Корреляция начальных чисел |
|---|---|---|---|
| SHISHUA | 0,06 | >32 ТиБ | >256 ГиБ |
| xoshiro256+x8 | 0,09 | 1 КиБ | 0 КиБ |
| ChaCha8 | 0,12 | >32 ТиБ? | >32 ТиБ? |
| RomuTrio | 0,31 | >32 ТиБ | 1 КиБ |
| xoshiro256+ | 0,34 | 512 МиБ | 1 КиБ |
| wyrand | 0,41 | >32 ТиБ | 8 КиБ |
| Lehmer128 | 0,44 | >32 ТиБ | 1 КиБ |
| RC4 | 7,48 | 1 ТиБ | 1 КиБ |
- Производительность: количество циклов процессора, потраченных на один сгенерированный байт. Получено на облачных машинах N2 GCP и N2D (AMD), порядок одинаковый.
- Качество: уровень, на котором генератор заваливает прохождение теста PractRand. Если не заваливает, стоит знак >. Если результат не доказан, стоит вопросительный знак.
- Корреляция начальных чисел: прохождение PractRand с чередованием байтов из восьми потоков с начальными числами 0, 1, 2, 4, 8, 16, 32, 64. Мы используем PractRand со свёрткой вдвое и расширенными тестами.

Далее
Хотя в нашем случае нет никаких проблем с необратимостью, всё же мы можем улучшить SHISHUA.
В моём представлении идеальный ГПСЧ обладает такими свойствами:
- Переход между состояниями представляет собой циклическое преобразование, что даёт цикл в 21024. Для его завершения со скоростью 10 гибибайт/сек. понадобится времени в 10282 раз больше, чем возраст Вселенной. Это не совсем «лучше» (невозможность есть невозможность). Но если мы можем уменьшить архитектуру до более мелкого состояния без влияния на рассеивание, то можем получить ещё более быстрый ГПСЧ. Как думаете, удастся ли уместить его в 128-битный регистр NEON в процессорах ARM? Кроме того, нам больше не нужен будет счётчик, что сэкономит две операции сложения.
- Выходная функция является доказанно необратимой. Это нами уже достигнуто благодаря тому, как в SHISHUA применяется XOR к двум независимым числам. Но я ещё не доказал, что числа действительно не коррелируют.
- Инициализация состояния необратима, когда у каждого состояния есть 2128 возможных начальных чисел (чтобы предотвратить возможность угадать начальное число). Способ присвоения состояния своему собственном результату в SHISHUA, скорее всего, обеспечивает необратимость. Кроме того, мы используем переход между состояниями (частично необратим) и выходную функцию (вероятно, необратима, см. пункт 2).
- У инициализации состояния идеальное рассеивание: все биты начального числа влияют на все биты состояния с одинаковой вероятностью. Хочу это выяснить применительно к SHISHUA.
Одной из проблем, сдерживающих развитие ГПСЧ и криптографии в целом, является отсутствие более качественного инструментария общего назначения. Мне нужен инструмент, который может сразу выдать мне точный результат измерений, чтобы я мог на лету сравнивать разные архитектуры.
PractRand великолепен по сравнению с тем, что было до него, однако:
- Он не позволяет оценивать высококачественные генераторы, делая невозможным их сравнение друг с другом. Нам приходится говорить: «ну, после 32 тебибайтов у них нет никаких аномалий...»
- На его прогон уходят недели...
Надеюсь, скоро ситуация сильно улучшится.


Scratch
Ну вот, наконец-то годнота! А то уже докатились до имитовставок.
Вам эта штука, если не секрет, для чего?