29.04.2020 11:58
kriot 2 6800 Источник

Хочу с вами зачелленджить одну интересную штуку: попробовать обучить нейросеть в Google Таблицах. Безо всяких макросов и прочих хаков, на чистых формулах.



Дисклеймер: Это просто пример к "в экселе можно сделать все". Для машинного обучения есть много других более подходящих инструментов.


Задачка нетривиальная, поэтому начнем с более простого случая: склепаем итеративное обучение линейной регрессии. Это частный случай нейросети: однослойная сетка с линейной активацией. Поэтому мы сможем взять этот пример в качестве базового.


Учим линейную регрессию


Заведем табличку, закинем рандомные данные. Таргет сгенерируем линейно, возьмем коэффициенты 1 и 2, чтобы было очевидно, к чему должна приблизиться модель.



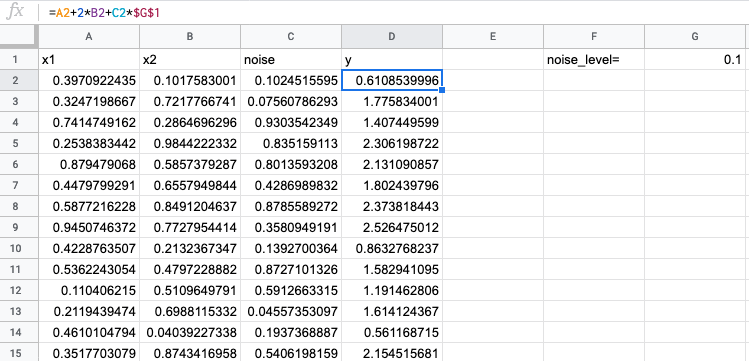
Добавим несмещенный шум (с нулевым матожиданием) и сделаем настройку по его уровню, чтобы подкрутить, если что.


Заводим новую страницу, на ней будем учить модель. В каждой строчке будет новая итерация. Первые два столбца — веса модели, а дальше будут идти столбцы с вычисляемыми параметрами. Вычислять будем градиент по весам и MSE. На каждой следующей строчке будем прибавлять к весам обновления с прошлой итерации и, таким образом, получать более точную модель.


Посчитаем MSE — по нему будем определять, что от итерации к итерации модель улучшается. Ошибку будем считать на обучающей выборке. Конечно, мы можем переобучить модель, но наша цель — не модель хорошую построить, а научиться ее оптимизировать под данные. MSE по обучающей выборке как раз будет показывать, насколько удачно мы подогнали модель именно под эти данные.



Формула: SUM(ARRAYFORMULA(POW(Data!$A$2:$A*$A4 + Data!$B$2:$B*$B4 - Data!$D$2:$D, 2)))/COUNT(Data!$A$2:$A)


Пояснение: POW(Data!$A$2:$A*$A4 + Data!$B$2:$B*$B4 - Data!$D$2:$D, 2) вычисляет ошибку для одного примера. Благодаря команде ARRAYFORMULA вычисление применятся ко всему списку примеров. Суммируем и делим на количество, чтобы усреднить. Не используем AVERAGE, потому что ARRAYFORMULA в этой конструкции отдает массив с кучей нулей в хвосте.


Потом вычисляем градиент по весам. Про градиентный спуск написано миллион статей; например, тут считают градиент, который мы используем. Формула градиента для нашего случая: $(x_1*w_1 + x_2*w_2 - y)*x_i$, где $i$ — это номер веса, для которого мы считаем градиент.



Формула: SUM(ARRAYFORMULA((Data!$A$2:$A*$A4 + Data!$B$2:$B*$B4 - Data!$D$2:$D)*Data!$A$2:$A))/COUNT(Data!$A$2:$A) — поэлементно вычисляем градиент, потом усредняем.


Теперь обновляем веса. Двигаемся против градиента пропорционально шагу обучения. Таким образом мы получили новые, более хорошие веса.



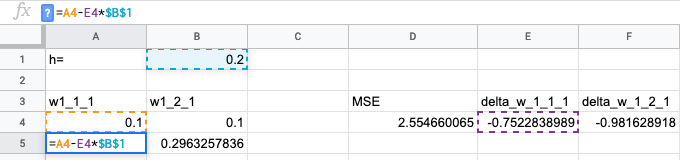
Протягиваем формулы вниз:



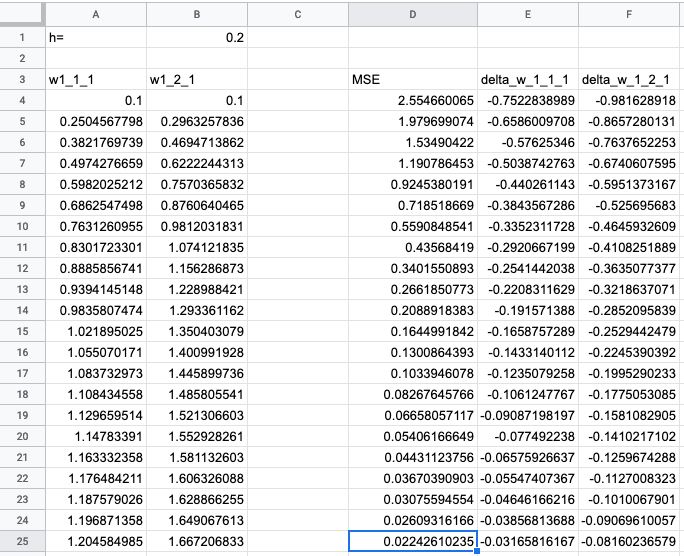
Ошибка уменьшается, значит, модель оптимизируется. Веса меняются монотонно — это говорит о том, что модель еще не доучилась. Подкрутим скорость обучения, поставим h = 2:



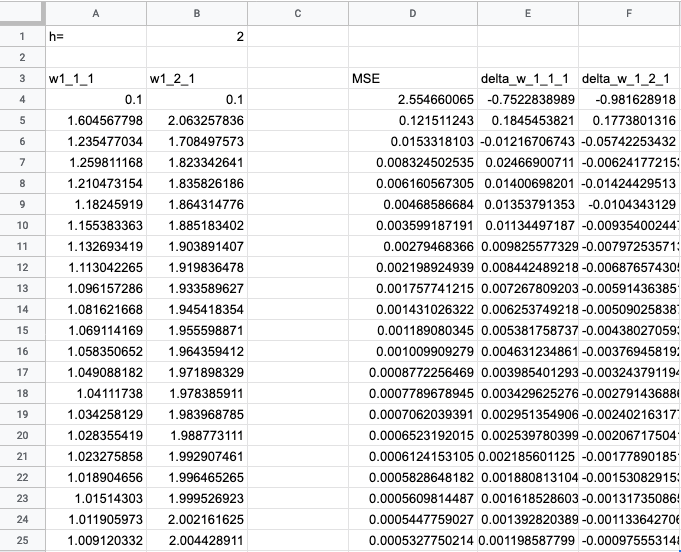
Ошибка стала совсем маленькой, а веса близки к тем, которые мы ожидали. Успех!


Обучаем нейросеть


Сделаем новый таргет y2, чтобы он был не таким линейным, как y:



График этой формулы выглядит так (у нас область данных меньше, чем на графике):



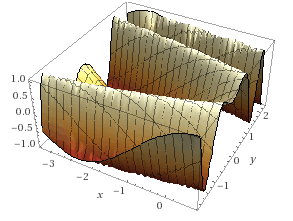
Будем использовать нейросеть с промежуточным полносвязным слоем из двух нейронов. Во внутреннем слое функция активации — сигмоида, во внешнем — линейная. Для простоты модель будем делать без сдвига.
Параметры модели:


  • w1 — матрица перехода к внутреннему слою. Коэффициенты w1_1_1, w1_1_2, w1_2_1 и w1_2_2
  • w2 — матрица перехода к внешнему слою. Коэффициенты w2_1 и w2_2

Формулы берем отсюда и слегка модифицируем под наши обозначения:


  • $x$ — фичи, каждый пример на отдельной строке
  • $y_t$ — столбец таргета
  • $L = \sigma(W_1x^T) = \frac{1}{1-e^{W_1x^T}}$ — значения промежуточного слоя, экспонента применена поэлементно
  • $y = W_2L$ — вектор-строка результата сети
  • $\delta_{out} = y - y_t^T$ — вектор-строка ошибок
  • $\Delta W_2 = \delta_{out} L^T$ — градиент
  • $\delta_1 = W_2^T \delta_{out} \odot \sigma'(W_1x^T)$, где $\odot$ — поэлементное перемножение матриц. Это матрица ошибок на промежуточном слое
  • $\Delta W_1 = \delta_1 x$ — градиент

Выражаем градиенты через исходные данные:


  • $\Delta W_2 = (W_2\frac{1}{1-e^{W_1x^T}} - y_t^T) \frac{1}{1-e^{W_1x^T}}^T$
  • $\Delta W_1 = (W_2^T (W_2\frac{1}{1-e^{W_1x^T}} - y_t^T) \odot \frac{1}{1-e^{W_1x^T}} \odot (1-\frac{1}{1-e^{W_1x^T}})) x$

Для нас важно, чтобы не нужно было менять формулы при изменении количества примеров в выборке, поэтому все промежуточные вычисления должны укладываться в постоянное количество ячеек.


На самом деле, это не так

Можно сделать формулу, которая, в зависимости от своей позиции и количества примеров на входе, будет сама понимать какую функцию и от каких данных нужно вычислять. Потом эту формулу можно растиражировать на всю страницу и наслаждаться вычислениями с динамической структурой самих вычислений. Но это уже пахнет ультрахардкором.


Есть способ хранить любые векторы в одной ячейке. Сохранить список в ячейку можно, если сделать его строкой. Функция JOIN(",",{1,2,3}) превратит список в строку "1,2,3", а SPLIT("1,2,3", ",") превратит обратно в список.


Но я не знаю способа хранить матрицы в одной ячейке. Хак для векторов не подходит для матриц, потому что не получается при помощи JOIN обработать матрицу любого размера. ARRAYFORMULA не помогает. Если вы знаете способ, как это сделать, поделитесь, буду благодарен.


Промежуточные переменные $\delta_1$ и $L$ — матрицы размера (2, n). Это значит, что записать в лоб формулы мы не можем — не получится сохранить эти матрицы в ячейку. Выходит, у нас есть два варианта реализации вычислений:


  1. Сразу вычислять градиент, не сохраняя промежуточные результаты. В этом случае некоторые вычисления будут дублироваться.
  2. Сохранять промежуточные результаты, но каждую из матриц $\delta_1$ и $L$ хранить в двух ячейках построчно: вектором длины n для первой строки и вектором для второй.

Каждый из этих способов требует существенных изменений формул при изменении структуры сети. Мне чуть больше нравится первый способ, но веской аргументации у меня нет.


Клепаем формулы! Просто переписываем формулы для полного вычисления градиента в функциях экселя:



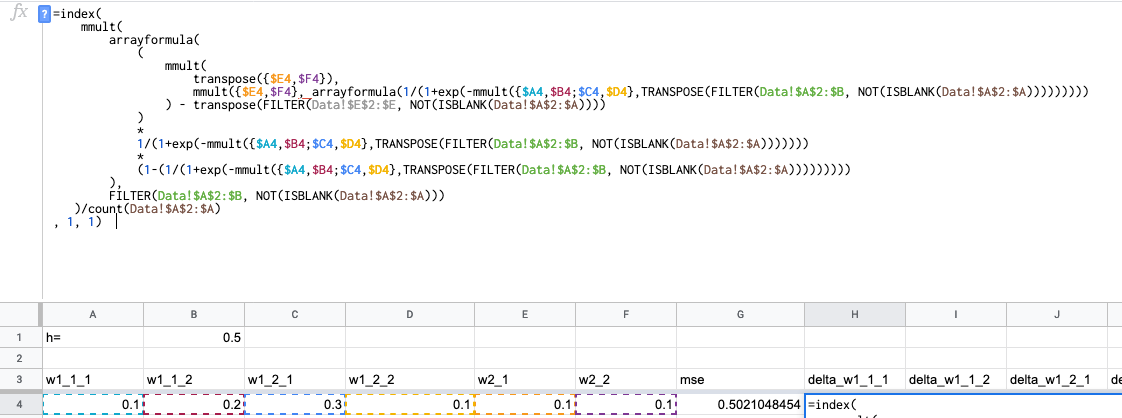
Несколько моментов:


  • Я фильтрую исходные данные: FILTER(Data!$A$2:$B, NOT(ISBLANK(Data!$A$2:$A))) — это нужно потому, что перемножение матриц работает только с конечными матрицами. Формула просто вырезает пустые строки из исходных данных.
  • Функцией INDEX я беру нужную компоненту градиента. Для формул delta_w1_1_2 индекс будет 1,2 и так далее.
  • Дополнительно делю на количество примеров: в исходных формулах функция ошибки не среднеквадратичное отклонение, а сумма квадратов отклонений. Делить нужно, чтобы нам не приходилось подкручивать скорость обучения при существенном изменении количества примеров.

Формула для w2_1, всё аналогично:



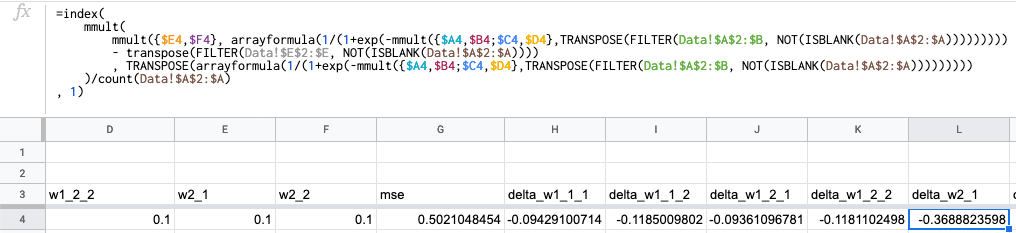
Как и для линейной регрессии: вычисляем MSE, добавляем обновление весов и протягиваем формулы:



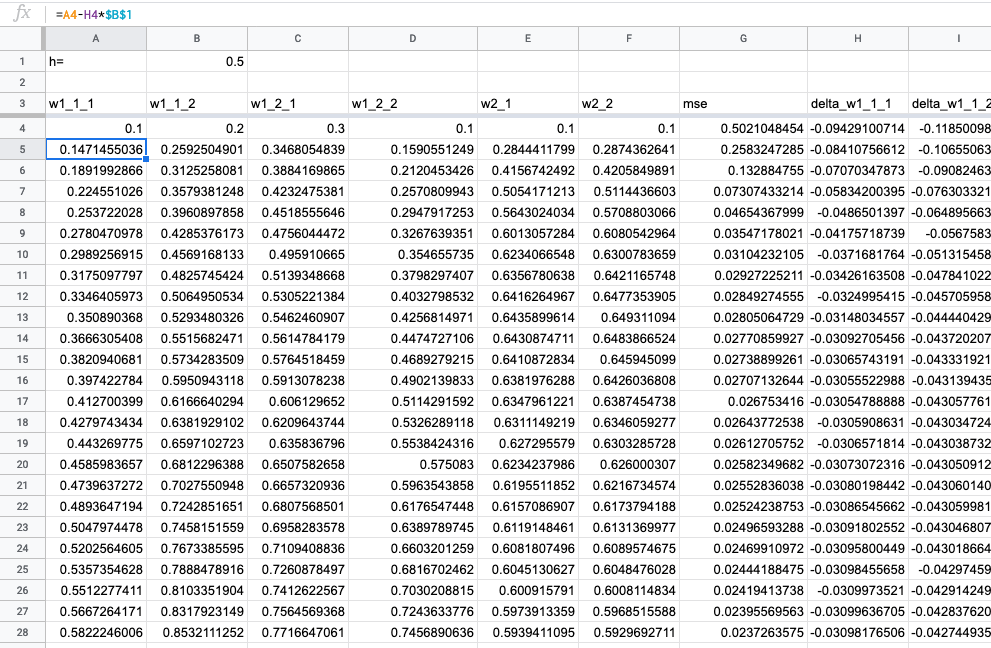
По столбцу MSE видим, что оптимизация работает.


Скопируем линейную модель и обучим ее под этот же таргет. MSE для линейной модели равно 0.025 (51-я строка), а для нейросети — 0.020 (51-я строка). На всякий случай сравним со встроенной линейной регрессией (без сдвига, так как наша нейросеть тоже без сдвига): MSE = 0.025. У нейросети меньшая ошибка, значит, эта модель лучше представляет данные. Успех!


Таблица с формулами тут: https://docs.google.com/spreadsheets/d/17gnn1kMdznEuScOsotOhrIbqMSpDLEFxkCee9Z27jRU/edit?usp=sharing


Годнота про пет-проекты на моем канале: https://t.me/just_go_right_ahead_and_do_it


P.S. Вычисляя ошибку линейной регрессии формулой LINEST, я (был очень сильно удивлен) от того, что в результат модели веса записываются в обратном порядке. То есть в первой строчке записаны коэффициенты w2, w1, bias, хотя на вход подаю в порядке x1, x2:



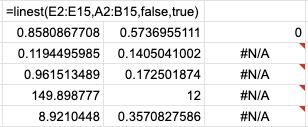
Всё бы ничего, но в документации ни слова про этот важный момент: https://support.google.com/docs/answer/3094249?hl=en. Наверняка не я один потратил время, пока разбирался с этим. Будьте внимательны.