Почти в каждой карточной игре после партии нужно перетасовать карты. Пока я тасую карты, передо мной всегда возникает вопрос: "Уже хватит?" Вопрос серьезный — лишнее время тратить не хочется, а играть на заряженной колоде тоже не в кайф.
В статье разберемся с ситуацией.

Способ тасовки
Есть крутые способы тасовать карты, riffle shuffle, например.

Я так не умею, да и картонные карты так не получится шафлить, поэтому я тасую простым способом, выглядит примерно так:

Сначала я отделяю от колоды часть, потом долю этой части закидываю на другую сторону, а после докладываю оставшуюся долю. По моим наблюдениям люди тасуют карты именно так или близко к этому. В целом, можно разделять и на большее количество частей, но это уже детали. В статье будем анализировать этот метод тасовки.
Что такое случайная раскладка карт?
Первое что пришло мне в голову — хорошая раскладка та, на i-м месте может равновероятно оказаться любая карта.
Но этого недостаточно. Например, если колоду "срезать" — разделить в случайном месте на две и поменять их местами — то первой картой равновероятно может оказаться любая. Но при этом, это, очевидно, плохая раскладка: после каждой карты, кроме нескольких, будет идти та же карта, которая лежала после нее до "среза". То есть, игрокам будут приходить "скоррелированные" карты. В случае игры в дурака одному придет та, которой били, а другому — та, которую били, и это будет совсем не случайно.
Другой подход к определению хорошей раскладки — на i+1-м месте лежит карта независимая от карты на i-м месте. Представить это можно так: если смотришь верхнюю карту колоды, то не можешь предположить какая карта будет следующей.
У этого подхода тоже могут быть проблемы, которые решаются рассмотрением больших совместных распределений, но для текущего анализа она нам полностью подойдет.
Как измерять "хорошесть" раскладки
Мы взяли колоду, оставшуюся после предыдущей игры. Занумеруем все карты по порядку. Плохая ситуация — когда после перетасовки в каком-то месте после карты с номером i идет карта с номером i+1. Поэтому будем измерять долю карт, которые лежат по порядку после перетасовки.
def next_stat(a):
c_next = 0
c_total = 0
for i in range(len(a)-1):
c_total += 1
c_next += a[i] == (a[i+1]-1)
return c_next * 1.0 / c_totalПонятно, что даже в хорошо потасованной колоде некоторые карты случайно лягут по порядку. Их доля будет в среднем 1/(n-1), где n — количество карт в колоде.
E(sum($ai = a{i+1}$ for i = 0..(n-1)) / (n-1)) = sum(E($ai = a{i+1}$) for i = 0..(n-1)) / (n-1) — из-за линейности мат. ожидания.
И так как E($ai = a{i+1}$) = 1/(n-1) то это выражение = (n-1) * 1/(n-1) / (n-1) = 1/(n-1)
Результаты
Посчитаем вероятность подряд идущих карт для колоды из 52 карт в зависимости от количества итераций перемешивания.
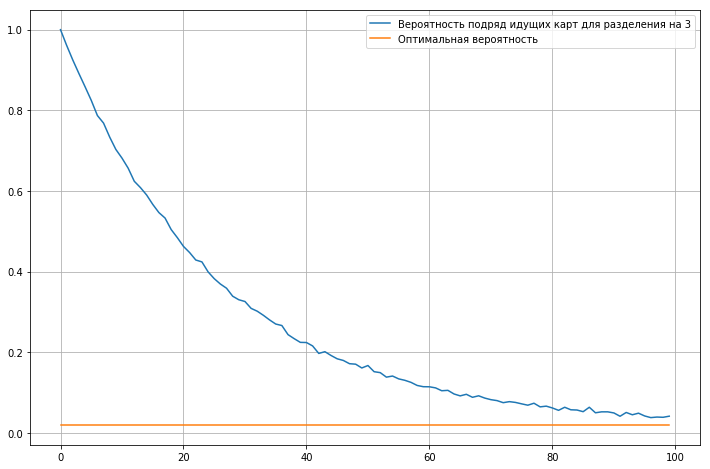
Из графика видно, что даже после сотни итераций вероятность подряд идущих карт примерно в два раза выше, чем идеальная вероятность.
import random
def two_split_shuffle(a):
s1 = random.randint(1,len(a)-1)
s2 = random.randint(1,len(a)-1)
s_min = min(s1, s2)
s_max = max(s1, s2)
p1 = a[:s_min]
p2 = a[s_min:s_max]
p3 = a[s_max:]
return p3 + p2 + p1
def shuffle_n(a, f, n):
for _ in range(n):
a = f(a)
return a
def next_stat(a):
c_next = 0
c_total = 0
for i in range(len(a)-1):
c_total += 1
c_next += a[i] == (a[i+1]-1)
return c_next * 1.0 / c_total
def expected(f, n = 100):
s = 0
for _ in range(n):
s += f()
return s / n
def get_expected_next_stat(shuf, n, cards):
return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n)))
cards = 52
x = range(100)
y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x)
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(12,8))
plt.plot(x, y, label = u'Вероятность подряд идущих карт для разделения на 3')
plt.plot(x, [1./(cards-1)] * len(x), label = u'Оптимальная вероятность')
plt.grid()
plt.legend()В целом, можно считать, что 60 итераций — оптимальное количество, меньше точно плохо. Я за 30 секунд делаю примерно 16-17 итераций. Это значит, что для нормальной перетасовки понадобится почти две минуты.
Мы с друзьями никогда столько не тасуем карты. А это значит, что у нас на игру очень сильно влияет расклад прошлой партии.
Будьте аккуратны :)
Комментарии (54)

dempfi
08.12.2019 03:56+5Эта статья могла бы быть просто великолепна если бы вы использовали математику из этой публикации https://arxiv.org/pdf/math/0501401.pdf. Jonasson в ней доказал что чтобы хорошо перетасовать колоду способом из статьи нужно минимум N^2 log N (для колоды из N карт) повторений, что чуть-чуть далеко от 64.
Кстати, эта же работа ссылается на другую работу в которой был найден самый эффективный способ тасовки — 7 итераций river shuffle.

Xobotun
08.12.2019 08:47Спасибо за ссылку. Лютый матан, конечно, аж зависть берёт. Поискал
river– не нашлось, зато на первой странице упоминаетсяriffleсо ссылкой на [1], там итераций до идеальной перетасовки 1.5log2n. Может, это оно?
dempfi
08.12.2019 12:40Riffle конечно же, автокоррекция подвела. Оценка количества итераций которую вы привели это почти она. Bayer ее уточнил по тому как люди тасуют карты и оценка чуть-чуть понизилась до тех самых 7.

Pochemuk
08.12.2019 17:23Но есть, как говорится, нюансы…
Если идеально (т.е. так, чтобы карты перемещались строго через одну) выполнить riffle shuffle над преферансной колодой (32 листа), то она вернется в исходное состояние :)
dempfi
08.12.2019 17:51Да, и это реальная проблема для тасовачных машин. Оказалось что сложно сделать машину которая будет делить колоду на две части в недетерминированном месте и тасовать ее неровно (когда каждая карта слева ложиться на каждую справа). То есть повторять «ошибки» людей, которые, в общем, и делают riffle эффективным.

DjSens
08.12.2019 08:04идеально перетасовать может смартфон или комп, напишите прогу (если такой нет): домашний комп будет сервером, гости по wi-fi подключаются и играют в карты

algotrader2013
08.12.2019 14:00домашний комп будет сервером, гости по wi-fi подключаются
Люблю старую школу… новому поколению с его облачными блокчейнами на лямбдах такого и в голову, уверен, не придет никогда)
namikiri
08.12.2019 16:46Подобными комментариями, «состаривающими» такой подход, вы делаете только хуже.

NightGhost
08.12.2019 17:50Когда ноют про новые поколения – как-то забывают, кто именно эти поколения растил и воспитывал…

Szer
08.12.2019 11:28Есть хороший выпуск намберфила по этой же теме
https://youtu.be/AxJubaijQbI
omican
08.12.2019 22:29+1Зашел в комментарии посмотреть, упомянул ли кто это видео. Именно после него я не поленился освоить riffle shuffle — это оказало несложно — и теперь тасую карты гораздо лучше.

zenkov
08.12.2019 11:32Знакомое вроде видео на картинке. Я так и не понял тогда, чувак с него прав в своих возмущениях или нет?

algotrader2013
08.12.2019 14:02Где-то обсуждали, что это вообще не проигравшийся игрок, как часто на описаниях к нему пишут, а контролер от владельца казино, который пришел причины крупного выигрыша расследовать

AC130
08.12.2019 11:56+1Что такое случайная раскладка карт?
Первое что пришло мне в голову — хорошая раскладка та, на i-м месте может равновероятно оказаться любая карта.
Но этого недостаточно. Например, если колоду «срезать» — разделить в случайном месте на две и поменять их местами — то первой картой равновероятно может оказаться любая. Но при этом, это, очевидно, плохая раскладка: после каждой карты, кроме нескольких, будет идти та же карта, которая лежала после нее до «среза». То есть, игрокам будут приходить «скоррелированные» карты. В случае игры в дурака одному придет та, которой били, а другому — та, которую били, и это будет совсем не случайно.
Другой подход к определению хорошей раскладки — на i+1-м месте лежит карта независимая от карты на i-м месте. Представить это можно так: если смотришь верхнюю карту колоды, то не можешь предположить какая карта будет следующей.
У этого подхода тоже могут быть проблемы, которые решаются рассмотрением больших совместных распределений, но для текущего анализа она нам полностью подойдет.
Кажется очевидным, что хорошая случайная тасовка колоды из n карт — та, после которой получившаяся последовательность карт является случайной величиной с равномерным распределением на множестве из n! всех возможных перестановок карт. Почему вам первым в голову пришло именно то, что написано, я не понимаю.
janatem
08.12.2019 13:38+1Тоже хотел написать именно это определение — равномерность на множестве всех перестановок. Но, справедливости ради, этот критерий технически трудно проверять (n! — это довольно много), поэтому часто используются критерии-проекции: проверить распределение отдельных карт, пар карт и т.д., в общем случае это какая-нибудь функция небольшой мощности от перестановки.

vics001
08.12.2019 15:14Если задать такое определение, то для перехода из некоторой расстановки понадобится в любую другую с одинаковой вероятностью около 20!-26! снятий (даже называть страшно), river shuffle скорее всего только в 100 раз меньше.

AC130
08.12.2019 15:31Наверное, это говорит о неэффективности используемых алгоритмов шафла карточной колоды. Ведь обычная случайная перестановка работает за линейное число операций, как уже упомянули ниже.

vp_arth
08.12.2019 13:22> Плохая ситуация — когда после перетасовки в каком-то месте после карты с номером i идет карта с номером i+1
Нормальная ситуация для нормального рандома.
Тасовка, в которой никакие пары карт никогда не сохраняют свои позиции — плохая ситуация.
____
В жизни обычно все при тасовке не перекладывают срез, а вдвигают его в оставшуюся колоду.
Карты при этом дополнительно перемешиваются, сохраняя только относительное расположение.
При такой реализации шаффла, всё перемешивается несколько быстрее.
____
Если положить колоду на стол и брать по одной карте, которую класть в случайное место в колоде в руках(которая изначально пуста), то после 52 таких итераций мы получим перетасованную колоду, равномерность которой зависит только от равномерности нашего «генератора случайного места».

Pochemuk
08.12.2019 17:14Мы с друзьями никогда столько не тасуем карты. А это значит, что у нас на игру очень сильно влияет расклад прошлой партии.
На Гамблере давно выяснено, что сгенерированная ГПСЧ «хорошо перетасованная колода» неестественна. При игре в преферанс она выдает более равномерные расклады рук, чем это случается в реальной игре.
Игроки, много играющие живую, готовы к такому отклонению от случайности и интуитивно его эксплуатируют.
Поэтому игра на Гамблере кажется им неправдоподобной.
Проводили эксперименты. В реальной игре подсчитывали число одномастных прикупов (т.е. таких, в которых обе карты одной масти). Так вот, частота таких прикупов оказывалась в 1,5-2 раза выше, чем при идеальной тасовке.
algotrader2013
08.12.2019 18:36Выходит, хороший ГПСЧ для максимального удовольствия от карточных игр должен намеренно допускать «неслучайность», и отвечать ряду статистических критериев, которые соответствуют ручной тасовке.

Pochemuk
08.12.2019 20:17+1Беда в том, что сформулировать эту «неслучайность» еще гораздо сложнее, чем идеальную случайность.
Т.е. если неудачно подобрать ее статистические характеристики, то число недовольных игроков только возрастет. А если подобрать другие характеристики, то к ним примкнут еще и новые.
А так администрация может честно ответить: Да, мы знаем, что раздачи немного не соответствуют реальным. Зато они чисто случайные и все, поэтому, в равных условиях.

yse
08.12.2019 23:19Я встречал разные подходы при игре в реальный преферанс — кто-то говорит, что надо тщательно мешать колоду (любители распасовок очевидно) и вторая крайность — вообще не мешать колоду, максимум две итерации

safari2012
09.12.2019 17:33С этой т.зрения автору статьи не мешало бы дать критерии оптимальной колоды. В Преферансе таким способом фактически не допускаются именно случайные расклады. Иначе, играть становится не интересно.

khajiit
08.12.2019 17:55Для многих игр, особенно не имеющих "карт на руке" ("Каркассон"), или малое их количество, при большом количестве вариаций ("Зельеварение", хоть с допами, хоть без), и имеющих явное деление карт на early-, mid- и endgame, актуально не просто равномерно перемешать, а еще так, чтобы не шли косяками в начале партии топовые карты.

GeBoN
08.12.2019 20:59Сначала я отделяю от колоды часть, потом долю этой части закидываю на другую сторону, а после докладываю оставшуюся долю
Обычно при тасовке используем следующий «алгоритм».
Первым движением берется часть карт из середины колоды. Потом доля этой части закидывается на верх колоды.Следующим движением колода, которая лежала на 4 пальцах руки наклоняется в сторону большого пальца и и часть взятых карт закидывается снизу колоды. И так далее, получается каждый раз часть взятых из колоды карт закидывается поочередно в вниз и верх колоды.
Конечно riffle shuffle круче, но мы так не умеем ))

saaivs
08.12.2019 22:13Перемешать что-то так, чтоб система заведомо начала демонстрировать хаотическое поведение можно с помощью, в частности,"преобразования пекаря".
Несмотря на свою простоту, преобразование пекаря очень хорошо моделирует поведение многих реальных физических систем и иллюстрирует механизм возникновения случайности в процессах, течение которых полностью предопределено.
Журнал «Квант» №4. 1989 г.
На первый взгляд, есть ощущение, что тот способ, которым большинство тасует карты — и есть его разновидность:)

dasFlug
09.12.2019 03:14С другой стороны есть же шуточное правило преферанса — «дважды сдвинутая колода считается перетасованной». В отработанной колоде чаще всего идут три карты одной масти подряд. Раздачи идет по две. И после небольшого тасования вероятность игры, а не паса, повышается, а долговременное равномерное распределение по игрокам не должно от этого сильно страдать. Игра же идеально рандомной колодой скорее всего превратится в нудную череду распасов. Но увы, матаном свое ХО я подкрепить не могу.

Pochemuk
09.12.2019 12:31Все верно. При хорошо перетасованной колоде несколько повышается вероятность ухода в распасы. При небрежно перетасованной — выше вероятность игры на взятки и/или удачного прикупа.
Это тоже замечено. В том числе при игре вживую.
Поэтому сетует на нереальность онлайновых сдач, в основном, те, кто не очень любит/умеет играть распасовки.

EvgeniyNuAfanasievich
09.12.2019 05:33а карты из новой, невскрытой пачки как-то перетасованы?
Пачки одинаково хорошо перетасованы между собой?
mao_zvezdun
09.12.2019 09:49В новой пачке карты как правило упорядочены. Я посмотрел изрядное количество видео с карточными фокусами; в тех фокусах, которые начинались с распечатки новой колоды и подчеркивалось, что они упорядочены стандартным образом, использовался такой порядок. Начинается с туза масти пик, потом от двойки до десятки, валет, дама, король, потом такой же порядок с мастью бубен, потом трефы в обратном порядке от короля до туза и такой же обратный порядок от короля до туза червей. То есть начинается и заканчивается тузами, а в середине колоды два короля («kissing kings»). Рекламные карты и джокеры отдельно в самом начале.

vesper-bot
09.12.2019 11:21Нет, лежат в порядке 23456… КА с каким-то порядком мастей. Так удобнее фасовать.

asm0dey
09.12.2019 08:59Riffle shuffle это просто! Я прямо рекомендую освоить, меньше дня на освоение. Ну и нормальной колодой играть удобнее конечно.

frobeniusfg
09.12.2019 09:58Индийская тасовка (hindu shuffle), пожалуй, быстрее делается.

SandroSmith
10.12.2019 10:47Но ведь она ничем принципиально не отличается от тасовки из второй гифки статьи. Только хват другой.

BiW
09.12.2019 10:15Совет от человека, до недавнего времени работавшего в игровой индустрии. Идеальная тасовка — это та, когда вы карты вообще в руки не берете, либо берете но играете, без каких либо ставок.

opckSheff
09.12.2019 11:20То есть если дома в дурака на интерес играете, по вашей логике можно карты вообще не тасовать, тасовка уже идеальная.

Darlington
09.12.2019 12:32Способ далеко не лучший. Когда мы берём колоду, мы её делим примерно в соотношении 50/50, потом половину от первой колоды мы так же делим и соединяем со второй пока первая колода не будет содержать 1-3 карты. Потом повторяем. Из-за того, что остаются подпоследовательности исходной колоды, то «корреляция» с исходной колодой будет всегда существовать. Самый надёжный способ это разбросать карты по столу, перемешать и собрать в колоду, тогда все пары исходной колоды будут разорваны, а те же самые пары в новой колоде будут более случайны.
Почему бы не рассмотреть этот вопрос с точки зрения энтропии?

QDeathNick
09.12.2019 14:02В случае игры в дурака одному придет та, которой били, а другому — та, которую били, и это будет совсем не случайно.
А меня бабушка приучила сдавать всегда по две карты. Видимо как раз для того чтобы не было такого попадания. Я редко, но сталкивался с людьми, которые тоже сдавали парами.
Компьютеры убили карты, раньше без карт и недели не проходило, а теперь хорошо если раз в год пуля.
Pochemuk
09.12.2019 14:50Компьютеры убили карты, раньше без карт и недели не проходило, а теперь хорошо если раз в год пуля.
В студенческие годы вечера не проходило, чтобы не расписать одну-две пульки :) Кроме, разве что, сессии.

safari2012
09.12.2019 17:43В преф именно так и сдаётся, именно, чтобы избежать случайного расклада. Полностью случайных раскладов в префе быть не должно, должны быть перекосы в мастях, иначе играть будет не интересно/долго.


Narical
Вопрос решается раскладыванием карт на несколько стопок, после чего складыванием их вместе и тасовкой. Несколько итераций можно секунд за 30 сделать.
xtreye
Вопрос решается недорогой машинкой с AliExpress :)
Mylistryx
ShuffleMachine если на то пошло. IoT убъет их, хотя изначально — статистика!
progman_rus
недорогя шаффл машинка с алиэкспресс не перетасует карты хорошо ( проверено ).
Только профф модели от 500$ и выше
Mylistryx
Среднестатистически мы имеем ShuffleMachine за 500$ и выше, фактически мы имеем пару маргиналов у которых режим «Shuffle» отключается после опохмелья. Так себе тоже механизм. Но у этих механизмов random не псевдослучаен!
v1000
где-то была новость про то, как один человек разгадал псевдовероятность таких машинок, а так как в казино в начале партии распечатывали новую колоду, то можно было высчитать результат перетасовки.
progman_rus
Врут. Без вмешательства в прошивку шафлмашины сие невозможно.
Они все проходят сертификацию ( что то типа RNG Certification )