Содержание

Часть 1: Введение.
Часть 2: Аппаратное обеспечение GPU и шаблоны параллельной коммуникации.
Часть 3: Фундаментальные алгоритмы GPU: свертка (reduce), сканирование (scan) и гистограмма (histogram).
Часть 4: Фундаментальные алгоритмы GPU: уплотнение (compact), сегментированное сканирование (segmented scan), сортировка. Практическое применение некоторых алгоритмов.
Часть 5: Оптимизация GPU программ.
Часть 6: Примеры параллелизации последовательных алгоритмов.
Часть 7: Дополнительные темы параллельного программирования, динамический параллелизм.

Количество шагов (steps) vs количество операций (work)

Многие читатели хабра наверняка знакомы с нотацией большого О, используемой для оценки времени работы алгоритмов. Например, говорят что время работы алгоритма сортировки слиянием может быть оценено как O(n*log(n)). На самом деле, это не совсем корректно: правильней было бы сказать, что время работы этого алгоритма при использовании одного процессора или общее количество операций может быть оценено как O(n*log(n)). Для пояснения рассмотрим дерево выполнения алгоритма:

Итак, мы начинаем с несортированного массива из n элементов. Далее, делается 2 рекурсивных вызова для сортировки левой и правой половины массива, после чего выполняется слияние отсортированных половин, которое выполняется за O(n) операций. Рекурсивные вызовы будут выполняться пока размер сортируемой части не станет равен 1 — массив из одного элемента всегда отсортирован. Значит, высота дерева — O(log(n)) и на каждом его уровне выполняется O(n) операций (на 2-м уровне — 2 слияния по O(n/2), на 3-м — 4 слияния по O(n/4) и т.д.). Итого — O(n*log(n)) операций. Если у нас есть только один процессор (под процессором понимается некоторый абстрактный обработчик, а не CPU) — то это также и оценка времени выполнения алгоритма. Однако, предположим что мы каким-то образом смогли бы выполнять слияние параллельно несколькими обработчиками — в лучшем случае, мы бы разделили O(n) операций на каждом уровне так, чтобы каждый обработчик выполнял константное количество операций — тогда каждый уровень будет выполняться за O(1) времени, а оценка времени выполнения всего алгоритма станет равна O(log(n))!
Говоря простым языком, количество шагов будет равно высоте дерева выполнения алгоритма (при условии, что операции одного уровня могут выполняться независимо друг от друга — поэтому в стандартном виде количество шагов алгоритма сортировки слиянием не равно O(log(n)) — операции одного уровня не независимы), ну а количество операций — количеству операций:) Таким образом, при программировании на GPU имеет смысл использовать алгоритмы с меньшим количеством шагов, иногда даже за счет увеличения общего количества операций.
Далее рассмотрим разные реализации 3 фундаментальных алгоритмов параллельного программирования и проанализируем их с точки зрения количества шагов и операций.

Свертка (reduce)

Операция свертки выполняется над некоторым массивом элементов и определяется оператором свертки. Оператор свертки должен быть бинарным и ассоциативным — то-есть принимать на вход 2 элемента и удовлетворять равенству a*(b*c)=(a*b)*c, где * — обозначение оператора (не путать со свойством коммутативности a*b=b*a). Операция свертки над массивом из элементов a₁,...,a_n определяется как (...((a₁*a₂)*a₃)...*a_n). Дерево выполнения последовательного алгоритма для реализации операции свертки имеет следующий вид:

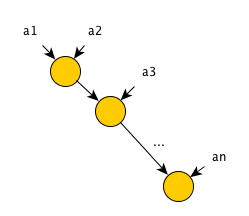
Очевидно, что для данного алгоритма количество операций равно количеству шагов и равно n-1=O(n).
Для «параллелизации» алгоритма достаточно учесть свойство ассоциативности оператора свертки, и переставить скобки местами: (...((a₁*a₂)*a₃)...*a_n)=(a₁*a₂)*(a₃*a₄)*...*(a_n-1*a_n). То-есть, мы можем параллельно посчитать значения (a₁*a₂), (a₃*a₄) и так далее, после чего произвести операцию свертки на результирующих значениях. Дерево выполнения такого алгоритма:

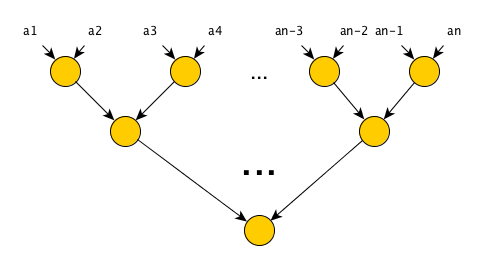
Количество шагов теперь равно O(log(n)), количество операций — O(n), что не может не радовать — с помощью простой перестановки скобок мы получили алгоритм со значительно меньшим количеством шагов при этом количество операций осталось прежним!

Сканирование (scan)

Операция сканирования тоже выполняется над массивом элементов, но определяется оператором сканирования и единичным элементом (identity element). Оператор сканирования должен удовлетворять тем же требованиям, что и оператор свертки; единичный элемент же должен обладать свойством I*a=a, где I — единичный элемент, * — оператор сканирования и a — любой другой элемент. Например, для оператора сложения единичным элементом будет 0, для оператора умножения — 1. Результатом применения операции сканирования к массиву элементов a₁,...,a_n будет массив такой же размерности n. Различают два вида операции сканирования:

1. Включающее сканирование — результат рассчитывается как: [reduce([a₁]), reduce([a₁,a₂]), ..., reduce([a₁,...,a_n])] — на месте i-го входного элемента в выходном массиве будет стоять результат применения операции свертки всех предыдущих элементов включая сам i-ый элемент.
2. Исключающее сканирование — результат рассчитывается как: [I, reduce([a₁]), ..., reduce([a₁,...,a_n-1])] — на месте i-го входного элемента в выходном массиве будет стоять результат применения операции свертки всех предыдущих элементов исключая сам i-ый элемент — по-этому первым элементом выходного массива будет единичный элемент.

Операция сканирования не настолько полезна сама по себе, однако она является одним из этапов многих параллельных алгоритмов. Если у вас под руками есть реализация только включающего сканирования а вам нужно исключающее — просто передайте массив [I, a₁, ..., a_n-1] вместо массива [a₁, ..., a_n]; если наоборот — передайте массив [a₁, ..., a_n, I] и выкиньте из результирующего массива первый элемент. Таким образом, оба вида сканирования взаимозаменяемы. Дерево выполнения последовательной реализации операции сканирования будет выглядеть так же, как и дерево выполнения операции свертки — просто перед каждой вершиной дерева мы будем записывать текущий результат свертки (a₁ перед первым вычислением для включающего сканирования и I для исключающего) в соответствующую позицию выходного массива.
Следовательно, количество шагов и операций такого алгоритма будут равны n-1=O(n).
Наиболее простой способ уменьшить количество шагов алгоритма довольно прямолинейный — так как операция сканирования по сути определяется через операцию свертки, что нам мешает просто n раз запустить параллельный вариант операции свертки? Количество шагов в таком случае действительно снизится — так как все свертки могут быть рассчитаны независимо, то общее количество шагов определяется сверткой с наибольшим количеством шагов — а именно самой последней, которая будет рассчитана на всем входном массиве. Итого — O(log(n)) шагов. Однако, количество операций такого алгоритма удручает — первая свертка потребует 0 операций (не учитывая операций с памятью), вторая — 1, ..., последняя — n-1 операций, итого — 1+2+...+n-1=(n-1)*(n)/2=O(n²).
Рассмотрим 2 более эффективных с точки зрения количества операций алгоритма выполнения операции сканирования. Авторы первого алгоритма — Daniel Hillis и Guy Steele, алгоритм назван в их честь — Hills & Steele scan. Алгоритм очень простой, и может быть записан в 6 строчках питонопсевдокода:

def hillie_steele_scan(io_arr):
    N = len(io_arr)
    for step in range(int(log(N, 2))+1):
        dist = 2**step
        for i in range(N-1, dist-1, -1):
            io_arr[i] = io_arr[i] + io_arr[i-dist]

Или словами: начиная с шага 0 и заканчивая шагом log₂(N) (откидывая дробную часть), на каждом шаге step каждый элемент под индексом i обновляет свое значение как a[i]=a[i]+a[i-2^step] (естественно, если 2^step <= i). Если в уме проследить выполнение этого алгоритма для какого-то массива становится понятно, почему он корректен: после шага 0 каждый элемент будет содержать сумму себя и одного соседнего элемента слева; после шага 1 — сумму себя и 3 соседних элементов слева… на шаге n — сумму себя и 2ⁿ⁺¹-1 элементов слева — очевидно, что если количество шагов равно целой части log₂(N), то после последнего шага мы получим массив, соответствующий выполнению операции включающего сканирования. Из описания алгоритма очевидно, что количество шагов равно log₂(N)+1=O(log(n)). Количество операций равно (N-1)+(N-2)+(N-4)...+(N-2^log₂(N))=O(N*log(N)). Дерево выполнения алгоритма на примере массива из 8 элементов и оператора суммы выглядит так:

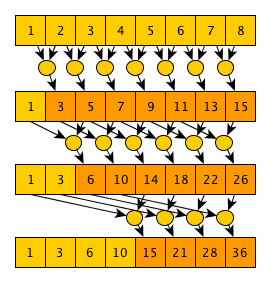
Автор второго алгоритма — Guy Blelloch, алгоритм называется (кто бы подумал) — Blelloch scan. Данный алгоритм реализует исключающее сканирование и сложнее предыдущего, однако требует меньшего количества операций. Основная идея алгоритма в том, что если внимательно посмотреть на реализацию параллельного алгоритма свертки, то можно заметить, что по ходу вычисления конечного значения мы также рассчитываем много полезных промежуточных значений, например после 1-го шага — значения a₁*a₂,a₃*a₄,...,a_n-1*a_n, после 2-го шага — значения a₁*a₂*a₃*a₄,a₅*a₆*a₇*a₈... и так далее. И если эти значения не выкидывать, то мы можем очень быстро рассчитать, например, свертку первых шести элементов — достаточно взять уже рассчитанные значения свертки первых 4 элементов и элементов a₅,a₆ и «свернуть» их. Поэтому алгоритм состоит из 2-х фаз — собственно, фаза свертки, и вторая фаза, называемая down-sweep (что-то вроде «развертка вниз»). Графически, первая фаза выглядит следующим образом (на примере все тех же массива из 8 элементов и оператора суммы):

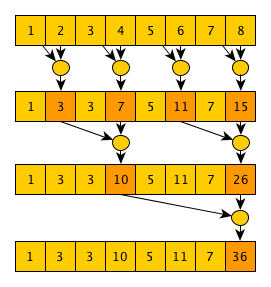
То-есть практически обычный алгоритм свертки, только промежуточные свертки, посчитанные над элементами a_i,a_i+1,...,a_i+k заменяют элемент a_i+k в массиве.
Вторая фаза является практически зеркальным отображением первой, но использоваться будет «специальный» оператор, который возвращает 2 значения, и в начале фазы последнее значение массива заменяется на единичный элемент (0 для оператора сложения):

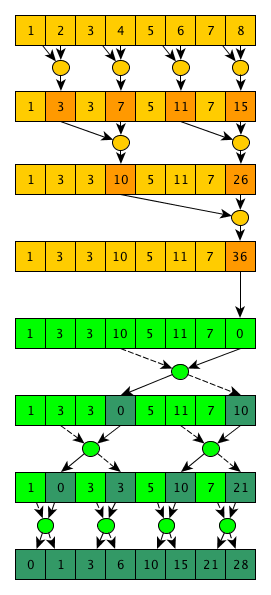
Этот «специальный» оператор принимает 2 значения — левое и правое, при этом в качестве левого выходного значения он просто возвращает правое входное, а в качестве правого выходного — результат применения оператора сканирования к левому и правому входным значениям. Все эти манипуляции нужны для того, чтобы в итоге корректно свернуть посчитанные промежуточные свертки и получить желаемый результат — исключающее сканирование входного массива. Как отлично видно из этой иллюстрации работы алгоритма, общее количество операций равно N-1+N-1+N-1=O(N), а количество шагов равно 2*log₂(N)=O(log(N)). Как обычно, за все хорошее (улучшенную асимптотику в данном случае) приходится платить — алгоритм не только более сложный в псевдокоде, но его также сложнее эффективно реализовать на GPU — на первых шагах алгоритма мы имеем довольно много работы, которую можно выполнять параллельно; при приближении к концу первой фазы и в начале второй фазы на каждом шаге будет выполняться совсем мало работы; и в конце второй фазы мы опять будем иметь много работы на каждом шаге (кстати, такой шаблон выполнения имеют еще несколько интересных параллельных алгоритмов). Одно из возможных решений этой проблемы — написание 2-х разных ядер — одно будет выполнять только один шаг, и использоваться в начале и в конце выполнения алгоритма; второе будет рассчитано на выполнение нескольких шагов подряд и будет использоваться в середине выполнения — на переходе между фазами. Ну а на стороне хоста будет определяться, какое ядро вызывать сейчас в зависимости от количества работы, которую необходимо выполнить на текущем шаге.

Гистограмма (histogram)

Неформально, под гистограммой в контексте программирования GPU (и не только) понимают распределение массива элементов по массиву ячеек, где каждая ячейка может содержать только элементы с определенными свойствами. Например, имея данные о баскетболистах, такие как рост, вес и тд. мы хотим узнать сколько баскетболистов имеют рост <180 см., от 180 см. до 190 см. и >190 см.
Как обычно, последовательный алгоритм вычисления гистограммы довольно простой — просто пройтись по всем элементам в массиве, и для каждого элемента увеличить на 1 значение в соответствующей ему ячейке. Количество шагов и операций — O(N).
Самый простой параллельный алгоритм вычисления гистограммы — запустить по потоку на элемент массива, и каждый поток будет увеличивать значение в ячейке только для своего элемента. Естественно, в этом случае необходимо использовать атомарные операции. Недостаток этого метода — скорость. Атомарные операции заставляют потоки синхронизировать доступ к ячейкам и при увеличении количества элементов эффективность данного алгоритма будет падать.
Один из способов, позволяющий избежать использования атомарных операций при построении гистограммы, заключается в использовании отдельного набора ячеек для каждого потока и последующей свертки этих локальных гистограмм. Недостаток — при большом количестве потоков нам может элементарно не хватить памяти для хранения всех локальных гистограмм.
Еще один вариант повысить эффективность простейшего алгоритма учитывает специфику CUDA, а именно что мы запускаем потоки в блоках, которые имеют общую память, и мы можем сделать общую гистограмму для всех потоков одного блока, а в конце выполнения ядра с помощью все тех же атомарных операций добавить эту гистограмму к глобальной. И хотя для построения общей гистограммы блока все равно необходимо использовать атомарные операции над общей памятью блока, они значительно быстрее атомарных операций над глобальной памятью.

Заключение

Данная часть описывает основные примитивы многих параллельных алгоритмов. Практическая реализация большинства этих примитивов будет показана в следующей части, где в качестве примера мы напишем поразрядную сортировку.