Привет, Хабр! Сегодня хочу поделиться небольшим примером того, как можно проводить кластерный анализ. В этом примере читатель не найдет нейронных сетей и прочих модных направлений. Данный пример может служить точкой отсчета для того, чтобы сделать небольшой и полный кластерный анализ для других данных. Всем заинтересованным — добро пожаловать под кат.
Сразу оговорюсь, эта статья ни в коем случае не претендует на академическую полноту, уникальность полученных результатов или полноту освещения вопроса. Статья призвана продемонстрировать основные шаги классического кластерного анализа, которые могут быть использованы для простого и осмысленного (возможно, предваряющего более детальное) исследования. Любые исправления, замечания и дополнения по существу приветствуются.
Данные представляют собой выборку потребления алкоголя по странам на душу населения по типу алкогольных напитков (пиво, вино, спиртные напитки и др.) за 2010 год в процентах от потребления алкоголя на душу населения. Также данные содержат: среднее суточное потребление алкоголя на душу населения в граммах чистого алкоголя и всё (зарегистрировано + неучтенное) потребление алкоголя на душу населения (только пьющие в литрах чистого алкоголя).
В то же время каждая страна условно относится к одной из географических групп: восток, центр и запад. Разделение весьма условное и очень спорное по разным причинам, но будем отталкиваться от того, что есть. Источник данных — Global status report on alcohol and health 2014, С. 289-364
(Раскрашивал вручную, могут быть погрешности, но общая мысль, думаю, понятна)
Предварительный анализ
Подключим используемые библиотеки.
library(rgl)
library(heplots)
library(MVN)
library(klaR)
library('Morpho')
library(caret)
library(mclust)
library(ggplot2)
library(GGally)
library(plyr)
library(psych)
library(GPArotation)
library(ggpubr)Загрузим данные и посмотрим, как они выглядят.
# Загружаем данные из файла
data <- read.table("alcohol_data.csv", header=TRUE, sep=",")
# Делаем из первого столбца названия строк
rownames(data) <- make.names(data[,1], unique = TRUE)
# Записываем данные и удаляем пропуска, если они есть
data <- data[,-1]
data <- na.omit(data)
# Выводим несколько первых строчек
head(data)| Beer | Wine | Spirit | Other | Total | Average_daily | Group | |
|---|---|---|---|---|---|---|---|
| Albania | 31.8 | 19.8 | 48.4 | 0.0 | 13.0 | 27.5 | center |
| Armenia | 9.7 | 5.3 | 84.9 | 0.0 | 8.3 | 17.9 | east |
| Austria | 50.4 | 35.5 | 14.0 | 0.0 | 13.8 | 29.6 | center |
| Azerbaijan | 28.7 | 7.6 | 63.3 | 0.0 | 5.2 | 11.1 | east |
| Belarus | 17.3 | 5.2 | 46.6 | 30.9 | 22.1 | 48.0 | east |
| Belgium | 49.2 | 36.3 | 14.4 | 0.1 | 12.8 | 27.7 | center |
| ... | ... | ... | ... | ... | ... | ... | ... |
Посчитаем стандартные статистики
summary(data)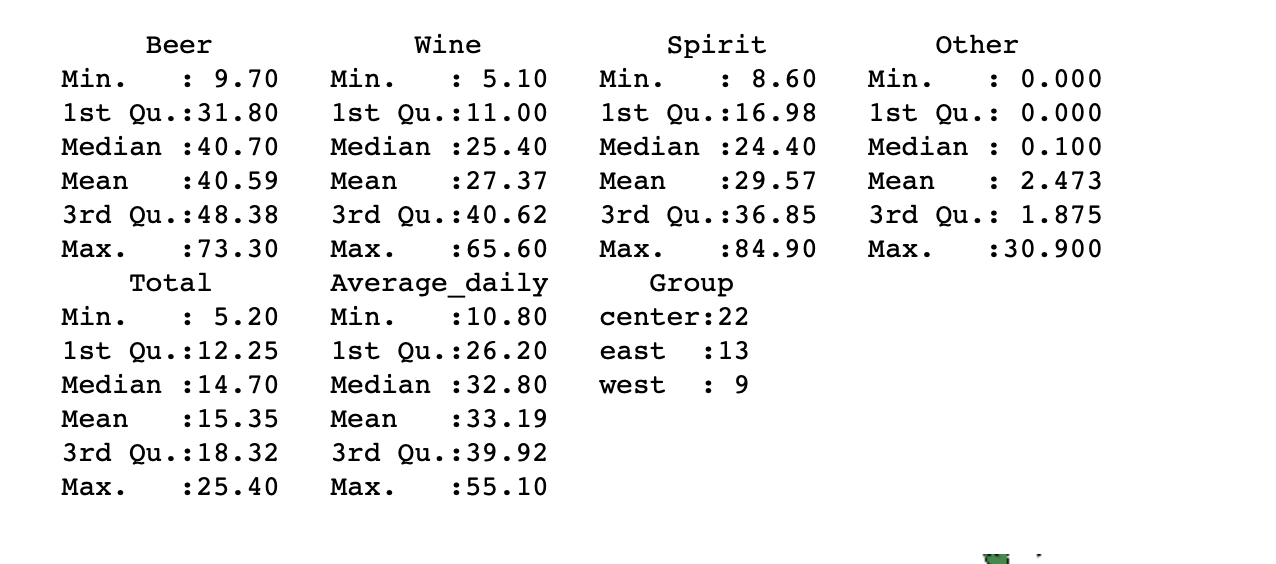
Глядя на эти статистики, можно многое сказать о характере данных. Например, что у Other очень большой разброс, и максимум сильно отстоит от третьего квартиля, значит, там есть как минимум одно сильно отличающееся наблюдение, так называемый выброс. Также видно по первому квартилю и среднему, что в этом столбце существенное количество нулевых значений, что, скорее всего, связано с недостатком данных. Также сразу видим сколько стран в каждой из групп, группы не сбалансированны по количеству. Аналогично можно рассматривать и статистики по другим признакам и делать какие-то полезные выводы и предположения.
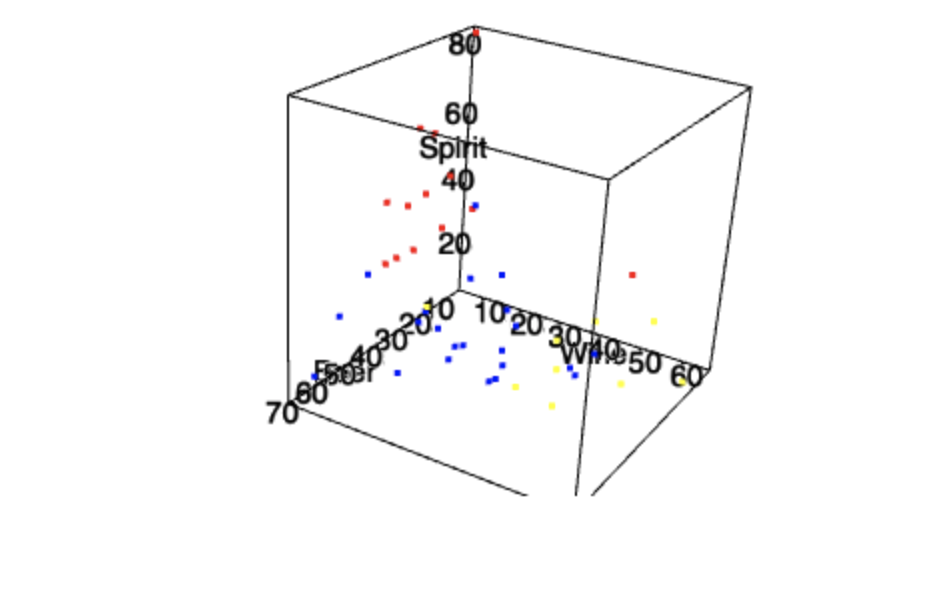
Если, как в нашем случае, у вас три основные переменные, можно попробовать отразить их на трехмерном графике.
options(rgl.useNULL=TRUE)
open3d()
mfrow3d(2,2)
levelColors <- c('west'='blue', 'east'='red', 'center'='yellow')
plot3d(data$Beer, data$Wine, data$Spirit, xlab="Beer", ylab="Wine", zlab="Spirit", col = levelColors[data$Group], size=3)
widget <- rglwidget()
widgetПолучаются довольно наглядные графики, которые можно покрутить и помасштабировать интерактивно. Судя по этому графику понятно, что по этим трем признакам группы визуально различаются.
Посмотрим эмпирические плотности по группам
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
upper = list(continuous = wrap("cor", alpha = 0.5), combo = "box"),
lower = list(continuous = wrap("points", alpha = 0.3), combo = wrap("dot", alpha = 0.4)),
diag = list(continuous = wrap("densityDiag",alpha = 0.5)),
title = "Alcohol"
)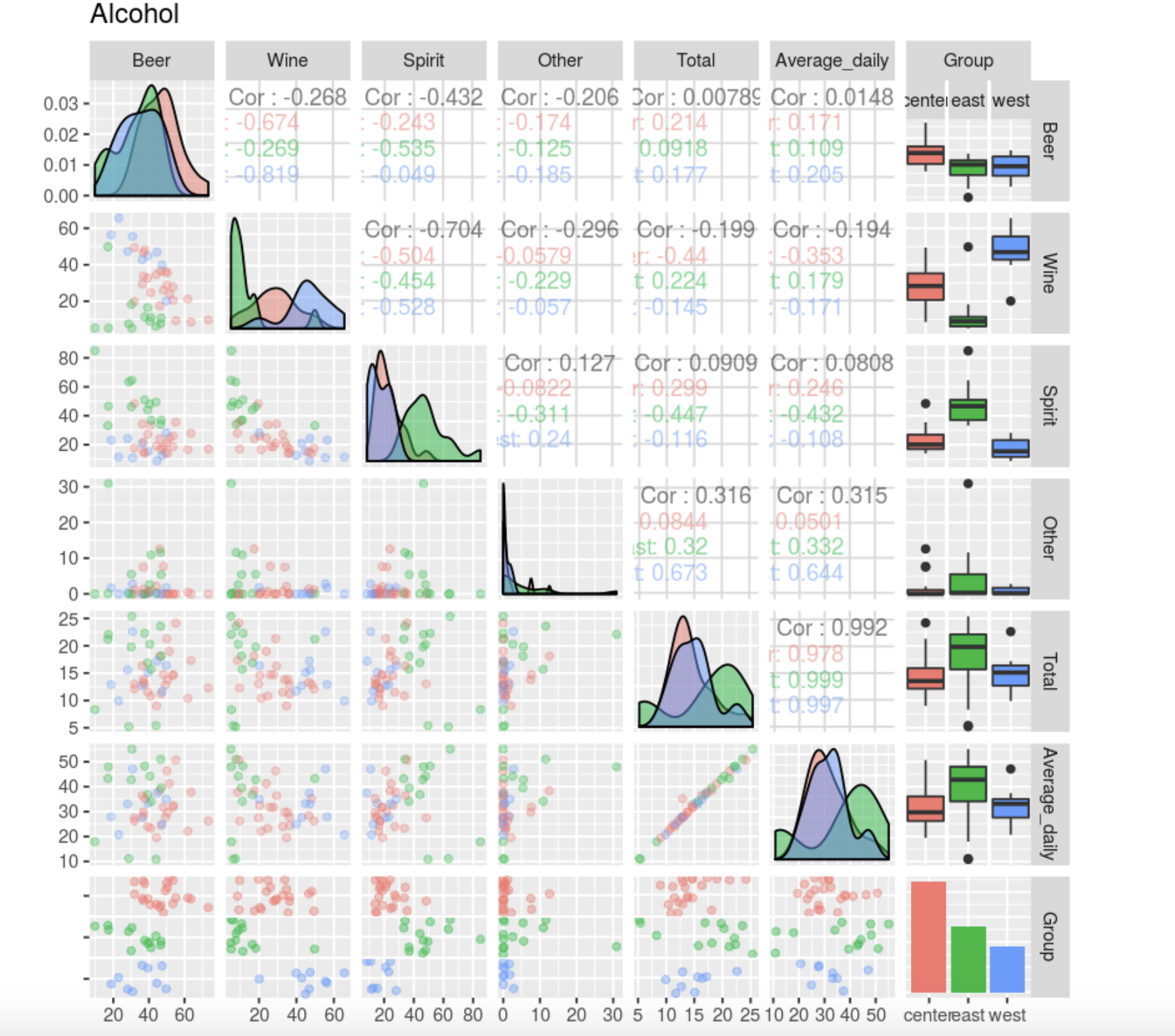
Так как Average и Total сильно коррелируют, исключим из рассмотрения Average.
data <- data[, -6]У нас несколько групп, и не только предполагается, а даже видно, что они разные, поэтому нужно рассматривать распределение отдельно по группам. Посмотрим отличающиеся данные по группам.
data[data$Wine>60,]
| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Italy | 23 | 65.6 | 11.5 | 0 | 9.9 | west |
В том что итальянцы пьют вина больше всех, даже без учета разделения на группы, думаю, нет ничего удивительного, поэтому из-за того, что и так мало данных, оставим это наблюдение.
data[data$Spirit>70,]
data[data$Spirit<10,]| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Armenia | 9.7 | 5.3 | 84.9 | 0 | 8.3 | east |
| Beer | Wine | Spirit | Other | Total | Group | |
|---|---|---|---|---|---|---|
| Slovenia | 44.5 | 46.9 | 8.6 | 0 | 17.2 | west |
Весьма подозрительные данные относительно выборки, пока оставим их, но будем иметь в виду.
Данных не так много, поэтому посмотрим на данные по группам
split(data[,1:5],data$Group)$center
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Albania | 31.8 | 19.8 | 48.4 | 0.0 | 13.0 |
| Austria | 50.4 | 35.5 | 14.0 | 0.0 | 13.8 |
| Belgium | 49.2 | 36.3 | 14.4 | 0.1 | 12.8 |
| Bosnia.and.Herzegovina | 73.3 | 9.7 | 17.0 | 0.0 | 12.3 |
| Cyprus | 40.9 | 24.7 | 33.7 | 0.7 | 10.8 |
| Czech.Republic | 53.5 | 20.5 | 26.0 | 0.0 | 14.6 |
| Denmark | 37.7 | 48.2 | 14.1 | 0.0 | 12.9 |
| Finland | 46.0 | 17.5 | 24.0 | 12.6 | 18.1 |
| Germany | 53.6 | 27.8 | 18.6 | 0.0 | 14.7 |
| Hungary | 36.3 | 29.4 | 34.3 | 0.0 | 16.3 |
| Iceland | 61.8 | 21.2 | 16.5 | 0.5 | 10.4 |
| Ireland | 48.1 | 26.1 | 18.7 | 7.7 | 14.7 |
| Malta | 39.4 | 32.7 | 27.2 | 0.7 | 11.5 |
| Netherlands | 46.8 | 36.4 | 16.9 | 0.0 | 11.2 |
| Norway | 44.2 | 34.7 | 19.0 | 2.1 | 9.0 |
| Poland | 55.1 | 9.3 | 35.5 | 0.0 | 24.2 |
| Romania | 50.0 | 28.9 | 21.1 | 0.0 | 21.3 |
| Serbia | 51.5 | 23.9 | 24.6 | 0.0 | 19.0 |
| Sweden | 37.0 | 46.6 | 15.1 | 1.4 | 13.3 |
| Switzerland | 31.8 | 49.4 | 17.6 | 1.2 | 12.1 |
| Turkey | 63.6 | 8.6 | 27.9 | 0.0 | 17.3 |
| UK | 36.9 | 33.8 | 21.8 | 7.5 | 13.8 |
$east
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Armenia | 9.7 | 5.3 | 84.9 | 0.0 | 8.3 |
| Azerbaijan | 28.7 | 7.6 | 63.3 | 0.0 | 5.2 |
| Belarus | 17.3 | 5.2 | 46.6 | 30.9 | 22.1 |
| Bulgaria | 39.3 | 16.5 | 44.1 | 0.1 | 16.9 |
| Estonia | 41.2 | 11.1 | 36.8 | 10.9 | 15.7 |
| Georgia | 17.0 | 49.8 | 33.2 | 0.1 | 21.2 |
| Israel | 44.0 | 6.2 | 49.5 | 0.3 | 5.4 |
| Latvia | 46.9 | 10.7 | 37.0 | 5.4 | 18.1 |
| Lithuania | 46.5 | 7.8 | 34.1 | 11.6 | 23.6 |
| Republic.of.Moldova | 30.4 | 5.1 | 64.5 | 0.0 | 25.4 |
| Russian.Federation | 37.6 | 11.4 | 51.0 | 0.0 | 22.3 |
| Slovakia | 30.1 | 18.3 | 46.2 | 5.5 | 19.8 |
| Ukraine | 40.5 | 9.0 | 48.0 | 2.6 | 20.3 |
$west
| Beer | Wine | Spirit | Other | Total | |
|---|---|---|---|---|---|
| Croatia | 39.5 | 44.8 | 15.4 | 0.2 | 15.1 |
| France | 18.8 | 56.4 | 23.1 | 1.7 | 12.9 |
| Greece | 28.1 | 47.3 | 24.2 | 0.4 | 15.6 |
| Italy | 23.0 | 65.6 | 11.5 | 0.0 | 9.9 |
| Luxembourg | 36.2 | 42.8 | 21.0 | 0.0 | 12.7 |
| Portugal | 30.8 | 55.5 | 10.9 | 2.8 | 22.6 |
| Slovenia | 44.5 | 46.9 | 8.6 | 0.0 | 17.2 |
| Spain | 49.7 | 20.1 | 28.2 | 1.8 | 16.4 |
| Republic.of.Macedonia | 47.4 | 39.9 | 12.6 | 0.0 | 11.7 |
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
diag=list(continuous="bar", alpha=0.4)
)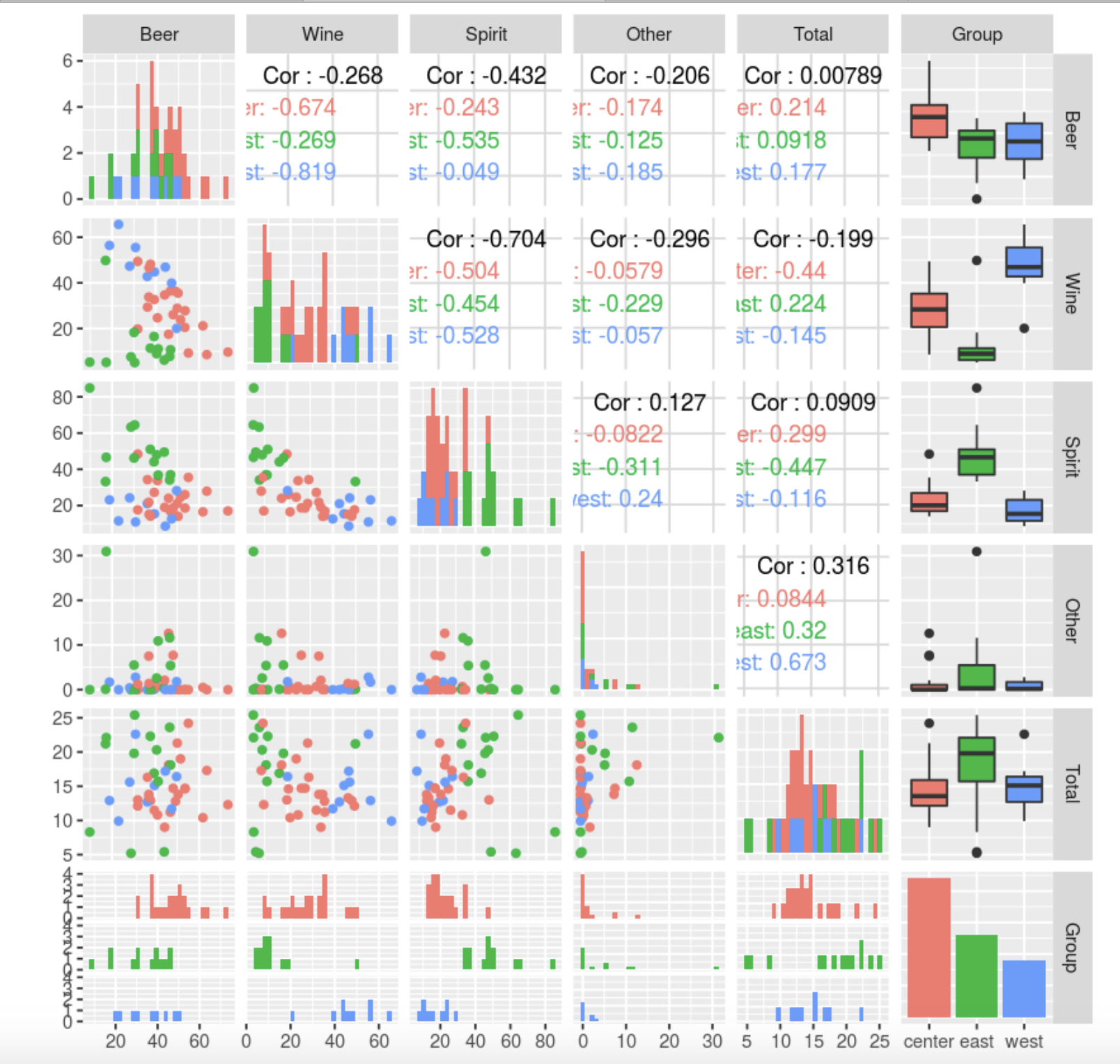
Из гистограмм видно, что группы лучше всего различаются по пиву, вину и спиртным напиткам. Если брать признак Other, заметим: мало того, что у него весьма странное распределение, так еще и в большинстве стран маленькие и даже нулевые значения, кроме нескольких (примерно 10-12 стран, а так как индивидов всего 45, исключив их, мы существенно сократим объем данных). Больше всего отличается Республика Беларусь. Немного подумав, можно сделать предположение, что там предпочитают крамбамбуля вместо пива, вина и спиртных напитков (шутка). Ну, а если более формально, то скорее всего это связано с неполнотой исходных данных или несовершенством регистрации данных. Уберем признак Other из рассмотрения.
Также на гистограммах можно заметить, что для центра превалирует пиво, для запада — вино, а для востока — спиртные напитки. Это вполне укладывается в общеизвестные представления, можно даже сказать — стереотипы, о культуре потребления спиртных напитков в этих регионах.
На диаграммах рассеяния признака Total и Other, визуально группы не выделяются. Будем иметь этот факт в виду в дальнейшем.
Примечательно, что между признаками Beer, Spirit и Wine отрицательные корреляции. Возможно, это также относится к тому, что по этим переменным можно выделять группы предпочтения в алкоголе, и они будут близки к географическим. После того как изучили данные, получили некие априорные представления, убрали лишние, на наш взгляд, признаки, перейдем к кластерному анализу.
Кластерный анализ
Уберем разметку данных на группы и уберем признак Total. Это позволит не нормировать данные, так как остальные признаки — в одной шкале.
data.group = data[,5]
data <- data[,-5]
data<- data[,-4]Определим число кластеров Elbow method (“метод согнутого колена”, он же “метод каменистой осыпи”). Построим график, где по оси абсцисс отмечено число кластеров k, а по оси ординат – значения функции W(K), которая определяет внутригрупповой разброс в зависимости от числа кластеров.
library(factoextra)
fviz_nbclust(data, kmeans, method = "wss") +
labs(subtitle = "Elbow method") +
geom_vline(xintercept = 4, linetype = 2)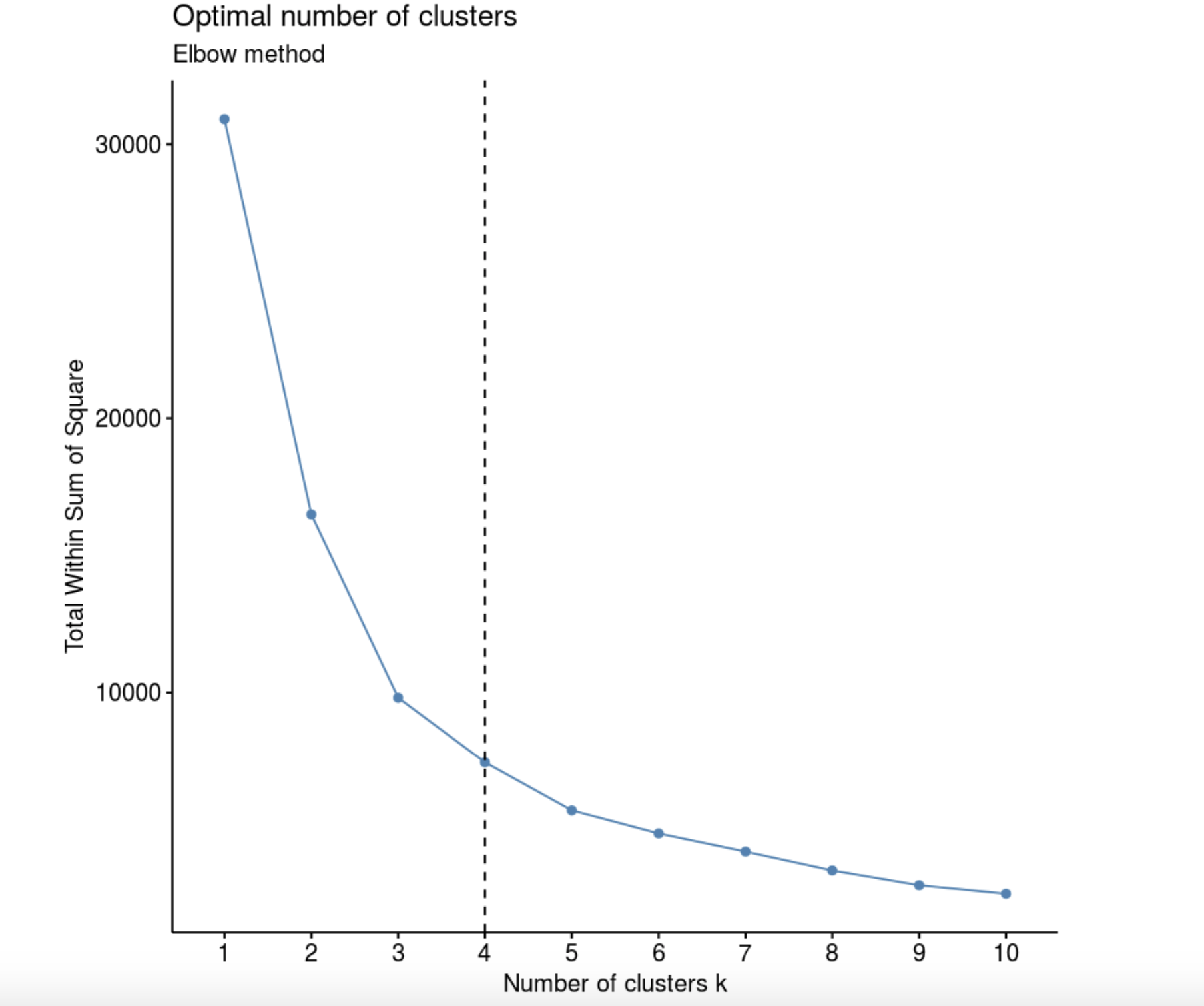
data.dist <- dist((data))
hc <- hclust(data.dist, method = "ward.D2")
plot(hc, cex = 0.7)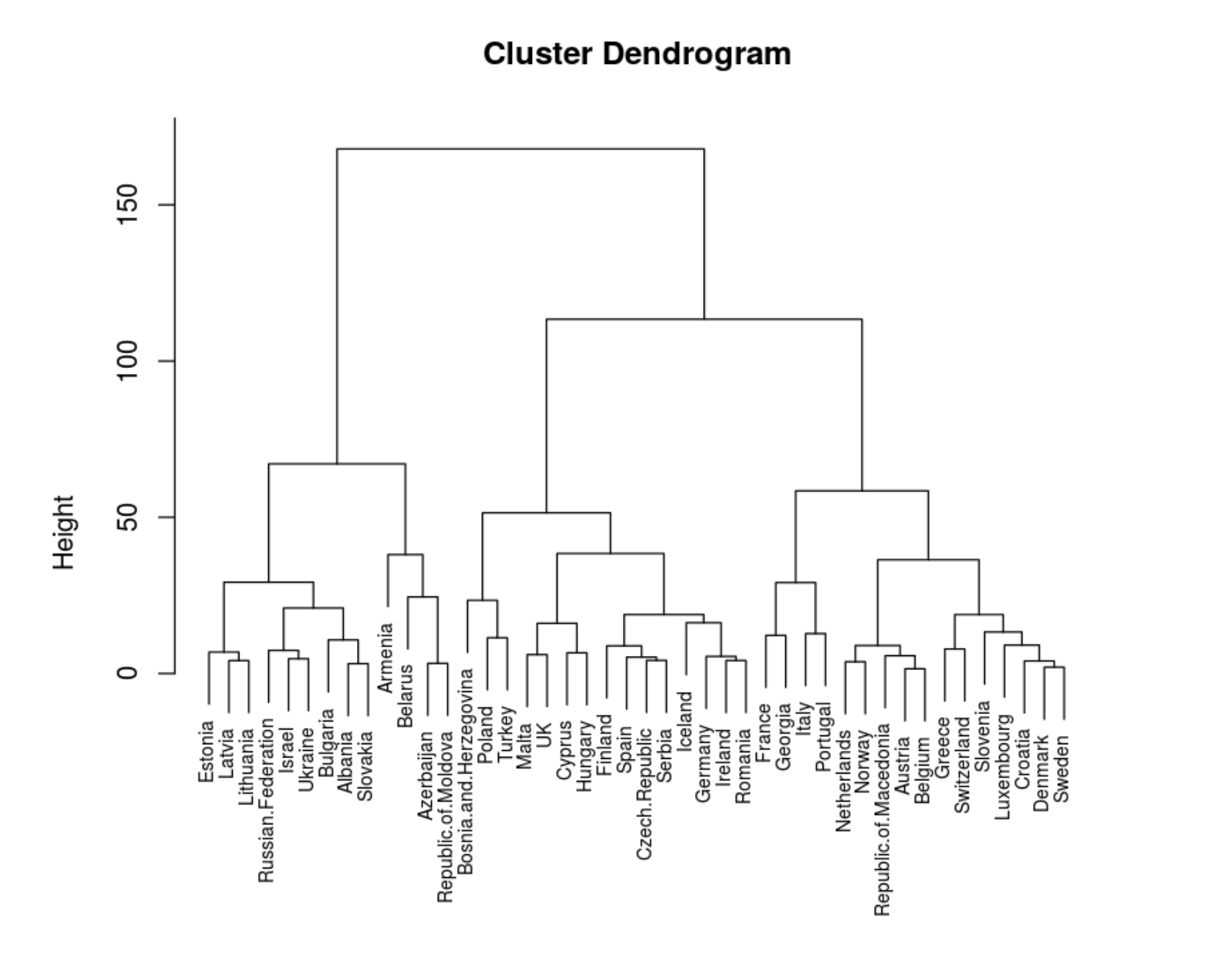
Нарисуем график поинтереснее. Цвета будут означать исходную географическую маркировку.
colors=c('green', 'red', 'blue')
hcd = as.dendrogram(hc)
clusMember = cutree(hc, 4)
colLab <- function(n) {
if (is.leaf(n)) {
a <- attributes(n)
labCol <- colors[data.group[n]]
attr(n, "nodePar") <- c(a$nodePar, lab.col = labCol)
}
n
}
clusDendro = dendrapply(hcd, colLab)
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
rect.hclust(hc, k = 4)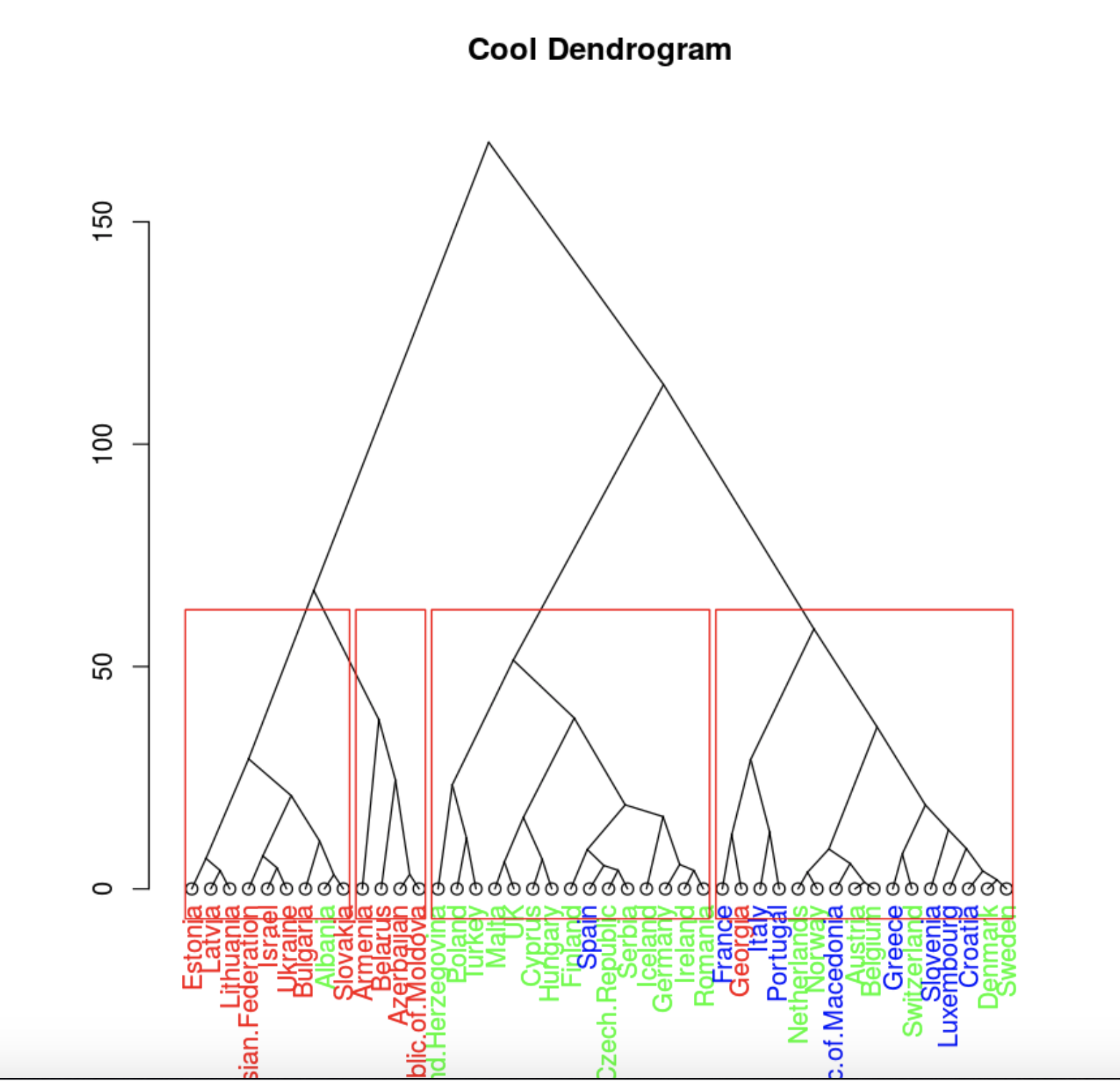
Грузия из восточного кластера единственная не попала в свой географический кластер. Пока отложим интерпретацию, посмотрим на другие методы.
Причем здесь, наверное, лучше использовать три кластера, так как в четвертый кластер странно выделились всего 4 страны.
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
data.hclas_group <- factor(cutree(hc, k = 3))
rect.hclust(hc, k = 3)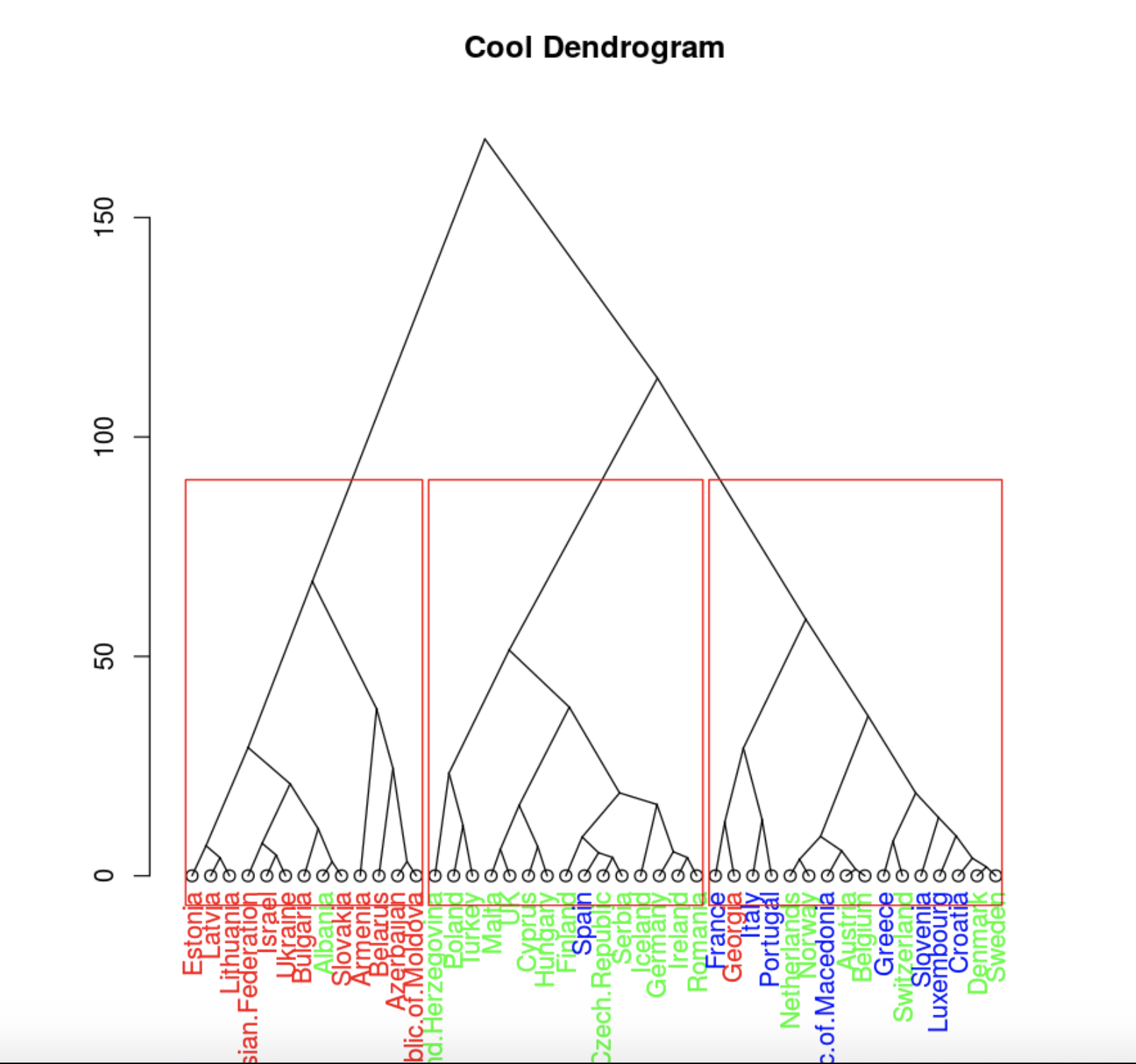
Конечно, если мы хотим увидеть информативный график в двух измерениях, нужно использовать первые две главные компоненты.
library(FactoMineR)
res.pca <- PCA(data,scale.unit=T, graph = F)
fviz_pca_biplot(res.pca,
col = colors[data.hclas_group], palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black",
legend.title = "groups4")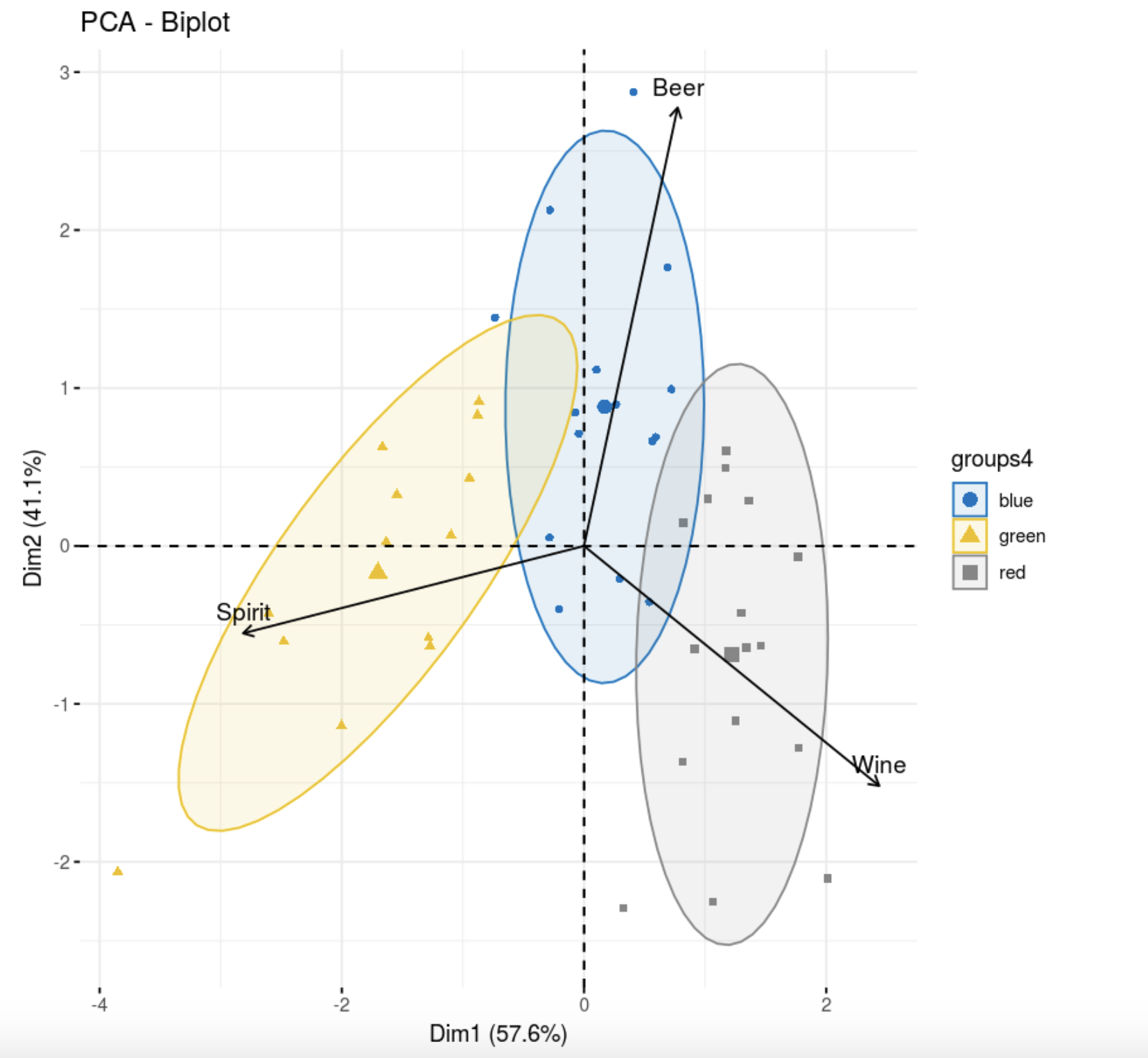
Третья группа, которая по центру, портит всю картину. Если бы она была покучнее, можно было говорить о кластеризации, а так это, скорее, сегментация. В целом, между группами заметно различие, посмотрим, как справится метод k-средних++.
library(flexclust)
data.kk <- kcca(data, k=3, family=kccaFamily("kmeans"),
control=list(initcent="kmeanspp"))
fviz_pca_biplot(res.pca,
col.ind =as.factor(data.kk@cluster), palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black", repel = TRUE,
legend.title = "clusters")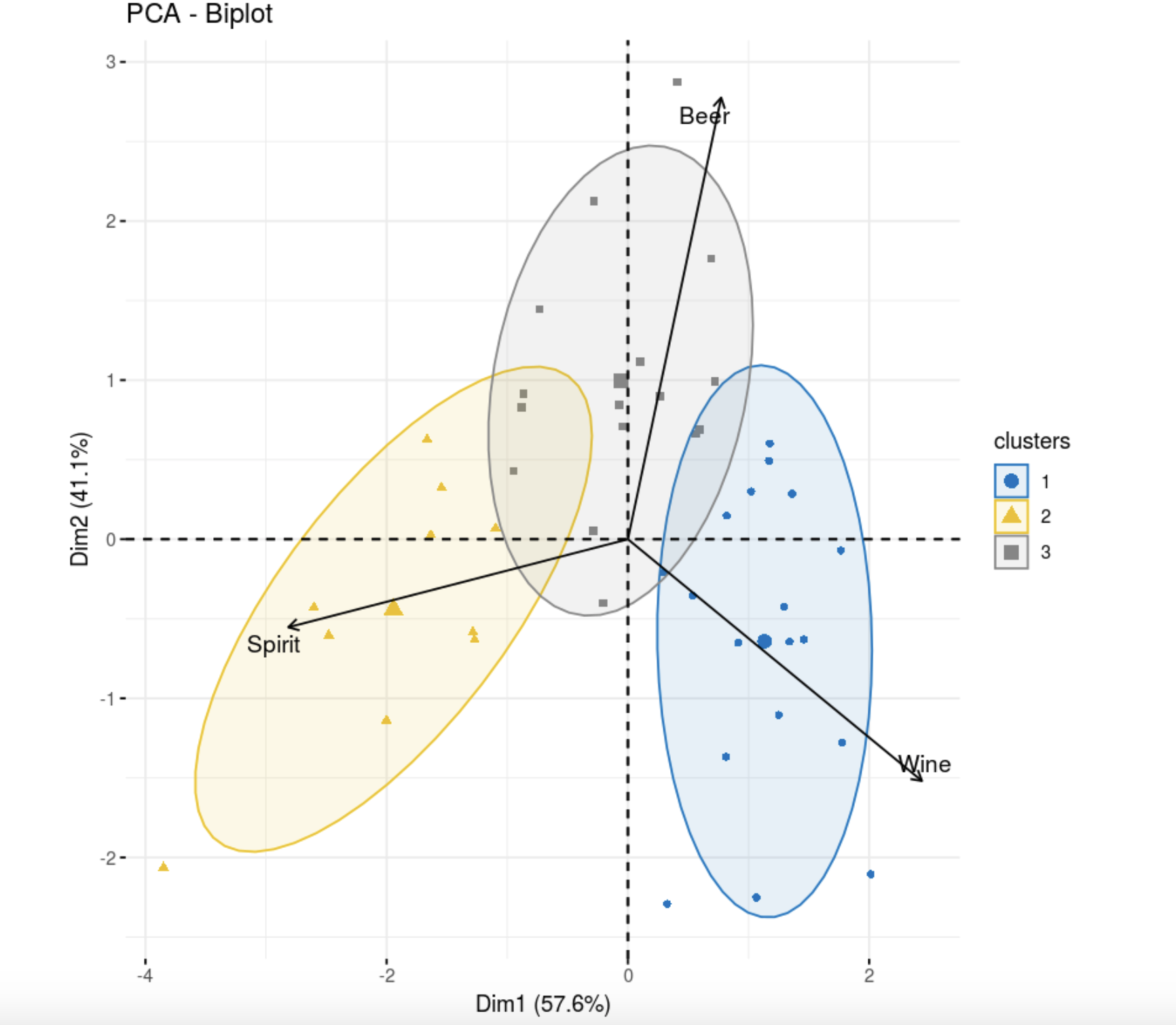
Эллипсоид третьей группы получился слишком широким, так как k-средних пытается разбить на равные кластеры. Из графика видно, что метод включил в третий кластер лишние точки, которые скорее должны относиться к другим кластерам.
Больше всего, исходя из исходных классов, на правду похож hclust. Проинтерпретируем результат.

Наиболее полный кластер, в смысле исходной классификации, образовали восточные страны. К ним попала Албания из центральной части. Стоит отметить, что Албания пространственно находится недалеко от восточных стран.
Второй кластер также очень похож на исходное разделение. В третьем же все плохо. В исходной выборке там меньше всего индивидов, и они очень близки по предпочтениям в алкоголе, согласно данным, к центральной части. Можно попробовать условно разделить на два кластера, так как видно, что для интерпретации лучше всего так и сделать и резюмировать биполярность Европы. Тогда кластера практически совпадут с Восточной и Западной Европой, где в Западную войдет центральная и Западная по исходным обозначениям.
Можно было бы провести кластеризацию на основе предположения о моделях кластеров, используя информационные критерии (тут описание), а также попробовать классический дискриминантный анализ для этого набора данных. Если эта статья была полезной, то планирую опубликовать продолжение.


drWhy
Ах, какое раздолье для анализа предпочтений на вполне конкретную душу населения наступит с введением индивидуальных штрих-кодов при продаже алкоголя!
Спасибо за статью.