

Собственно, задача — сделать все клетки поля «выключенными». Под катом кое-что интереснее, чем просто решение.
Сам алгоритм решения довольно нудный и объяснять его здесь долго. Вкратце — для поля каждого размера существует бинарная матрица A всех возможных ходов. Если представить изначальное поле в виде бинарного вектора X, то решение поля b — это решение системы бинарных линейных уравнений Ab = X. Нетрудно догадаться, что можно обратить матрицу A, сохранить её в переменной и находить решение уже любого поля по формуле b = A-1X. Если кто-то хочет почитать подробнее, то здесь есть потрясающая статья, описывающая все нюансы. Мы двигаемся дальше.
К слову, решение существует не всегда для любой размерности. Размеры 5x5 или 17x17, например, решение имеют не всегда и в этой статье мы их не рассматриваем.
Генерация паттернов
Рассмотрим для примера следующее поле 20x20:

А теперь давайте посмотрим на его решение:

Красиво, правда? Давайте увеличим размер (и выключим границы, а то от них рябит в глазах). Возьмём, например, 75x75:

И посмотрим на его решение:

Довольно красиво. Но давайте не мелочиться, а сразу возьмём 150x150:

И его решением будет… Ух ты.

Завораживает. Издалека похоже на план города. Или на древнегреческую мозаику. Или на туркменский ковёр. Только почему-то зелёный.
А что будет, если попробовать получить решение для решения? Получим ещё один узор, производный. А потом можно сделать так ещё раз и получить ещё один производный узор.



При этом рано или поздно узоры зацикливаются. Для разных размеров разные периоды, при этом для чётных полей период больше, чем для нечётных (6x6 и 7x7, на больших размерах период уже в несколько сотен минимум):


При этом любой производный узор сохраняет любую осевую отражательную симметрию (анимации не зациклены, в зацикленной версии должно быть 2045 кадров):



Помимо отражательной, производный паттерн также способен сохранять и вращательную симметрию:

Хэши
Помимо паттернов, Lights Out можно использовать как медленную, криптографически нестойкую (из-за детерминистичности), но экзотическую хэш-функцию.
Как именно её считать? Ну, например, если считать всё поле начальным значением, то можно использовать в качестве хэша первые два столбца второго производного поля. Главную задачу хэш-функции они сохраняют — при небольшом изменении в начальных данных хэш меняется заметно. Вот, посмотрите сами:

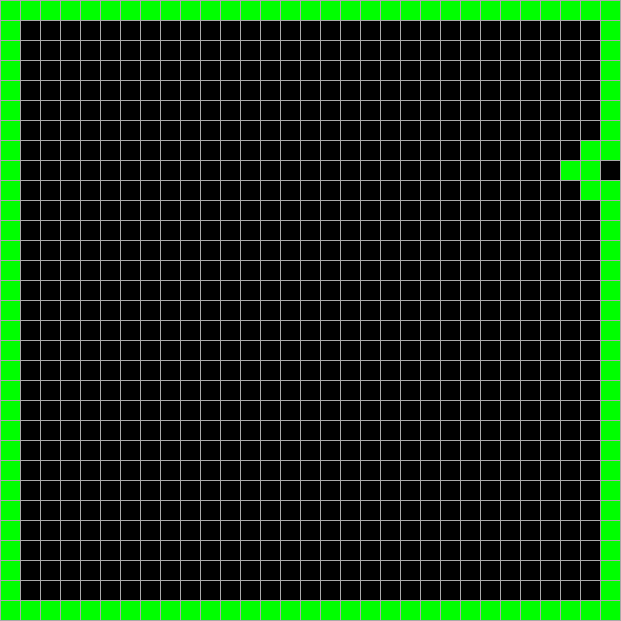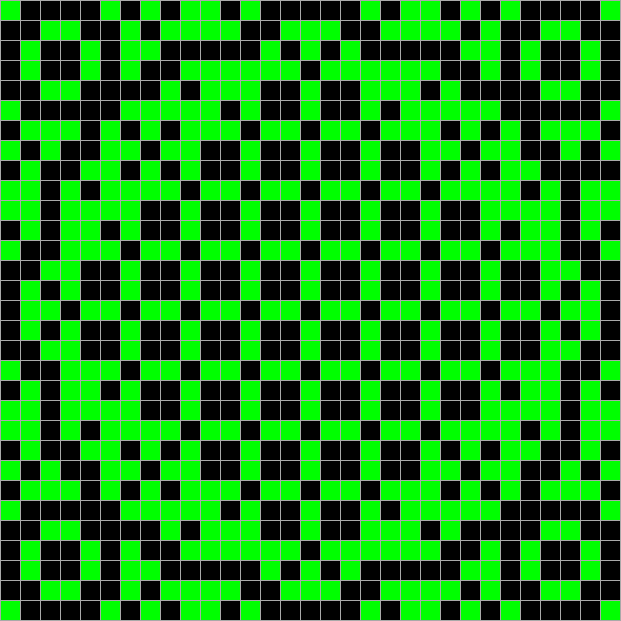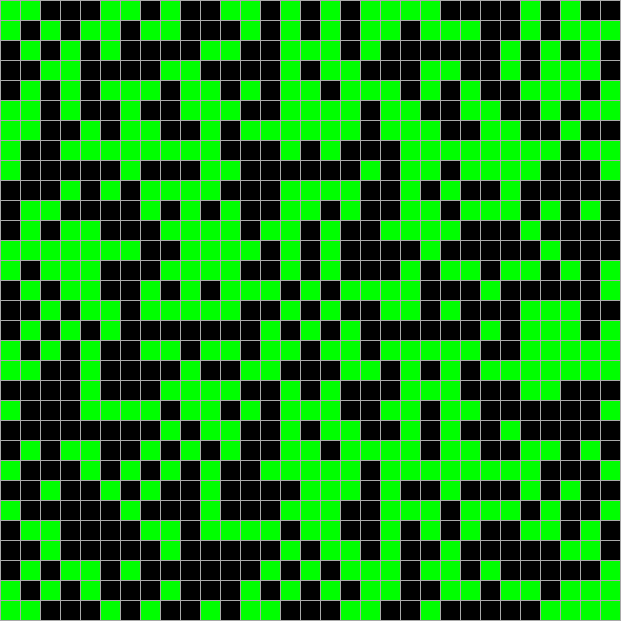
И только хэш:


Без анимации, чтобы заметить различие:


Где это можно применять? Ну, наверное, нигде. Для контрольных сумм он слишком медленный. В криптографии тоже не применить, потому что очень легко подобрать начальные данные, дающие данный хэш. Зато необычно.
Скрытие данных
Последнее применение — это скрытие данных внутри поля. Можно нарисовать на поле что-нибудь, затем несколько раз вычислить производный узор и выложить куда-нибудь. А благодаря цикличности изначально зашифрованное поле рано или поздно покажет себя. Вот пример (осторожно, гифка в 252 кадра). Если что, данные на 9-м кадре:

Приложение с исходниками на codeplex. К сожалению, пока есть версия только для Windows.
Комментарии (24)

Jeffry_Choser
10.04.2015 13:59Еще, было бы, любопытно взглянуть на алгоритм решения.

Sixshaman Автор
10.04.2015 14:40+3Да, собственно, ничего особенного. Поле предоставляется в виде 1-мерного бинарного вектора X длины n x n. Задача — получить те клетки поля, которые при ходе в них сделают его нулевым.
Далее, рассмотрим для примера поле 3x3. У нас есть изначальная конфигурация X и 9 возможных ходов.
Как можно записать ход в клетку (1, 1), например? Он выглядит так:

А как одномерный вектор он будет записан так:
[1]
[1]
[0]
[1]
[0]
[0]
[0]
[0]
[0]
Аналогично можно представить ходы во все остальные клетки. Обозначим их через a11...a33
Теперь о решении. Если, например, решением являются клетки (1, 2) и (3, 2), то математически решение запишется в виде:
a12 + a32 = X.
Более развёрнуто:
0*a11 + 1*a12 + 0*a13 + 0*a21 + 0*a22 + 0*a23 + 0*a31 + 1*a32 + 0*a33 = X.
Или в матричном виде:
[ a11 a12 a13 a21 a22 a23 a31 a32 a33]*b = X
Покороче:
Ab = X.
Наше искомое решение — это b. Решив эту систему бинарных линейных уравнений, мы получим вектор, состоящий из единиц и нулей. Если в эту клетку нужно сделать ход, то на её месте в векторе будет 1, если нет — то 0.
Для больших размерностей всё аналогично. Вот тут всё описывается на примере 5x5.
Ну и да, для некоторых размерностей у матрицы A ранг меньше, чем её размер, т.е. решение существует не всегда.
Jeffry_Choser
10.04.2015 21:55А как решая матрицу, получить координаты решения?
Или это итерационный процесс и из шага итерации получим конкретную клетку?
Sixshaman Автор
11.04.2015 00:09Ну, допустим, мы решили систему линейных уравнений и получили вектор b. Допустим, что у нас размер 3x3. Тогда
[ b11 ]
[ b12 ]
[ b13 ]
[ b21 ]
b = [ b22 ]
[ b23 ]
[ b31 ]
[ b32 ]
[ b33 ]
Ну вот, если bij = 1, то ход в клетку (i, j) содержится в решении. Если bij = 0, то нет.

Lerg
10.04.2015 14:18+1Красиво. Нужно сделать online реализацию на JavaScript.

Sixshaman Автор
10.04.2015 14:50Я думал об этом, кстати. Но руки так и не дошли. Зато непрерывную версию я писал уже на JS(всё равно без решалки, ни один человек из тех, что я спрашивал, не знает в принципе о возможности решения).

SHVV
10.04.2015 15:30+1Получился клёвый генератор ковров.
Только цвета добавить по кадрам и как-то смешивать их.
Jeffry_Choser
10.04.2015 21:57Цвет должен зависеть от кол-ва инверсий клетки. Клетка 2 раза зажглась — цвет поменялся и т.д.
NeoNN
10.04.2015 16:37А если сделать модицикацию, которая зажигает различные фигуры, как в тетрисе, в случайном порядке, то математически решение уже навряд ли можно будет найти и головоломка становится гораздо интереснее.

bromzh
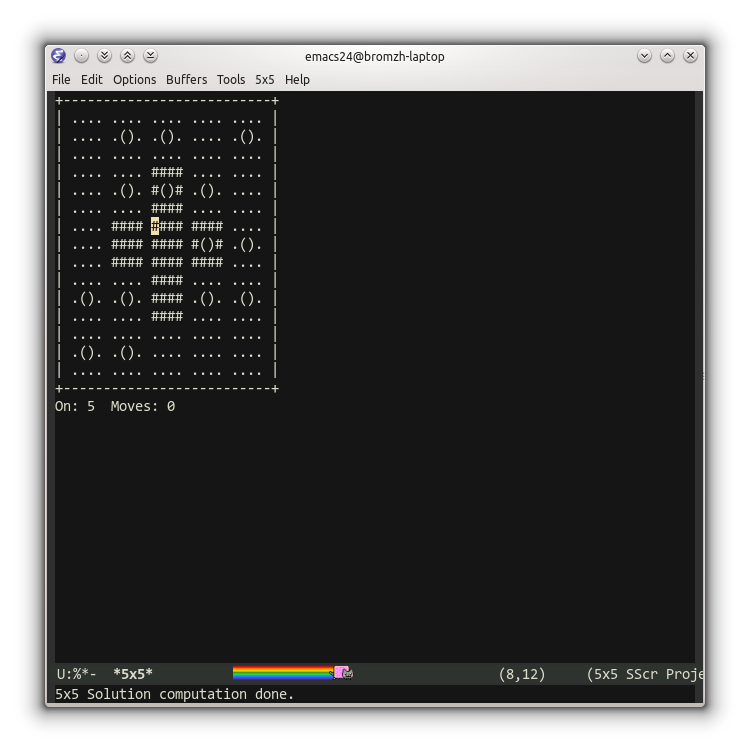
10.04.2015 18:12+2В емаксе есть эта игра, правда на ограниченном поле (M-x 5x5). И присутствует также возможность рассчитать решение:
СкринКружками отмечены поля, которые нужно активировать, чтобы выиграть

Mingun
10.04.2015 20:51Когда играл еще только в демку Myst IV, в камине был дощечка, на которой квадраты переключались таким образом. Уж не помню, сколько времени потратил, но таки смог «перекрасить ее».
Настоящее решение, если не играли, не читайтеИ так обидно было —на всякий случай :)такая изящная загадка была,ну все, это последний рубеж, пеняйте на себяа всего-то нужно было включить светильники…
dobriykot
10.04.2015 21:56Странно, что никто не вспомнил про это: i.imgur.com/ffH82gF.jpg

Jeffry_Choser
10.04.2015 21:58Колобки! :)

dobriykot
10.04.2015 22:01Да, это Братья Пилоты. :)
www.ag.ru/games/pilot-brothers-po-sledam-polosatogo-slona
Jeffry_Choser
10.04.2015 22:08У меня с детства комикс сохранился — приключения колобков, называется! :)

dtestyk
11.04.2015 10:57В криптографии тоже не применить, потому что очень легко подобрать начальные данные, дающие данный хэш
а если брать случайную матрицу А(случаи когда нет обратной можно использовать как одностороннюю функцию)


GarryC
Что то есть напоминающее Конвеевскую жизнь? НЕТ?
Sixshaman Автор
Да, есть такое. Только правила расчёта производного поля другие.
bask
И то и другое — клеточные автоматы
Jeffry_Choser
Или ожившие QR-коды :)