03.06.2020 11:13
avsmal 12 2800 Источник
Мы уже анонсировали читателям Хабра набор на магистерскую программу «Разработка программного обеспечения / Software Engineering» на базе Университета ИТМО. Первый этап вступительных испытаний на программу — онлайн тест. И для того, чтобы помочь нашим абитуриентам к нему подготовиться, мы решили опубликовать разбор нескольких математических задач из прошлогоднего варианта.


Задача 1

Решите в натуральных числах уравнение: $2^n + 1 = k^2$.

В ответе укажите максимально возможное значение произведения $k$ и $n$.

Давайте перенесём единицу в правую часть и применим формулу разности квадратов.

$2^n = k^2-1 = (k-1)(k+1).$


Степень двойки $2^n$ делится только на степени двойки. Поэтому нас интересуют такие $k$, при которых $(k-1)$ и $(k+1)$ одновременно являются степенями двойки. При $k=3$ получаем значения $2$ и $4$ соответственно. Значений больше быть не может, т.к. расстояние между степенями двойки возрастает. Таким образом, получаем $k = 3$ и $n = 3$. Ответ $k\cdot n = 9$.

Задача 2

Чему равен предел последовательности $(1 + \frac{1}{n})^{5n + 4}$?

В ответе укажите число. При необходимости оставьте три знака после запятой без округления.

Выделим замечательный предел:

$ \left(1 + \frac{1}{n}\right)^{5n + 4} = \left( \left(1 + \frac{1}{n}\right)^n \right)^5 \cdot \left(1 + \frac{1}{n}\right)^4. $


Предел первого множителя вычисляется по формуле замечательного предела:

$ \lim_{n\to\infty} \left( \left(1 + \frac{1}{n}\right)^n \right)^5 = e^5. $


Предел второго множителя очевиден:

$ \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^4 = 1. $


(Если нужно более формальное доказательство, то можно раскрыть скобки и заметить, что при $n\to\infty$ все слагаемые, кроме 1, стремятся к нулю.) Итак, оба предела существуют, следовательно

$ \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^{5n + 4} = \lim_{n\to\infty} \left( \left(1 + \frac{1}{n}\right)^n \right)^5 \cdot \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^4 = e^5 \cdot 1 \approx 148.413. $



Задача 3

Упростите сумму:

$1 - \frac{1}{4} + \frac{1}{3} - \frac{1}{16} + \frac{1}{9} -\frac{1}{64} + \frac{1}{27} - \dots - \frac{1}{4^n} + \frac{1}{3^n} + \dots $


В ответе укажите число. При необходимости оставьте три знака после запятой без округления.

Представим этот знакопеременный ряд как разность двух положительных последовательностей:

$ \begin{aligned} S_+ &= 1 + \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \dots \frac{1}{3^n} + \dots\\ S_- &= \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \dots + \frac{1}{4^n} \dots \end{aligned} $


По формуле суммы бесконечной убывающей геометрической последовательности получаем:

$S_+ = \frac{1}{1 - 1/3} = \frac32, \quad\quad S_- = \frac{1}{4}\cdot\frac{1}{1 - 1/4} = \frac13. $


Заметим, что $S_+ + S_- = \frac32 + \frac13 < \infty$, т.е. этот ряд является абсолютно сходящимся. Следовательно, мы можем вычислить его сумму, как разность $S_+$ и $S_-$:

$1 - \frac{1}{4} + \frac{1}{3} - \frac{1}{16} + \frac{1}{9} -\frac{1}{64} + \frac{1}{27} - \dots - \frac{1}{4^n} + \frac{1}{3^n} + \dots = S_+ - S_- = \frac{3}{2} - \frac{1}{3} = \frac{7}{6} \approx 1.166. $



Задача 4

Двадцать пять человек выбирают числа, каждый наугад выбирает число от $1$ до $100$ независимо друг от друга. Далее участники объявляют выбранные номера по очереди (и делают это честно). Первый (если такой человек есть), кто объявляет номер, который уже был объявлен, получает приз.

Какой человек по счету имеет наибольшую вероятность выиграть приз?

Оценим вероятность того, что $k$-ый человек получает приз: он получает приз в том случае, если предыдущие $k-1$ участников назвали различные числа, а он — одно из предыдущих $k-1$ чисел. Вероятность назвать одно из прозвучавших $k-1$ чисел равна

$p_k = \frac{k-1}{100}.$


Для участника с номером $i$ вероятность назвать число, которое ещё не прозвучало, равна

$q_i = \frac{100 - i + 1}{100}.$


Тогда искомая вероятность равна:

$ q_1 \cdot q_2\cdot\dotsb\cdot q_{k-1}\cdot p_k = \frac{100}{100}\cdot\frac{99}{100}\cdot\dotsb\cdot\frac{100- k + 2}{100}\cdot\frac{k-1}{100} = \frac{100!\cdot (k-1)}{(100 -k +1)!\cdot 100^k}. $


Осталось вычислить это значения для всех $k\in\{1,\dotsb,25\}$ и найти минимум. Это можно сделать небольшим скриптом, табличкой в Excel или через WolframAlpha:
{0, 0.01, 0.0198, 0.029106, 0.0376438, 0.0451725, 0.0514967, 0.0564747, 0.0600245, 0.0621254, 0.0628157, 0.0621875, 0.0603784, 0.0575607, 0.05393, 0.0496926, 0.0450547, 0.0402113, 0.0353386, 0.0305875, 0.0260799, 0.0219071, 0.0181307, 0.0147848, 0.0118793}

Отсюда получаем $k = 11$ (максимум достигается на одиннадцатом элементе списка $0.0628157$).

Задача 5

Каждый из девяти единичных квадратов $3\times 3$-квадрата случайным образом окрашен в красный или синий цвет с вероятностью $\frac{1}{2}$. Определите вероятность того, что ни один из четырёх квадратов $2\times2$ не является полностью красным.

В ответе укажите число. При необходимости оставьте три знака после запятой без округления.

В квадрате $3\times 3$ есть 4 различный квадрата $2\times 2$. Назовём их $A$, $B$, $C$ и $D$.



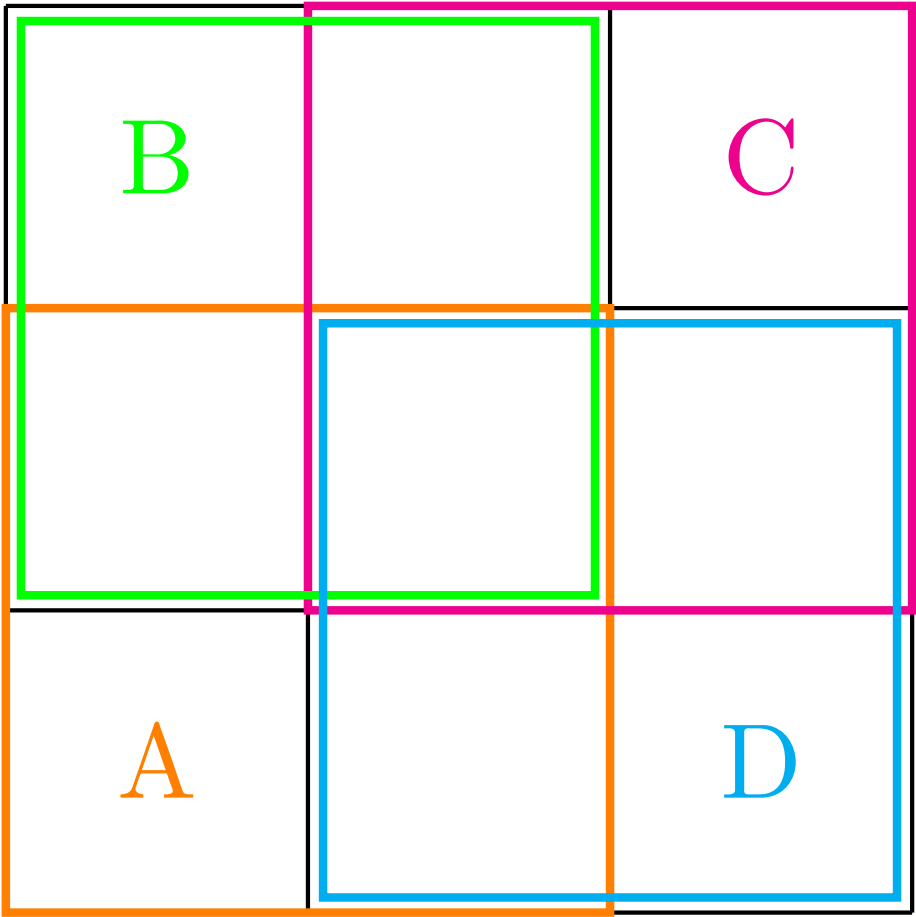
Обозначим этими же буквами события, что в соответствующем квадрате все ячейки окрашены красным. Тогда

$\Pr[A] = \Pr[B] = \Pr[C] = \Pr[D] = \frac{1}{2^4}.$



Для начала вычислим вероятность обратного события — вероятность того, что один из квадратов является полностью красным $\Pr[A\cup B\cup C\cup D]$. Для того, чтобы её вычислить, воспользуемся формулой включений-исключений:

$ \begin{aligned} \Pr[A\cup B\cup C\cup D] &= \Pr[A] + \Pr[B] + \Pr[C] + \Pr[D]\\ &- \Pr[A\cap B] - \Pr[A\cap C] - \Pr[A\cap D] - \Pr[B\cap C] - \Pr[B\cap D] - \Pr[C\cap D]\\ & + \Pr[A\cap B\cap C] + \Pr[A\cap B\cap D] + \Pr[A\cap C\cap D] + \Pr[B\cap C\cap D]\\ &- \Pr[A\cap B\cap C\cap D]\\ &= 4\cdot \frac{1}{2^4} - 4 \cdot \frac{1}{2^6} - 2 \cdot \frac{1}{2^7} + 4 \cdot \frac{1}{2^8} - \frac{1}{2^9}\\ &= \frac{1}{2^2} - \frac{1}{2^4} - \frac{1}{2^6} + \frac{1}{2^6} - \frac{1}{2^9}\\ &= \frac{1}{4} - \frac{1}{16} - \frac{1}{512} = \frac{128 - 32 - 1}{512} = \frac{95}{512}. \end{aligned} $


Искомая вероятность, что ни один из четырёх квадратов $2\times2$ не является полностью красным, равна

$1 - \Pr[A\cup B\cup C\cup D] = 1 - \frac{95}{512} = \frac{417}{512}\approx 0.814.$



Задача 6

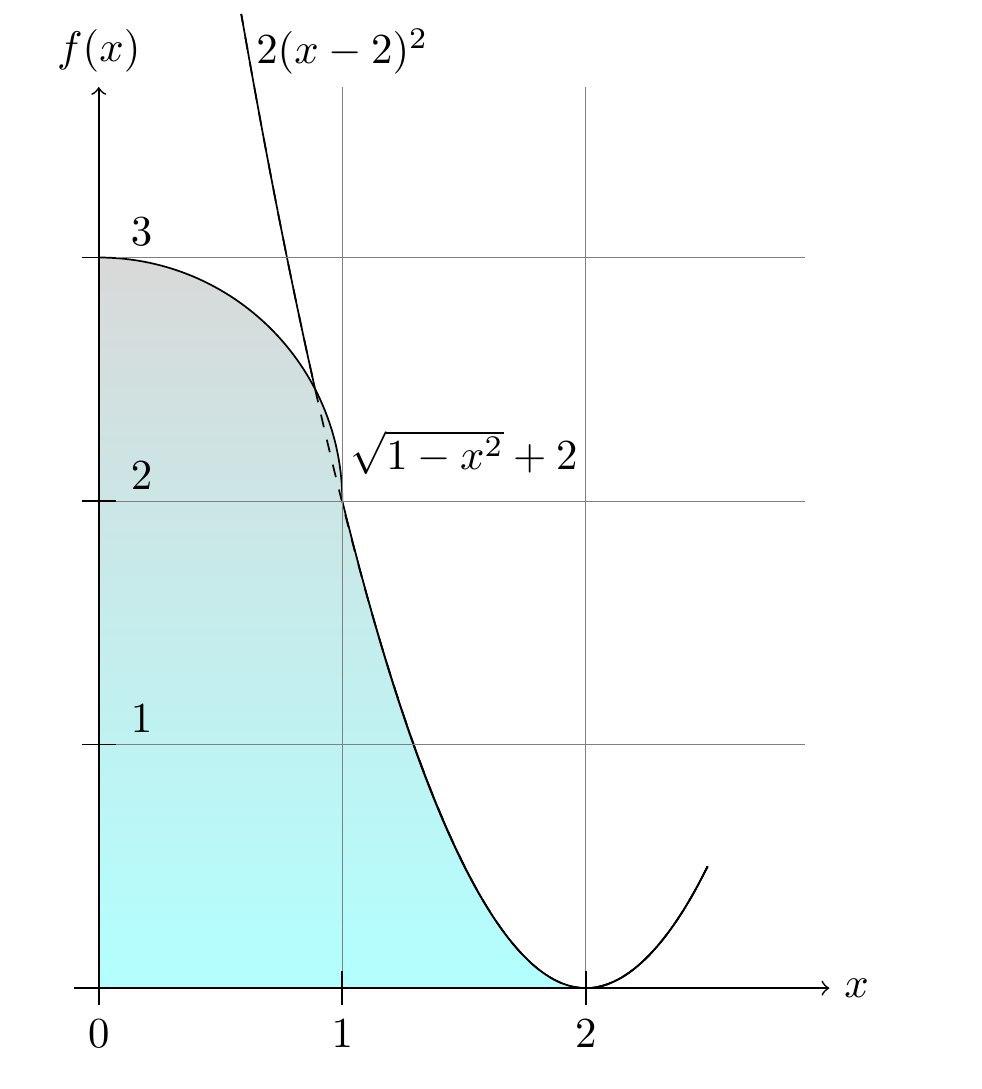
Вычислите объём фигуры вращения, образованной выделенной областью при вращении относительно вертикальной оси.


В ответе укажите число. При необходимости оставьте три знака после запятой без округления.

В нашем случае задача упрощается тем, что верхняя часть фигуры вращения — это половинка шара радиуса 1. Поэтому объём верхней части можно выписать сразу — он равен $2\pi/3$ (объём сферы вычисляется по формуле $4\pi R^3/3$).

Осталось разобраться с нижней частью, ограниченной параболой $y = 2(x-2)^2$. Объём фигуры вращения можно вычислить, если разбить объём на цилиндры маленькой высоты. Объём цилиндра равен произведению площади основания ($\pi R^2$) на высоту. Соответственно, нам нужно получить зависимость радиуса (роль радиуса играет $x$) от высоты (от $y$).

$ y = 2(x-2)^2 \implies x = 2 \pm \sqrt{y/2}. $


На интересует случай $x\le 2$, поэтому $x = 2 - \sqrt{y/2}$. Объём нижней части фигуры можно выразить следующим интегралом:

$ \begin{aligned} \int\limits_0^2\pi (2 - \sqrt{y/2})^2\, dy &= \pi\int\limits_0^2\left(4 - 4\sqrt{y/2} + y/2\right)dy\\ &=\pi\left.\left(4y - \frac{4}{\sqrt{2}}\cdot \frac{2}{3}\cdot y^{3/2} + \frac{y^2}{2\cdot2}\right)\right\rvert_0^2\\ &=\pi\left(4\cdot 2 - \frac{4\sqrt{2}}{3}\cdot{2^{3/2}} + 1\right) = \pi(9 - 16/3) = 11\pi/3. \end{aligned} $


Итого, в сумме получаем $2\pi/3 + 11\pi/3 = 13\pi/3\approx 13.613$.

Заключение


Надеемся, что этот разбор поможет абитуриентам подготовиться к онлайн- тесту.
В этом году он состоит из 12 задач, на которые мы выделяем 2 часа. Стоит учесть, что помимо математических, в нём есть и задачи на программирование. Весь процесс поступления и подробности о следующих этапах описаны на сайте магистерской программы. Если у вас остались вопросы, кураторы с радостью ответят на них по почте или в телеграм канале.