Вступительное испытание на корпоративную магистерскую программу JetBrains на базе Университете ИТМО начинается с онлайн-теста. Летом мы опубликовали разбор нескольких математических задач из теста 2019 года, а сегодня представляем разбор одного из вариантов прошедшего набора.
Несколько слов о том, как устроен тест. Абитуриенты получают ссылку на закрытый курс на платформе Stepik.org. Далее у них есть несколько недель на то, чтобы приступить к решению. Тест состоит из 12 задач, на них отводится два часа. Решать задачи можно в произвольном порядке, за каждую из них начисляется один балл. Проходной балл меняется от года к году. В этот раз он был довольно низким — задачи получились сложные. Кураторы программы сделали выводы и постараются к следующему набору подготовить задачи полегче.
Когда в задаче спрашивается про касательную к графику функции, то это почти всегда связанно с вычислением производной. В данном случае требуется найти производную для неявно заданной функции. Будем считать, что — это функция от . Продифференциируем обе части равенства по . Получаем Это позволяет выразить производную через и .
Теперь можно вычислить значение производной в точке . Обозначим это значение . Это значение задаёт тангенс угла наклона касательной к кривой в точке . Осталось вспомнить, что уравнение прямой можно задать в виде . Зная, что прямая должна проходить через точку , мы можем вычислить : Следовательно, . Получаем, что уравнение искомой прямой имеет вид: Приводим его к требуемой форме домножив на 21 и получаем:
Это задача на программирование, но с некоторой математической составляющей. Чтобы вычислить площадь искомой области, можно вычислить площадь под графиками функций и на отрезке между точками пересечения и вычесть одну из другой. Можно поступить проще: сразу рассматривать функцию и вычислить площадь под графиком этой функции между её корнями. Это немного упростит задачу. Предлагается следующий алгоритм:
Далее идёт реализация этого алгоритма на Питоне
Заметим, что вектора , и — ортогональны (это можно проверить вычислив попарные скалярные произведения), но не нормированы. Давайте найдём проекцию на каждый из трёх векторов.
Таким образом
Осталось выразить
В ответе нужно записать сумму координат . Можно было бы сначала вычислить , а потом сложить его координаты, но можно ещё проще: воспользуемся тем, что сумма координат суммы векторов, равна сумме сумм координат каждого из слагаемых.
Для получения ответа, вычислим суммы координат для каждого из векторов отдельно и сложим их с соответствующими коэффициентами:
По определению можно вывести явную формулу: (тут мы используем показательную форму записи комплексного числа, это соответствует ). Подставляем это в уравнение и получаем:
Остаётся решить уравнение на показатели. Тут нужно помнить, что . Поэтому, получаем уравнение
Домножаем на и делим на . Получается следующее уравнение в целых числах, где нас интересует решение с минимальным положительным целым .
Проверив , находим ответ при .
Это задача на перевод числа из одной системы счисления. Если нам дано число в системе счисления с основанием , то его значение можно вычислить, как
Это же можно вычислить по схеме Горнера:
Для того, чтоб перевести в число в системе счисления по основанию , нужно повторить эту процедуру в обратном порядке. Тогда цифра будет вычисляться по формуле
Ниже представлена реализация этой идеи на Питоне.
Задача на комбинаторику и теорию графов. Рассмотрим одного студента. Он сам дружит не более, чем с тремя студентами. Каждый его друг имеет не более 2 других друзей. Других студентов по условию быть не может. Получаем, что всего не более студентов. Осталось проверить, что такую граф существует, но это несложно сделать на листочке.
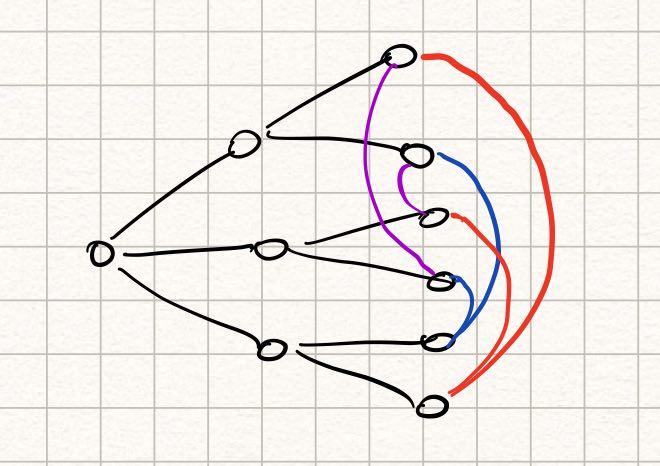
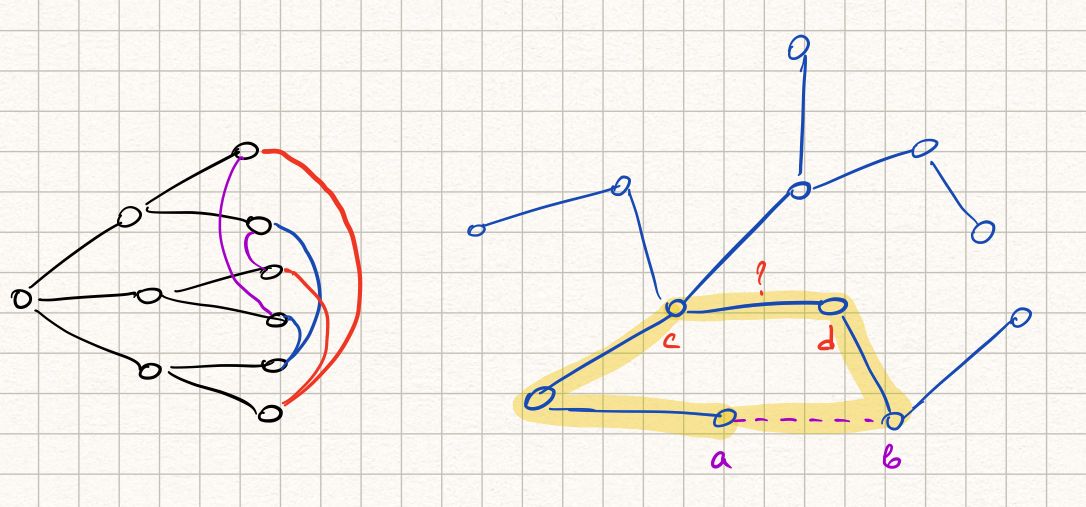
Левая вершина — рассматриваемый студент, правее три его друга и шесть друзей друзей. Цвета рёбер значения не имеют и нужны только для понятности картинки.
Это простая задачка на три цикла — числа небольшие, результат можно быстро посчитать короткой программой.
Но писать программу необязательно, ответ не так сложно вычислить аналитически (на тесте такого требования не было). Для этого заметим, что исходная задача эквивалентна следующей.
Это уже типовая задача. Нам нужно разбить последовательность предметов на 4 части. Для этого нужно вставить перегородки. По формуле для разбиения получаем
Это задача на вычисление длины кривой. Длина кривой вычисляется через определённый интеграл
В нашем случае, , . Для вычисления , точки пересечения с осью абсцисс, нужно подставить : получаем . Вычислим :
Вычисляем интеграл:
Это чисто программистская задача на использование массивов, словарей и сортировок. Ниже представлено решение этой задачи на Питоне с комментариями.
Задача на теорию графов. Тут нужно показать, что какую бы стратегию мы не выбрали, нам придётся перебрать все пары компьютеров, т.е. задать вопросов. До этого нетрудно догадаться, и для ответа на тест этого достаточно. Тем не менее, давайте постараемся разобраться, почему это так.
Довольно легко придумать следующую простую идею, которая всё объясняет: если мы про какую-то пару компьютеров не спросили, например, не спросим про пару , то давайте рассмотрим сеть, в которой компьютер соединён только с компьютером . Если не спросить про , то мы не можем быть уверены, что соединён хоть к каким-то компьютером. Это рассуждение объясняет, почему нужно спросить про все пары компьютеров, и приводит к правильному ответу. Только вот это рассуждение не является корректным. Проблема заключается в том, что мы неявно предполагаем, что наши вопросы не зависят от ответов на предыдущие вопросы. Когда мы предлагаем рассмотреть сеть, в которой компьютер соединён только с компьютером , то это уже другая сеть, нежели та, на которой мы не спросили про пару . На разных сетях вопросы могут быть устроены по-разному. Другими словами, это рассуждение позволяет доказать, что не существует пары компьютеров , про которую мы не спросим ни для какой конфигурации сети. При этом, если для каждой конфигурации сети существует какая-то пара, про которую мы не спрашиваем, то это не противоречит нашему рассуждению.
Корректное объяснение может выглядеть, например, так. Предположим, что вместо честного ответа на вопросы об устройстве сети, нам отвечают таким образом, чтобы заставить нас задавать как можно больше вопросов (такое доказательство называется рассуждением о противнике (adversary argument)). Как ему это сделать? Можно придерживаться следующей стратегии: отвечать «Да» только в том случае, если ответ «Нет» будет означать, что сеть несвязна. Давайте покажем, что при такой стратегии ответов нам всегда придётся спросить про все пары компьютеров. Рассмотрим граф, в котором вершины соответствуют компьютерам, а рёбра — тем парам, для которых мы получили ответ «Да». Заметим, что при такой стратегии ответов на вопросы получившийся граф будет ациклическим. Действительно, если в какой-то момент в графе появился цикл, то это означает, что мы получили ответ «Да» на вопрос про некоторую пару , про которую можно было ответить «Нет», ведь уже связаны другими рёбрами, т.е. ответ «Нет» на вопрос о не означает несвязность сети. Теперь предположим, что мы убедились в связности сети не спросив про все пары. Это значит, что полученный граф представляет собой дерево содержащее все 32 вершины. Пусть — пара компьютеров, про которую мы не спросили. Давайте добавим ребро к дереву. Так как в дереве уже были пути между всеми парами вершин, то новое ребро добавит цикл.

Рассмотрим этот цикл и выберем на нём ребро, про которое мы спрашивали последним. Пусть это ребро . Спрашивая про пару мы получили ответ «Да». По нашей стратегии нам отвечают «Да» только, если ответ «Нет» означал бы несвязность графа. Но это противоречит тому, что про пару мы ничего не спрашивали: можно было бы ответить «Нет» на вопрос о и всё равно добиться связности графа за счёт ответа «Да» на вопрос об . Это противоречит предположению о выбранной стратегии ответов на вопросы.
Это задача на теорию вероятностей и формулу Байеса. Обозначим следующие события: — у Вани грипп, — у Вани ветрянка.
Пусть — это наличие сыпи. Известно, что
Нас просят оценить условную вероятность . По теореме Байеса:
Вероятность выпадения сыпи можно вычислить по формуле полной вероятности:
В результате получаем:
Надеемся, что этот разбор поможет абитуриентам программы подготовиться к онлайн-тесту. Для самостоятельной проверки предлагаем прорешать второй вариант. Все материалы вступительных испытаний опубликованы на сайте программы. Там же вы сможете найти полное описание процесса поступления. Не забывайте, что за успешным прохождением онлайн-теста следует устный этап вступительного испытания.
P.S. Внимательный читатель заметит, что в разборе 11 задач, а в тесте их должно быть 12. Одна из задач оказалась технически сложной, и мы решили её не разбирать, чтобы никого не пугать.

Несколько слов о том, как устроен тест. Абитуриенты получают ссылку на закрытый курс на платформе Stepik.org. Далее у них есть несколько недель на то, чтобы приступить к решению. Тест состоит из 12 задач, на них отводится два часа. Решать задачи можно в произвольном порядке, за каждую из них начисляется один балл. Проходной балл меняется от года к году. В этот раз он был довольно низким — задачи получились сложные. Кураторы программы сделали выводы и постараются к следующему набору подготовить задачи полегче.
Задача 1
Найдите уравнение касательной к кривой в точке . Ответ запишите в виде , где — целые несократимые числа и (без пробелов и скобок), например, .
Когда в задаче спрашивается про касательную к графику функции, то это почти всегда связанно с вычислением производной. В данном случае требуется найти производную для неявно заданной функции. Будем считать, что — это функция от . Продифференциируем обе части равенства по . Получаем Это позволяет выразить производную через и .
Теперь можно вычислить значение производной в точке . Обозначим это значение . Это значение задаёт тангенс угла наклона касательной к кривой в точке . Осталось вспомнить, что уравнение прямой можно задать в виде . Зная, что прямая должна проходить через точку , мы можем вычислить : Следовательно, . Получаем, что уравнение искомой прямой имеет вид: Приводим его к требуемой форме домножив на 21 и получаем:
Задача 2
На плоскости нарисованы две кривые, заданные многочленами второй степени.
Найдите площадь замкнутой области, которая ограничена этими кривыми. Если такой области нет, то нужно вывести число 0.
Вход
На первой строке три целых числа , , , задающие первую кривую , на второй строке — три целых числа , и , задающие кривую . Все числа по модулю не превосходят .
Выход
Площадь замкнутой области, ограниченная и .
Ответ должен быть вычислен с точностью 5 знаков после запятой.
Это задача на программирование, но с некоторой математической составляющей. Чтобы вычислить площадь искомой области, можно вычислить площадь под графиками функций и на отрезке между точками пересечения и вычесть одну из другой. Можно поступить проще: сразу рассматривать функцию и вычислить площадь под графиком этой функции между её корнями. Это немного упростит задачу. Предлагается следующий алгоритм:
- вычисляем коэффициенты ,
- проверяем, что получился квадратный многочлен (), и что он имеет два различных корня (дискриминант больше нуля), если нет — возвращаем ноль,
- вычисляем корни и ,
- вычисляем площадь под графиком между и ,
- возвращаем модуль этого значения, т.к. при интеграл будет отрицательным.
Далее идёт реализация этого алгоритма на Питоне
# считываем коэффициенты f(x) и g(x)
a1, b1, c1 = map(int, raw_input().split())
a2, b2, c2 = map(int, raw_input().split())
# вычисляем коэффициенты h(x)
a = a1 - a2
b = b1 - b2
c = c1 - c2
# проверяем наличие корней
d = b * b - 4 * a * c
if a == 0 or d <= 0:
print(0)
exit(0)
# вычисляем корни
r1 = (-b - math.sqrt(d)) / (2.0 * a)
r2 = (-b + math.sqrt(d)) / (2.0 * a)
# первообразная для h(x)
def H(x):
return a*x*x*x/3.0 + b*x*x/2.0 + c*x
# вычисляем определённый интеграл и выводим его модуль в требуемом формате
print("{:.5f}".format(math.fabs(H(r2) - H(r1))))
Задача 3
В пространстве задано стандартное скалярное произведение, — подпространство, заданное как линейная оболочка векторов , , . Найти ортогональную проекцию вектора на подпространство вектор и ортогональную составляющую этого же вектора ().
В ответ напишите сумму координат вектора (например, для вектора сумма координат будет 9).
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Заметим, что вектора , и — ортогональны (это можно проверить вычислив попарные скалярные произведения), но не нормированы. Давайте найдём проекцию на каждый из трёх векторов.
Таким образом
Осталось выразить
В ответе нужно записать сумму координат . Можно было бы сначала вычислить , а потом сложить его координаты, но можно ещё проще: воспользуемся тем, что сумма координат суммы векторов, равна сумме сумм координат каждого из слагаемых.
Для получения ответа, вычислим суммы координат для каждого из векторов отдельно и сложим их с соответствующими коэффициентами:
Задача 4
Обозначим за — комлексный корень степени из единицы с минимальным положительным аргументом (аргумент = угол в полярной форме комплексного числа). Например, .
Найдите минимальное положительное целое , являющееся решением следующего уравнения.
По определению можно вывести явную формулу: (тут мы используем показательную форму записи комплексного числа, это соответствует ). Подставляем это в уравнение и получаем:
Остаётся решить уравнение на показатели. Тут нужно помнить, что . Поэтому, получаем уравнение
Домножаем на и делим на . Получается следующее уравнение в целых числах, где нас интересует решение с минимальным положительным целым .
Проверив , находим ответ при .
Задача 5
Маленькому мальчику Ване на кружке по системам счисления задали следующую задачу: перевести число в системе счисления в систему счисления . Недолго думая, он позвал на помощь своего лучшего друга Петю, который славился тем, что замечательно умел считать до на пальцах. После нескольких бессонных ночей ребята общими усилиями справились с задачей.
Однако, на следующем занятии Ване задали похожую задачу, где , к сожалению, превышало . Тогда ребята решили обратиться к старшей сестре Пети с просьбой написать универсальную программу, которая решает задачу для любых , и . Ваша цель – выполнить просьбу Вани и Пети.
Входные данные
Во входных данных вашей программе дается три числа: исходное число , основания систем счисления и (). Число в десятичной системе счисления не превышает .
Выходные данные
В выходных данных должно быть число , записанное в системе счисления , или , если входные данные некорректны (число во входных данных не является корректной записью числа в системе счисления ).
Это задача на перевод числа из одной системы счисления. Если нам дано число в системе счисления с основанием , то его значение можно вычислить, как
Это же можно вычислить по схеме Горнера:
Для того, чтоб перевести в число в системе счисления по основанию , нужно повторить эту процедуру в обратном порядке. Тогда цифра будет вычисляться по формуле
Ниже представлена реализация этой идеи на Питоне.
# считываем входные данные
xstr, b, c = raw_input().split()
s1 = int(b)
s2 = int(c)
# проверяем входные данные и преобразуем в число
x = 0
for c in xstr:
if int(c) >= s1:
print(-1)
exit()
x = x * s1 + int(c)
# переводим в заданную систему счисления
res = ""
if x == 0:
res = "0"
else:
while x > 0:
res = str(x % s2) + res
x = x // s2
print(res)
Задача 6
Про студентов магистерской программы Software Engineering известно, что они дружат друг с другом так, что каждый студент дружит не более чем с 3 другими, и для любых двух студентов верно, что они либо дружат друг с другом, либо есть студент, который дружит с ними обоими.
Какое максимальное число студентов на магистерской программе Software Engineering?
Задача на комбинаторику и теорию графов. Рассмотрим одного студента. Он сам дружит не более, чем с тремя студентами. Каждый его друг имеет не более 2 других друзей. Других студентов по условию быть не может. Получаем, что всего не более студентов. Осталось проверить, что такую граф существует, но это несложно сделать на листочке.

Левая вершина — рассматриваемый студент, правее три его друга и шесть друзей друзей. Цвета рёбер значения не имеют и нужны только для понятности картинки.
Задача 7
Сколько различных решений имеет следующее уравнение
если известно, что , , , ?
Это простая задачка на три цикла — числа небольшие, результат можно быстро посчитать короткой программой.
count = 0
for x1 in range(1,51):
for x2 in range(2,51):
for x3 in range(51):
if x1 + x2 + x3 <= 50:
count = count + 1
print(count)
Но писать программу необязательно, ответ не так сложно вычислить аналитически (на тесте такого требования не было). Для этого заметим, что исходная задача эквивалентна следующей.
Сколько различных решений имеет следующее уравнение(Мы вычли из правой части и добились того, чтобы все переменные начинались с нуля.)
если известно, что ?
Это уже типовая задача. Нам нужно разбить последовательность предметов на 4 части. Для этого нужно вставить перегородки. По формуле для разбиения получаем
Задача 8
Найти длину кривой , заключённой в первой четверти.
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Это задача на вычисление длины кривой. Длина кривой вычисляется через определённый интеграл
В нашем случае, , . Для вычисления , точки пересечения с осью абсцисс, нужно подставить : получаем . Вычислим :
Вычисляем интеграл:
Задача 9
На вход программе подаётся строка, содержащая слова, разделённые пробелом. Слово – это последовательность латинских символов, окружённая пробелами или границами строк.
Для всех слов, которые встречаются в тексте более одного раза, программа должна вычислить минимальное количество слов между повторениями.
Вход
Строка, содержащая последовательность строчных латинских символов, разделённых пробелами.
Выход
Выведите все слова, которые встречаются более одного раза, и минимальное количество слов между их повторениями, в формате
слово: число
Выведите эту информацию в том порядке, в котором слова встречаются в тексте в первый раз.
Это чисто программистская задача на использование массивов, словарей и сортировок. Ниже представлено решение этой задачи на Питоне с комментариями.
# считываем входную строку и разбиваем на слова
words = raw_input().split()
# заводим необходимые словари
idx = {} # хранит номер последнего вхождения слова
dist = {} # хранит минимальное расстояние между повторениями
first = {} # хранит номер первого вхождения
# проходим по словам и вычисляем минимальное расстояние для каждого слова
for i in range(len(words)):
if words[i] in idx:
if dist[words[i]] > i - idx[words[i]] - 1:
dist[words[i]] = i - idx[words[i]] - 1
else:
first[words[i]] = i
dist[words[i]] = 2 * len(words) # замена +бесконечности
idx[words[i]] = i
# массив для хранения слов, которые встречаются более одного раза
good = []
for k in dist:
if dist[k] < len(words):
good.append((k, dist[k], first[k]))
# упорядочиваем массив по номеру первого вхождения
good.sort(key=lambda t: t[2])
# выводим результат
for t in good:
print("{}: {}".format(t[0], t[1]))
Задача 10
В студенческом общежитии ИТМО очень сложно устроена локальная сеть — местный администратор не любит роутеры, потому сетевые кабели протянуты напрямую между некоторыми компьютерами (для этого в некоторые компьютеры пришлось установить дополнительные сетевые карты).
Вам, как новичку в общежитии, хочется выяснить как все устроено. Поэтому вы можете выбрать любые два компьютера и получить ответ на вопрос “проложен ли между ними провод?”. Вам бы хотелось узнать — можно ли в общежитии передать информацию с любого компьютера до любого другого по проводам.
Какое минимальное количество вопросов необходимо задать чтобы гарантированно получить ответ, если всего в общежитии установлено 32 компьютера?
Задача на теорию графов. Тут нужно показать, что какую бы стратегию мы не выбрали, нам придётся перебрать все пары компьютеров, т.е. задать вопросов. До этого нетрудно догадаться, и для ответа на тест этого достаточно. Тем не менее, давайте постараемся разобраться, почему это так.
Довольно легко придумать следующую простую идею, которая всё объясняет: если мы про какую-то пару компьютеров не спросили, например, не спросим про пару , то давайте рассмотрим сеть, в которой компьютер соединён только с компьютером . Если не спросить про , то мы не можем быть уверены, что соединён хоть к каким-то компьютером. Это рассуждение объясняет, почему нужно спросить про все пары компьютеров, и приводит к правильному ответу. Только вот это рассуждение не является корректным. Проблема заключается в том, что мы неявно предполагаем, что наши вопросы не зависят от ответов на предыдущие вопросы. Когда мы предлагаем рассмотреть сеть, в которой компьютер соединён только с компьютером , то это уже другая сеть, нежели та, на которой мы не спросили про пару . На разных сетях вопросы могут быть устроены по-разному. Другими словами, это рассуждение позволяет доказать, что не существует пары компьютеров , про которую мы не спросим ни для какой конфигурации сети. При этом, если для каждой конфигурации сети существует какая-то пара, про которую мы не спрашиваем, то это не противоречит нашему рассуждению.
Корректное объяснение может выглядеть, например, так. Предположим, что вместо честного ответа на вопросы об устройстве сети, нам отвечают таким образом, чтобы заставить нас задавать как можно больше вопросов (такое доказательство называется рассуждением о противнике (adversary argument)). Как ему это сделать? Можно придерживаться следующей стратегии: отвечать «Да» только в том случае, если ответ «Нет» будет означать, что сеть несвязна. Давайте покажем, что при такой стратегии ответов нам всегда придётся спросить про все пары компьютеров. Рассмотрим граф, в котором вершины соответствуют компьютерам, а рёбра — тем парам, для которых мы получили ответ «Да». Заметим, что при такой стратегии ответов на вопросы получившийся граф будет ациклическим. Действительно, если в какой-то момент в графе появился цикл, то это означает, что мы получили ответ «Да» на вопрос про некоторую пару , про которую можно было ответить «Нет», ведь уже связаны другими рёбрами, т.е. ответ «Нет» на вопрос о не означает несвязность сети. Теперь предположим, что мы убедились в связности сети не спросив про все пары. Это значит, что полученный граф представляет собой дерево содержащее все 32 вершины. Пусть — пара компьютеров, про которую мы не спросили. Давайте добавим ребро к дереву. Так как в дереве уже были пути между всеми парами вершин, то новое ребро добавит цикл.

Рассмотрим этот цикл и выберем на нём ребро, про которое мы спрашивали последним. Пусть это ребро . Спрашивая про пару мы получили ответ «Да». По нашей стратегии нам отвечают «Да» только, если ответ «Нет» означал бы несвязность графа. Но это противоречит тому, что про пару мы ничего не спрашивали: можно было бы ответить «Нет» на вопрос о и всё равно добиться связности графа за счёт ответа «Да» на вопрос об . Это противоречит предположению о выбранной стратегии ответов на вопросы.
Задача 11
Школьник Ваня приболел, и его мама решила вызвать врача домой. У врача есть статистика по району, где живет Ваня. У больных детей этого района — грипп, у остальных — ветрянка. Других болезней в этом районе не зафиксировано.
Один из основных симптомов ветрянки – это сыпь, она появляется в случаях заболевания ветрянкой. Однако, во время гриппа она тоже возможна и появляется в случаях.
Осмотрев Ваню, врач обнаружил сыпь. Какова вероятность того, что у Вани ветрянка?
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Это задача на теорию вероятностей и формулу Байеса. Обозначим следующие события: — у Вани грипп, — у Вани ветрянка.
Пусть — это наличие сыпи. Известно, что
Нас просят оценить условную вероятность . По теореме Байеса:
Вероятность выпадения сыпи можно вычислить по формуле полной вероятности:
В результате получаем:
Заключение
Надеемся, что этот разбор поможет абитуриентам программы подготовиться к онлайн-тесту. Для самостоятельной проверки предлагаем прорешать второй вариант. Все материалы вступительных испытаний опубликованы на сайте программы. Там же вы сможете найти полное описание процесса поступления. Не забывайте, что за успешным прохождением онлайн-теста следует устный этап вступительного испытания.
P.S. Внимательный читатель заметит, что в разборе 11 задач, а в тесте их должно быть 12. Одна из задач оказалась технически сложной, и мы решили её не разбирать, чтобы никого не пугать.



dmtrka
Задачи то на самом деле очень лёгкие. Они вряд-ли даже за пределы первого курса выходят. Внимание вопрос: А не будут ли в магистратуре 2 года просто изучать то что уже прошли на 2,3 и 4 курсах?
avsmal Автор
Программа обучения открыта, так что судите сами. Там действительно встречаются курсы, которые по программе могут пересекаться с тем, что изучается в бакалавриате, но обычно это компенсируется глубиной изложения. Т.е. название курса такое же, но курс более продвинутый и глубокий.
atomic1989
Только все забывается)