07.06.2020 13:56
lightln2 104 23700 Источник
image

Сложно найти человека, не знакомого с игрой "Жизнь", придуманной английским математиком Джоном Конвеем еще в 1970 году, и до сих пор не теряющей своей популярности. Многие программисты писали свою реализацию этой игры, и еще одна вряд ли кого-то удивит. Однако эта игра является отличным примером, показывающим, насколько полезной может оказаться оптимизация вычислений, даже не меняющая асимтотическую сложность алгоритма. Мы начнем с простейшей реализации на c# и будем последовательно применять различные оптимизации, ускоряя работу программы.

Мы также улучшим алгоритм на JavaScript, ускорив его в 10 раз по сравнению с неоптимизированной версией.

В конце статьи дана ссылка на код, а также на online-реализацию игры с оптимизированным алгоритмом на JavaScript, выполняющим до двухсот итераций в секунду на поле размера 1920x1080 (Full HD), где вы можете убить время поиграть в эту замечательную игру.

Правила игры


Игра «Жизнь» идет на плоскости, состоящей из клеток, каждая клетка имеет 8 соседей. Клетки могут быть «живые» или «мертвые». В каждой итерации (еще называемой «поколением») состояние поля меняется в зависимости от количества живых соседей: если рядом с живой клеткой два или три живых соседа, клетка выживает в следующем поколении. Если рядом с мертвой клеткой ровно три живых соседа, то в следующем поколении клетка «рождается».

Например:

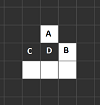— клетка A имеет одного живого соседа, поэтому она умирает;
— клетка B имеет трех живых соседей, поэтому она остается жить;
— клетка C имеет трех живых соседей, поэтому она рождается;
— клетка D имеет пять живых соседей, поэтому она остается мертвой.

Код на c# требует .NET Core 3.1. За исключением одного класса (использующего System.Runtime.Intrinsics.X86), остальной код должен работать .NET Framework и на более ранних версиях .NET Core. Разработка велась в Visual Studio Community Edition 2019.

Реализация на JavaScript не требует никаких зависимостей, хотя игру желательно запускать в браузере Chrome, поскольку в Microsoft Edge он работает крайне медленно. Разработка велась в Visual Studio Code.

Как устроен код на c#


Размер игрового поля зафиксирован как 1920x1080 (Full HD), причем крайние клетки всегда мертвые. Это не влияет на производительность, но упрощает алгоритмы, избавляя от проверок на граничные условия. Все алгоритмы наследуются от абстрактного класса LifeJourney, что позволяет унифицировать их тестирование:

LifeJourney.cs 
public abstract class LifeJourney 
{
    public const int WIDTH = 1920;
    public const int HEIGHT = 1080;
    public string Name => GetType().Name;
    public abstract void Set(int i, int j, bool value);
    public abstract bool Get(int i, int j);
    public abstract void Step(); // makes one iteration. Performance-critical!
    public void Clear() 
    {
        for (int i = 1; i < WIDTH - 1; i++)
            for (int j = 1; j < HEIGHT - 1; j++)
                Set(i, j, false);
    }
    public void GenerateRandomField(int seedForRandom, double threshold) { ... }
    ... // other methods
}


Юнит-тесты запускают один и тот же набор тестов для каждого алгоритма:

LifeTesting.cs 
public class LifeTesting 
{
       public static void PerformAllTests(LifeJourney life) 
       {
            TestGetSet(life);
            TestSetSimpleFigure(life);
            TestSimpleFigureAtStart(life);
            TestSimpleFigureAtSecondPos(life);
            TestSimpleFigure(life);
            TestGenerate(life);
            TestRandomField(life);
        }
        ...
        private static void TestRandomField(LifeJourney life) 
        {
            life.GenerateRandomField(12345, 0.5);
            life.Step();
            Assert.AreEqual(565797, life.GetLiveCellsCount());
            Assert.AreEqual(-717568334, life.GetFingerprint());
        }
    }

   [TestClass]
    public class TestDifferentLives 
    {
        [TestMethod]
        public void Test_1_SimpleLife() => 
            LifeTesting.PerformAllTests(new SimpleLife());
        ...
    }


Тестирование производительности создает поле случайной заливкой с использованием генератора случайных чисел с фиксированным seed-ом (так что каждый раз поле получается одним и тем же). После этого запускается цикл из тысячи итераций, и в конце замеряется время (в секундах), а также проверяется конечное состояние поля (количество выживших клеток и хеш-код) для дополнительной проверки корректности работы алгоритма:

RunPerformanceTest 
public abstract class LifeJourney 
{
    public void GenerateRandomField(int seed, double threshold)
    {
        Random rand = new Random(seed);
        for (int i = 1; i < WIDTH - 1; i++)
            for (int j = 1; j < HEIGHT - 1; j++)
            {
                Set(i, j, rand.NextDouble() < threshold);
            }
    }

    public void RunPerformanceTest(int steps) 
    {
        GenerateRandomField(12345, 0.5);
        Stopwatch timer = new Stopwatch();
        timer.Start();
        Run(steps);
        double elapsedSeconds = timer.Elapsed.TotalSeconds;
        Console.WriteLine($"{Name} Performance: {(steps / elapsedSeconds):0.000} steps/sec");
    }
    ... // other methods
}

class Program
{
    static void Main(string[] args)
    {
        int steps = 1000;
        new SimpleLife().RunPerformanceTest(steps);
        ...
    }
}


1. Наивная реализация


Начнем с самой простой реализации: поле представлено массивом boolean, хранящим информацию о живых клетках; каждая итерация выполняется в два прохода:

  1. для каждой клетки считаем количество ее соседей и записываем будущее состоянее клетки в отдельный массив temp;
  2. копируем массив temp в исходный массив.

Два прохода нужны потому, что состояние клетки на следующем шаге зависит от состояния ее соседей на текущем шаге, поэтому мы не можем менять состояние клеток, пока мы не вычислили весь следующий шаг.

SimpleLife 
public class SimpleLife : LifeJourney
{
    bool[,] field = new bool[WIDTH, HEIGHT];
    bool[,] temp = new bool[WIDTH, HEIGHT];

    public override bool Get(int i, int j) => field[i, j];

    public override void Set(int i, int j, bool value) => field[i, j] = value;

    public override void Step()
    {
        for (int i = 1; i < WIDTH - 1; i++)
        {
            for (int j = 1; j < HEIGHT - 1; j++)
            {  // первый проход: вычисляем будущее состоянее
                bool isAlive = field[i, j];
                int numNeigbours = 0;
                if (field[i - 1, j - 1]) numNeigbours++;
                if (field[i - 1, j]) numNeigbours++;
                if (field[i - 1, j + 1]) numNeigbours++;
                if (field[i, j - 1]) numNeigbours++;
                if (field[i, j + 1]) numNeigbours++;
                if (field[i + 1, j - 1]) numNeigbours++;
                if (field[i + 1, j]) numNeigbours++;
                if (field[i + 1, j + 1]) numNeigbours++;
                bool keepAlive = isAlive && (numNeigbours == 2 || numNeigbours == 3);
                bool makeNewLive = !isAlive && numNeigbours == 3;
                temp[i, j] = keepAlive | makeNewLive;
            }
        }

        for (int i = 1; i < WIDTH - 1; i++)
            for (int j = 1; j < HEIGHT - 1; j++)
                // второй проход: копируем вычисленное состояние в текущее
                field[i, j] = temp[i, j];
            }
        }
    }
}


Результат работы:

Алгоритм: SimpleLife
Время работы: 40 секунд
Скорость работы: 25 шагов в секунду

Исходный код: SimpleLife.cs

2. Добавляем байты


В предыдущем алгоритме для каждой клетки выполняется 8 операций сравнения. Попробуем уменьшить их число:

— Вместо двумерного массива boolean создадим одномерный массив байт, в котором живая клетка представлена значением 1, а мертвая — 0.

— Вместо восьми проверок будем суммировать байты соседей текущей клетки, тогда их сумма и будет равна числу живых соседей.

— Во временный массив будем писать сумму клеток, отложив проверку на второй проход:

LifeBytes 
public class LifeBytes : LifeJourney
{
    byte[] field = new byte[WIDTH * HEIGHT];
    byte[] temp = new byte[WIDTH * HEIGHT];
    public override bool Get(int i, int j) => field[j * WIDTH + i] == 1;
    public override void Set(int i, int j, bool value) => field[j * WIDTH + i] = (byte)(value ? 1 : 0);

    public override void Step()
    {
        for (int i = 1; i < WIDTH - 1; i++)
            for (int j = 1; j < HEIGHT - 1; j++)
            {  // считаем число соседей для текущей клетки и кладем в temp[pos]
                int pos = j * WIDTH + i;
                temp[pos] = (byte)(
                    field[pos - WIDTH - 1] + field[pos - WIDTH] + field[pos - WIDTH + 1] +
                    field[pos - 1] + field[pos + 1] +
                    field[pos + WIDTH - 1] + field[pos + WIDTH] + field[pos + WIDTH + 1]);
            }

        for (int i = 1; i < WIDTH; i++)
            for (int j = 1; j < HEIGHT; j++)
            {  // обновляем текущее состояние
                // по числу соседей и прошлому состоянию клетки
                int pos = j * WIDTH + i;
                bool keepAlive = field[pos] == 1 && (temp[pos] == 2 || temp[pos] == 3);
                bool makeNewLife = field[pos] == 0 && temp[pos] == 3;
                field[pos] = (byte)(makeNewLife | keepAlive ? 1 : 0);
            }
    }
}


Проверяем:

Алгоритм: LifeBytes
Время работы: 25 секунд
Скорость работы: 40 шагов в секунду
Ускорение от предыдущей версии: 1.6
Ускорение от первой версии: 1.6

Исходный код: LifeBytes.cs

3. Добавляем восьмибайтные слова


Заметим, что при первом проходе для всех байт выполняются одни и те же восемь сложений, что
наводит на мысль вместо обработки одного байта сразу обрабатывать 8 байтов, так как для многих инструкций, работающих с байтом, на современных процессорах есть аналогичные инструкции, работающие с двух-, четырех- и восьмибайтными словами. В нашем случае сложение восьмибайитных слов будет давать такой же результат, что и восемь сложений соседних байт подряд:

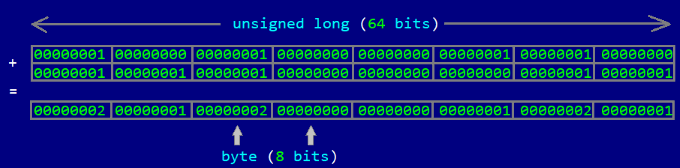
image

Заметим, что это не всегда верно, так как если при арифметических операциях с байтами происходит переполнение, то аналогичные операции с длинными словами будут давать неправильный результат. Однако нам повезло, и максимальное значение, которое мы можем получить при сложении в байте, равно восьми, и переполнение у нас случиться не может.
Чтобы заменить операции над байтами операциями над восьмибайтными словами, нам надо воспользоваться доступной в c# арифметикой указателей:

— пометить класс как unsafe;
— получить указатели на оба массива;
— преобразовывать указатель на байт в указатель на ulong

вот так 
fixed (byte* fieldPtr = field, tempPtr = temp)
{
    for (int i = WIDTH + 1; i < WIDTH * HEIGHT - WIDTH - 1; i += 8)
    {
        ulong* ptr = (ulong*)(tempPtr + i);
        *ptr += *(ulong*)(fieldPtr + i - WIDTH - 1);
        *ptr += *(ulong*)(fieldPtr + i - WIDTH);
        *ptr += *(ulong*)(fieldPtr + i - WIDTH + 1);
        *ptr += *(ulong*)(fieldPtr + i - 1);
        *ptr += *(ulong*)(fieldPtr + i + 1);
        *ptr += *(ulong*)(fieldPtr + i + WIDTH - 1);
        *ptr += *(ulong*)(fieldPtr + i + WIDTH);
        *ptr += *(ulong*)(fieldPtr + i + WIDTH + 1);
    }
    ...
}


Меряем производительность, и…

Алгоритм: LongLife
Время работы: 10 секунд
Скорость работы: 100 шагов в секунду
Ускорение от предыдущей версии: 2.5
Ускорение от первой версии: 4

Исходный код: LongLife.cs

4. Добавляем поиск в таблице


Мы неплохо оптимизировали первый проход, однако во втором проходе на каждый байт выполняются несколько проверок, от чего мы хотим избавиться. Стандартная оптимизация в таких случаях — lookup table, когда результат для всех комбинаций входных данных вычисляется заранее и кладется в таблицу. Наши входные данные — текущее состояние клетки (один байт в оригинальном массиве) и количество соседей (один байт во временном массиве). Мы могли бы вычислить таблицу для всех комбинаций этих байт, что нам даст размер таблицы 16 килобайт, однако мы можем сократить размер таблицы, заодно упростив код. Идея состоит в том, что количество соседей от 0 до 8 не занимает целый байт, а умещается в младшие три бита (на самом деле, в четыре, но 8 соседей и 0 соседей дают одинаковый эффект, поэтому мы игнорируем четвертый бит в количестве соседей). Поэтому мы закодируем состояние текущей клетки в четвертом бите этого же байта, и наша таблица будет длиной 16 байт, из которых только три значения равны единице. Значения, равные единице, соответствуют индексам, кодирующим мертвую клетку с тремя соседами или живую клетку с двумя или тремя соседями:

image

Сам код получается не сильно сложнее 
public unsafe class LifeIsLookingUp : LifeJourney
{
    static byte[] alivePerNeighbours = new byte[256];
    byte[] field = new byte[WIDTH * HEIGHT];
    byte[] temp = new byte[WIDTH * HEIGHT];

    public LifeIsLookingUp()
    {
        alivePerNeighbours[3] = 1;
        alivePerNeighbours[8 + 2] = 1;
        alivePerNeighbours[8 + 3] = 1;
    }
    ...
    public override void Step()
    {
        fixed (byte* fieldPtr = field, tempPtr = temp)
        {
            ...

            // второй прогон использует таблицу!
            for (int i = WIDTH; i < WIDTH * HEIGHT - WIDTH; i++)
            {
                byte neighbours = (byte)((tempPtr[i] & 7) | (fieldPtr[i] << 3));
                fieldPtr[i] = alivePerNeighbours[neighbours];
            }
            ...
    }
}


В итоге получаем ускорение почти в два раза:

Алгоритм: LifeIsLookingUp
Время работы: 5.5 секунд
Скорость работы: 180 шагов в секунду
Ускорение от предыдущей версии: 1.8
Ускорение от первой версии: 7.2

Исходный код: LifeIsLookingUp.cs

5. Добавляем битовую магию


На этот раз забудем предыдущую оптимизацию и заново оптимизируем второй шаг, чтобы не только избавиться от условных выражений, но, как и в первом шаге, вычислять по восемь клеток за раз. Нам надо, фактически, придумать битовую функцию, которая будет получать те же самые результаты, что и lookup table из предыдущего шага. Те, кто изучал булевую алгебру, знают, что для любой таблицы истинности (а наша lookup table именно ей и является) можно написать соответствующую булеву функцию, хотя она и может получиться сложной. Однако существует метод диаграммы Карно, позволяющий из таблицы истинности получить сильно оптимизированную булеву функцию простым и наглядным способом. Этот метод отлично применим и к нашей таблице; однако, учитывая, что в ней всего 16 входных значений, при некотором везении опыте можно подобрать нужную функцию перебором.
Опустим промежуточные выкладки и приведем:

получившийся код 
for (int i = WIDTH; i < WIDTH * HEIGHT - WIDTH; i ++)
{
    byte neighbours = tempPtr[i];
    byte alive = fieldPtr[i];
    neighbours &= (byte)0b00000111;
    byte aliveAndNeighbours = ((neighbours & ~(byte)0b00000001) >> 1) | (alive << 2);
    aliveAndNeighbours ^= (byte)~0b00000101;
    aliveAndNeighbours &= (aliveAndNeighbours >> 2);
    aliveAndNeighbours &= (aliveAndNeighbours >> 1);
    aliveAndNeighbours &= (byte)0b00000001;

    ulong makeNewLife = neighbours | (alive << 3);
    makeNewLife ^= (byte)~0b00000011;
    makeNewLife &= (makeNewLife >> 2);
    makeNewLife &= (makeNewLife >> 1);
    makeNewLife &= (byte)0b00000001;
     
    fieldPtr[i] = aliveAndNeighbours | makeNewLife;
}


В данном виде этот код не особо лучше поиска по таблице, поскольку делает слишком много операций на байт. Однако он позволяет перейти от побайтовых вычислений к обработке 8 байтов за раз:

Аналогичный код для ulong вместо байт 
for (int i = WIDTH; i < WIDTH * HEIGHT - WIDTH; i += 8)
{
    ulong neighbours = *(ulong*)(tempPtr + i);
    ulong alive = *(ulong*)(fieldPtr + i);
    neighbours &= 0b00000111_00000111_00000111_00000111_00000111_00000111_00000111_00000111ul;

    ulong aliveAndNeighbours = ((neighbours & ~0b00000001_00000001_00000001_00000001_00000001_00000001_00000001_00000001ul) >> 1) | (alive << 2);
    aliveAndNeighbours ^= ~0b00000101_00000101_00000101_00000101_00000101_00000101_00000101_00000101ul;
    aliveAndNeighbours &= (aliveAndNeighbours >> 2);
    aliveAndNeighbours &= (aliveAndNeighbours >> 1);
    aliveAndNeighbours &= 0b00000001_00000001_00000001_00000001_00000001_00000001_00000001_00000001ul;

    ulong makeNewLife = neighbours | (alive << 3);
    makeNewLife ^= ~0b00000011_00000011_00000011_00000011_00000011_00000011_00000011_00000011ul;
    makeNewLife &= (makeNewLife >> 2);
    makeNewLife &= (makeNewLife >> 1);
    makeNewLife &= 0b00000001_00000001_00000001_00000001_00000001_00000001_00000001_00000001ul;

    *(ulong*)(fieldPtr + i) = aliveAndNeighbours | makeNewLife;
}


Код стал совершенно непонятным, однако работает почти в два раза быстрее предыдущей версии:

Алгоритм: LifeInBits
Время работы: 3.3 секунды
Скорость работы: 300 шагов в секунду
Ускорение от предыдущей версии: 1.7
Ускорение от первой версии: 12

Исходный код: LifeInBits.cs

6. Храним по две клетки на байт


Последняя оптимизация такого типа логично вытекает из предыдущих: до сих пор мы хранили по одной клетке на байт, обрабатывая по восемь байтов за один раз, но во всех вычислениях мы на самом деле оперировали только четырьмя младшими битами в байте, так как старшие четыре бита всегда были нули. Теперь мы будем хранить по две клетки на один байт: одну в младших четырех битах, другую — в старших. Временный массив, хранящий число соседей, также будет хранить количество соседей независимо в младших и в старших четырех битах. Выгода в том, что мы все равно будем обрабатывать по восемь байт за раз, но в этот раз в них будет не восемь, а уже шестнадцать клеток! Потенциально это может привести к более чем двукратному ускорению, так как, кроме уменьшения в два раза количества операций, мы также уменьшаем в два раза размер используемой памяти, что позволит лучше утилизировать кеш процессора.
В самом алгоритме при втором прогоне меняются только константы и границы итерирования, но при первом прогоне из-за упаковки по две клетки в байт приходится приходится применять логические сдвиги на 4 и 60 бит влево и вправо, что делает код более запутанным:

Две клетки в байте 
public override void Step()
{  
    fixed (byte* fieldPtr = field, tempPtr = temp)
    {  // прежде всего обнуляем временный массив
        for (int i = 0; i < temp.Length; i += 8)  *(ulong*)(tempPtr + i) = 0;
        // теперь вместо сдвига указателей применяются арифметические сдвиги
        for (int i = WIDTH; i < WIDTH * HEIGHT / 2; i += 8)
        {
            ulong* ptr = (ulong*)(tempPtr + i);

            ulong src1 = *(ulong*)(fieldPtr + i - WIDTH / 2);
            ulong src2 = *(ulong*)(fieldPtr + i);
            ulong src3 = *(ulong*)(fieldPtr + i + WIDTH / 2);

            ulong src4 = *(ulong*)(fieldPtr + i - WIDTH / 2 - 8);
            ulong src5 = *(ulong*)(fieldPtr + i - 8);
            ulong src6 = *(ulong*)(fieldPtr + i + WIDTH / 2 - 8);

            ulong src7 = *(ulong*)(fieldPtr + i - WIDTH / 2 + 8);
            ulong src8 = *(ulong*)(fieldPtr + i + 8);
            ulong src9 = *(ulong*)(fieldPtr + i + WIDTH / 2 + 8);

            *ptr += (src1 << 4) + src1 + (src1 >> 4);
            *ptr += (src2 << 4) + (src2 >> 4);
            *ptr += (src3 << 4) + src3 + (src3 >> 4);

            *ptr += (src4 >> 60) + (src5 >> 60) + (src6 >> 60);
            *ptr += (src7 << 60) + (src8 << 60) + (src9 << 60);
        }
        // здесь поменялись только константы
        for (int i = WIDTH; i < WIDTH * HEIGHT / 2; i += 8)
        {
            ulong neighbours = *(ulong*)(tempPtr + i);
            ulong alive = *(ulong*)(fieldPtr + i);
            neighbours &= 0b0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111_0111ul;

            ulong keepAlive = ((neighbours & ~0b0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001ul) >> 1) | (alive << 2);
            keepAlive ^= ~0b0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101_0101ul;
            keepAlive &= (keepAlive >> 2);
            keepAlive &= (keepAlive >> 1);
            keepAlive &= 0b0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001ul;

            ulong makeNewLife = neighbours | (alive << 3);
            makeNewLife ^= ~0b0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011_0011ul;
            makeNewLife &= (makeNewLife >> 2);
            makeNewLife &= (makeNewLife >> 1);
            makeNewLife &= 0b0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001ul;

            *(ulong*)(fieldPtr + i) = keepAlive | makeNewLife;
        }

    }
    // В конце "убиваем" клетки на левой и правой границе, так как
    // предыдущие манипуляции могли их поменять
    for (int j = 0; j < HEIGHT; j++)
    {
        Set(0, j, false);
        Set(WIDTH - 1, j, false);
    }

}


А вот реализация методов get и set усложняется. К счастью, эти методы практически не влияют на производительность, так что можно не слишком беспокоиться по этому поводу. Также обратите внимание на технический трюк: для корректной работы алгоритма пришлось добавить по одной пустой строчке в начало и в конец массива, чтобы избежать проверок на выход за границы массива.

get и set 
public unsafe class LifeIsABitMagic : LifeJourney
{
    byte[] field = new byte[WIDTH + WIDTH * HEIGHT / 2];
    byte[] temp = new byte[WIDTH + WIDTH * HEIGHT / 2];

    public override bool Get(int i, int j)
    {
        int pos = WIDTH / 2 + j * (WIDTH / 2) + (i / 2);
        if (i % 2 == 1) return (field[pos] & 0x10) == 0x10;
        else return (field[pos] & 1) == 1;
    }

    public override void Set(int i, int j, bool val)
    {
        int pos = WIDTH / 2 + j * (WIDTH / 2) + (i / 2);
        if (i % 2 == 1)
        {
            if (val) field[pos] |= 0x10;
            else field[pos] &= (0xFF & ~0x10);
        }
        else
        {
            if (val) field[pos] |= 0x1;
            else field[pos] &= (0xFF & ~0x1);
        }
    }
    ...
}


Вот результат:

Алгоритм: LifeIsABitMagic
Время работы: 1.3 секунды
Скорость работы: 770 шагов в секунду
Ускорение от предыдущей версии: 2.6
Ускорение от первой версии: 31

Исходный код: LifeIsABitMagic.cs

7. Используем SIMD-инструкции процессора


Каждая последующая оптимизация дается нам все большим трудом, так что в этот раз мы пойдем другим путем и используем, пожалуй, самый мощный из доступных на сегодняшний момент способов оптимизации: SIMD-инструкции, а точнее, набор инструкций AVX2, доступный на большинстве современных процессоров Intel и AMD, и позволяющий производить операции над 32 байтами за раз! Этот способ не всегда применим, однако наш случай (работа с байтами и отсутствие ветвлений) идеально ложится на идеологию SIMD, поэтому мы можем ожидать значительного улучшения производительности. Еще несколько лет назад это было доступно только в языках низкого уровня. Нас бы это не остановило: ради оптимизации мы бы скомпилировали библиотеку на C++ и использовали из C# через механизм P/Invoke. Однако буквально год назад в .NET Core появилась встроенная поддержка этого набора инструкций, об этом была даже статья на Хабре. Так что теперь мы можем использовать эту «тяжелую артиллерию» напрямую в C#! За основу возьмем предпоследнюю версию алгоритма LifeInBits, хранящую одну клетку на байт (по причинам, выходящим за рамки этой статьи), и заменим ручную манипуляцию байтами, битами и восьмибайтными словами на соответствующие AVX2-инструкции. При этом, как ни странно, код даже стал проще и понятней!

простой и понятный код 
public AdvancedLifeExtensions()
{  // проверим, что мы не на Pentium III
    if (!Avx2.IsSupported) throw new NotImplementedException("Not in this life!!!");
}

public override void Step()
{
    fixed (byte* fieldPtr = field, tempPtr = temp)
    {
        Vector256<byte> zero = Vector256<byte>.Zero; // тут 32 нуля
        for (int i = 0; i < WIDTH * HEIGHT; i += 32)
        {
            Avx.Store(tempPtr + i, zero);
        }

        for (int i = WIDTH; i < WIDTH * HEIGHT - WIDTH; i += 32)
        {
            Vector256<byte> src1 = Avx.LoadVector256(fieldPtr + i - WIDTH - 1);
            Vector256<byte> src2 = Avx.LoadVector256(fieldPtr + i - WIDTH);
            Vector256<byte> sum1 = Avx2.Add(src1, src2);
            Vector256<byte> src3 = Avx.LoadVector256(fieldPtr + i - WIDTH + 1);
            Vector256<byte> src4 = Avx.LoadVector256(fieldPtr + i - 1);
            Vector256<byte> sum2 = Avx2.Add(src3, src4);
            Vector256<byte> src5 = Avx.LoadVector256(fieldPtr + i + 1);
            Vector256<byte> src6 = Avx.LoadVector256(fieldPtr + i + WIDTH - 1);
            Vector256<byte> sum3 = Avx2.Add(src5, src6);
            Vector256<byte> src7 = Avx.LoadVector256(fieldPtr + i + WIDTH);
            Vector256<byte> src8 = Avx.LoadVector256(fieldPtr + i + WIDTH + 1);
            Vector256<byte> sum4 = Avx2.Add(src7, src8);

            Vector256<byte> sum5 = Avx2.Add(sum1, sum2);
            Vector256<byte> sum6 = Avx2.Add(sum3, sum4);
            Vector256<byte> sum = Avx2.Add(sum5, sum6);

            Avx.Store(tempPtr + i, sum);
        }

        for (int i = WIDTH; i < WIDTH * HEIGHT - WIDTH; i += 32)
        {
            Vector256<byte> neighbours = Avx.LoadVector256(tempPtr + i);
            Vector256<byte> alive = Avx.LoadVector256(fieldPtr + i);

            // в v_1 тридцать два байта единичек
            Vector256<byte> isAlive = Avx2.CompareEqual(alive, v_1);
            // в v_2 тридцать два байта двоек
            Vector256<byte> isTwoNeighbours = Avx2.CompareEqual(neighbours, v_2);
            // в v_3 тридцать два байта троек
            Vector256<byte> isThreeNeighbours = Avx2.CompareEqual(neighbours, v_3);

            Vector256<byte> isTwoOrThreeNeighbours = Avx2.Or(isTwoNeighbours, isThreeNeighbours);
            Vector256<byte> aliveAndNeighbours = Avx2.And(isAlive, isTwoOrThreeNeighbours);

            Vector256<byte> shouldBeAlive = Avx2.Or(aliveAndNeighbours, isThreeNeighbours);
            shouldBeAlive = Avx2.And(shouldBeAlive, v_1);

            Avx2.Store(fieldPtr + i, shouldBeAlive);
        }

    }

    for (int j = 1; j < HEIGHT - 1; j++)
    {
        field[j * WIDTH] = 0;
        field[j * WIDTH + WIDTH - 1] = 0;
    }

}


Этот подход дает нам самую большую оптимизацию (в сто раз по сравнению с изначальным алгоритмом, так что название статьи — правда)!

Алгоритм: AdvancedLifeExtensions
Время работы: 0.4 секунды
Скорость работы: 2500 шагов в секунду
Ускорение от предыдущей версии: 3.2
Ускорение от первой версии: 100

Исходный код: AdvancedLifeExtensions.cs

Это все?


Для полноты картины надо упомянуть еще две оптимизации, которых мы не коснулись:

  1. Перенос вычислений на видеокарту — поскольку алгоритм хорошо ложится на логику SIMD, можно ожидать ускорения еще на порядок. Именно на нем исследователи игры «Жизнь» (да, есть и такие!) ищут новые интересные фигуры методом перебора. К сожалению, код для обработки данных на видеокарте пока еще невозможно написать на .NET.
  2. Сложность всех рассмотренных алгоритмов линейна по времени и площади поля. Существует алгоритм Hashlife, в некоторых ситуациях имеющий логарифмическую сложность по времени и площади! Именно этот алгоритм используется для симуляции огромных систем на миллионы и миллиарды итераций. Тем не менее, существуют плохие начальные условия, при которых этот алгоритм будет значительно медленнее классических, как минимум, на начальном этапе.

JavaScript


Наконец-то мы дошли до самого интересного: можно ли эти оптимизации перенести в JavaScript?

К сожалению, SIMD-версию использовать невозможно, поскольку AVX2 туда еще не завезли. Однако, как ни удивительно, предпоследнюю версию с битовой магией и упаковкой по две клетки в один байт вполне можно использовать, правда не восьмибайтный вариант, а только четырехбайтный.

Трюк здесь в том, что в JavaScript есть специальные классы, позволяющие работать с массивом байт одновременно и как с байтами, и как с числами: UInt8Array и UInt32Array. При этом можно перенести код практически дословно (с поправкой на обработку четырех байт вместо восьми) и надеяться, что JIT-компилятор яваскриптового движка сможет обработать нашу битовую арифметику без конвертации в числа с плавающей точкой.

Код на JavaScript 
class LifeField {
    constructor() {
        this.field = new ArrayBuffer(LifeField.WIDTH + LifeField.WIDTH * LifeField.HEIGHT / 2);
        this.temp = new ArrayBuffer(LifeField.WIDTH + LifeField.WIDTH * LifeField.HEIGHT / 2);
        this.fieldBytes = new Uint8Array(this.field);
        this.tempBytes = new Uint8Array(this.temp);
        this.fieldInts = new Uint32Array(this.field);
        this.tempInts = new Uint32Array(this.temp);
    }

    get(x, y) { 
        const pos = LifeField.WIDTH / 2 + y * (LifeField.WIDTH / 2) + (x >> 1);
        if ((x & 1) == 1) return (this.fieldBytes[pos] & 0x10) == 0x10;
        else return (this.fieldBytes[pos] & 1) == 1;
    }

    set(x, y, val) { ... } //аналогично
    
    step() {
        for(var i = 0; i < this.tempInts.length; i++) this.tempInts[i] = 0;

        for (var j = LifeField.WIDTH; j < LifeField.WIDTH * LifeField.HEIGHT / 2; j += 4)
        {
            const i = j / 4;

            const src1 = this.fieldInts[i - LifeField.WIDTH / 8];
            const src2 = this.fieldInts[i];
            const src3 = this.fieldInts[i + LifeField.WIDTH / 8];

            const src4 = this.fieldInts[i - LifeField.WIDTH / 8 - 1];
            const src5 = this.fieldInts[i - 1];
            const src6 = this.fieldInts[i + LifeField.WIDTH / 8 - 1];

            const src7 = this.fieldInts[i - LifeField.WIDTH / 8 + 1];
            const src8 = this.fieldInts[i + 1];
            const src9 = this.fieldInts[i + LifeField.WIDTH / 8 + 1];

            this.tempInts[i] += (src1 << 4) + src1 + (src1 >> 4);
            this.tempInts[i] += (src2 << 4) + (src2 >> 4);
            this.tempInts[i] += (src3 << 4) + src3 + (src3 >> 4);

            this.tempInts[i] += (src4 >> 28) + (src5 >> 28) + (src6 >> 28);
            this.tempInts[i] += (src7 << 28) + (src8 << 28) + (src9 << 28);
        }

        for (var j = LifeField.WIDTH; j < LifeField.WIDTH * LifeField.HEIGHT / 2; j += 4) {
            const i = j / 4;
            const neighbours = this.tempInts[i] & 0x77777777;
            const alive = this.fieldInts[i];

            var keepAlive = ((neighbours & ~0x11111111) >> 1) | (alive << 2);
            keepAlive ^= ~0x55555555;
            keepAlive &= (keepAlive >> 2);
            keepAlive &= (keepAlive >> 1);
            keepAlive &= 0x11111111;

            var makeNewLife = neighbours | (alive << 3);
            makeNewLife ^= ~0x33333333;
            makeNewLife &= (makeNewLife >> 2);
            makeNewLife &= (makeNewLife >> 1);
            makeNewLife &= 0x11111111;

            this.fieldInts[i] = keepAlive | makeNewLife;
        }

        for(var y = 1; y < LifeField.WIDTH - 1; y++) {
            this.set(0, y, false);
            this.set(LifeField.WIDTH - 1, y, false);
        }
    }
    ...
}
LifeField.WIDTH = 1920;
LifeField.HEIGHT = 1080;


Вот результат:

Алгоритм: LifeIsABitMagic (JavaScript 32 bit), вне конкурса
Время работы: 5 секунд
Скорость работы: 200 шагов в секунду
Ускорение от предыдущей версии: -
Ускорение от первой версии: 8

Полный код в файле lifefield.js

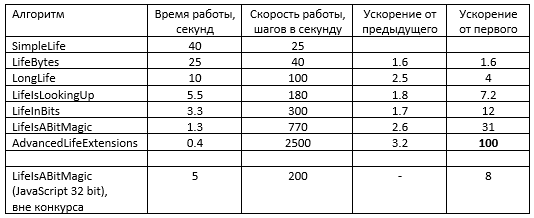
В заключение сводная таблица со всеми алгоритмами:

image

Онлайн-игра


Напоследок самое интересное: на основе этого алгоритма была написана онлайн-игра, стабильно быстро работающая на поле размера 1920x1080 (Full HD) при любой начальной конфигурации:

играть в симуляцию игры «Жизнь» image

Исходные коды опубликованы на гитхабе.