15.06.2020 11:10
AntonSt 16 2100 Источник
Энергетика – обширная сфера деятельности, и расчеты в ней производятся разные: расчет рентабельности строительства новых станций, расчет перенапряжений, расчет оставшегося времени до конца рабочего дня в пятницу вечером. Все эти темы в одной статье не уместить, поэтому сконцентрируюсь на той, которой занимался в течение последних лет, – расчеты переходных процессов в электрических сетях. Кому интересно, что это такое и как оно происходит в современном мире, – прошу под кат.

Оглавление


  • Зачем вообще что-то рассчитывать в энергетике?
  • Переходные процессы – это…
  • Переходные процессы и режим реального времени
  • Нельзя просто так взять и рассчитать переходный процесс
  • Куда и как запустить модель?
  • Управление по управлению всеми управлениями
  • Все уже сделано до нас
  • Заключение

Зачем вообще что-то рассчитывать в энергетике?


Причины довольно стандартны для любой технической/инженерной сферы: экономия, безопасность, нормативы и прочие банальности. Несколько примеров:

  • Чем точнее мы знаем, какие перенапряжения могут возникнуть, тем меньше денег можно затратить на изоляционный материал, имеющий достаточный запас прочности.
  • Чем больше информации имеется о резонансных частотах в сети, тем точнее можно настроить систему управления и эффективнее справляться с воздействием внешних факторов.
  • Чем детальнее изучено поведение оборудования в тех или иных режимах, тем проще соблюсти нормативы, пройти сертификацию или приёмку.
  • И т. д.
  • И т. п.

Что объединяет приведенные выше примеры? То, каким образом можно получить всю эту интересующую нас информацию. Те, кто помнит название статьи, уже догадались: это можно сделать, рассчитав переходные процессы.

Впрочем, если у вас есть деньги и время для проведения экспериментов, то можно одними расчетами не ограничиваться, ведь теория – это хорошо, а теория, подкрепленная экспериментами, – еще лучше. Правда это может быть долго, дорого и не всегда возможно, ведь ставить эксперименты на работающей энергосистеме – это, выражаясь местным сленгом, сродни запуску тестов на продакшн сервере – если что-то пойдет не так, то мало не покажется.

Ну а если нет ни времени, ни денег, ни желания проводить расчеты
то придется либо везде закладывать значительный запас прочности, либо подвергать риску человеческие жизни.

Переходные процессы – это…


Если по-простому, переходный процесс – это когда токи и напряжения в электрической сети изменяются во времени вследствие различных событий, таких как короткие замыкания, отключения выключателей, удары молнии и проч. и проч. Переходные процессы – явления чаще всего временные. В электроэнергетике они могут длиться как нано- и микросекунды (переключение транзисторов, удары молнии), так и несколько минут или часов (межсистемные колебания, электромагнитные бури).

Рассчитать переходный процесс – значит узнать, как именно изменяются токи и напряжения.

Переходные процессы обычно плавно перетекают в установившиеся. В установившемся процессе, если опять же по-простому, величины токов и напряжений постоянны. «А как же напряжение в розетке, которое меняется 50 раз в секунду?» – спросите вы. В принципе, это тоже можно рассматривать как непрекращающийся переходный процесс, но если амплитуда, частота и фаза синусоидального сигнала постоянны, то гораздо удобнее рассматривать как установившийся. Для этого существуют свои методы, но об этом как-нибудь в другой раз.

Кто круче, переходные или установившиеся процессы?
Все самое интересное происходит во время переходных процессов. Если при изучении установившихся меня посещают мысли типа «Шок! В номинальных условиях оборудование выдает номинальный ток», то при расчете переходных можно, например, узнать, что недостаточная нагрузка на линии электропередач может привести к феррорезонансу и перенапряжениям, из-за чего многомиллионное оборудование сгорит или взорвется (события вымышлены, совпадения случайны).

Вот, например, напряжения на конденсаторе при подключении его к трехфазной сети 10 кВ (если что, конденсаторов на самом деле три – по одному на каждую фазу):


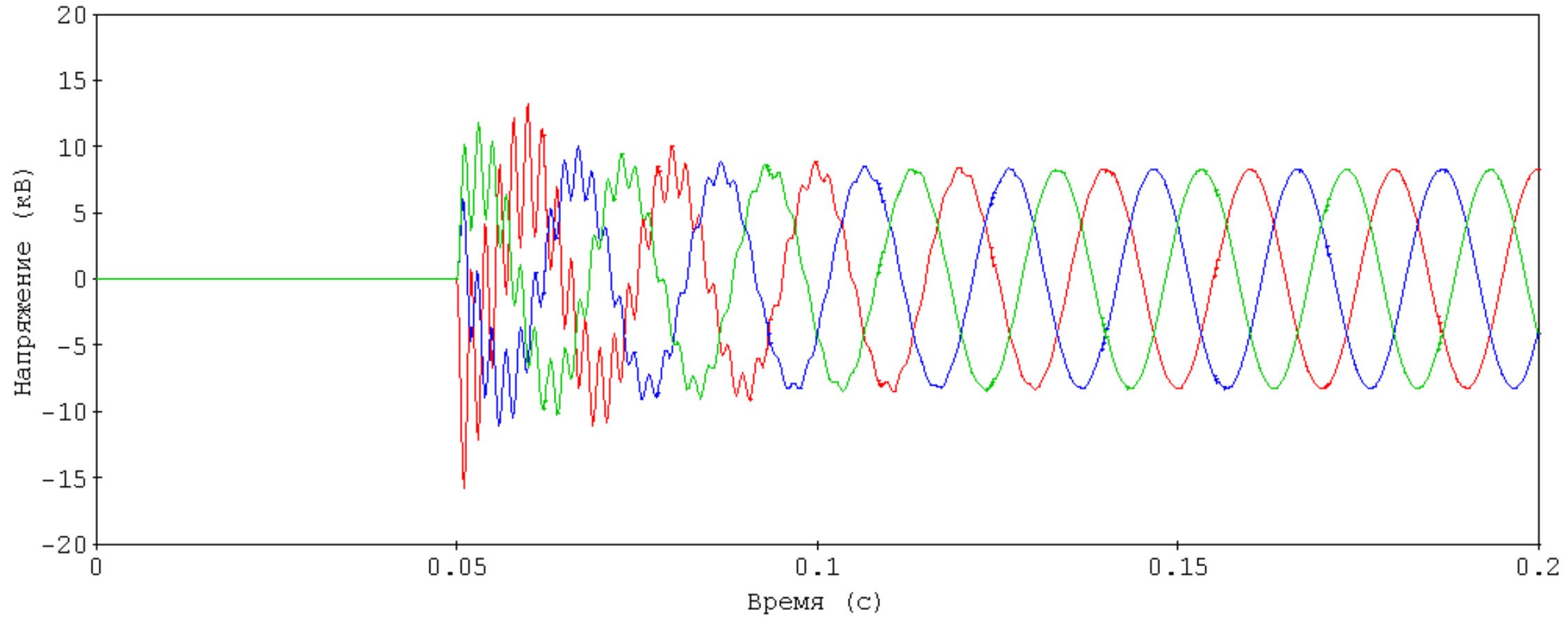
Где-то сейчас замигали лампочки

Вопрос: когда начинается переходный процесс?

Вопрос со звездочкой: когда заканчивается переходный процесс и начинается установившийся?

Ответы
Начинается переходный процесс в 0.05 с и переходит в установившийся примерно в 0.13 с.
Но если к вопросу подходить с математической точностью, то переходный процесс здесь вообще никогда не заканчивается, так как описывается дифференциальными уравнениями с решениями в виде экспонент. А экспоненты, даже затухающие, к нулю только стремятся. Но об этом чуть позже.

Переходные процессы и режим реального времени


Есть еще одна область применения расчетов переходных процессов – это расчеты в реальном времени. Если обычно все гонятся за уменьшением времени расчетов, то здесь, наоборот, очень важно, чтобы расчет одной секунды проходил ровно за одну секунду. Это применяется, например, для прототипирования, тестирования и отладки устройств, предназначенных для взаимодействия с реальным миром: систем управления, защиты и т.д.

Поясню на примере: система управления электростанцией знает, что для реакции на событие X электростанции понадобится две секунды, а на событие Y – три. Чтобы дебажить эту систему управления, её подключают не к реальной электростанции, а к так называемому симулятору, имитирующему поведение электростанции. Симулятор в реальном времени рассчитывает переходные процессы, которые происходили бы в электростанции, и ведет себя соответствующе: отвечает на событие X за две секунды, а на Y – за три вне зависимости от количества ядер процессора и тактовой частоты. Система управления при этом думает, что работает с реальной электростанцией.


Слева: система управления и электростанция дружно работают на благо родины.
Справа: ничего не подозревающая система управления коварно обманута и подключена к симулятору

Нельзя просто так взять и рассчитать переходный процесс


В рассчитываемой электрической сети могут иметься тысячи различных компонентов, поэтому ручной расчет переходных процессов практически неприменим к реальным задачам в электроэнергетике – все считается на компьютере. Расчеты переходных процессов в реальном времени производить вручную еще сложнее, ведь вам понадобится еще и секундомер.

Ну и
сверхчеловеческая скорость тоже не помешает, т. к. новые данные надо выдавать раз в несколько микросекунд.

В начале расчета стоит определиться, какая от него требуется информация. Например, нам нужно узнать перенапряжения, возникающие при коротком замыкании в преобразователе постоянного тока на морской ветроэлектростанции. С типом расчетов всё и так понятно из названия статьи – нужно рассчитывать переходные процессы.


Вот так схематично эта система может выглядеть

Затем нужно разработать математическую модель рассчитываемой системы: ветровой электростанции, преобразователей, кабеля и прилегающей электрической сети. Этот этап может быть довольно сложным, ведь не всегда сразу ясно, насколько детальны должны быть модели. Чем больше деталей, тем точнее результат, но тем больше времени надо потратить на расчеты. Никто не любит долго ждать, поэтому приходится искать компромисс. Часто для удовлетворительной точности требуются многие десятки дифференциальных и не очень уравнений для каждого устройства.

Как только модель системы у нас появилась, можно запустить её в солвер (об этом чуть дальше), задать начальные условия и все рассчитать. Как происходит типичный расчет:

  • Интересующий период времени разбивается на отрезки с шагом интегрирования ?t. Чем меньше шаг интегрирования, тем медленнее процесс расчета и точнее результаты. Часто используются величины ?t от единиц до десятков микросекунд.
  • Величины токов и напряжений в момент времени (t-?t) используются для расчета величин на следующем моменте времени (t).
  • Начальные условия, т. е. начальные величины токов и напряжений, находятся из предположения, что в момент времени t=0 был установившийся режим.

Когда расчет закончен, можно использовать результаты по назначению (ну или обнаружить перенапряжения в миллиарды вольт и понять, что кто-то перепутал плюс с минусом).

Куда и как запустить модель?


Основу ПО для расчета переходных процессов составляет солвер – программа, решающая систему уравнений. Особую популярность в области переходных процессов имеют солверы, основанные либо на методе узловых потенциалов, либо на методе пространства состояний. Метод пространства состояний подходит для практически любых систем дифференциальных уравнений, а в методе узловых потенциалов используются законы Ома и Кирхгофа, что делает его удобным именно для электрических систем.

Дифференциальные уравнения математических моделей нужно привести к удобоваримому для солвера виду, т. е. к превратить их в систему линейных алгебраических уравнений. Для этого применяется численное интегрирование. Часто используется метод трапеций, его и рассмотрим. Все уравнения ветровой электростанции из предыдущей главы здесь писать не буду, ограничусь одним скромным конденсатором. Ток и напряжение на нем связывает дифференциальное уравнение вида

$$display$$i=C \frac{du}{dt}$$display$$


Пошаговый расчет методом трапеций для любопытных
Сначала перейдем к конечным разностям:

$$display$$i=C\frac{\Delta u}{\Delta t}$$display$$


Применим суть метода трапеций на двух последовательных моментах времени (t-?t) и (t):

$$display$$\frac{i(t)+i(t-?t)}{2}=C \frac{u(t)-u(t-\Delta t)}{\Delta t}$$display$$


А теперь вынесем величины для момента времени (t-?t) в отдельное слагаемое:

$$display$$i(t)=u(t) \frac{2C}{\Delta t} - \left[i (t-\Delta t) + u(t-?t) \frac{2C}{\Delta t} \right]$$display$$


Тем, кому хочется попробовать свои силы самостоятельно, предлагаю разделаться таким же образом с уравнением для индуктивности.

Уравнение конденсатора после метода трапеций:

$$display$$i(t)=u(t) \frac{2C}{\Delta t} - \left[i (t-\Delta t) + u(t-?t) \frac{2C}{\Delta t} \right]$$display$$


Величины для момента времени (t-?t) вынесены в отдельное слагаемое, т. к. известны из расчета предыдущего момента времени. Теперь вместо дифференциального у нас есть обычное линейное алгебраическое уравнение. Если подключить фантазию, то можно заметить, что финальное уравнение очень похоже на резистор, подключенный параллельно с источником тока.

Не вижу тут никаких резисторов, одни формулы!
Если что, величина резистора равна $inline$\frac{\Delta t}{2C}$inline$, а источника тока $inline$\left[- i(t-\Delta t) - u(t-?t) \frac{2C}{\Delta t} \right]$inline$.

Аналогичным образом уравнения других элементов приводятся к комбинациям резисторов и источников тока. А такие электрические схемы умеет решать каждый уважающий себя солвер, основанный на методе узловых потенциалов.


Легким движением руки схема превращается…

Не все элементы в электрических сетях представляются в виде резисторов и источников тока, но все в итоге представляются в виде линейных алгебраических уравнений, которые можно скормить солверу. А если не представляются в виде линейных, то можно линеаризовать, рассчитать якобиан, применить метод Ньютона, но все равно решить, пусть и с итерациями. Но не будем сильно углубляться, об этом тоже как-нибудь в другой раз.

Управление по управлению всеми управлениями


В реальных электрических сетях очень часто используются системы управления: в электроприводе, в ветровых генераторах, в преобразователях постоянного/переменного тока и т. д. Они оказывают сильное влияние на переходные процессы, поэтому их тоже приходится учитывать в расчетах.

Сложность уравнений в системах управления теоретически ограничена лишь фантазией инженеров: дискретные передаточные функции пятого порядка? Пожалуйста. Синус от логарифма? Дайте два, один гиперболический. Из-за этого солвер для систем управления часто приходится использовать отдельный, посложнее.

Впрочем, часто системы управления «однонаправлены», т. е. сигналы приходят с датчиков, проходят обработку и отправляются в управляющие устройства (типа транзисторов) без каких-либо самозацикливаний. Расчет такой системы управления относительно прост, ведь можно последовательно применять всякие алгебраические операции и горя не знать.


Два сложения, два умножения и один интеграл. Легкотня!

Про направление систем управления
К сожалению, иногда выходные сигналы приходится подавать себе самому на вход, что называется алгебраической петлей (algebraic loop). Это усложняет расчеты, так как вместо последовательных операций теперь надо решать систему уравнений, возможно даже нелинейных. Этого особо никто не любит, т. к. приходится либо итерировать, либо как-то разрывать этот порочный loop. Например, вставляя задержки между выходом и входом. Все это может негативно сказываться на точности и/или скорости расчетов.

Все уже сделано до нас


Ну а если не хочется самому разрабатывать модели и солверы, можно воспользоваться уже существующими программными продуктами. Приведу лишь широко известные в узких кругах энергетиков программы, ибо составить исчерпывающий список – задача не из простых. У меня бэкграунд скорее энергетика, чем электронщика, поэтому некоторые популярные программы со схожим функционалом из области электроники наверняка пропустил. Если знаете что-то похожее – поделитесь в комментариях.

  • EMTP: специализированное ПО для расчета переходных процессов в электрических сетях. Может использоваться и для расчета установившихся процессов
  • ATP: то же самое
  • PSCAD: то же самое
  • PowerFactory: то же самое
  • Simulink: популярен, знаменит, много методов интегрирования. Но для электрических сетей с большим количеством элементов подходит с трудом. А для прототипирования – очень даже.
  • SimPowerSystems: надстройка над Simulink’ом специально для электрических систем.
  • Hypersim: расчеты в реальном времени
  • RTDS: тоже расчеты в реальном времени
  • PSS/E: может как и в установившиеся, так и в переходные процессы
  • LTspice: с упором на электронику

Половина этих продуктов из Канады: EMTP, PSCAD, SimPowerSystems, Hypersim, RTDS. Не скажу, с чем связан такой интерес канадцев к переходным процессам, но разбираются они в них не хуже, чем в хоккее.

Заключение


Надеюсь, было познавательно. Ну или хотя бы не очень скучно – целых пять картинок в статье, как-никак.