Поиск функциональных зависимостей в данных применяется в разных направлениях анализа данных: управление базами данных, очистка данных, ревёрс-инжиниринг баз данных и эксплорация данных. Про сами зависимости мы уже публиковали статью Анастасии Бирилло и Никиты Боброва. В этот раз Анастасия — выпускница Computer Science Center этого года — делится развитием этой работы в рамках НИР, которую она защитила в центре.

Во время обучения в CS центре я начала углублённо изучать базы данных, а именно, поиск функциональных и разностных зависимостей. Эта тема была связана с темой моей курсовой в университете, так что во время работы над курсовой я начала читать статьи про различные зависимости в базах данных. Я написала обзор этой области — одну из первых своих статей на английском языке и подала её на конференцию SEIM-2017. Я была очень рада, когда узнала, что её всё же приняли, и решила углубиться в тему. Сама концепция не новая — её начали применять еще в 90х годах, но и сейчас она находит применение во многих областях.
Во втором семестре обучения в центре я начала научно-исследовательский проект по улучшению алгоритмов поиска функциональных зависимостей. Работала над ним вместе с аспирантом СПбГУ Никитой Бобровым на базе JetBrains Research.
Основная проблема — вычислительная трудоёмкость. Число возможных минимальных и нетривиальных зависимостеи? ограничено сверху значением , где — число атрибутов таблицы. Время работы алгоритмов зависит не только от количества атрибутов, но и от количества строк. В 90-х годах алгоритмы по поиску ФЗ на обычном настольном ПК могли обрабатывать наборы данных, содержащие до 20 атрибутов и десятки тысяч строк, до нескольких часов. Современные алгоритмы, работающие на многоядерных процессорах, обнаруживают зависимости для наборов данных, состоящих из сотен атрибутов (до 200) и сотен тысяч строк, примерно за то же время. Тем не менее этого недостаточно: такое время неприемлемо для большинства реальных приложении?. Поэтому мы разрабатывали подходы для ускорения существующих алгоритмов.
В первой части работы мы разработали схемы кэширования для класса алгоритмов, использующих метод пересечения партиций. Партиция для атрибута представляет собои? набор списков, где каждыи? список содержит номера строк с одинаковыми значениями для данного атрибута. Каждый такой список называется кластер. Многие современные алгоритмы используют партиции для определения, удерживается зависимость или нет, а именно придерживаются леммы: Зависимость удерживается, если . Здесь обозначается партиция и используется понятие размер партиции — количество кластеров в ней. Алгоритмы, использующие партиции, при нарушении зависимости добавляют дополнительные атрибуты в левую часть зависимости, после чего пересчитывают её, производя операцию пересечения партиций. Такая операция в статьях называется специализацией. Но мы заметили, что партиции для зависимостей, которые будут удержаны лишь после нескольких раундов специализации, могут быть активно переиспользованы, что может существенно сократить время работы алгоритмов, так как операция пересечения является дорогой.
Поэтому мы предложили эвристику, основанную на Энтропии Шеннона и неопределённости Джинни, а также нашей метрике, которую мы назвали Обратная Энтропия. Она является незначительной модификацией Энтропии Шеннона и растёт по мере того, как растёт уникальность набора данных. Предложенная эвристика выглядит следующим образом:
Здесь — степень уникальности недавно вычисленнои? партиции , а является медианои? степенеи? уникальности для отдельных атрибутов. В качестве метрики уникальности были опробованы все три метрики, описанные выше. Также можно заметить, что в эвристике присутствуют два модификатора. Первый указывает, насколько близка текущая партиция к первичному ключу и позволяет в большеи? степени кэшировать те партиции, которые далеки от потенциального ключа. Второй модификатор позволяет отслеживать занятость кэша и тем самым стимулирует добавление большего количества партиции? в кэш при наличии свободного места. Успешное решение этой задачи позволило ускорить алгоритм PYRO на 10-40% процентов в зависимости от датасета. Стоит отметить, что алгоритм PYRO является наиболее успешным в этой области.
На рисунке ниже можно увидеть результаты применения предложенной эвристики по сравнению с базовым подходом по кэшированию, основанном на подбрасывании монетки. Ось X логарифмическая.

Затем мы предложили альтернативный способ хранения партиций. Партиции представляют собои? набор кластеров, в каждом из которых хранятся номера кортежеи? с одинаковыми значениями по определённым атрибутам. Эти кластеры могут содержать длинные последовательности номеров кортежеи?, например, если в таблице данные упорядочены. Поэтому мы предложили схему сжатия для хранения партиции?, а именно интервальное хранение значении? в кластерах партиции?:
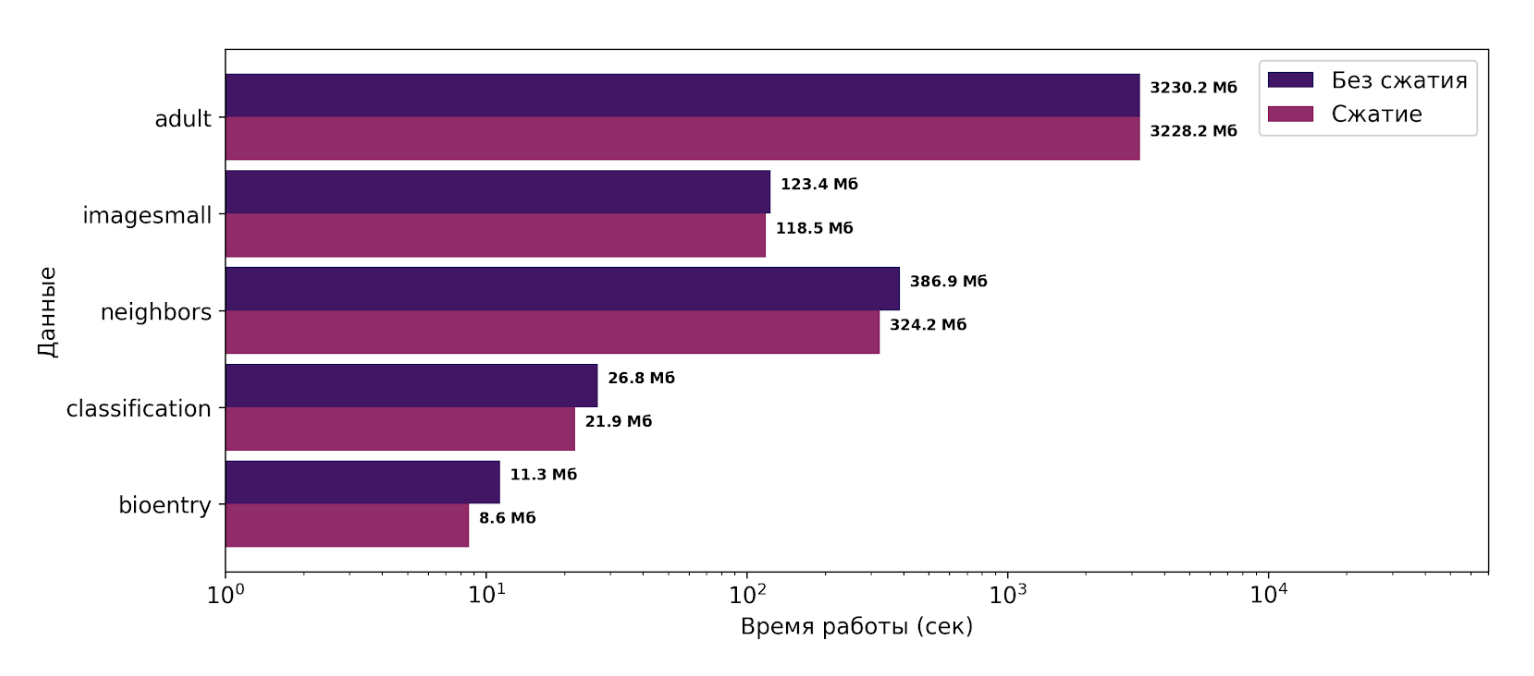
Этот метод смог сократить потребление памяти во время работы алгоритма TANE от 1 до 25%. Алгоритм TANE — классический алгоритм по поиску ФЗ, он использует партиции в ходе своей работы. В рамках практики был выбран именно алгоритм TANE, так как внедрить в него интервальное хранение было значительно проще, чем, например, в PYRO, чтобы оценить, работает ли предлагаемый подход. Полученные результаты представлены на рисунке ниже. Ось X логарифмическая.
По результатам исследования в сентябре 2019 года я выступила со статьёй Smart Caching for Efficient Functional Dependency Discovery на конференции 23rd European Conference on Advances in Databases and Information Systems (ADBIS-2019). Во время выступления работу отметил Bernhard Thalheim, значимый человек в области баз данных. Результаты исследований легли в основу моей диссертации в магистратуре мат-меха СПбГУ, в ходе которой оба предложенных подхода (кэширование и сжатие) были внедрены в оба алгоритма: TANE и PYRO. При этом результаты показали, что предложенные подходы являются универсальными, так как на обоих алгоритмах при обоих подходах наблюдалось значительное сокращение потребляемой памяти, а также значительное сокращение времени работы алгоритмов.

Выбор задачи
Во время обучения в CS центре я начала углублённо изучать базы данных, а именно, поиск функциональных и разностных зависимостей. Эта тема была связана с темой моей курсовой в университете, так что во время работы над курсовой я начала читать статьи про различные зависимости в базах данных. Я написала обзор этой области — одну из первых своих статей на английском языке и подала её на конференцию SEIM-2017. Я была очень рада, когда узнала, что её всё же приняли, и решила углубиться в тему. Сама концепция не новая — её начали применять еще в 90х годах, но и сейчас она находит применение во многих областях.
Во втором семестре обучения в центре я начала научно-исследовательский проект по улучшению алгоритмов поиска функциональных зависимостей. Работала над ним вместе с аспирантом СПбГУ Никитой Бобровым на базе JetBrains Research.
Вычислительная трудоёмкость поиска функциональных зависимостей
Основная проблема — вычислительная трудоёмкость. Число возможных минимальных и нетривиальных зависимостеи? ограничено сверху значением , где — число атрибутов таблицы. Время работы алгоритмов зависит не только от количества атрибутов, но и от количества строк. В 90-х годах алгоритмы по поиску ФЗ на обычном настольном ПК могли обрабатывать наборы данных, содержащие до 20 атрибутов и десятки тысяч строк, до нескольких часов. Современные алгоритмы, работающие на многоядерных процессорах, обнаруживают зависимости для наборов данных, состоящих из сотен атрибутов (до 200) и сотен тысяч строк, примерно за то же время. Тем не менее этого недостаточно: такое время неприемлемо для большинства реальных приложении?. Поэтому мы разрабатывали подходы для ускорения существующих алгоритмов.
Схемы кэширования для пересечения партиций
В первой части работы мы разработали схемы кэширования для класса алгоритмов, использующих метод пересечения партиций. Партиция для атрибута представляет собои? набор списков, где каждыи? список содержит номера строк с одинаковыми значениями для данного атрибута. Каждый такой список называется кластер. Многие современные алгоритмы используют партиции для определения, удерживается зависимость или нет, а именно придерживаются леммы: Зависимость удерживается, если . Здесь обозначается партиция и используется понятие размер партиции — количество кластеров в ней. Алгоритмы, использующие партиции, при нарушении зависимости добавляют дополнительные атрибуты в левую часть зависимости, после чего пересчитывают её, производя операцию пересечения партиций. Такая операция в статьях называется специализацией. Но мы заметили, что партиции для зависимостей, которые будут удержаны лишь после нескольких раундов специализации, могут быть активно переиспользованы, что может существенно сократить время работы алгоритмов, так как операция пересечения является дорогой.
Поэтому мы предложили эвристику, основанную на Энтропии Шеннона и неопределённости Джинни, а также нашей метрике, которую мы назвали Обратная Энтропия. Она является незначительной модификацией Энтропии Шеннона и растёт по мере того, как растёт уникальность набора данных. Предложенная эвристика выглядит следующим образом:
Здесь — степень уникальности недавно вычисленнои? партиции , а является медианои? степенеи? уникальности для отдельных атрибутов. В качестве метрики уникальности были опробованы все три метрики, описанные выше. Также можно заметить, что в эвристике присутствуют два модификатора. Первый указывает, насколько близка текущая партиция к первичному ключу и позволяет в большеи? степени кэшировать те партиции, которые далеки от потенциального ключа. Второй модификатор позволяет отслеживать занятость кэша и тем самым стимулирует добавление большего количества партиции? в кэш при наличии свободного места. Успешное решение этой задачи позволило ускорить алгоритм PYRO на 10-40% процентов в зависимости от датасета. Стоит отметить, что алгоритм PYRO является наиболее успешным в этой области.
На рисунке ниже можно увидеть результаты применения предложенной эвристики по сравнению с базовым подходом по кэшированию, основанном на подбрасывании монетки. Ось X логарифмическая.

Альтернативный способ хранения партиций
Затем мы предложили альтернативный способ хранения партиций. Партиции представляют собои? набор кластеров, в каждом из которых хранятся номера кортежеи? с одинаковыми значениями по определённым атрибутам. Эти кластеры могут содержать длинные последовательности номеров кортежеи?, например, если в таблице данные упорядочены. Поэтому мы предложили схему сжатия для хранения партиции?, а именно интервальное хранение значении? в кластерах партиции?:
Этот метод смог сократить потребление памяти во время работы алгоритма TANE от 1 до 25%. Алгоритм TANE — классический алгоритм по поиску ФЗ, он использует партиции в ходе своей работы. В рамках практики был выбран именно алгоритм TANE, так как внедрить в него интервальное хранение было значительно проще, чем, например, в PYRO, чтобы оценить, работает ли предлагаемый подход. Полученные результаты представлены на рисунке ниже. Ось X логарифмическая.

Конференция ADBIS-2019
По результатам исследования в сентябре 2019 года я выступила со статьёй Smart Caching for Efficient Functional Dependency Discovery на конференции 23rd European Conference on Advances in Databases and Information Systems (ADBIS-2019). Во время выступления работу отметил Bernhard Thalheim, значимый человек в области баз данных. Результаты исследований легли в основу моей диссертации в магистратуре мат-меха СПбГУ, в ходе которой оба предложенных подхода (кэширование и сжатие) были внедрены в оба алгоритма: TANE и PYRO. При этом результаты показали, что предложенные подходы являются универсальными, так как на обоих алгоритмах при обоих подходах наблюдалось значительное сокращение потребляемой памяти, а также значительное сокращение времени работы алгоритмов.

