Сегодня я хочу рассказать вам о том как я попытался решить проблему Гольдбаха
Проблема Гольдбаха — утверждение о том, что любое чётное число, начиная с 4, можно представить в виде суммы двух простых чисел. То есть 6=3+3; 8=5+3 … Как я понял, решение проблемы — это доказательство или опровержение этого утверждения.

Первое что нам потребуется это реализовать метод для проверки является ли число простым. Простым называется число, которое делится только на самого себя и на единицу.

public static bool IsPrimeNumber(ulong n)
{
    var result = true;
    if (n > 1)
    {
        for (ulong i = 2; i < n; i++)
        {
           if (n % i == 0)
           {
                result = false;
                break;
            }
        }
    }
    else
    {
        result = false;
    }
    return result;
}

Теперь нам необходимо получить коллекцию всех простых чисел до ulong.MaxValue = 18446744073709551615 (2^64-1)

public static IEnumerable<ulong> GetAllPrimeNumbers(ulong maxNumber)
{
    List<ulong> primeNumbers = new List<ulong>();
    for (ulong i=0; i < maxNumber; i++ )
    {
        if (IsPrimeNumber(i))
        {
            primeNumbers.Add(i);
        }
    }
    return primeNumbers;
}

Интуиция подсказывает что вычислять он их будет очень долго так что уменьшим их количество до 300000

static void Main(string[] args)
{
    Stopwatch stopwatch = new Stopwatch();
    stopwatch.Start();
    IEnumerable<ulong> primeNumbers = GetAllPrimeNumbers();
    checkGoldbach(primeNumbers); 
    stopwatch.Stop();
    Console.WriteLine("Потрачено времени " + stopwatch.Elapsed.TotalSeconds + " секунд");
    foreach(var number in primeNumbers)
    {
        Console.Write(number + " ");
    }
    Console.ReadKey();
}

Потом мне захотелось найти все простые число до 2^64 (Как мне казалось, пару часов вычислений мне будет достаточно)
После двух минут работы программы решил поставить точку останова и проверить какое число сейчас проверяется на простоту:

411780 итераций после двух минут вычислений. Решил немного оптимизировать метод проверки простоты числа, так как нет необходимости продолжать итерацию после половины числа

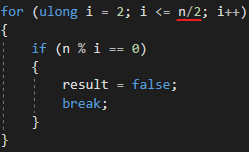
Таким образом уменьшается в двое количество итераций необходимых для проверки простоты. Мне показалось что за 2 минуты количество итераций должна увеличиться в двое

Но и тут я ошибался. Производительность увеличилось не на 100%, а на 22%. Как я потом понял происходит это из-за того, что половина проверок, как и раньше отсеиваются делением на 2, треть всех чисел, не отсеянных делением на 2, отсеиваются делением на 3 и т.д. Из 500154 проверок на простоту было найдено 41549 простых чисел. То есть, итерация for

for (ulong i = 2; i <= n/2; i++)
{
    if (n % i == 0)
    {
        result = false;
        break;
    }
}

исполнялось до конца (без break) всего 41549 раз. В остальных случаях он прерывался раньше…
500154 и близко не 2^64, нужно вычислить сколько времени потребуется для проверки простоты всех чисел до 2^64
Для начало уменьшим количество итераций с 2^64 до 30000 и вычислим время работы метода stopwatch-ом

на перебор чисел до 30000 было потрачено 1 секунда
теперь составим таблицу с другими значениями количества итераций

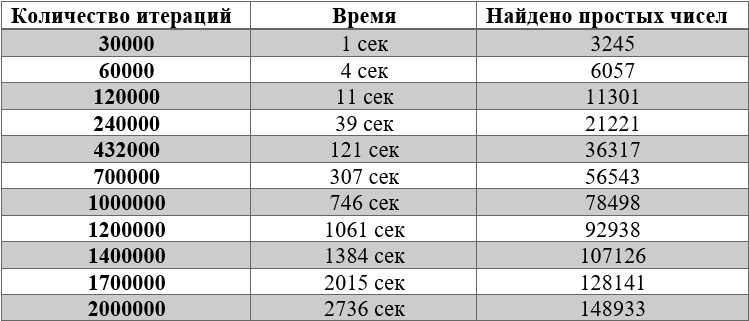
Запишем полученный результат в Excel, и построим график точечный для координат «Количество итераций на время» и «Количество простых чисел на диапазон»


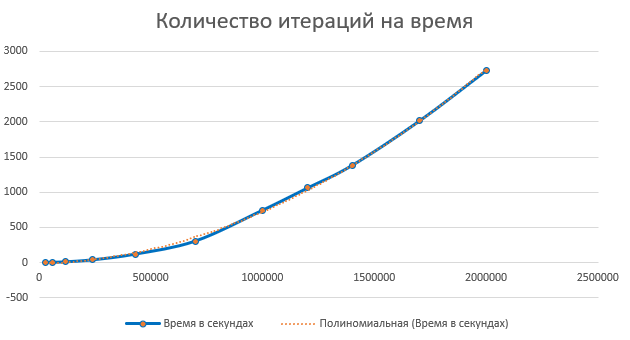
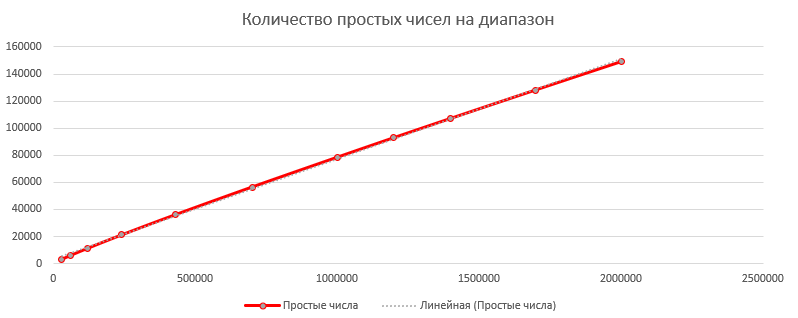
Теперь мы сможем узнать примерное количество простых чисел до 2^64, и сколько примерно уйдет времени, чтобы их всех найти
Если добавить линию тренда «Линейный» на график «количество простых чисел на диапазон» Excel выдаст формулу y=0,074x+3004 (Я не владею информацией насколько формула точна). Это значит что приблизительное количество простых чисел до ulong.MaxValue = 0,074*2^64+3004;
Точно так же добавив линию тренда «Полиномиальная» на график «Количество итераций на время» получим формулу y = 7E-10x2 + 6E-05x. Подставив вместо x наше число 2^64 можно выяснить что для нахождения всех простых чисел до 2^64 нам понадобится приблизительно 2,38E+29 секунд, или же 7553198149564240000000 лет. Ок, столько ожидать я не смогу.
Давайте попытаемся доказать, что гипотеза Гольдбаха верна для всех четных чисел до 300000.

public static void checkGoldbach(IEnumerable<ulong> primeNumbers)
{
    ulong numbersCount = 300000;
    for (ulong number = 4; number<numbersCount; number+=2)
    {
        bool isGoldbachResult = false;
        foreach(ulong primeNumber1 in primeNumbers)
        {
            foreach(ulong primeNumber2 in primeNumbers)
            {
                if(primeNumber1+primeNumber2==number)
                {
                    Console.WriteLine("{0} = {1} + {2}", number, primeNumber1, primeNumber2);
                    isGoldbachResult = true;
                    break;
                }
                if(primeNumber1+primeNumber2>number)
                {
                    break;
                }
            }
            if(isGoldbachResult|| primeNumber1>number)
            {
                break;
            }
        }
        if(!isGoldbachResult)
        {
            Console.WriteLine("Число " + number + " не удалось представить в виде суммы двух простых чисел");
            break;
        }
    }
}

Если утверждение Гольдбаха не справедлива для какого-то числа, метод остановит вычисления на этом числе.

После 9 минут вычислений мы можем утверждать, что гипотеза Гольдбаха справедлива для чисел, не превышающих 300000.

Итого

Все оказалось не так просто, как показалось мне в начале, и я понимаю, что я нисколько не приблизился к решению проблемы.
Скорее всего, мне так кажется, что существует более оптимальные варианты проверки числа на простоту. Возможно, что метод проверяющий четные числа на верность утверждения Гольдбаха можно реализовать рациональнее чем простым перебором простых чисел, но мне уже не так сильно хочется тратить на это время…
Решение проблемы Гольдбаха ничего не даст человечеству. На данный момент было доказано, что гипотеза верна для чисел до 4*10^18, но какой смысл доказывать его для всех чисел? С какой целью математики пишут книги на эту тему и вообще тратят на решение таких «проблем» время?
Мне очень хочется спросить у знающих людей, имеет ли право на существование моя формула для вычисления количества простых чисел на диапазон?

P.S.

Скорее всего, мне не нужно писать статьи, в которых я мало разбираюсь. Я не ожидал, что сообщество так на это отреагирует. Но я и не претендовал на то, что мое решение является единственно верным. Я являюсь дилетантом в этой области.
С какой целью я написал эту статью?
Я потратил время на изучение этого вопроса, и мне показалось что некоторым людям это может понравится. Для меня это было интересно, потому что это забавная задача. Но зачем на это тратят время математики? Я искренне не понимаю, какую реальную пользу несут исследование конкретно таких вопросов.

P.P.S.

После прочтения отзывов о статье, решил сделать выводы.

Скорее всего, мне так кажется, что существует более оптимальные варианты проверки числа на простоту

Как подсказали пользовательи dvserg drWhy и Pavel_The_Best это действительно так. Например, использую решето Эратосфена, коллекцию простых чисел можно собрать гораздо быстрее. Вот статьи которые можете почитать на эту тему: Алгоритм проверки на простоту за O (log N), Википедия, можно ознакомиться с трудами Сриниваса Рамануджан Айенгора

имеет ли право на существование моя формула для вычисления количества простых чисел на диапазон?

Нет

Решение проблемы Гольдбаха ничего не даст человечеству?

Мое мнение о том, что некоторые задачи математики бесполезны вызвало резко негативное отношение у большинства пользователей. Пользователи vvadzim Refridgerator bromzh Graph-in Refridgerator EimKR bfDeveloper и yea смогли меня переубедить в этом. Беру свои слова обратно.
С древних времен математики ищут истину, и их поиски часто приводят к выгодным последствиям для прогресса. Возможно, сама проблема и его решение не даст миру ничего здесь и сейчас, но именно выводы, сделанные во время поиска решения, могут быть полезными в долгосрочной перспективе.