Привет, Хабр.
В данной статье хотелось бы затронуть тему применения информационных технологий в Науках о Земле, а именно, в Гидрологии и Картографии. Под катом представлено описание алгоритма ранжирования водотоков и реализованного нами плагина для открытой геоинформационной системы QGIS.
Введение
В настоящее время важным аспектом гидрологических изысканий являются не только натурные наблюдения, но и камеральная работа с гидрологическими данными, в том числе и с использованием ГИС (геоинформационных систем). Однако, изучение пространственной структуры гидрологических систем может быть затруднено в виду большого объема данных. В таких случаях не обойтись без применения дополнительных инструментов, позволяющих специалисту автоматизировать процесс.
Важную роль при работе с цифровыми данными в целом и гидрологическими данными в частности играет визуализация — корректное и наглядное представление результатов анализа. Для отображения водотоков в классической картографии принят следующий способ: реки изображаются сплошной линией с постепенным (в зависимости, от количества впадающих в реку притоков) утолщением от истока к устью. Кроме того, для сегментов речной сети часто необходимо некоторое ранжирование по степени удаленности от истока. Информация такого рода важна не только с точки зрения визуализации, но и пригодна для более полного восприятия структуры данных, их пространственного распределения, и корректной последующей обработки.
Проиллюстрировать задачу ранжирования водотоков можно следующим образом (Рис. 1):

Рисунок 1. Задача ранжирования водотоков, цифрами обозначен присвоенный каждому сегменту речной сети атрибут совокупного количества впадающих притоков
Таким образом, каждому сегменту реки требуется сопоставить такое значение, которое бы показывало, сколько сегментов совокупно впадает в данный участок.
Современные ГИС, такие как ArcGIS или его open-source конкурент QGIS, имеют в своем арсенале инструменты работы с речными сетями. Однако, как правило, инструментам ранжирования рек требуется большое количество дополнительных вспомогательных материалов и, как нам кажется, лишних преобразований. Так, редко какой-либо существующий инструмент работы с речными сетями в ГИС может начинать свою работу без цифровой модели рельефа. Существенным недостатком, помимо сложной и многоступенчатой подготовки данных, является отсутствие возможности использовать уже подготовленные векторные слои с речной сетью для анализа, что ограничивает возможность применения в том числе цифровых основ из открытых источников (OpenStreetMap, Natural Earth, ВСЕГЕИ).
Конечно, присвоить значения атрибутов сегментам можно и вручную, однако подобный подход теряет актуальность, если водосборный бассейн включает в себя десятки тысяч сегментов.
Мы решили автоматизировать данную процедуру с помощью представления речной сети в математической форме — в виде графа и последующего применения алгоритмов обхода графов. Для упрощения работы пользователя с реализованным алгоритмом был написан плагин для геоинформационной системы QGIS — "Lines Ranking". Код распространяется свободно и доступен в репозитории QGIS, а также на GitHub.
Для работы плагина необходима версия QGIS >= 3.14, а также следующие зависимости: библиотеки языка программирования Python — networkx и pandas.
В качестве входных данных алгоритму подается векторный слой, состоящий из объектов с линейным типом геометрии (Line, MultiLine). Пользовательские атрибуты входного слоя сохраняются для результирующего слоя, поэтому могут быть значимыми.
- Не рекомендуется использовать для входного слоя поле с названием “fid”. На этапе соединения разрывов в речной сети использование встроенного модуля пакета GRASS — v.clean — приводит к непредвиденным исключениям в связи с тем, что такое название поля является системным.
Также обязательным входным параметром является точка (Start Point Coordinates), определяющая положение устья речной сети. Она может быть задана с карты, из файла, либо из слоя, загруженного в QGIS. Положение устья может быть примерным, в расчет берется ближайший к точке сегмент речной сети (замыкающий сегмент будущего графа).
Описать выполняемые алгоритмом задачи можно следующим образом: сопоставить каждому сегменту реки значение совокупно впадающих в него притоков, для каждого сегмента рассчитать количество притоков, а также удаленность крайней дальней точки сегмента от устья.
Описание алгоритма
В любой ГИС данные могут представляться в двух основных форматах: растровом и векторном. Растр — это матрица, где в каждом пикселе хранится некоторое значение параметра. В растровом формате в Науках о Земле часто представлены спутниковые снимки, поля реанализа, различные выходные слои из климатических моделей и др. Векторные данные представляются в виде простых геометрических объектов, таких как точки, линии и полигоны. Каждому объекту векторного формата может быть сопоставлена некоторая информация в виде атрибутов. Все описанные ниже действия мы будет производить именно над векторным слоем речной сети.
Результат работы алгоритма — векторный слой, в котором каждому объекту присвоены атрибуты, определяющие удаленность сегментов от устья реки и совокупное количество впадающих в данный сегмент притоков.
Предобработка входных данных
Отметим, что топология изначального векторного слоя может быть повреждена. Причиной может быть экспорт/импорт между различными ГИС, некорректное создание файла и т.д. Поврежденная топология слоя может выражаться в отсутствии соединений между объектами, т.е. образовании различных разрывов (Рис. 2), создании дополнительных замыканий, пересечений и т.п.
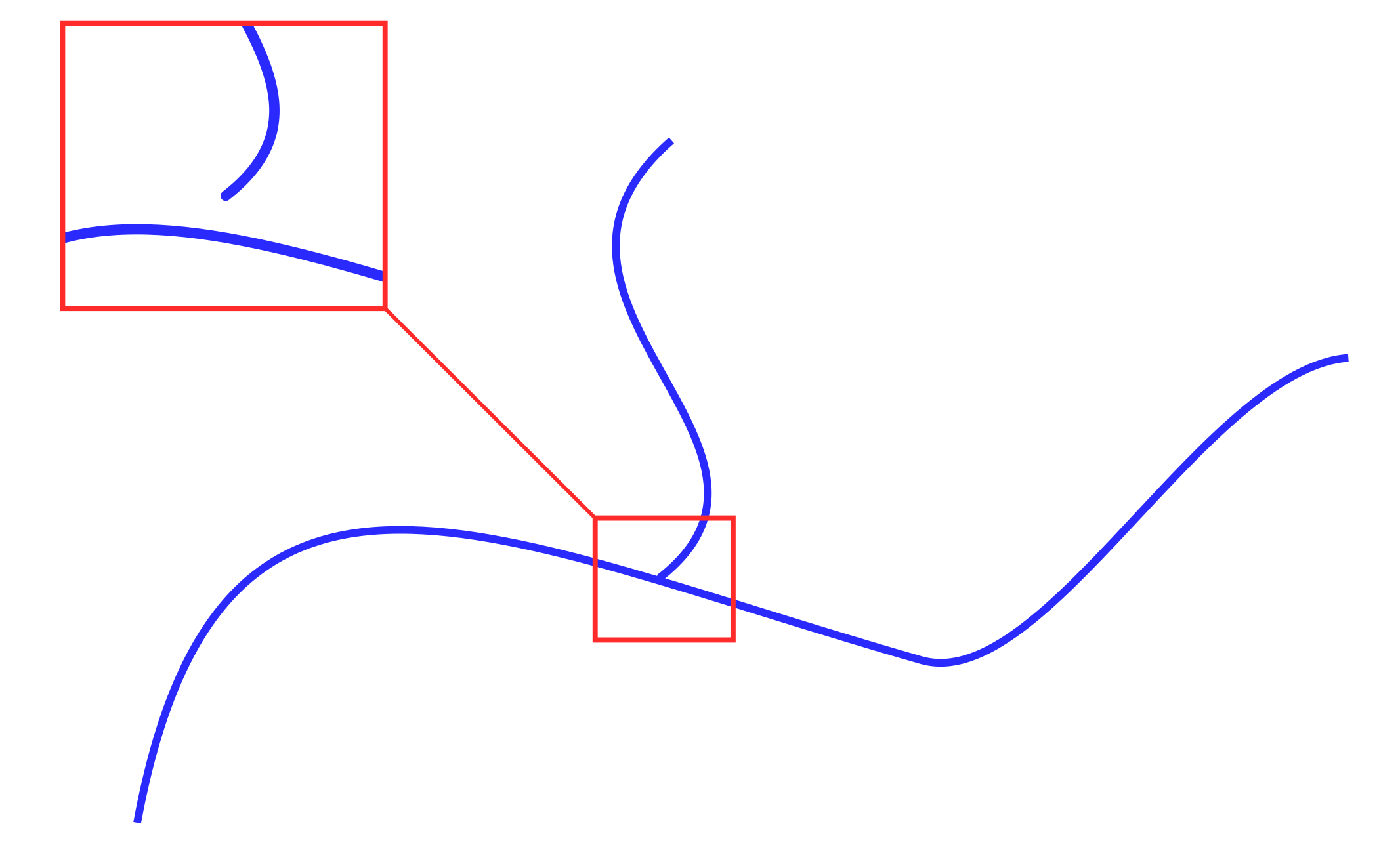
Рисунок 2. Нарушенная топология векторных объектов
Поэтому первым этапом предобработки является исправление топологии объектов: “подтянуть“ узлы, сделать исходный векторный слой консистентным. Для этого используются инструменты из панели анализа данных в QGIS – “Исправить геометрии” (fixgeometries — встроенный) и v.clean (из пакета GRASS).
После того как топология исправлена, слой разбивается на сегменты в точках соприкосновения и пересечения линий. Результат после разбиения проиллюстрирован ниже (Рис. 3).

Рисунок 3. Разбиение линейных объектов на сегменты
Таким образом, с помощью инструмента в QGIS "Разбить линиями" (splitwithlines — встроенный) мы делим исходный слой на сегменты.
Для каждого сегмента средствами QGIS мы рассчитываем протяженность и заносим данные в атрибутивную таблицу слоя (Рис. 4). Длина сегмента рассчитывается в соответствии с пользовательскими настройками проекта (Проект -> Свойства -> Общие -> Эллипсоид).

Рисунок 4. Расчет протяженности сегментов
После этого с помощью инструмента "Пересечение линий" (lineintersections — встроенный) мы получаем точечный векторный слой, где в таблице атрибутов занесена информация о пересечениях сегментов. Такую таблицу атрибутов можно интерпретировать как список смежности.
Схематично этапы предобработки представлены на следующих изображениях (Рис. 5).

Рисунок 5. Этапы предобработки векторного линейного слоя для представления его в виде графа
В результате предобработки формируется граф как математический объект Python библиотеки networkx. Таким образом, сегменты реки — это вершины графа, если сегменты связаны между собой (имеют пересечения), то между вершинами есть ребра.
Алгоритм ранжирования линейных объектов
После того, как граф сформирован, нам известно, из какой вершины следует начинать обход (точка впадения главной реки в водоем). В дальнейшем, будем называть эту вершину замыкающей, так как именно в неё "впадают" все остальные сегменты речной сети (вершины). Алгоритм мы разделили на несколько частей:
- Ранжирование вершин графа по удаленности от замыкающего сегмента с присваиванием атрибута "rank" (мера удаленности сегмента) и атрибута "offspring" (количество напрямую впадающих в данный сегмент участков речной сети);
- Обход графа с целью присваивания атрибута совокупно впадающих в данный участок сегментов водотоков "value" и атрибута "distance" (удаленности крайней точки сегмента от устья в метрах).
Оба этапа делятся на несколько блоков, однако, основная идея заключается в двуэтапной схеме присваивания атрибутов.
Присваивание атрибутов "rank" и "offspring"
Переходим к первому этапу обхода графа — ранжирование вершин по степени удаленности от замыкающей. Изначально, мы планировали осуществлять присваивание атрибута "rank" при помощи итеративного обхода в ширину. Таким образом, начиная от замыкающей вершины, мы бы на каждом шаге отдалялись все дальше и дальше, и вместе с этим, присваивали бы атрибут. Но в таком случае может возникнуть следующий конфликт (Анимация ниже)

И какой ранг нам присвоить данному сегменту? Вообще, для такого алгоритма присваивания атрибутов могут возникать и другие проблемы, но мы привели одну из ключевых.
Предложенное решение: можно однозначно определить ранги для какой-то части речной сети (главной реки), и ранжировать сегменты опираясь уже на эту информацию. Данный подход можно проиллюстрировать следующей картинкой (Рис. 6).

Рисунок 6. Разрешение конфликта путем введения опорного маршрута в графе
Таким образом, подграфы могут примыкать к опорному маршруту только через 1 ребро, остальные ребра — исключаются.
Здесь возникает следующая проблема — как найти такой маршрут? — Будем считать, что кратчайший маршрут между двумя наиболее удаленными друг от друга вершинами в графе, одна из которых является замыкающей, — опорный маршрут (скоро мы добавим обновление, чтобы пользователь мог вручную задать такой маршрут, если у него есть априорные знания какая река является главной, но при отсутствии такой информации опорный маршрут определяется именно таким образом). Такой маршрут можно получить при помощи алгоритма A* (A-star), но данный алгоритм работает на взвешенном графе, а на ребрах нашего пока никаких весов нет. Но мы можем задать веса ребрам графа на основе длин сегментов (мы рассчитали их ранее).
1) Присваивание весов ребрам графа на основе протяженностей сегментов. Одновременно с этим этапом происходит выделение одной компоненты связности в графе. Перемещение по графу осуществляется при помощи поиска в ширину. Присваивание весов можно продемонстрировать следующим рисунком (Рис. 7)

Рисунок 7. Присваивание весов ребрам графа
Таким образом, каждая вершина графа имеет атрибут "length", который обозначает протяженность данного сегмента реки в метрах. Мы же переносим значения атрибутов с вершин графа на ребра итеративно, начиная обход графа в ширину из замыкающей вершины.
Данную задачу выполняет следующая функция
Input:
- G — исходный граф
- start — вершина, из которой требуется начинать обход
- dataframe — pandas датафрейм, в котором присутствуют 2 столбца: id_field (идентификатор сегмента/вершины) и 'length' (длина данного сегмента)
- id_field — поле в dataframe, из которого требуется сопоставлять идентификаторы с вершинами графа
- main_id — индекс, которым обозначается главная река в речной сети (по умолчанию = None)
Output:
- На исходном графе ребрам присваиваются веса таким образом, что если начальная вершина 1, соседние с ней узлы графа: 2 и 3, где значение атрибута 'length' для сегментов 1 — 10, 2 — 15, 3 — 20. В результате ребрам будет присвоены значения следующим образом: (1, 2) и (2, 1) — 15; (1, 3) и (3, 1) — 20 и т.д.
- last_vertex — одна из самых удаленных вершин от начальной в графе (данная вершина необходима для нахождения кратчайшего пути между двумя самыми удаленными сегментами в речной сети)
# Function for assigning weights to graph edges
def distance_attr(G, start, dataframe, id_field, main_id = None):
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source=start))
# One of the most remote vertices in the graph (this will be necessary for A*)
last_vertex = vert_list[-1][-1][0]
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
dist_vertex = int(dataframe['length'][dataframe[id_field] == vertex])
# Assign the segment length value as a vertex attribute
attrs = {vertex: {'component' : 1, 'size' : dist_vertex}}
nx.set_node_attributes(G, attrs)
for n in neighbors:
# If the main index value is not set
if main_id == None:
# Assign weights to the edges of the graph
# The length of the section in meters (int)
dist_n = int(dataframe['length'][dataframe[id_field] == n])
# Otherwise we are dealing with a complex composite index
else:
# If the vertex we are at is part of the main river
if vertex.split(':')[0] == main_id:
# And at the same time, the vertex that we "look" at from the vertex "vertex" also, then
if n.split(':')[0] == main_id:
# The weight value must be zero
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
# Assign attributes to the nodes of the graph
attrs = {n: {'component' : 1, 'size' : dist_n}}
nx.set_node_attributes(G, attrs)
# Look at the surroundings of the vertex where we are located
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
offspring = offspring[0][1]
# If the weight value was not assigned, we assign it
for n in offspring:
if len(G.get_edge_data(vertex, n)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
elif len(G.get_edge_data(n, vertex)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
for vertex in list(G.nodes()):
# If the graph is incompletely connected, then we delete the elements that we can't get to
if G.nodes[vertex].get('component') == None:
G.remove_node(vertex)
else:
pass
return(last_vertex)
# The application of the algorithm
last_vertex = distance_attr(G, '7126:23', dataframe, id_field = 'id', main_id = '7126')2) A* (А-star) поиск кратчайшего пути на взвешенном графе между замыкающей и одной из самых удаленных вершин (сегмента в речной сети). Данный самый короткий маршрут между двумя самыми удаленными вершинами в графе мы назовем "опорным";
3) Ранжирование по удаленности всех вершин в опорном маршруте. Вершине, из которой мы начинаем обход, присваивается значение ранга 1, следующей вершине — 2, далее — 3 и т.д.
4) Итеративный обход графа с началом в вершинах опорного маршрута с изоляцией рассматриваемых подграфов. Если одна из ветвей графа уже имеет соединение с вершинами опорного маршрута, то ребра, связывающие подграф с другими опорными вершинами, удаляются.
Исходный код можно увидеть ниже
Input:
- G — граф с присвоенными весами на ребрах
- start — вершина, из которой требуется начинать обход
- last_vertex — одна из самых удаленных вершин от начальной в графе
Output:
- Каждой вершине графа присваивается значение его ранга в речной сети. Ранг 1 имеет сегмент реки, который является замыкающим в речной сети. Ранг 2 имеют притоки, которые впадают в сегмент ранга 1. Ранг 3 имеют притоки, которые впадают в сегмент ранга 2 и т.д. После того, как все вершины графа имеют значение атрибута 'rank', производится подсчет потомков для каждой вершины 'offspring'. Значение атрибута 'offspring' можно интерпретировать как 'количество сегментов, которое впадает в данный сегмент речной сети'.
# Function for assigning 'rank' and 'offspring' attributes to graph vertices
def rank_set(G, start, last_vertex):
# Traversing a graph with attribute assignment
# G --- graph as a networkx object
# vertex --- vertex from which the graph search begins
# kernel_path --- list of vertexes that are part of the main path that the search is being built from
def bfs_attributes(G, vertex, kernel_path):
# Creating a copy of the graph
G_copy = G.copy()
# Deleting all edges that are associated with the reference vertexes
for kernel_vertex in kernel_path:
# Leaving the reference vertex from which we start the crawl
if kernel_vertex == vertex:
pass
else:
# For all other vertexes, we delete edges
kernel_n = list(nx.bfs_successors(G_copy, source = kernel_vertex, depth_limit = 1))
kernel_n = kernel_n[0][1]
for i in kernel_n:
try:
G_copy.remove_edge(i, kernel_vertex)
except Exception:
pass
# The obtained subgraph is isolated from all reference vertices, except the one
# from which the search begins at this iteration
# Breadth-first search
all_neighbors = list(nx.bfs_successors(G_copy, source = vertex))
# Attention!
# Labels are not assigned on an isolated subgraph, but on the source graph
for component in all_neighbors:
v = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Value of the 'rank' attribute in the considering vertex
att = G.nodes[v].get('rank')
if att != None:
# The value of the attribute to be assigned to neighboring vertices
att_number = att + 1
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = v, depth_limit = 1))
first_n = first_n[0][1]
# Assigning ranks to vertices
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
current_i_rank = G.nodes[i].get('rank')
# If the rank value has not yet been assigned, then assign it
if current_i_rank == None:
attrs = {i: {'rank': att_number}}
nx.set_node_attributes(G, attrs)
# If the rank in this node is already assigned
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(v, i)
else:
pass
# Additional "search"
for neighbor in neighbors:
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = neighbor, depth_limit = 1))
first_n = first_n[0][1]
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(neighbor, i)
else:
pass
# Finding the shortest path A* - building a route around which we will build the next searchs
a_path = list(nx.astar_path(G, source = start, target = last_vertex, weight = 'weight'))
##############################
# Route validation block #
##############################
true_a_path = []
for index, V in enumerate(a_path):
if index == 0:
true_a_path.append(V)
elif index == (len(a_path) - 1):
true_a_path.append(V)
else:
# Previous and next vertices for the reference path (a_path)
V_prev = a_path[index - 1]
V_next = a_path[index + 1]
# Which vertexes are adjacent to this one
V_prev_neighborhood = list(nx.bfs_successors(G, source = V_prev, depth_limit = 1))
V_prev_neighborhood = V_prev_neighborhood[0][1]
V_next_neighborhood = list(nx.bfs_successors(G, source = V_next, depth_limit = 1))
V_next_neighborhood = V_next_neighborhood[0][1]
# If the next and previous vertices are connected to each other without an intermediary
# in the form of vertex V, then vertex V is excluded from the reference path
if any(V_next == VPREV for VPREV in V_prev_neighborhood):
if any(V_prev == VNEXT for VNEXT in V_next_neighborhood):
pass
else:
true_a_path.append(V)
else:
true_a_path.append(V)
##############################
# Route validation block #
##############################
# Verification completed
a_path = true_a_path
RANK = 1
for v in a_path:
# Assign the attribute rank value - 1 to the starting vertex. The further away, the greater the value
attrs = {v: {'rank' : RANK}}
nx.set_node_attributes(G, attrs)
RANK += 1
# The main route is ready, then we will iteratively move from each node
for index, vertex in enumerate(a_path):
# Starting vertex
if index == 0:
next_vertex = a_path[index + 1]
# Disconnect vertices
G.remove_edge(vertex, next_vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(vertex, next_vertex)
# Finishing vertex
elif index == (len(a_path) - 1):
prev_vertex = a_path[index - 1]
# Disconnect vertices
G.remove_edge(prev_vertex, vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(prev_vertex, vertex)
# Vertices that are not the first or last in the reference path
else:
prev_vertex = a_path[index - 1]
next_vertex = a_path[index + 1]
# Disconnect vertices
# Previous with current vertex
try:
G.remove_edge(prev_vertex, vertex)
except Exception:
pass
# Current with next vertex
try:
G.remove_edge(vertex, next_vertex)
except Exception:
pass
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
try:
G.add_edge(prev_vertex, vertex)
G.add_edge(vertex, next_vertex)
except Exception:
pass
# Attribute assignment block - number of descendants
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Adding an attribute - the number of descendants of this vertex
n_offspring = len(neighbors)
attrs = {vertex: {'offspring' : n_offspring}}
nx.set_node_attributes(G, attrs)Демонстрацию описанных действий можно увидеть на анимации:

Таким образом, опорный маршрут можно рассматривать как главную реку в речной сети, когда все остальные сегменты являются притоками для главной. Описанный выше алгоритм в полной мере соответствует данным рассуждениям.
Более того, подобный подход позволяет добиться однозначности при ранжировании рек в "сложных" местах, таких как дельта, где некоторые рукава сначала отходят от главной реки, а затем, набирая новые притоки, впадают в главную реку снова.
Присваивание атрибутов "value" и "distance"
Итак, на графе всем вершинам присвоены значения атрибутов "rank" и "offspring". Дальнейшие рассуждения можно свести к следующему.
Если вершина графа не имеет потомков, то это значит, что ни один приток в данный сегмент речной сети не впадает, следовательно, данной вершине требуется присвоить значение "value" — 1. Затем, для каждого узла, у которого имеются потомки со значением "value", равному 1, необходимо сложить значения "value" у потомков (ранг потомков всегда на 1 меньше, чем ранг рассматриваемой вершины) и присвоить полученное число как атрибут вершины "value". Затем, данная процедура повторяется ровно столько раз, сколько рангов присутствует в графе.
Таким образом, мы итеративно продвигаемся к начальной вершине.
Input:
- G — граф с присвоенными значениями атрибутов 'rank' и 'offspring'
- start — вершина, из которой требуется начинать обход
Output:
- Каждой вершине графа G присваивается значение атрибута 'value'. Значение данного атрибута можно интерпретировать как 'количество совокупно впадающих притоков в данную часть речной сети'. Также присваивается атрибут 'distance', который означает расстояние, которое потребуется преодолеть, чтобы достичь устья реки из данного сегмента.
# Function for determining the order of river segments similar to the Shreve method
# In addition, the "distance" attribute is assigned
def set_values(G, start, considering_rank, vert_list):
# For each vertex in the list
for vertex in vert_list:
# If value has already been assigned, then skip it
if G.nodes[vertex].get('value') == 1:
pass
else:
# Defining descendants
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
# We use only the nearest neighbors to this vertex (first descendants)
offspring = offspring[0][1]
# The cycle of determining the values at the vertices of a descendant
last_values = []
for child in offspring:
# We only need descendants whose rank value is greater than that of the vertex
if G.nodes[child].get('rank') > considering_rank:
if G.nodes[child].get('value') != None:
last_values.append(G.nodes[child].get('value'))
else:
pass
else:
pass
last_values = np.array(last_values)
sum_values = np.sum(last_values)
# If the amount is not equal to 0, the attribute is assigned
if sum_values != 0:
attrs = {vertex: {'value' : sum_values}}
nx.set_node_attributes(G, attrs)
else:
pass
# Function for iteratively assigning the value attribute
def iter_set_values(G, start):
# Vertices and corresponding attribute values
ranks_list = []
vertices_list = []
offspring_list = []
for vertex in list(G.nodes()):
ranks_list.append(G.nodes[vertex].get('rank'))
vertices_list.append(vertex)
att_offspring = G.nodes[vertex].get('offspring')
if att_offspring == None:
offspring_list.append(0)
else:
offspring_list.append(att_offspring)
# Largest rank value in a graph
max_rank = max(ranks_list)
# Creating pandas dataframe
df = pd.DataFrame({'ranks': ranks_list,
'vertices': vertices_list,
'offspring': offspring_list})
# We assign value = 1 to all vertices of the graph that have no offspring
value_1_list = list(df['vertices'][df['offspring'] == 0])
for vertex in value_1_list:
attrs = {vertex: {'value' : 1}}
nx.set_node_attributes(G, attrs)
# For each rank, we begin to assign attributes
for considering_rank in range(max_rank, 0, -1):
# List of vertices of suitable rank
vert_list = list(df['vertices'][df['ranks'] == considering_rank])
set_values(G, start, considering_rank, vert_list)
# Assigning the "distance" attribute to the graph vertices
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# If we are at the closing vertex
if vertex == start:
# Length of this segment
att_vertex_size = G.nodes[vertex].get('size')
# Adding the value of the distance attribute
attrs = {vertex: {'distance' : att_vertex_size}}
nx.set_node_attributes(G, attrs)
else:
pass
vertex_distance = G.nodes[vertex].get('distance')
# For each neighbor, we assign an attribute
for i in neighbors:
# Adding the value of the distance attribute
i_size = G.nodes[i].get('size')
attrs = {i: {'distance' : (vertex_distance + i_size)}}
nx.set_node_attributes(G, attrs) 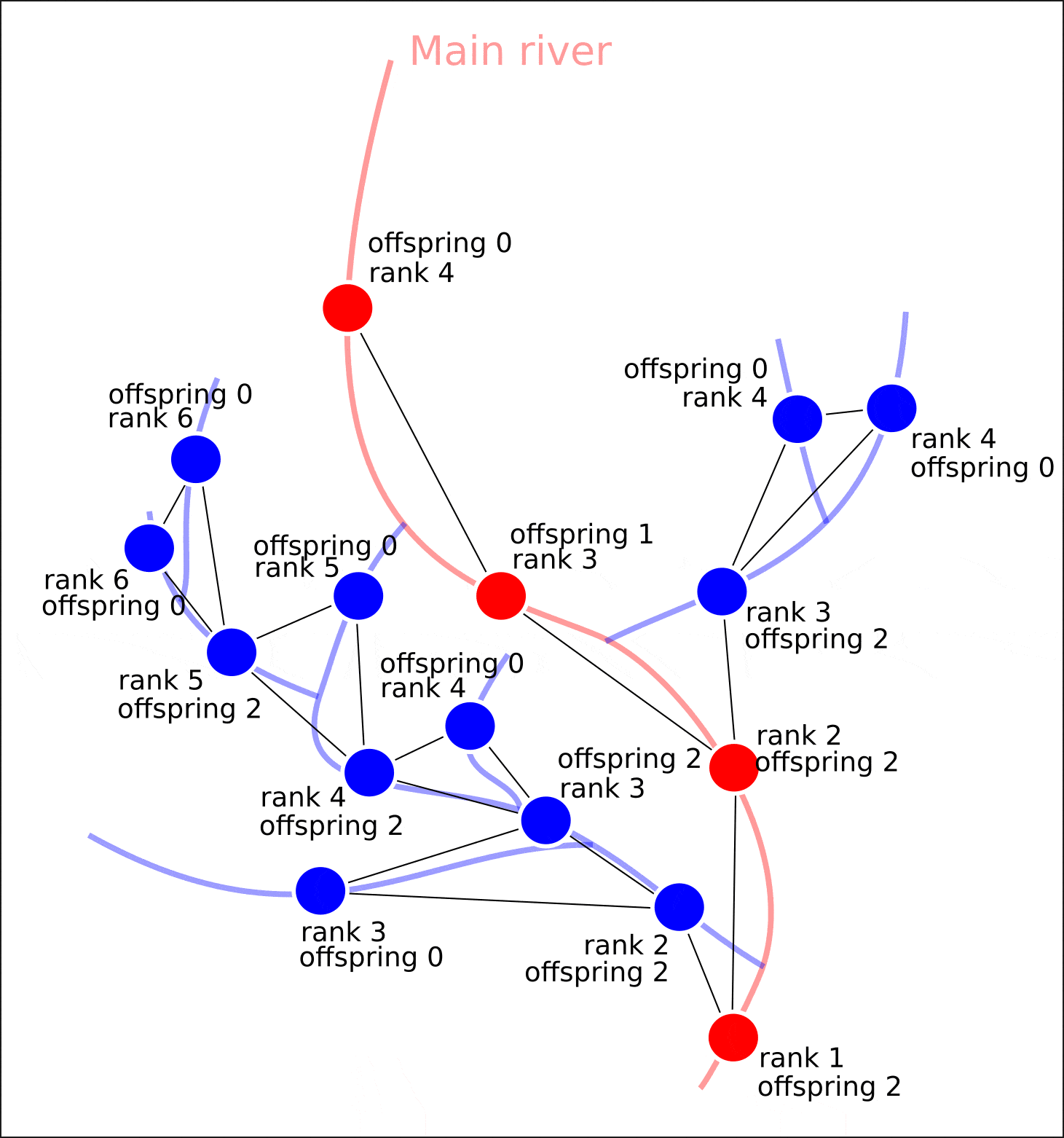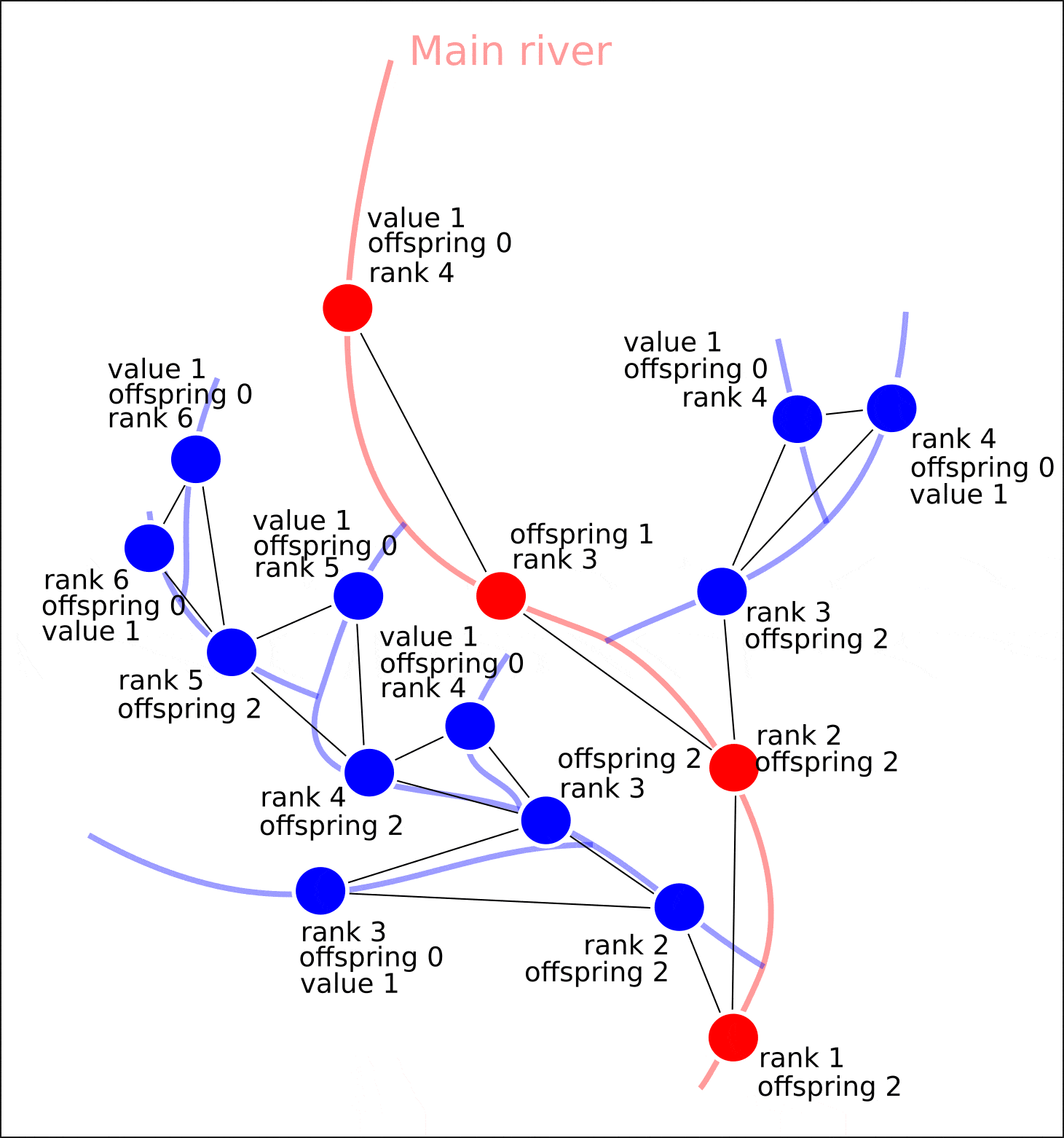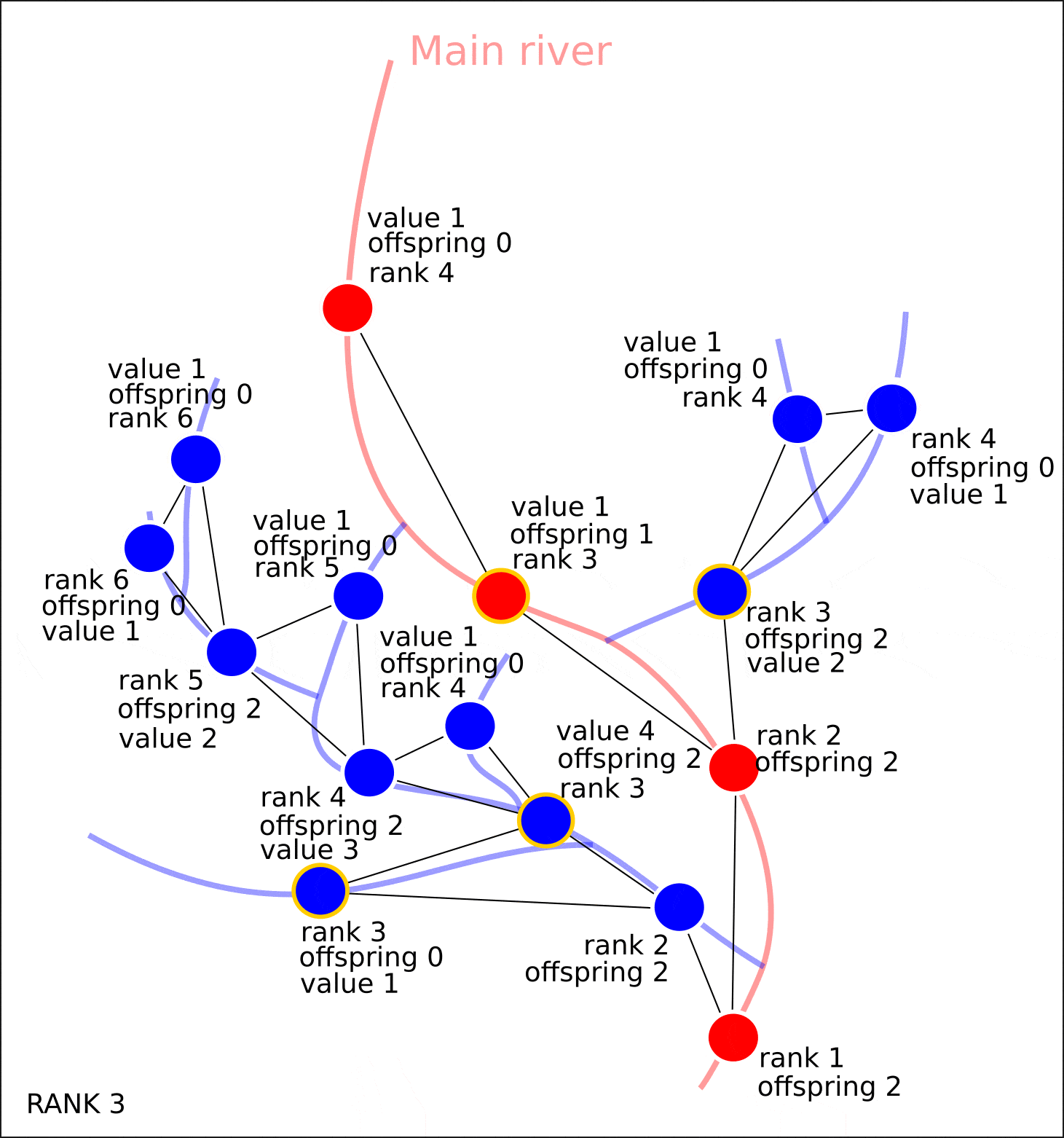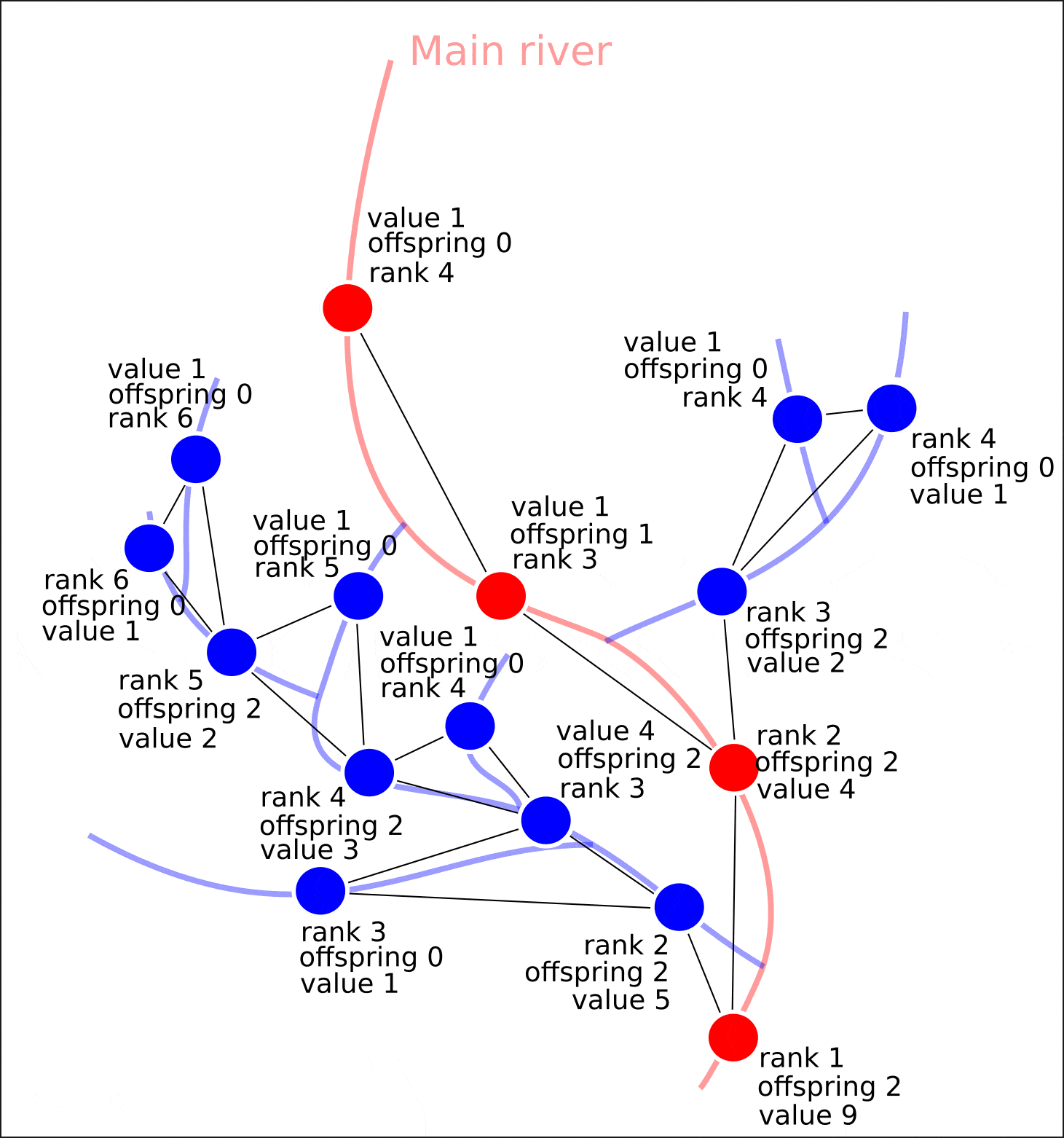
Одновременно с присваиванием вершинам графа атрибута "value", производится присваивание атрибута "distance", который характеризует удаленность сегментов от устья не количеством сегментов, которое необходимо преодолеть, чтобы достичь замыкающего, а расстояние в метрах, которое необходимо будет преодолеть, чтобы достичь устья реки.
Результат использования алгоритма можно увидеть на рисунке 8. Удаленность сегментов речной сети показана на основе атрибута "rank" и совокупное количество притоков показано на основе атрибута "value".

Рисунок 8. Результаты использования алгоритма (данные OpenStreetMap, Удаленность сегментов речной сети показана на основе атрибута "rank", Совокупное количество впадающих притоков- на основе атрибута "value")
Заключение
Как видно, представленный алгоритм позволяет ранжировать реки без использования дополнительной информации о рельефе территории. Необходимым входным параметром за исключением основного слоя речной сети является положение замыкающего сегмента (место впадения реки в водоем), которое можно указать точкой.
Таким образом, при минимальном количестве требуемых входных данных с использованием реализованного алгоритма представляется возможность получить структурированную производную информацию, характеризующую элементы речного бассейна.
Открытой реализацией алгоритма на языке Python, а также встраиваемым плагином для QGIS может воспользоваться любой желающий. Вся обработка осуществляется одним потоком, у пользователя нет необходимости запускать все описанные функции по отдельности.
Мы будем рады ответить на ваши вопросы и увидеть ваши комментарии.
Репозиторий с исходным кодом:
Над алгоритмом и статьей работали Михаил Сарафанов, Юлия Борисова.


Germanjon
Проверяли ли работу алгоритма, в случае если река уходит под поверхность земли на некоторое расстояние?
Не возникает ли проблема в случае больших островов или редких случаях бифуркации рек? Или в случае разбиения реки на протоки (например, в дельте)
Dreamlone Автор
Мы пробовали алгоритм на нескольких речных сетях (данные OpenStreetMap), из крупных рек: Урал и Обь. Постараюсь ответить по пунктам:
«Проверяли ли работу алгоритма, в случае если река уходит под поверхность земли на некоторое расстояние?» — Нет, такой ситуации мы не встречали при тестировании плагина. Но если вдруг в линейном векторном слое будет присутствовать разрыв, то алгоритм дальше этого разрыва не пойдет присваивать ранги. Так что если имеется разрыв в речной сети, и Вы точно знаете, что сегменты рядом с разрывом в действительности связаны, а не изолированы друг от друга, то можно исправить векторный слой вручную — соединить их. В таком случае алгоритм отработает как требуется.
«Не возникает ли проблема в случае больших островов или редких случаях бифуркации рек?» — Острова в линейном векторном слое — вещь довольная специфическая, они могут возникнуть, если например, мы имели не только векторный линейный слой с реками, а еще и полигональный векторный слой с водохранилищами, озерами и др. В таком случае эти площадные объекты действительно являются частью речной сети и если их не использовать, то речная сеть получится с разрывами (должно было быть водохранилище на этом месте, а его мы отбросили, и водотока в слое на этом месте тоже не оказывается). Выход довольно простой — переводим векторный полигональный слой в линейный (инструмент в QGIS Полигон в линии) и объединяем с изначальным линейным слоем с реками. Вот в таком слое могут быть ситуации, когда алгоритм считает за 2 разные реки берега одного водохранилища. Но с этим ничего поделать мы не смогли, исправлять данные вещи насильно при применении алгоритма мы не пытались, потому что вполне возможен случай, когда река просто разделяется на несколько рукавов, а потом снова сходится и никакие полигональные водные объекты тут не при чем. А вот с бифуркацией да, есть загвоздка. Так как определяющим фактором является местоположение точки впадения реки в водоём, то алгоритм считает, что именно в эту указанную пользователем точку, вся речная сеть и стекает. В таком случае алгоритм будет считать, что отошедшая ранее ветвь является притоком. Как-то отсеять это алгоритм не сможет. Тогда проще будет вручную отделить рукав от речной сети, а затем запустить алгоритм для каждой из частей речной сети отдельно — потом слои можно будет вновь соединить.
«Или в случае разбиения реки на протоки (например, в дельте)» — На рисунке 8 и в анимациях как раз приведен пример такого разбиения. Проблем возникнуть не должно, так как мы в любом случае опираемся на главную реку (назовем её опорным маршрутом в графе), и уже от неё начинаем обходить граф и присваивать ранги. Введение опорного маршрута как раз помогло нам адекватно обрабатывать подобные случаи.