Привет, Хабр! Представляю вашему вниманию перевод статьи "Python?0????????????????????(1. ???)".
Например, у нас есть следующий набор данных (дата сет): погода, температура, влажность, ветер, игра в гольф. В зависимости от погоды и остального, мы ходили (?) или не ходили (?) играть в гольф. Предположим, что у нас есть 14 сложившихся вариантов.
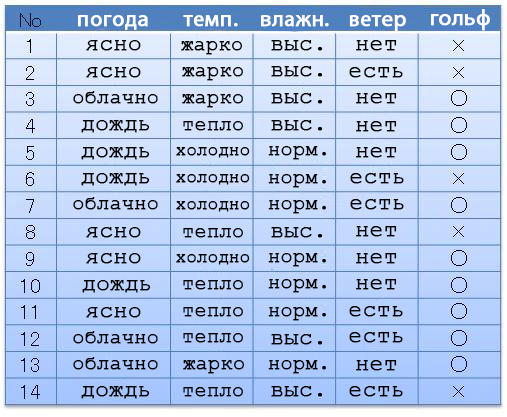
Из этих данных мы можем составить структуру данных, показывающую, в каких случаях мы шли на гольф. Такая структура из-за своей ветвистой формы называется Decision Tree.
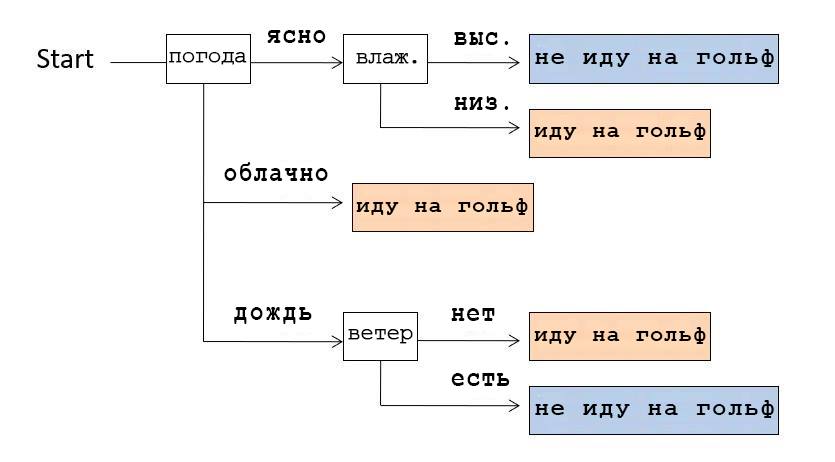
Например, если посмотреть на Decision Tree, изображенный на картинке выше, мы поймем, что сначала проверяли погоду. Если было ясно, мы проверяли влажность: если она высокая, то не шли играть в гольф, если низкая — шли. А если погода была облачная, то шли играть в гольф вне зависимости от других условий.
Существуют алгоритмы, которые создают такие Decision Tree автоматически, на основе имеющихся данных. В этой статье мы будем использовать алгоритм ID3 на Python.
Эта статья — первая из серии. Следующие статьи:
(Прим. переводчика: “если вас заинтересует продолжение, пожалуйста, сообщите нам в в комментариях”.)
Генерация Decision Tree связана с машинным обучением с учителем и классификацией. Классификация в машинном обучении — способ, позволяющий создать модель, ведущую к правильному ответу, на основе обучении на дата сете с правильными ответами и ведущими к ним данными. Глубокое обучение (Deep Learning), которое в последние годы очень популярно, особенно в сфере распознавания изображений, тоже является частью машинного обучения на основе классификационного метода. Разница Deep Learning и Decision Tree в том, приводится ли конечный результат к форме, при которой человек понимает принципы генерации конечной структуры данных. Особенность Deep Learning — мы получаем конечный результат, но не понимаем принцип его генерации. В отличие от Deep Learning, принцип построения Decision Tree прост для понимания человеком, что также является его важной особенностью.
Эта особенность Decision Tree хороша не только для машинного обучения, но и дата майнинга, где также важно понимание данных пользователем.
ID3 — алгоритм генерации Decision Tree, разработанный в 1986 году Россом Куинланом. У него есть две важные особенности:
Алгоритм С4.5, который является более продвинутой версией ID3, может использовать численные данные, но так как базовая идея такая же, в этой серии статей, мы, для начала, будет использовать ID3.
Программа, которую я описал ниже, я проверил и запустил в следующих условиях:
Для начала, скопируем программу в Jupyter Notebook и запустим.
Если запустить вышеописанную программу, наш Decision Tree будет представлен в виде символьной таблицы, как показано ниже.
Последний массив в дата сете d — это атрибут класса (массив данных, который хотим классифицировать).
Например, если поменять местами массивы “Гольф” и “Ветер”, как указано на примере выше, получится следующий результат:
По сути, мы создаем правило, при котором сообщаем программе, что разветвляться нужно сначала по наличию и отсутствию ветра и по тому, идем играть в гольф или нет.
Спасибо за прочтение!
Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?
1.1 Что такое Decision Tree?
1.1.1 Пример Decision Tree
Например, у нас есть следующий набор данных (дата сет): погода, температура, влажность, ветер, игра в гольф. В зависимости от погоды и остального, мы ходили (?) или не ходили (?) играть в гольф. Предположим, что у нас есть 14 сложившихся вариантов.

Из этих данных мы можем составить структуру данных, показывающую, в каких случаях мы шли на гольф. Такая структура из-за своей ветвистой формы называется Decision Tree.

Например, если посмотреть на Decision Tree, изображенный на картинке выше, мы поймем, что сначала проверяли погоду. Если было ясно, мы проверяли влажность: если она высокая, то не шли играть в гольф, если низкая — шли. А если погода была облачная, то шли играть в гольф вне зависимости от других условий.
1.1.2 Об этой статье
Существуют алгоритмы, которые создают такие Decision Tree автоматически, на основе имеющихся данных. В этой статье мы будем использовать алгоритм ID3 на Python.
Эта статья — первая из серии. Следующие статьи:
(Прим. переводчика: “если вас заинтересует продолжение, пожалуйста, сообщите нам в в комментариях”.)
- Основы программирования на Python
- Необходимые основы библиотеки для анализа данных Pandas
- Основы структуры данных (в случае с Decision Tree)
- Основы информационной энтропии
- Учим алгоритм для генерации Decision Tree
1.1.3 Немного о Decision Tree
Генерация Decision Tree связана с машинным обучением с учителем и классификацией. Классификация в машинном обучении — способ, позволяющий создать модель, ведущую к правильному ответу, на основе обучении на дата сете с правильными ответами и ведущими к ним данными. Глубокое обучение (Deep Learning), которое в последние годы очень популярно, особенно в сфере распознавания изображений, тоже является частью машинного обучения на основе классификационного метода. Разница Deep Learning и Decision Tree в том, приводится ли конечный результат к форме, при которой человек понимает принципы генерации конечной структуры данных. Особенность Deep Learning — мы получаем конечный результат, но не понимаем принцип его генерации. В отличие от Deep Learning, принцип построения Decision Tree прост для понимания человеком, что также является его важной особенностью.
Эта особенность Decision Tree хороша не только для машинного обучения, но и дата майнинга, где также важно понимание данных пользователем.
1.2 Об алгоритме ID3
ID3 — алгоритм генерации Decision Tree, разработанный в 1986 году Россом Куинланом. У него есть две важные особенности:
- Категориальные данные. Это данные по типу нашего примера выше (пойду на гольф или не пойду), данные с определенным категорийным ярлыком. ID3 не может использовать численные данные.
- Информационная энтропия — индикатор, который указывает на последовательность данных с наименьшей дисперсией свойств класса значений.
1.2.1 Об использовании численных данных
Алгоритм С4.5, который является более продвинутой версией ID3, может использовать численные данные, но так как базовая идея такая же, в этой серии статей, мы, для начала, будет использовать ID3.
1.3 Среда разработки
Программа, которую я описал ниже, я проверил и запустил в следующих условиях:
- Jupyter Notebooks (с использованием Azure Notebooks)
- Python 3.6
- Библиотеки: math, pandas, functools (не использовал scikit-learn, tensorflow и т.д.)
1.4 Пример программы
1.4.1 Собственно, программа
Для начала, скопируем программу в Jupyter Notebook и запустим.
import math
import pandas as pd
from functools import reduce
# Дата сет
d = {
"Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"],
"Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"],
"Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"],
"Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"],
# Последний массив - это наша целевая переменная, показывающая результат,
# основывающийся на предыдущих данных.
"Гольф":["?","?","0","0","0","?","0","?","0","0","0","0","0","?"],
}
df0 = pd.DataFrame(d)
# Лямбда-выражение для распределения значений, аргумент - pandas.Series,
# возвращаемое значение - массив с количеством каждого из значений
# Из вводных данных s с помощью value_counts() находим частоту каждого из значений,
# и пока в нашем словаре есть элементы, будет работать цикл, запускаемый items().
# Чтобы выходные данные не менялись с каждым запуском цикла, мы используем sorted,
# который меняет порядок от большего к меньшему
# В итоге, генерируется массив, содержащий строку из следующих компонентов: ключ (k) и значение (v).
cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())]
# Структура данных Decision Tree
tree = {
# name: Название этого нода (узла)
"name":"decision tree "+df0.columns[-1]+" "+str(cstr(df0.iloc[:,-1])),
# df: Данные, связанные с этим нодом (узлом)
"df":df0,
# edges: Список ребер (ветвей), выходящих из этого узла,
# или пустой массив, если ниже нет листового узла.
"edges":[],
}
# Генерацию дерева, у узлов которого могут быть ветви, сохраняем в open
open = [tree]
# Лямба-выражение для вычесления энтропии.
# Аргумент - pandas.Series?возвращаемое значение - число энтропии
entropy = lambda s:-reduce(lambda x,y:x+y,map(lambda x:(x/len(s))*math.log2(x/len(s)),s.value_counts()))
# Зацикливаем, пока open не станет пустым
while(len(open)!=0):
# Вытаскиваем из массива open первый элемент,
# и вытаскиваем данные, хранящиеся в этом узле
n = open.pop(0)
df_n = n["df"]
# В случае, если энтропия этого узла равна 0, мы больше не можем вырастить из него новые ветви
# поэтому прекращаем ветвление от этого узла
if 0==entropy(df_n.iloc[:,-1]):
continue
# Создаем переменную, в которую будем сохранять список значений атрибута с возможностью разветвления
attrs = {}
# Исследуем все атрибуты, кроме последнего столбца класса атрибутов
for attr in df_n.columns[:-1]:
# Создаем переменную, которая хранит значение энтропии при ветвлении с этим атрибутом,
# данные после разветвления и значение атрибута, который разветвляется.
attrs[attr] = {"entropy":0,"dfs":[],"values":[]}
# Исследуем все возможные значения этого атрибута.
# Кроме того, sorted предназначен для предотвращения изменения порядка массива,
# из которого были удалены повторяющиеся значения атрибутов, при каждом его выполнении.
for value in sorted(set(df_n[attr])):
# Фильтруем данные по значению атрибута
df_m = df_n.query(attr+"=='"+value+"'")
# Высчитываем энтропию, данные и значения сохрнаяем
attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0]
attrs[attr]["dfs"] += [df_m]
attrs[attr]["values"] += [value]
pass
pass
# Если не осталось ни одного атрибута, значение которого можно разделить,
# прерываем исследование этого узла.
if len(attrs)==0:
continue
# Получаем атрибут с наименьшим значением энтропии
attr = min(attrs,key=lambda x:attrs[x]["entropy"])
# Добавляем каждое значение разветвленного атрибута
# и данные, полученные после разветвления, в наше дерево и в open.
for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]):
m = {"name":attr+"="+v,"edges":[],"df":d.drop(columns=attr)}
n["edges"].append(m)
open.append(m)
pass
# Выводим дата сет
print(df0,"\n-------------")
# Метод преобразования дерева в символы, аргуметы - tree:структура данных древа,
# indent:присоединяймый к дочернему узлу indent,
# Возвращаемое значение - символьное представление древа.
# Этот метод вызывается рекурсивно для преобразования всех данных в дереве в символы.
def tstr(tree,indent=""):
# Создаем символьное представление этого узла.
# Если этот узел является листовым узлом (количество элементов в массиве ребер равно 0),
# частотное распределение последнего столбца данных df, связанных с деревом, преобразуется в символы.
s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n"
# Зацикливаем все ветви этого узла.
for e in tree["edges"]:
# Добавляем символьное представление дочернего узла к символьному представлению родительского узла.
# Добавляем еще больше символов к indent этого узла.
s += tstr(e,indent+" ")
pass
return s
# Выводим древо в его символьном представлении.
print(tstr(tree))1.4.2 Результат
Если запустить вышеописанную программу, наш Decision Tree будет представлен в виде символьной таблицы, как показано ниже.
decision tree Гольф ['?:5', '0:9']
Погода=Ясно
Влажность=Обычная['0:2']
Влажность=Высокая['?:3']
Погода=Облачно['0:4']
Погода=Дождь
Ветер=Есть['?:2']
Ветер=Нет['0:3']
1.4.3 Меняем атрибуты (массивы данных), которые хотим исследовать
Последний массив в дата сете d — это атрибут класса (массив данных, который хотим классифицировать).
d = {
"Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"],
"Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"],
"Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"],
"Гольф":["?","?","0","0","0","?","0","?","0","0","0","0","0","?"],}
# Последний массив - это наша целевая переменная, показывающая результат, основывающийся на предыдущих данных.
"Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"],
}Например, если поменять местами массивы “Гольф” и “Ветер”, как указано на примере выше, получится следующий результат:
decision tree Ветер ['Есть:6', 'Нет:8']
Гольф=?
Погода=ясно
Температура=Жарко
Влажность=Высокая['Есть:1', 'Нет:1']
Температура=Тепло['Нет:1']
Погода=Дождь['Есть:2']
Гольф=0
Погода=ясно
Температура=Тепло['Есть:1']
Температура=Холодно['Нет:1']
Погода=облачно
Температура=Жарко['Нет:2']
Температура=Тепло['Есть:1']
Температура=Холодно['Есть:1']
Погода=Дождь['Нет:3']По сути, мы создаем правило, при котором сообщаем программе, что разветвляться нужно сначала по наличию и отсутствию ветра и по тому, идем играть в гольф или нет.
Спасибо за прочтение!
Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?


rezdm
Пролог на питоне?
a-talentex Автор
Да, весь код в статье на питоне!
Xobotun
Нет, комментатор выше имел в виду "пролог" не как "начало статьи", а как "язык программирования высокого уровня". Я Пролог только в институте проходил, но описанное в статье очень сильно напоминает программы на Прологе.
Спасибо за перевод с японского, это было неожиданно. :)
a-talentex Автор
О, спасибо, что поправили, не понял вопроса :)
Вам спасибо за интерес!
Надеюсь, следующие публикации будут не менее интересными для вас :)