Имитация показаний датчиков с помощью массива точек пути / forpes.ru

Главная
Имитация показаний датчиков с помощью массива точек пути

Имитация показаний датчиков с помощью массива точек пути +30

11.04.2015 15:11

1div0 4 14091 Источник

Структура публикации

Оговорка про крен
Подготовка GPS-трека
Как из массива векторов получить углы Крылова-Эйлера
Имитация показаний гироскопа
Вектор ускорения свободного падения и направление «на север»
Имитация показаний акселерометра, компаса и барометра

Для отладки алгоритма, работающего с датчиками инерциальной навигации, может потребоваться имитировать показания этих самых датчиков. Например, вы имеете отладочную последовательность точек пути, имитирующую определённую ситуацию. Вы можете иметь некий GPS-трек, имеющий особенности, или напротив их не имеющий. В моём случае результат полевых испытаний есть, а плата ещё не готова (в производстве) — нужно чем-то заняться.

Оговорка про крен

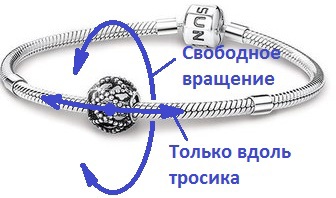
Стоит сразу отметить, что перемещаясь, 3D точка не даёт нам информации о положении тела относительно оси перемещения. Если представить, что между точками пути натянута нитка, а наш объект — это бусинка, то вдоль нитки она будет двигаться чётко, а вокруг оси движения может свободно вращаться. В качестве направления движения будем использовать вектор скорости и будем помнить оговорку про крен в результате.

Подготовка GPS-трека

Если у вас в качестве исходных данных GPS-трек, то нужно его сначала подготовить. Требуется преобразовать имеющийся файл к формату, из которого можно получить данные. Я преобразовывал к GPX (так как внутри это XML).

<trkpt lat="12.345678" lon="87.654321">
  <ele>839</ele>
  <time>2013-05-09T11:24:28.776Z</time>
  <extensions>
    <mytracks c="194.9" s="9.25" />
  </extensions>
</trkpt>
. . .
<trkpt lat="12.345678" lon="87.654321">
  <ele>837</ele>
  <time>2013-05-09T11:24:31.779Z</time>
  <extensions>
    <mytracks c="195.7" s="8.68" />
  </extensions>
</trkpt>

Далее берём любую доступную БД (например MySQL), создаём табличку и заполняем её данными из полученного XML. Формат XML может отличаться — главное найти широту, долготу, высоту и время. Создаём первую табличку, например 'xml_src'. Все столбцы для простоты загрузки делаем строковыми.

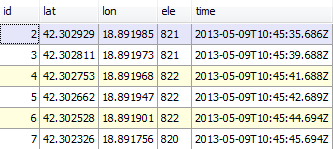
Немного причешем данные. Для удобства создадим вторую табличку, например 'points'. Код для MySQL:

insert into points (lat,lon,h,dt)
SELECT cast(xx.lat AS DECIMAL(11, 6)) 
     , cast(xx.lon AS DECIMAL(11, 6)) 
     , cast(xx.ele AS DECIMAL(11, 6)) 
     , cast(replace(replace(xx.`time`, "T", " "), "Z", "") AS DATETIME)
FROM
  xml_src AS xx;

В результате имеем следующее:

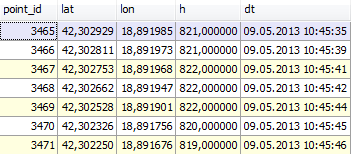
Затем переводим широту и долготу в метры (см. статью «Занимательная геодезия» или используем средства БД, например в MSSQL см. метод ShortestLineTo). Конвертировать в метры можно следующим образом. Мы считаем что координаты первой точки равны X = 0, Y = 0. Координаты каждой последующей точки считаем относительно первой. Определяем расстояние между точками сначала по вертикали, затем по горизонтали в метрах. Функция для рассчёта растояния есть в статье «Определение расстояния между географическими точками в MySQL».

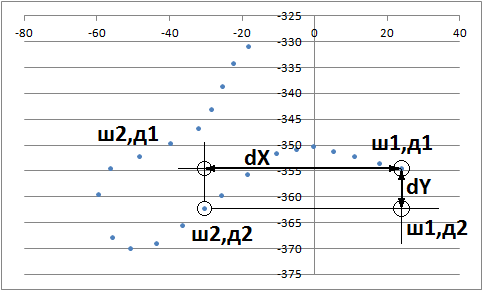
Время переводим в секунды так, чтобы в первой строке получилось 0 секунд (просто вычитаем значение первой строки из остальных).

Запрос для MySQL

Для удобства создадим третью табличку 'track' и функцию 'geodist' по координатам двух точек возвращающая расстояние в метрах.

FUNCTION geodist(src_lat DECIMAL(9, 6),
                        src_lon DECIMAL(9, 6),
                        dst_lat DECIMAL(9, 6),
                        dst_lon DECIMAL(9, 6)
                        )
  RETURNS decimal(11,3)
  DETERMINISTIC
BEGIN
  SET @dist := 6371000 * 2 * asin(sqrt(
  power(sin((src_lat - abs(dst_lat)) * pi() / 180 / 2), 2) +
  cos(src_lat * pi() / 180) *
  cos(abs(dst_lat) * pi() / 180) *
  power(sin((src_lon - dst_lon) * pi() / 180 / 2), 2)
  ));
  RETURN @dist;
END

Затем выберем начальную точку и используем её координаты в запросе. Мы будем мерить расстояние от этой точки до каждой следующей по вертикали и горизонтали в метрах.

INSERT INTO track (x, y, z, dt)
SELECT if(42.302929 > pp.lat, 1, -1) * geodist(42.302929, 18.891985, pp.lat, 18.891985)
     , if(18.891985 > pp.lon, -1, 1) * geodist(42.302929, 18.891985, 42.302929, pp.lon)
     , h
     , dt
FROM
  points AS pp;

В результате имеем следующее:

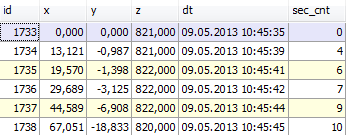
Теперь нам нужно получить координаты точки в равные промежутки времени. То, что вторая точка появились через 4 секунды после первой, третья через 2 секунды, а следующая через секунду – нас так не устраивает. Мы же собираемся имитировать датчики? А они измеряют значения в равные промежутки времени.

Для получения координат точки в равные промежутки времени используем интерполяцию. В качестве инструмента интерполяции используем одномерный кубический сплайн. У меня под рукой был Excel, я в нём макрос написал (см. спойлер). На этом этапе мы решаем с какой частотой будет работать каждый «датчик». Например, все «датчики» будут давать значения 10 раз в секунду. То есть интервал между измерениями равен 0,1 секунды.

Кубический сплайн на VB

Public Sub interpolate()

'------------------------
Dim i As Integer

Const start_n As Integer = 0
Const n As Integer = 1718

Dim src_x(n) As Double
Dim src_y(n) As Double
Dim spline_x(n) As Double
Dim spline_a(n) As Double
Dim spline_b(n) As Double
Dim spline_c(n) As Double
Dim spline_d(n) As Double

For i = start_n To n - 1
    spline_x(i) = Application.ActiveWorkbook.ActiveSheet.Cells(i + 1, 1).Value
    spline_a(i) = Application.ActiveWorkbook.ActiveSheet.Cells(i + 1, 2).Value
    src_x(i) = spline_x(i)
    src_y(i) = spline_a(i)
Next

spline_c(0) = 0

Dim alpha(n - 1) As Double
Dim beta(n - 1) As Double
Dim a As Double
Dim b As Double
Dim c As Double
Dim F As Double
Dim h_i As Double
Dim h_i1 As Double
Dim z As Double
Dim x As Double

alpha(0) = 0
beta(0) = 0

For i = start_n + 1 To n - 2
    h_i = src_x(i) - src_x(i - 1)
    h_i1 = src_x(i + 1) - src_x(i)
    If (h_i = 0) Or (h_i1 = 0) Then
        MsgBox ("ОШИБКА! Строка " + CStr(i + 1) + " Нет изменения по координате X! Это одномерный сплайн!")
        Exit Sub
    End If
    a = h_i
    c = 2 * (h_i + h_i1)
    b = h_i1
    F = 6 * ((src_y(i + 1) - src_y(i)) / h_i1 - (src_y(i) - src_y(i - 1)) / h_i)
    z = (a * alpha(i - 1) + c)
    alpha(i) = -b / z
    beta(i) = (F - a * beta(i - 1)) / z
Next

spline_c(n - 1) = (F - a * beta(n - 2)) / (c + a * alpha(n - 2))
For i = n - 2 To start_n + 1 Step -1
    spline_c(i) = alpha(i) * spline_c(i + 1) + beta(i)
Next

For i = n - 1 To start_n + 1 Step -1
    h_i = src_x(i) - src_x(i - 1)
    spline_d(i) = (spline_c(i) - spline_c(i - 1)) / h_i
    spline_b(i) = h_i * (2 * spline_c(i) + spline_c(i - 1)) / 6 + (src_y(i) - src_y(i - 1)) / h_i
Next

'-------------------------------
' my

Dim dx As Double
Dim j As Integer
Dim k As Integer
Dim y As Double
row_num = 1

For x = 0 To 3814 Step 0.1
    i = 0
    j = n - 1
    Do While i + 1 < j
        k = i + (j - i) / 2
        If x <= spline_x(k) Then
            j = k
        Else
            i = k
        End If
    Loop
    
    dx = x - spline_x(j)
    y = spline_a(j) + (spline_b(j) + (spline_c(j) / 2 + spline_d(j) * dx / 6) * dx) * dx
    Application.ActiveWorkbook.ActiveSheet.Cells(row_num, 3).Value = x
    Application.ActiveWorkbook.ActiveSheet.Cells(row_num, 4).Value = y
    row_num = row_num + 1
Next

End Sub

Интерполируем парами:

Время – X
Время – Y
Время – Z

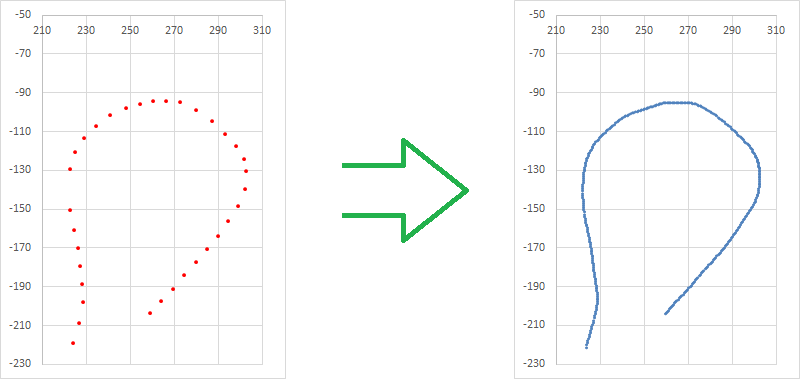
В итоге получается таблица с координатами точек «объекта», в котором находятся наши «датчики». Временной интервал между точками составляет 0,1 секунды. Время появления координат конкретной точки вычисляется по формуле t = n / 10, где n — это номер строки.

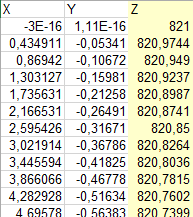
Как из массива векторов получить углы Крылова-Эйлера

Возьмём перемещение носа самолёта из моей предыдущей статьи:

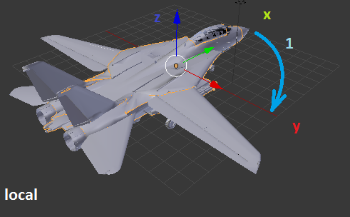
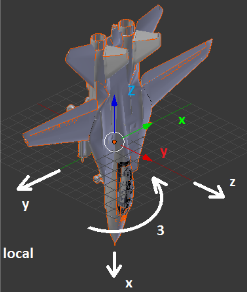
Координаты точки, означающей нос равны:

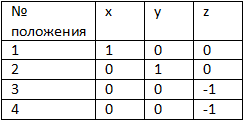
Давайте определим все три поворота. Для этого получим ось первого вращения v и угол первого поворота alf вокруг оси. Пусть точки пути – это вершины векторов. Тогда ось получим путём умножения соседних векторов.

v12 = v1 * v2 = (1; 0; 0) * (0; 1; 0) = (0; 0; 1)

Угол вычисляется следующим образом:

Public Function vectors_angle(v1 As TVector, v2 As TVector) As Double
    v1 = normal(v1)
    v2 = normal(v2)
    vectors_angle = Application.WorksheetFunction.Acos(v1.x * v2.x + v1.y * v2.y + v1.z * v2.z)
End Function

Alf12 = 90. Теперь создаём кватернион на основе полученных осей и углов:

Public Function create_quat(rotate_vector As TVector, rotate_angle As Double) As TQuat
    rotate_vector = normal(rotate_vector)
    create_quat.w = Cos(rotate_angle / 2)
    create_quat.x = rotate_vector.x * Sin(rotate_angle / 2)
    create_quat.y = rotate_vector.y * Sin(rotate_angle / 2)
    create_quat.z = rotate_vector.z * Sin(rotate_angle / 2)
End Function

Получаем первый кватернион:

(w=0,7071; x=0; y=0; z=0,7071)

Из кватерниона получим компоненты поворота:

    sqw = w * w
    sqx = x * x
    sqy = y * y
    sqz = z * z
    
    bank = atan2(2 * (w * x + y * z), 1 - 2 * (sqx + sqy))
    altitude = Application.WorksheetFunction.Asin(2 * (w * y - x * z))
    heading = atan2(2 * (w * z + x * y), 1 - 2 * (sqy + sqz))

Результат определения первого поворота: курс = 90, тангаж = 0, крен = 0.

Остальные повороты мы так посчитать не можем, так как после первого поворота локальная система координат самолёта перестала совпадать с глобальной системой координат. Для определения второго поворота от положения носа самолёта №2 к положению №3 нужно сначала отменить первый поворот, то есть вернуть систему отчёта на место и вместе с ней развернуть новый результирующий вектор. Для этого требуется получить обратный кватернион первого разворота и применить его на векторы №2 и №3 (получение обратного кватерниона и поворот вектора кватернионом – см. в статье).
Обратный кватернион первого разворота (поворот против часовой вдоль оси Z):

(w=0,7071; x=0; y=0; z=-0,7071)

После применения данного кватерниона второй и третий векторы равны:
v2 = (x=1; y=0; z=0)
v3 = (x=0; y=0; z=-1)

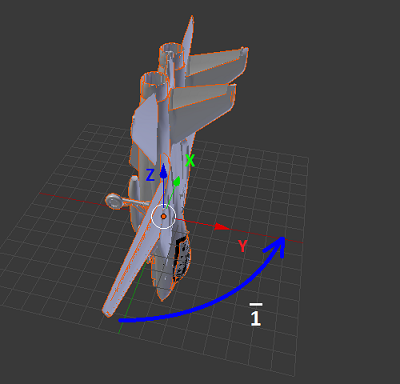
Когда локальная система координат совмещена с глобальной, можно вышеописанным способом вычислить второй кватернион и компоненты второго поворота:

(w=0,7071; x=0; y=0; z=-0,7071),
курс = 0, тангаж = 90, крен = 0.

Дальше мы должны запоминать совершённые развороты в локальной системе координат. Для этого заведём отдельный кватернион и в него будем умножать кватернионы поворотов:

Затем из кватерниона серии совершённых разворотов будем получать обратный кватернион для совмещения систем отчёта.

Подведём итог. Чтобы получить компоненты поворотов по списку векторов, обозначающих направление движения, требуется выполнить следующее:

' кватернион "нет поворота"
q_mul.w = 1
q_mul.x = 0
q_mul.y = 0
q_mul.z = 0

For row_n = M To N
    
' текущее положение поворачиваемого вектора
    v1.x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 1).Value
    v1.y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 2).Value
    v1.z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 3).Value

' следующее целевое положение вектора
    v2.x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    v2.y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    v2.z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value

' совмещаем системы отчёта для чего разворачиваем векторы     
    q_inv = myMath.quat_invert(q_mul) ' получение обратного кватерниона
    v1 = myMath.quat_transform_vector(q_inv, v1) ' разворот вектора кватернионом
                                         ' в этом примере для всех шагов получим (length(v1); 0; 0) – его исходное положение
    v2 = myMath.quat_transform_vector(q_inv, v2) ' разворот вектора кватернионом
    
' ищем кватернион нового разворота
    r12 = myMath.vecmul(v1, v2) ' умножение векторов
    alf = myMath.vectors_angle(v1, v2) ' получаем угол между векторами
    q12 = myMath.create_quat(r12, alf) ' создаём кватернион на основе оси и угла разворота
        
' получаем компоненты углов
    ypr = myMath.quat_to_krylov(q12)
    
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 4).Value = ypr.heading
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 5).Value = ypr.altitude
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 6).Value = ypr.bank
  
' добавляем поворот в серию
    q_mul = myMath.quat_mul_quat(q_mul, q12) ' умножение кватернионов
    
Next

В данном макросе для Excel-я векторы считываются с первых трёх столбиков. Результат пишется в 4, 5, 6 столбик.

Имитация показаний гироскопа

Как вы понимаете, координаты точек в качестве входных данных не годятся — нам нужны векторы скорости.

Получить скорость и ускорение из подготовленных данных легко – разница между соседними строчками таблицы координат точек – это скорость, разница между соседними строчками скорости – это ускорение. Только нужно помнить про частоту замеров. В данном случае у нас 10 «измерений» в секунду. Это значит, чтобы получить, например, скорость в метрах в секунду, нужно значение соответствующей ячейки умножить на 10.

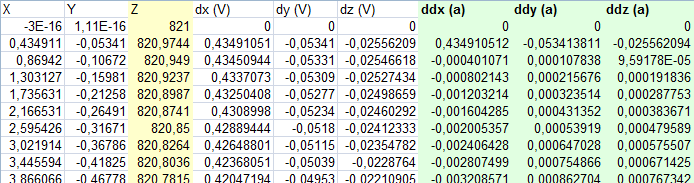
Берём векторы скорости и получаем компоненты поворота.

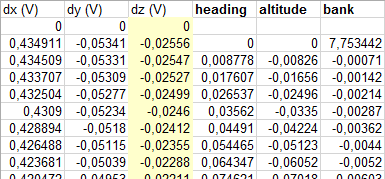
Теперь про гироскоп. Гироскоп показывает угловую скорость. Наши компоненты поворотов в локальной системе координат в равные промежутки времени — это и есть угловая скорость.

Кроме получения угловой скорости, нужно ещё прибавить шум. В шуме гироскопа присутствует два ощутимых компонента — собственный шум датчика (равномерное распределение) и влияние вращения земли (если ваш «датчик» не в космосе). Уровень собственного шума датчика описан в спецификации (изучаем datasheet на имитируемый датчик). Мой датчик имеет разрешение 16 бит и имеет 4 режима измерения. У каждого режима свой максимум: у первого ±250?/сек,… у четвёртого ±2000?/сек. Чувствительность для первого режима 131 LSB/(?/s). Чтобы посчитать это в градусах, нужно воспользоваться формулой:

Чувствительность = Чувствительность_LSB * Максимум / Разрешение = 131 * ±250 / (2 ^ 16) = 131 * ±250 / 65536 = ±0,49972534 ?/сек.

То есть величина шума в пределах одного градуса. Формула для Excel-я:
=(СЛЧИС()-0,5)/N, где N — это число имитируемых «измерений» в секунду.

Земля вращается со скоростью 15 градусов в час. Это 0,0041667 градусов в секунду, что сильно меньше погрешности измерения. Забавы ради можно рассчитать и это.

Предположим, что ось вращения Земли совпадает с осью Z. Предположим также, что тело находится на экваторе и ось Y тела ориентировано строго на север (по касательной). Тогда ось Х тела совпадает с касательной направления вращения. В этом случае ось вращения Земли и тела вместе с ним совпадает с осью Z тела. Зрительно представим смещение по широте нашего тела к северу. Тогда ось вращения повернётся вокруг оси Х по часовой стрелке на число градусов, равное значению новой широты. При смещении в северное полушарие — это знак плюс, в южное — знак минус. Когда тело свободно ориентировано в пространстве, нам поможет вектор ускорения свободного падения — g.

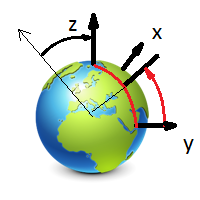
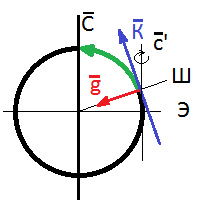
Для вычисления оси вращения Земли в локальной системе координат нужно:

Умножить вектор g на вектор показания компаса «на север».
Создать кватернион на основе получившегося вектора и угла. В качестве значения угла берём широту.
Развернуть получившимся кватернионом вектор компаса «на север».

Для получения значений разворота нашего тела планетой в момент каждого замера делаем:

Вычисляем вектор оси вращения планеты используя текущую широту из исходных данных.
Вычисляем на сколько повернулась планета с момента последнего измерения. В нашем случае при измерении 10 раз в секунду это будет 0,0041667 / 10 = 0,00041667.
Строим кватернион на основе вектора оси и угла разворота.
Получаем три компоненты разворота (курс, тангаж, крен) и прибавляем к показаниям «датчика».

В общем в итоге всего получим таблицу:

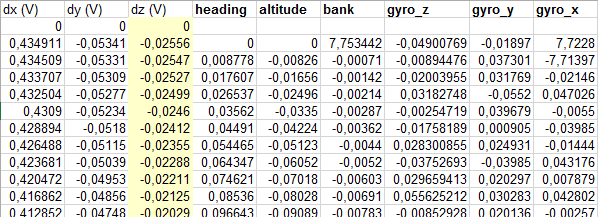
Последние три столбца — это «показания гироскопа».

Вектор ускорения свободного падения и направление «на север»

Предположим, что есть единичный вектор С, который совпадает с касательной к меридиану и направлением «юг» -> «север». Пусть ось Y нашей глобальной системы координат совпадает с вектором С = (0, 1, 0). А вектор ускорения свободного падения g направлен вдоль оси Z, но в противоположную сторону. g = (0, 0, -1). Тогда, если явно указать вектор скорости тела в начальный момент времени как Н = (1, 0, 0), то все развороты, полученные на основе вращений вектора скорости будут применимы и для вращений векторов g и С. Вращать эти векторы нужно обратным кватернионом. Обратный от кватерниона, который накапливает все совершённые повороты вектора скорости (q_mul).

Достаточно добавить пару строк в процедуру расчёта углов поворота. Теперь она выглядит так:

Public Sub calc_all()

Dim v1 As myMath.TVector
Dim v2 As myMath.TVector
Dim r12 As myMath.TVector
Dim m12 As myMath.TMatrix
Dim q12 As myMath.TQuat
Dim q_mul As myMath.TQuat
Dim q_inv As myMath.TQuat
Dim ypr As myMath.TKrylov
Dim alf As Double
Dim row_n As Long
Dim g As myMath.TVector
Dim nord As myMath.TVector

q_mul.w = 1
q_mul.x = 0
q_mul.y = 0
q_mul.z = 0

For row_n = 3 To 38142
    
    v1.x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 1).Value
    v1.y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 2).Value
    v1.z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 3).Value
    v2.x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    v2.y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    v2.z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
    g.x = 0
    g.y = 0
    g.z = -1
    nord.x = 0
    nord.y = 1
    nord.z = 0
    
    q_inv = myMath.quat_invert(q_mul)
    v1 = myMath.quat_transform_vector(q_inv, v1)
    v2 = myMath.quat_transform_vector(q_inv, v2)
    g = myMath.quat_transform_vector(q_inv, g)
    nord = myMath.quat_transform_vector(q_inv, nord)
    
    r12 = myMath.vecmul(v1, v2)
    alf = myMath.vectors_angle(v1, v2)
    q12 = myMath.create_quat(r12, alf)
    ypr = myMath.quat_to_krylov(q12)
    
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 4).Value = ypr.heading
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 5).Value = ypr.altitude
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 6).Value = ypr.bank
    
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 7).Value = g.x
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 8).Value = g.y
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 9).Value = g.z
    
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 10).Value = nord.x
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 11).Value = nord.y
    Application.ActiveWorkbook.ActiveSheet.Cells(row_n - 1, 12).Value = nord.z
    
    q_mul = myMath.quat_mul_quat(q_mul, q12)
    
Next

End Sub

Первые три столбца — вектор скорости, с явно указанным направлением в первой точке. Это входные данные. Затем три столбца — расчётные углы поворота. Далее вектор направления «на север» и вектор ускорения свободного падения. И наконец три столбика — это имитируемые показания гироскопа.

Имитация показаний акселерометра, компаса и барометра

Так как у нас всё движение происходит вдоль вектора скорости, то и ускорение у нас направлено так же вдоль вектора скорости — это значит вдоль оси X. Показания датчика ускорения складываются из трёх ощутимых компонентов: ускорение свободного падения, шумы и собственно ускорение тела:

a = (x = length(a), 0, 0);
A = a + (9,8 / N) * g + rnd,
где a — расчётный по входным данным вектор ускорения,
N — количество имитируемых измерений в секунду,
g — вектор ускорения свободного падения,
rnd — шум.
Величина шума снова зависит от имитируемого датчика. Для расчёта смотрим в спецификацию и используем ту же формулу:

Чувствительность = Чувствительность_LSB * Максимум / Разрешение = 16,384 * ±2 / 65536 = ±0,0005 g = ±0,0049 м/с2.

Тогда можно немножко ухудшить результат и выразить имитируемые показания датчика ускорения простыми формулами:
Ax = length(a) + gx * 9,8 / N + random(0,01) — 0,005
Ay = gy * 9,8 / N + random(0,01) — 0,005
Az = gz * 9,8 / N + random(0,01) — 0,005

Диапазон измерений компаса в спецификациях дают в Теслах. Магнитное поле Земли будет на уровне 0,00005 T = 50 uT. Посчитаем чувствительность по той же формуле:

Чувствительность = 15uT * ±4800uT / 65536 = ±1uT.

Это даёт разброс в пределах 4%. Поскольку показания компаса так или иначе приводятся к вектору «на север», то в качестве показаний компаса можно просто взять уже рассчитанный вектор и «ухудшить» каждую его составляющую на 4%:
mx = Cx + random(2) — 1
my = Cy + random(2) — 1
mz = Cz + random(2) — 1.

С барометром всё ещё проще. Их показания приводятся к высоте в метрах, разброс обычно в пределах метра (см. спецификацию, бывает меньше). Если нужны прям показания датчика в Па — см. барометрическую формулу. А так

h = Z + random(1) — 0,5.

Вот собственно и всё. Кому понравилось — не забывайте ставить плюсики. Если хотите статью на тему обратной задачи (от датчиков к точкам пути) — пишите в комментариях.

Комментарии (4)

martsen
11.04.2015 19:44
#8372711
+1
Спасибо за материал! Статью про обратную задачу обязательно публикуйте.

Moskus
11.04.2015 19:45
#8372715
+1
То, что делается в самом начале (преобразование GPX в таблицу и пересчет из географических координат в декартовы) можно сделать несколько проще.
Есть такой широко применяемый конвертер — GPSBabel, среди поддерживаемых им форматов есть так называемый Universal CSV. Можно проделать через него только преобразование из GPX в текстовую таблицу, а можно, повозившись с параметрами, заставить его выдать координаты уже в системе UTM, то есть в метрах, в декартовых координатах.
Другой вариант — использовать более профессиональное средство — утилиты GDAL/OGR. Они тоже поддерживают GPX на чтение, а сохранять могут CSV в разных системах координат (и там это несколько более документировано).

Ну и давайте все же писать по-русски, слово «вектор» во множественном числе именительного падежа звучит как «векторы».

utya
13.04.2015 21:58
#8374521
Круто. Спасибо.

xtile
27.04.2015 20:15
#8395715
Добрый день!

Как с вами можно связаться?

Возможно, у меня для вас будет деловое предложение по тематике статьи

Имитация показаний датчиков с помощью массива точек пути +30

Структура публикации

Оговорка про крен

Подготовка GPS-трека

Как из массива векторов получить углы Крылова-Эйлера

Имитация показаний гироскопа

Вектор ускорения свободного падения и направление «на север»

Имитация показаний акселерометра, компаса и барометра

Комментарии (4)

martsen

Moskus

utya

xtile